Задание 23 из ОГЭ по математике

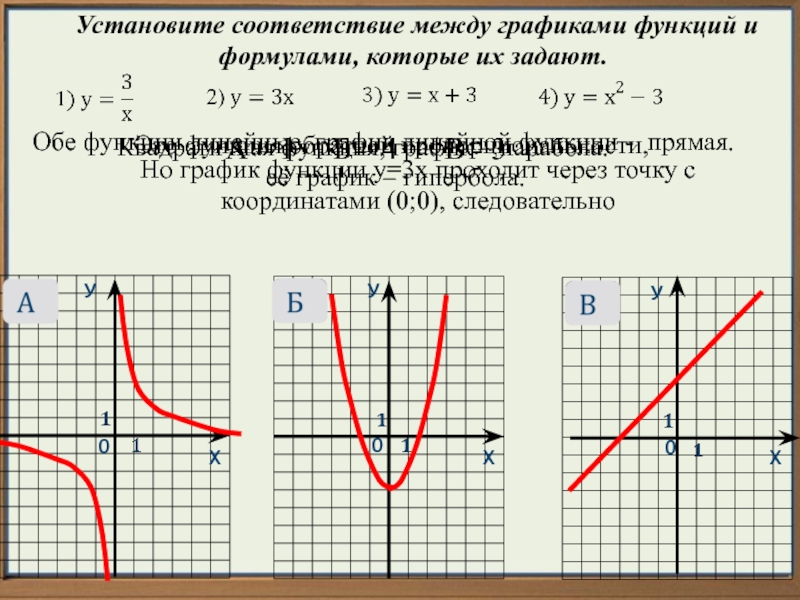
задают.
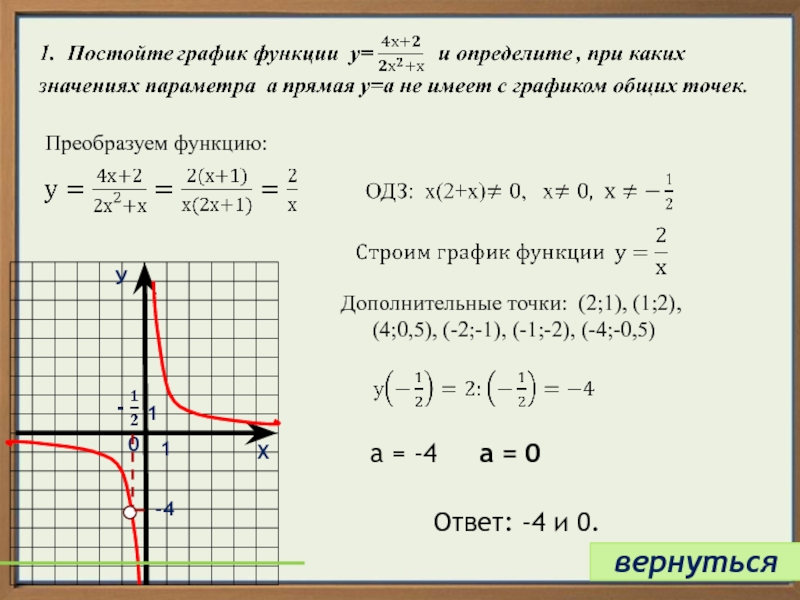
Это функция обратной пропорциональности,
её график – гипербола.
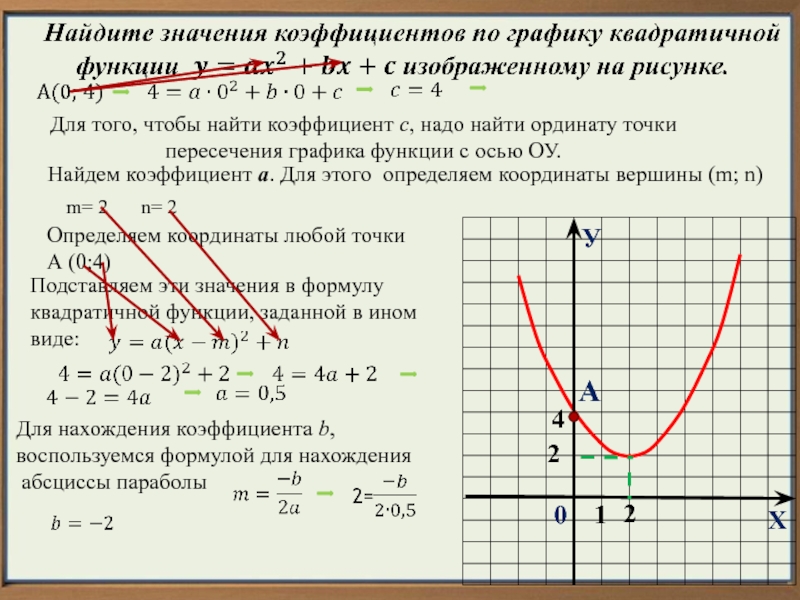
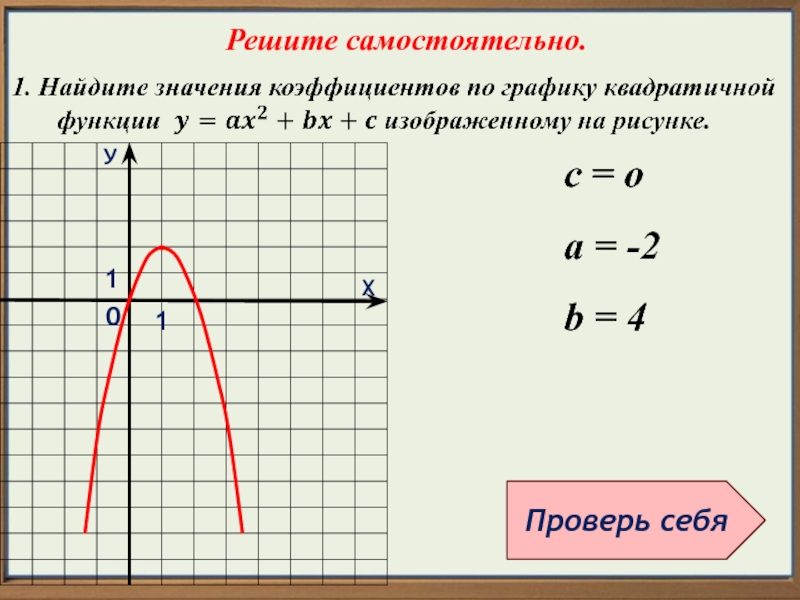
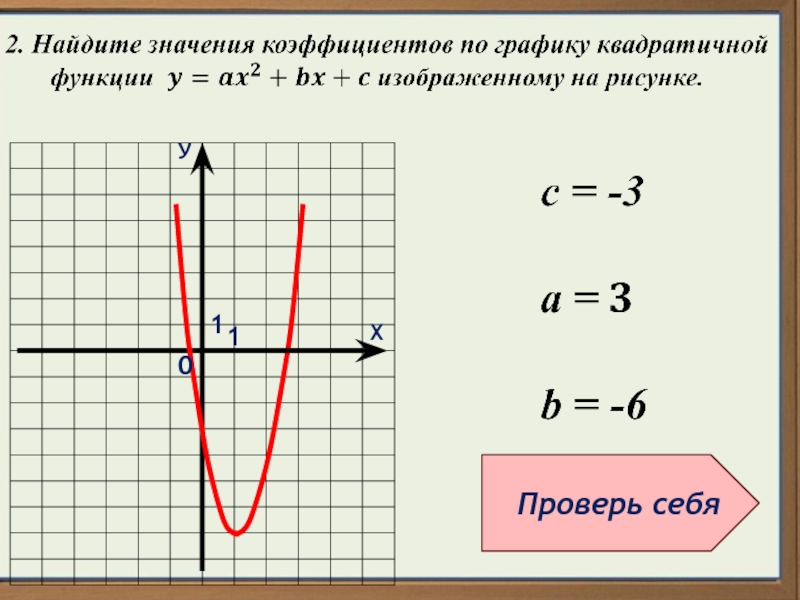
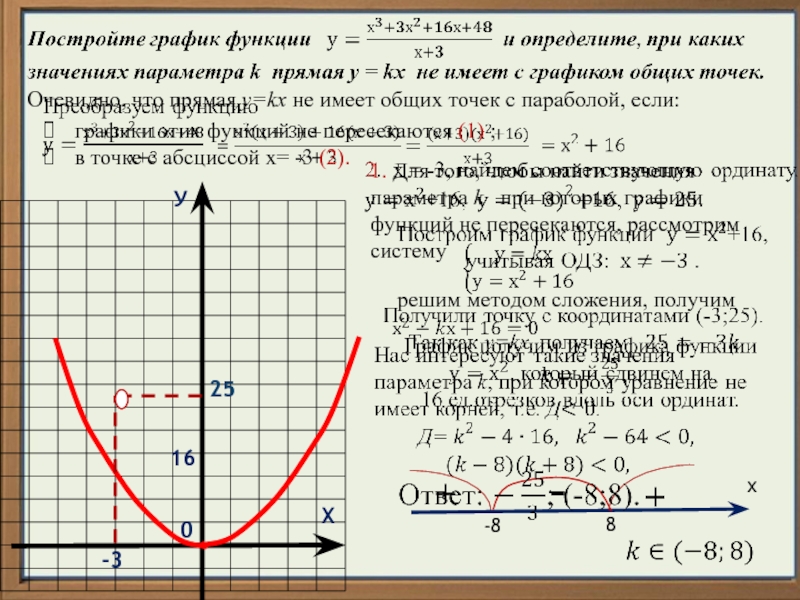
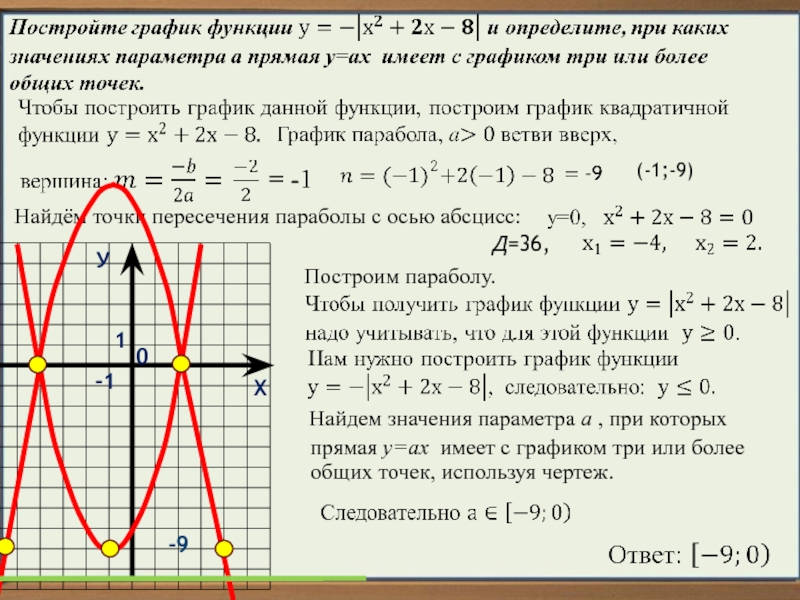
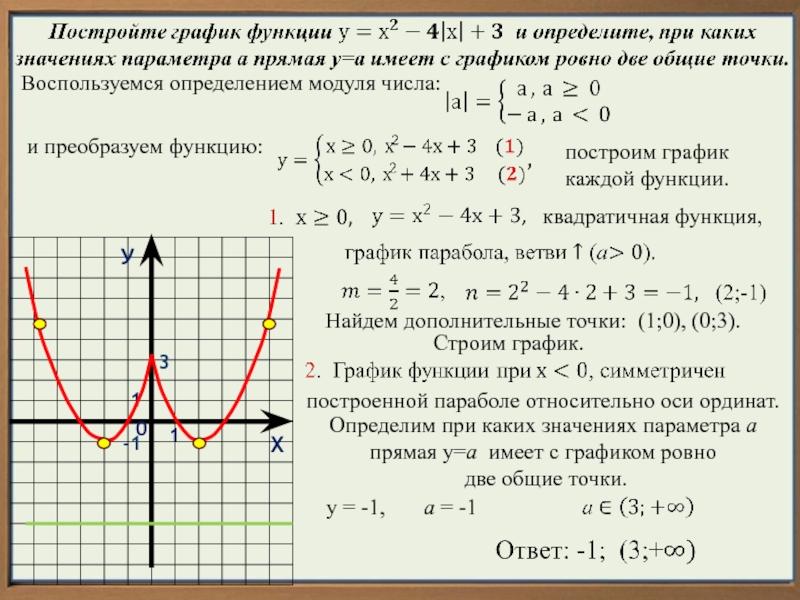
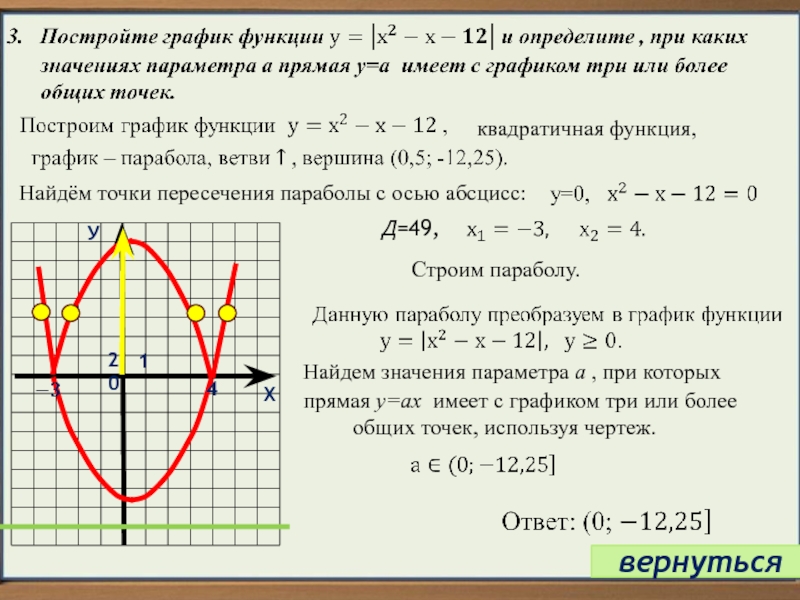
Квадратичная функция, график

Но график функции у=3х проходит через точку с
координатами (0;0), следовательно

Обе функции линейные, график линейной функции - прямая.

А – 1 Б – 4 В - 3

точки, принадлежащей графику функции.
2
А
Очевидно, что точка А(1;2) принадлежит функции №3.

как в предыдущей задаче.
-2
2
А – 1 Б –

задают.
Проверь себя

точки пересечения графика функции с осью ОУ.
Найдем коэффициент а. Для

2

m= 2

n= 2

Определяем координаты любой точки
А (0;4)

Подставляем эти значения в формулу квадратичной функции, заданной в ином виде:
 

Для нахождения коэффициента b,
воспользуемся формулой для нахождения
абсциссы параболы

не имеет с графиком общих точек.
у = а
- 1,5
а =

а = 0

Ответ: 0 и – 1,5.

а = -1,5

если:
графики этих функций не пересекаются (1) ;
в точке

1. Для того, чтобы найти значения параметра k при которых графики функций не пересекаются, рассмотрим систему

решим методом сложения, получим

8

-8

х

+

-

+

абсцисс:
Д=36,
Построим параболу.
Найдем значения параметра а

прямая у=ах имеет с графиком три или более

общих точек, используя чертеж.

каждой функции.
квадратичная функция,
Найдем дополнительные точки: (1;0), (0;3).
Строим график.
построенной

Определим при каких значениях параметра а
прямая у=а имеет с графиком ровно
две общие точки.

у = -1, а = -1

-1

3

= 0
-4
а = -4
Ответ: -4 и 0.
вернуться

(1;2), (2;4), (3;8).
Строим график функции (1).
построенной параболе относительно оси ординат.
Определим

1,75

а = -1,75

вернуться

Д=49,
Строим параболу.
4
Найдем значения параметра а , при

прямая у=ах имеет с графиком три или более

общих точек, используя чертеж.

вернуться

9,25 = 0,5 k; k=18,5
Для того, чтобы

при которых графики функций не пересекаются,

Х

6

-6

-

f(0)=-36

+

+

Ответ: 18,5 ; (-6;6).

вернуться