Арифметическая и геометрическая прогрессии.

области

Пройдена теории схема, Вы много новых формул узнали,

Задачи с прогрессией решали. И вот в последний урок Нас поведет Красивый лозунг “ПРОГРЕССИО - ВПЕРЕД”

81; 243;…
3) 1; 6; 11; 20; 25;…
4) –4; –8;

–16; –32; …
5) 5; 25; 35; 45; 55;…
6) –2; –4; – 6; – 8; …

арифметическая прогрессия d = 3

арифметическая прогрессия d = – 2

геометрическая прогрессия q = 3

последовательность чисел

геометрическая прогрессия q = 2

последовательность чисел

автором Боэцием еще в IV в. н.э. От латинского слова

progressio – “движение вперед”. Первые представления об арифметической прогрессии были еще у древних народов. В клинописных вавилонских табличках и египетских папирусах встречаются задачи на прогрессии и указания как их решать. Считалось, что в древнеегипетском папирусе Ахмеса находилась древнейшая задача на прогрессии о вознаграждении изобретателя шахмат, насчитывающая за собою двухтысячелетнюю давность. Но есть гораздо более старая задача о делении хлеба, которая записана в знаменитом египетском папирусе Ринда. Папирус этот, разысканный Риндом полвека назад, составлен около 2000 лет до нашей эры и является списком с другого, еще более древнего математического сочинения, относящегося, быть может, к третьему тысячелетию до нашей эры. В числе арифметических, алгебраических и геометрических задач этого документа имеется такая, которую мы приводим в вольной передаче.

5 людьми так, чтобы второй получил на столько же больше

первого, на сколько третий получил больше второго, четвертый больше третьего и пятый больше четвертого. Кроме того, двое первых получили в 7 раз меньше трех остальных. Сколько нужно дать каждому?

прогрессию. Пусть первый ее член x, разность y. Тогда:
а1–Доля

первого – x,
а2–Доля второго – x+y,
а3–Доля третьего – x+2y,
а4–Доля четвертого – x+3y,
а5–Доля пятого – x+4у.
На основании условия задачи составляем следующие 2 уравнения:

имеем:
Значит, хлеб должен быть разделен на

следующие части:

а1 = 5 d = 3
Найти:

а6 ; а10.
Решение: используя формулу а n = а 1+( n -1) d
а6 = а1 +5 d = 5+ 5 . 3 = 20
а10 = а1 +9 d = 5+ 9 . 3 = 32
Ответ: 20; 32

Решение

q = 3
Найти: b3 ; b5.

Решение: используя формулу b n = b1 q n-1
b3 =b1q2 = 5 . 32 =5 . 9=45
b5 =b1q4 = 5 . 34 =5 . 81=405
Ответ:45; 405.

Решение

а4 = 11 d = 2
Найти:

а1 .
Решение: используя формулу а n= а 1+ ( n – 1) d
а4 = а1 +3 d ; а1= а4 – 3 d =11 – 3 . 2 = 5
Ответ: 5.

Решение

q = 2
Найти: b1.
Решение: используя

формулу b n = b1 q n-1
b4 =b1q3 ; b1 = b4 : q3 =40:23 =40 :8=5

Ответ: 5.

Решение

арифметической прогрессии. Оно, скорее всего, занимательное. Нам дана “стайка девяти

чисел”
3, 5, 7, 9, 11, 13, 15,17, 19.
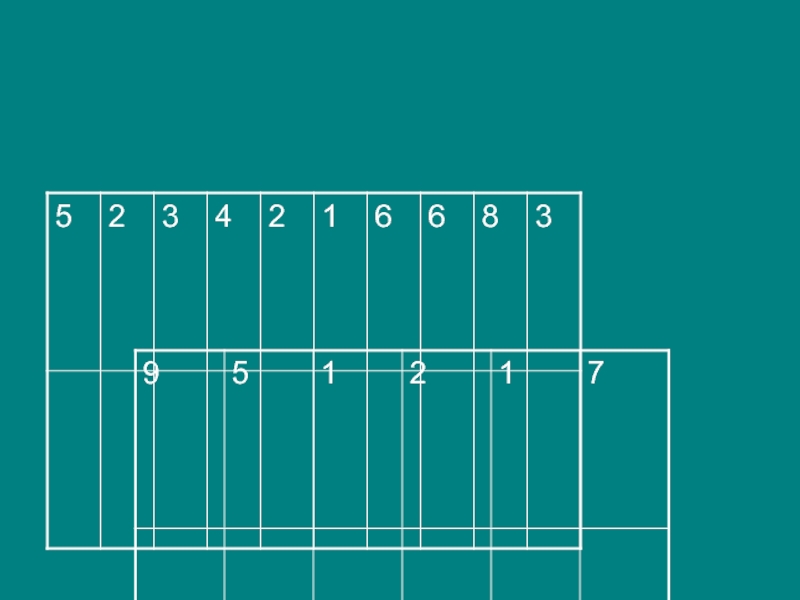
Она представляет собой арифметическую прогрессию. Кроме того, данная стайка чисел привлекательна способностью разместиться в девяти клетках квадрата так, что образуется магический квадрат с константой, равной 33

состоящий из 9 клеток, в него вписывают числа, так чтобы

сумма чисел по вертикали, горизонтали диагонали была одним и тем же числом – constanta.

Замечание об арифметической прогрессии само по себе очень интересно. Дело в том, что из каждых девяти последовательных членов любой арифметической прогрессии натуральных чисел можно составить магический квадрат.

константа C
которого равна 3a+12d.
Действительно, сумма

чисел в каждой строке,
в каждом столбце и по каждой диагонали квадрата равна 3a+12d.

Пусть дана арифметическая прогрессия: a, a+d, a+2d, a+3d, …, a+8d, где a и d натуральные числа. Расположим её члены в таблицу.

а6=17,5
Найти: а5
Решение: используя свойство
арифметической

прогрессии имеем:



Ответ: 15( О)

Решение

n >0
b4=6; b6=24
Найти: b5
Решение: используя

свойство
геометрической прогрессии имеем:





Ответ: 12( Д)

Решение

= – 3, а2 = 4.

Найти: а16 – ?
2)Дано: (b n ) , b 12 = – 32, b 13 = – 16.Найти: q – ?
3)Дано: (а n ), а21 = – 44, а22 = – 42. Найти: d - ?
4)Дано: (b n ) , bп > 0, b2 = 4, b4 = 9. Найти: b3 – ?
5)Дано: (а n ), а1 = 28, а21 = 4. Найти: d - ?
6) Дано: (b n ) , q = 2. Найти: b5 – ?
7) Дано: (а n ), а7 = 16, а9 = 30. Найти: а8 –?

1) ( П) ;2) ( В) ;3) ( Р); 4) ( Г); 5) ( Е); 6) ( С).

2) 0,5; ( В)

3) 2; ( Р)
4) 6; ( Г)
5) – 1,2; ( Е)
6) 8; ( С)

новой форме по алгебре в 9 классе, предлагаются задания которые

оцениваются в 2 балла:

6.1. 1) Пятый член арифметической прогрессии равен 8,4, а ее десятый член равен 14,4. Найдите пятнадцатый член этой прогрессии.
6.2. 1) Число –3,8 является восьмым членом арифметической прогрессии (ап), а число –11 является ее двенадцатым членом. Является ли членом этой прогрессии число –30,8?
6.5. 1) Между числами 6 и 17 вставьте четыре числа так, чтобы вместе с данными числами они образовали арифметическую прогрессию.
6.8. 1) В геометрической прогрессии b12 = З15 и b14 = З17. Найдите b1.

b1= –34).

упорство, труд
К прогрессу в жизни приведут.