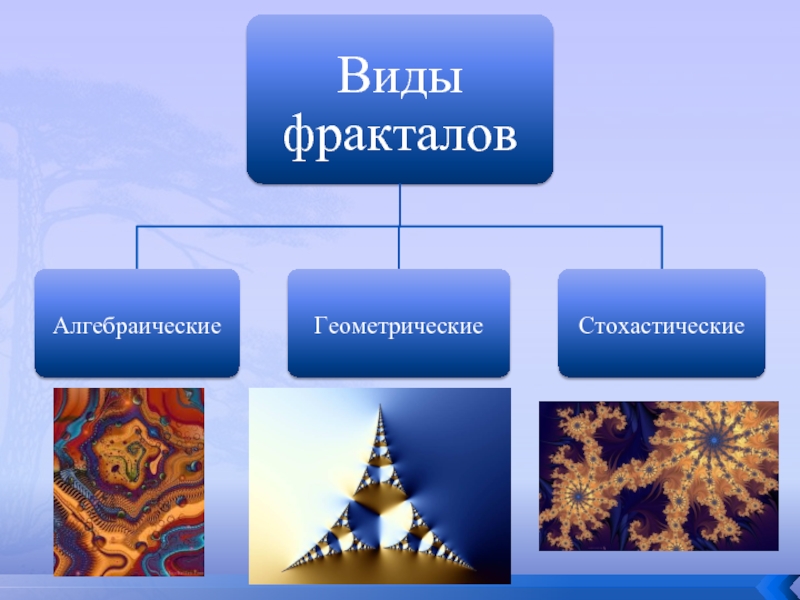
Жизнь фракталов

фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей,

каждая из которых подобна всей фигуре целиком.
Фрактал — это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба

получили, за то, что их строят, используя простые алгебраические формулы.

Получают их с помощью нелинейных процессов в n-мерных пространствах.
Самыми известными из них являются множества Мандельброта и Жюлиа, Бассейны Ньютона и т.д.

фракталов получается путем простых геометрических построений. Геометрические фракталы являются самыми

наглядными, т.к. геометрические фракталы обладают самоподобностью, не изменяющейся при изменении масштаба.

Треугольник Серпинского

параметры называются стохастичными. Термин "стохастичность" происходит от греческого слова, обозначающего

"предположение".
Эти фракталы используются при моделировании рельефов местности и поверхности морей, процесса электролиза.

для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение

фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта `The Fractal Geometry of Nature'. В его работах использованы научные результаты других ученых, работавших в период 1875-1925 годов в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф). Но только в наше время удалось объединить их работы в единую систему

Формула Мандельброта, объединяющая все множества Жюлиа в одно изображение.

F(z) = f2 + c

Варшаве в 1924 году в семье

литовских евреев. В 1936 году вся семья эмигрировала во Францию и поселилась в Париже.
В 1958 году Мандельброт поселился в США, где приступил к работе в научно-исследовательском центре IBM в Йорктауне, поскольку IBM в то время занималась интересными Бенуа Мандельброту областями математики.
Исследуя экономику, Мандельброт обнаружил, что произвольные внешне колебания цены могут следовать скрытому математическому порядку во времени, который не описывается стандартными кривыми.

применено американским инженером Натаном Коэном. Натан вырезал из алюминиевой фольги

фигуру в форме кривой Коха и наклеил её на лист бумаги, затем присоединил к приёмнику. Коэн основал собственную компанию и наладил их серийный выпуск.

Кривая коха

процессов, таких, как течение жидкости, пламя, облака и т. п.

Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).

природных объектов, таких, как деревья, кусты, горные ландшафты, поверхности морей

и так далее. Существует множество программ, служащих для генерации фрактальных изображений, для сжатия данных.

(и сейчас используют) фракталы в своём творчестве. Одним из них

был Кацусико Хокусай. Например, на его картине «Большая волна в Канагаве» гребни больших волн состоят из множества более мелких волн.

систему выяснили, что её участки можно представить в виде фракталов.

Далее, изучая различные участки, они выяснили, что здоровые кровеносные сети и раковые опухоли имеют разную фрактальную структуру. Это может помочь при выявлении раковых опухолей на ранней стадии.

и мультимедиа материалы и узнал, что же представляют собой фракталы,

на какие виды они делятся и где применяются. На основе изученного материала можно сделать вывод, что фракталы находят применение в различных сферах деятельности человека (информатика, живопись, радиотехника), а также в некоторых науках, а именно в физике, биологии, химии и, конечно, в математике. Но наиболее часто фракталы используются при описании природных объектов и некоторых процессов, а также при их моделировании.

Научные; Страна выпуска: США; Продолжительность: 53 минут; Режиссеры фильма: Бил

Джерси, Майкл Швартс)
http://ru.wikipedia.org/wiki/Фрактальная_геометрия_природы
http://ru.wikipedia.org/wiki/Фрактал#.D0.9F.D1.80.D0.B8.D0.BC.D0.B5.D0.BD.D0.B5.D0.BD.D0.B8.D0.B5
http://www.adamaz.ru/988-obuchenie.html
http://ru.wikipedia.org/wiki/Мандельброт,_Бенуа
http://worldart.my1.ru/index/geometricheskiefraktalyrisunki_na_peske/0-57
http://evrika.tsi.lv/index.php?name=site&sid=27
http://blog.kp.ua/users/xtsarx/post169108433/
http://www.mystery-queen.com/data_images/Облака/Облака-02.jpg
http://gizmod.ru/uploads/posts/2000/14370/image.jpg
http://rusproject.narod.ru/article/fractals.htm#geom
http://masters.donntu.edu.ua/2007/mech/majeed/library/article4.html
http://art.liim.ru/galleries_hz/hz14b/hz14b-4-052.html
http://www.shkaff.net/stati/687-fraktaly.html
http://www.liveinternet.ru/journalshowcomments.php?jpostid=95730186&journalid=3072922&go=prev&categ=1
http://worldart.my1.ru/index/geometricheskiefraktalyrisunki_na_peske/0-57
http://ru.wikipedia.org/wiki/Треугольник_Серпинского
http://www.onix-trade.net/forum/index.php?showtopic=88828