Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы счисления.
Содержание
- 1. Системы счисления.
- 2. Добрый день☺ Итак, сегодня мы проводим
- 3. Что будем делать?☺ Сегодня мы познакомимся
- 4. Давайте вместе ответим на вопросы:Система счисления –
- 5. А можно ли переводить числа из одной
- 6. перевод чисел из системы счисления с основанием
- 7. Перевод чисел из системы счисления с основанием
- 8. Для перевода двоичного числа в десятичное необходимо
- 9. Для перевода восьмеричного числа в десятичное необходимо
- 10. Для перевода шестнадцатеричного числа в десятичное необходимо
- 11. перевод чисел из системы счисления с основанием
- 12. Перевод чисел из десятичной системы счисления в
- 13. Это была скучная теория, теперь более веселая (и понятная) практика:
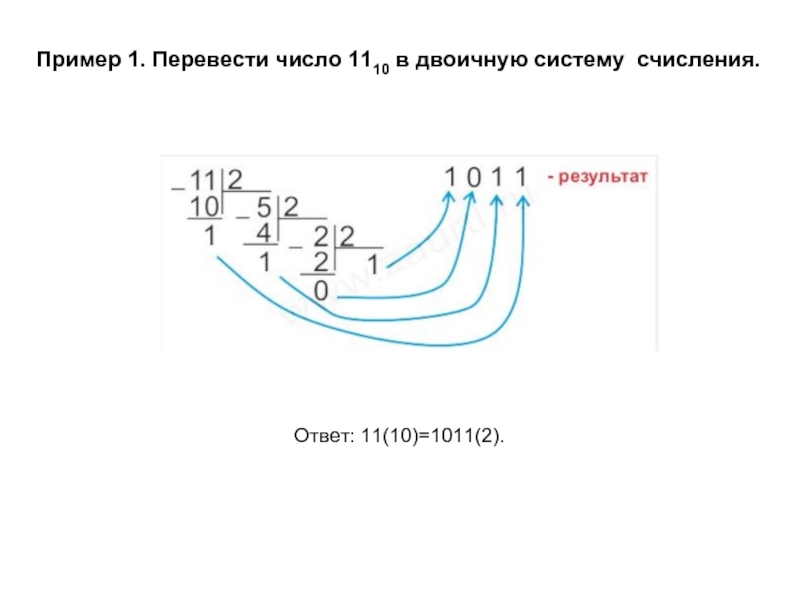
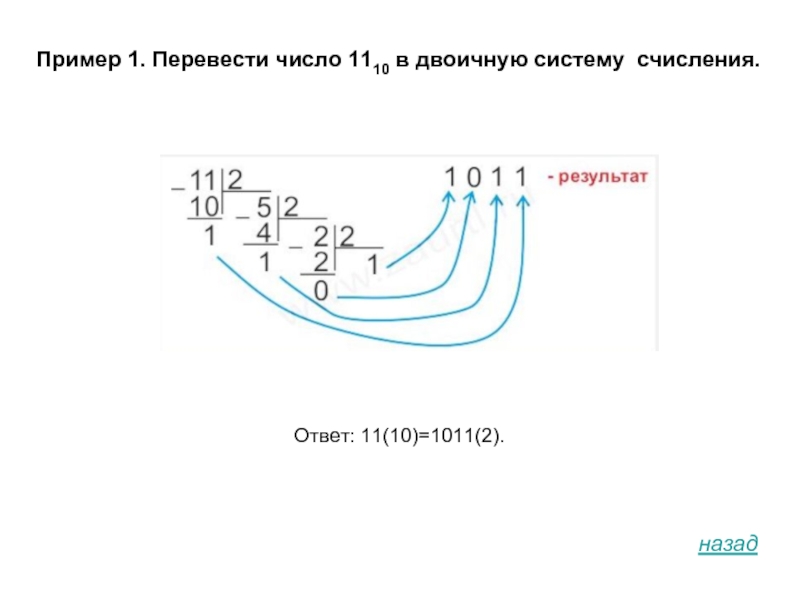
- 14. Пример 1. Перевести число 1110 в двоичную систему счисления. Ответ: 11(10)=1011(2).
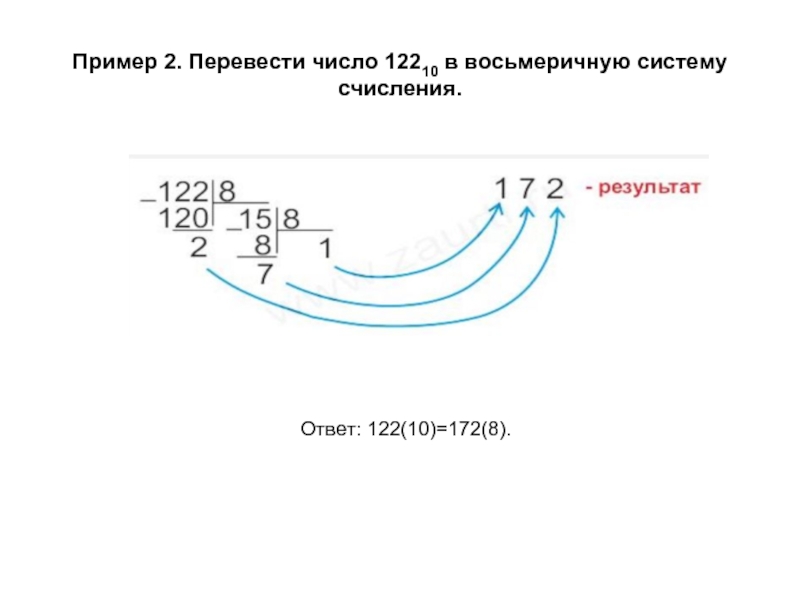
- 15. Пример 2. Перевести число 12210 в восьмеричную систему счисления.Ответ: 122(10)=172(8).
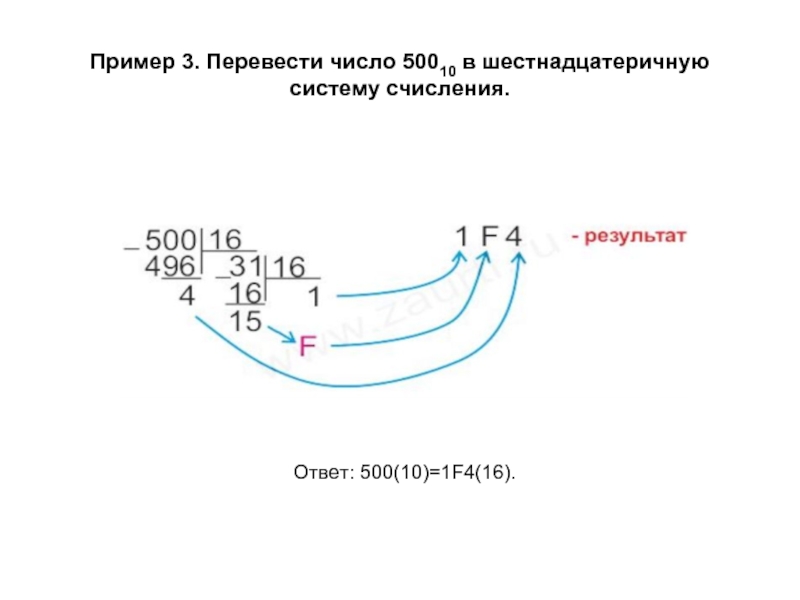
- 16. Пример 3. Перевести число 50010 в шестнадцатеричную систему счисления. Ответ: 500(10)=1F4(16).
- 17. Тренировочные упражненияПеревести числа из десятичной системы счисления
- 18. После того как произвели вычисления, давайте посмотрим как должно получиться
- 19. ОтветыПеревести числа из десятичной системы счисления в
- 20. Ответы2) Перевести числа в
- 21. Подведем итоги: Итак, сегодня мы познакомились
- 22. перевод чисел из системы счисления с основанием
- 23. Пример 1. Перевести число 1110 в двоичную систему счисления. Ответ: 11(10)=1011(2).назад
- 24. При переводе «вручную» чисел из одной системы счисления в другую, надо быть внимательным и терпеливым☺.
- 25. Домашнее заданиеПеревести числа из десятичной системы счисления
- 26. Скачать презентанцию
Добрый день☺ Итак, сегодня мы проводим урок информатике дистанционно. От Вас потребуется 45 минут внимания и высокой концентрации. Во время занятия мы будем обращаться к «Агенту» для более активного общения
Слайды и текст этой презентации
Слайд 3Что будем делать?☺
Сегодня мы познакомимся с переводом чисел
из одной системы счисления в другую, но сначала вспомним тему
предыдущих занятий…….….повторим
Слайд 4Давайте вместе ответим на вопросы:
Система счисления – это …
символический метод
записи чисел, представление чисел с помощью письменных знаков.
Основание системы
счисления – это … это количество различных знаков или символов (цифр), используемых для отображения чисел в данной системе
Системы счисления бываю …
Системы счисления бывают позиционные и непозиционные.
В троичной системе счисления основание равно …
трем
Позиционная система счисления отличается от непозиционной?
в позиционной системе счисления количественное значение каждой цифры зависит от ее места (позиции) в числе. В непозиционной системе счисления (римская, русская, вавилонская) цифры не меняют своего количественного значения при изменении их расположения в числе.
Слайд 5А можно ли переводить числа из одной системы счисления в
другую?
Конечно да, и сейчас мы научимся это делать☺
Слайд 6перевод чисел из системы счисления с основанием n в десятичную
Любое
число можно представить в виде суммы произведений составляющих его цифр
на соответствующие степени основания системы. На этом принципе основан перевод чисел из любой СС в десятичную СС:Хn = an · bn + … + a0 · b0 + a-1 · b-1 + ...
Соглашусь с Вами, с первого взгляда это формула может вызвать много вопросов. Давайте более подробно рассмотрим ее на примерах:
Слайд 7Перевод чисел из системы счисления с основанием n в десятичную
перевод
чисел из двоичной системы счисления с основанием в десятичную
перевод чисел
из восьмеричной счисления с основанием n в десятичнуюперевод чисел из шестнадцатеричной системы счисления с основанием n в десятичную
дальше
Слайд 8Для перевода двоичного числа в десятичное необходимо это число представить
в виде суммы произведений степеней основания двоичной системы счисления на
соответствующие цифры в разрядах двоичного числа.Например, требуется перевести двоичное число 10110110 в десятичное. В этом числе 8 цифр и 8 разрядов ( разряды считаются, начиная с нулевого, которому соответствует младший бит). В соответствии с уже известным нам правилом представим его в виде суммы степеней с основанием 2:
Читаем текст и одновременно смотрим на пример
101101102 = (1·27)+(0·26)+(1·25)+(1·24)+(0·23)+(1·22)+(1·21)+(0·20) = 128+32+16+4+2 = 18210
назад
Слайд 9Для перевода восьмеричного числа в десятичное необходимо это число представить
в виде суммы произведений степеней основания восьмеричной системы счисления на
соответствующие цифры в разрядах восьмеричного числа.Например, требуется перевести восьмеричное число 2357 в десятичное. В этом числе 4 цифры и 4 разряда ( разряды считаются, начиная с нулевого, которому соответствует младший бит). В соответствии с уже известным нам правилом представим его в виде суммы степеней с основанием 8:
Читаем текст и одновременно смотрим на пример
23578 = (2·83)+(3·82)+(5·81)+(7·80) = 2·512 + 3·64 + 5·8 + 7·1 = 126310
назад
Слайд 10Для перевода шестнадцатеричного числа в десятичное необходимо это число представить
в виде суммы произведений степеней основания шестнадцатеричной системы счисления на
соответствующие цифры в разрядах шестнадцатеричного числа.Например, требуется перевести шестнадцатеричное число F45ED23C в десятичное. В этом числе 8 цифр и 8 разрядов (помним, что разряды считаются, начиная с нулевого, которому соответствует младший бит). В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
Читаем текст и одновременно смотрим на пример
F45ED23C16 =
(15·167)+(4·166)+(5·165)+(14·164)+(13·163)+(2·162)+(3·161)+(12·160) = 409985490810
назад
Слайд 11перевод чисел из системы счисления с основанием n в десятичную
Любое
число можно представить в виде суммы произведений составляющих его цифр
на соответствующие степени основания системы. На этом принципе основан перевод чисел из любой СС в десятичную СС:Хn = an · bn + … + a0 · b0 + a-1 · b-1 + ...
Соглашусь с Вами, с первого взгляда это формула может вызвать много вопросов. Давайте более подробно рассмотрим ее на примерах:
назад
Слайд 12Перевод чисел из десятичной системы счисления в систему счисления с
основанием n
Для перевода чисел из десятичной системы счисления в двоичную
используют так называемый "алгоритм замещения", состоящий из следующей последовательности действий: Делим десятичное число А на N. Частное Q запоминаем для следующего шага, а остаток a записываем как младший бит n-го числа.
Если частное q не равно 0, принимаем его за новое делимое и повторяем процедуру, описанную в шаге 1. Каждый новый остаток записывается в разряды двоичного числа в направлении от младшего бита к старшему.
Алгоритм продолжается до тех пор, пока в результате выполнения шагов 1 и 2 не получится частное Q = 0 и остаток < n .
Слайд 16Пример 3. Перевести число 50010 в шестнадцатеричную систему счисления.
Ответ: 500(10)=1F4(16).
Слайд 17Тренировочные упражнения
Перевести числа из десятичной системы счисления в двоичную, восьмеричную
и шестнадцатеричную
а) 2310= ;
б) 15610= ;2) Перевести числа в десятичную систему счисления
а) 100112= ; б) 5128= ; а) B416= ;
Слайд 19Ответы
Перевести числа из десятичной системы счисления в двоичную, восьмеричную и
шестнадцатеричную
а) 2310= 101112 ;
278;
1716;
б) 15610= 101111002 ;
2348;
9С16;
Слайд 20Ответы
2) Перевести числа в десятичную систему счисления
а)
100112= 1910 ;
б) 5128= 33010 ;
в) B416= 18010 ;
Если есть ошибки, обязательно еще раз все проверти.
Слайд 21Подведем итоги:
Итак, сегодня мы познакомились с алгоритмами перевода
некоторых систем счисления в другие системы счисления и узнали:
Вывод1
Вывод2
Вывод3
Слайд 22перевод чисел из системы счисления с основанием n в десятичную
Любое
число можно представить в виде суммы произведений составляющих его цифр
на соответствующие степени основания системы. На этом принципе основан перевод чисел из любой СС в десятичную СС:Хn = an · bn + … + a0 · b0 + a-1 · b-1 + ...
Соглашусь с Вами, с первого взгляда это формула может вызвать много вопросов. Давайте более подробно рассмотрим ее на примерах:
назад
Слайд 24При переводе «вручную» чисел из одной системы счисления в другую,
надо быть внимательным и терпеливым☺.
Слайд 25Домашнее задание
Перевести числа из десятичной системы счисления в двоичную, восьмеричную
и шестнадцатеричную
а) 4510= ;
б) 3410= ;2) Перевести числа в десятичную систему счисления
а) 10012= ; б) 6118= ; а) А516= ;
Теги