Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логика – наука о формах и способах мышления
Содержание
- 1. Логика – наука о формах и способах мышления
- 2. Понятие –это форма мышления, фиксирующая основные, существенные признаки объекта.СодержаниеОбъем
- 3. Высказывание - это форма мышления, в
- 4. Умозаключение - -это форма мышления, с
- 5. Алгебра высказыванийЛогическое умножение (конъюнкция)Логическое сложение (дизъюнкция)Логическое отрицание (инверсия)
- 6. Логическое умножение (конъюнкция)Составное высказывание, образованное в результате
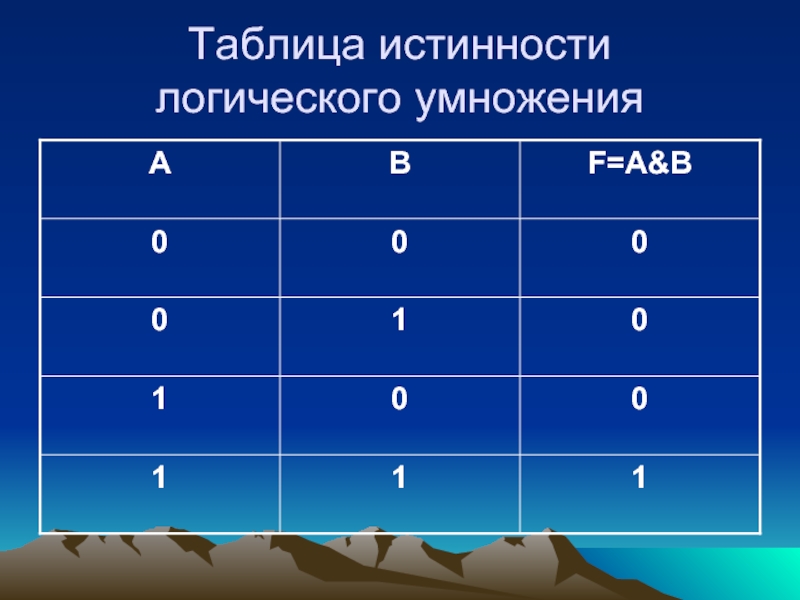
- 7. Таблица истинности логического умножения
- 8. Логическое сложение (дизъюнкция)Составное высказывание, образованное в результате
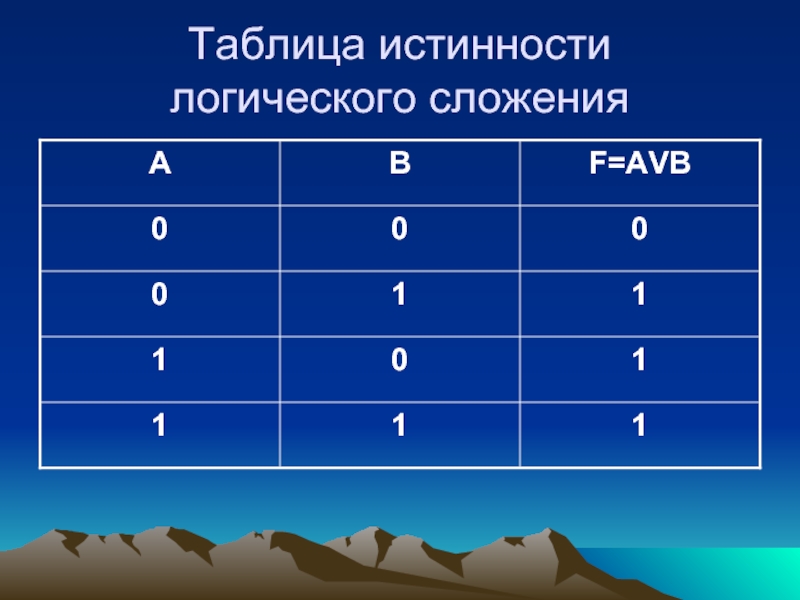
- 9. Таблица истинности логического сложения
- 10. Логическое отрицание (инверсия) Делает истинное высказывание ложным и наоборот, ложное - истинным.«не», а,
- 11. Таблица истинности функции логического отрицания
- 12. Логическое равенство (эквивалентность)Составное высказывание, образованное с помощью
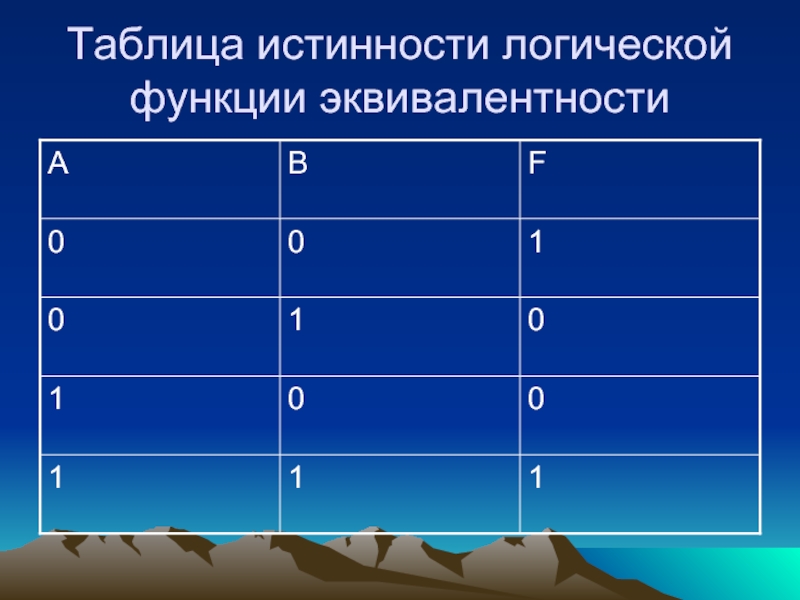
- 13. Таблица истинности логической функции эквивалентности
- 14. Логическое следование (импликация)Составное высказывание, образованное с помощью
- 15. Таблица истинности
- 16. Логические выражения (формулы) Логические переменныеЗнаки логических операций
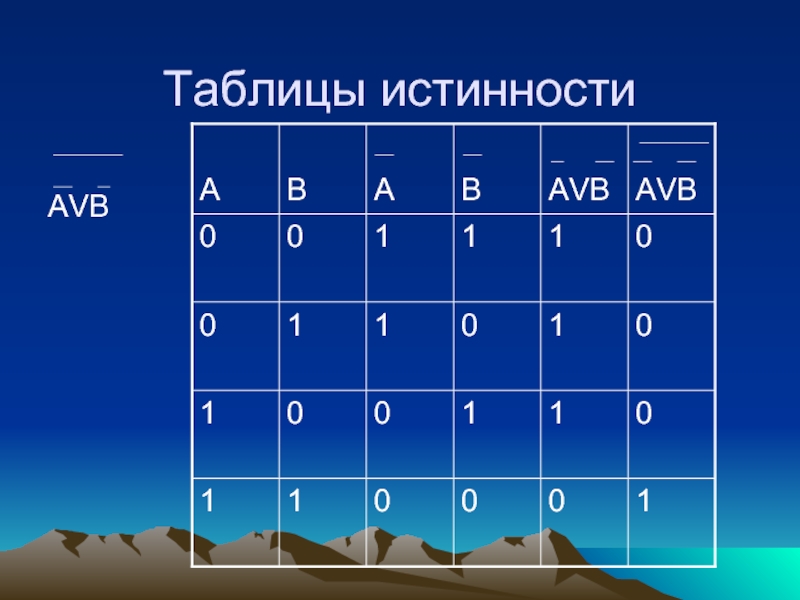
- 17. Таблицы истинностиAVB
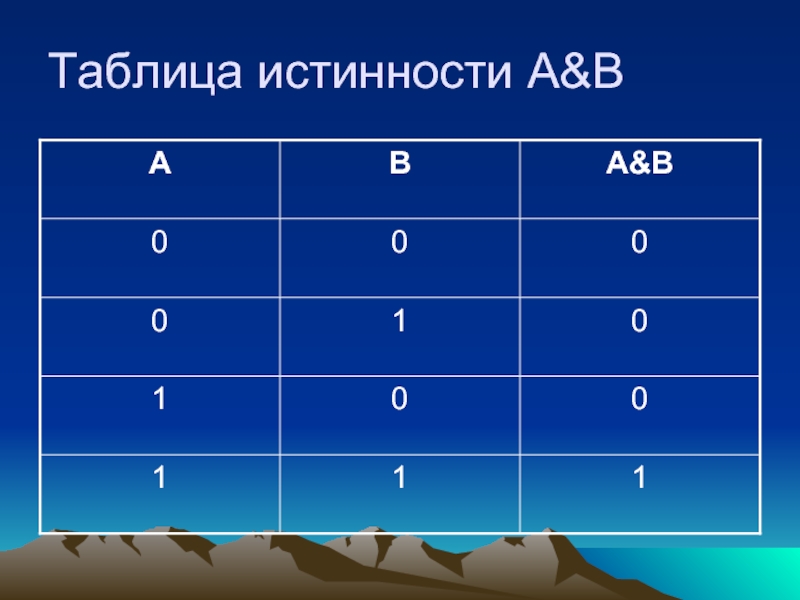
- 18. Таблица истинности A&B
- 19. Логические законы1. Закон тождестваА=А2. Закон непротиворечия А&А=03.Закон исключенного третьегоAVА=14.Закон двойного отрицания А=А
- 20. 5. Законы де МорганаАVВ=A&B A&B=AVB
- 21. 6. Закон коммутативностиA&B=B&AAVB=BVA
- 22. 7. Закон ассоциативности(A&B)&C=A&(B&C)(AVB)VC=AV(BVC)
- 23. 8. Закон дистрибутивности(A&B)V(A&C)=A&(BVC)(AVB)&(AVC)=AV(B&C)
- 24. Диктант1. Напишите таблицу истинности для операции конъюнкция.2.
- 25. Тест1. С помощью таблицы истинности получите результат
- 26. 3.Дана логическая схема. Напишите по ней логическую функцию и составьте таблицу истинности.V&VХУА
- 27. 4.Упростите выражение:A&BV(C&B)
- 28. 5. Для составления цепочек используются бусины A,
- 29. Скачать презентанцию
Понятие –это форма мышления, фиксирующая основные, существенные признаки объекта.СодержаниеОбъем
Слайды и текст этой презентации
Слайд 2Понятие –это форма мышления,
фиксирующая основные, существенные признаки объекта.
Содержание
Объем
Слайд 4Умозаключение -
-это форма мышления, с помощью которой из
одного или нескольких суждений (посылок) может быть получено новое суждение
(заключение).Слайд 5Алгебра высказываний
Логическое умножение (конъюнкция)
Логическое сложение (дизъюнкция)
Логическое отрицание (инверсия)
Слайд 6Логическое умножение (конъюнкция)
Составное высказывание, образованное в результате операции логического умножения
истинно тогда и только тогда, когда истинны все входящие в
него простые высказывания.«и», &,
Слайд 8Логическое сложение (дизъюнкция)
Составное высказывание, образованное в результате логического сложения (дизъюнкции),
истинно тогда, когда истинно хотя бы одно из входящих в
него простых высказываний.«Или», v
Слайд 10Логическое отрицание
(инверсия)
Делает истинное высказывание ложным и наоборот, ложное
- истинным.
«не», а,
Слайд 12Логическое равенство (эквивалентность)
Составное высказывание, образованное с помощью логической операции эквивалентности
истинно тогда и только тогда, когда оба высказывания одновременно либо
ложны, либо истинны.«…тогда и только тогда, когда …»
Слайд 14Логическое следование (импликация)
Составное высказывание, образованное с помощью операции логического следования
(импликации) ложно тогда и только тогда, когда из истиной предпосылки
следует ложный вывод.Слайд 19Логические законы
1. Закон тождества
А=А
2. Закон непротиворечия А&А=0
3.Закон исключенного третьего
AVА=1
4.Закон двойного
отрицания А=А
Слайд 24Диктант
1. Напишите таблицу истинности для операции конъюнкция.
2. Напишите таблицу истинности
для операции дизъюнкция.
3. Напишите таблицу истинности для операции импликация.
4. Напишите
таблицу истинности для операции эквивалентность.Слайд 25Тест
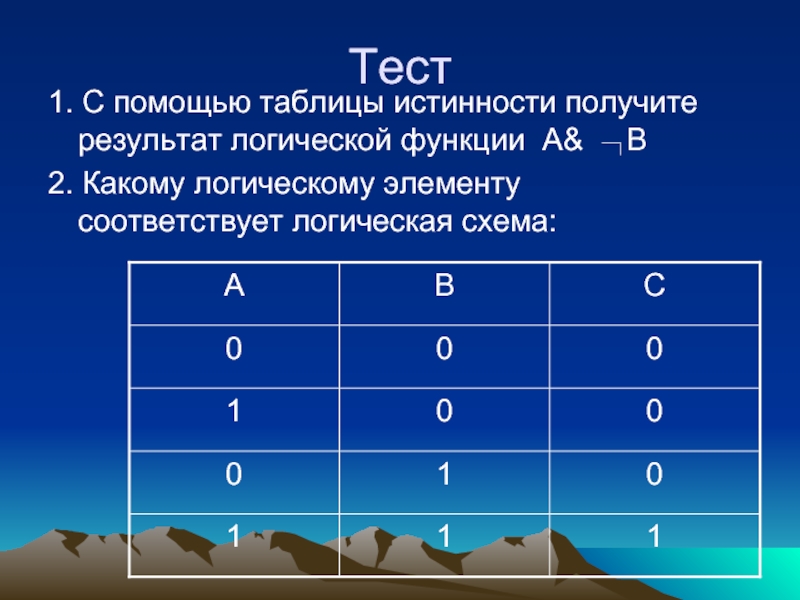
1. С помощью таблицы истинности получите результат логической функции A&
B
2. Какому логическому элементу соответствует логическая схема:
Слайд 26 3.Дана логическая схема. Напишите по ней логическую функцию и составьте
таблицу истинности.
V
&
V
Х
У
А
Слайд 28
5. Для составления цепочек используются бусины A, B,C, D,E. На
первом месте в цепочке стоит одна из бусин А, С,
Е. На втором – любая гласная, если первая буква согласная и любая согласная, если первая гласная. На третьем месте одна из бусин C,D,E, не стоящая в цепочке на 1-ом месте. Какая из цепочек создана по этому правилу?1)СВE 2)ADD 3)ECE 4)EAD
Теги