02.09.2020 Тема урока: Повторение курса геометрии 7 класс а

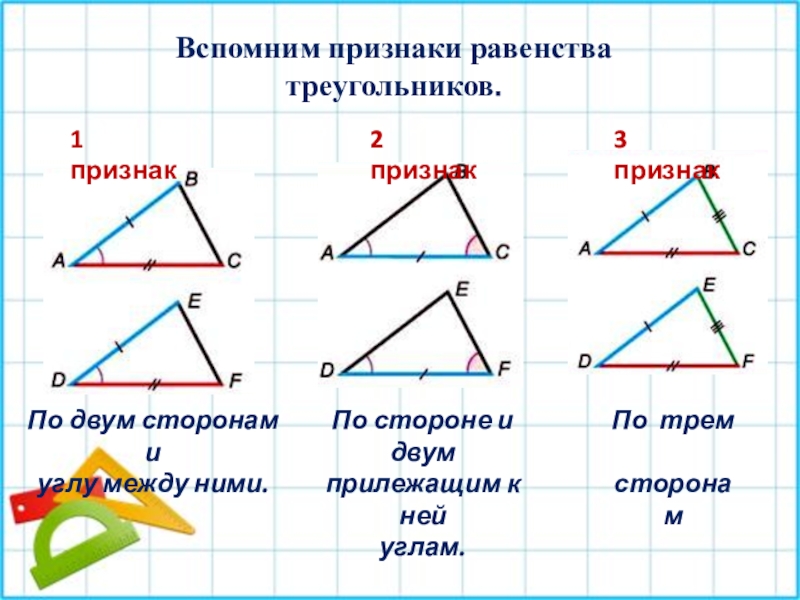
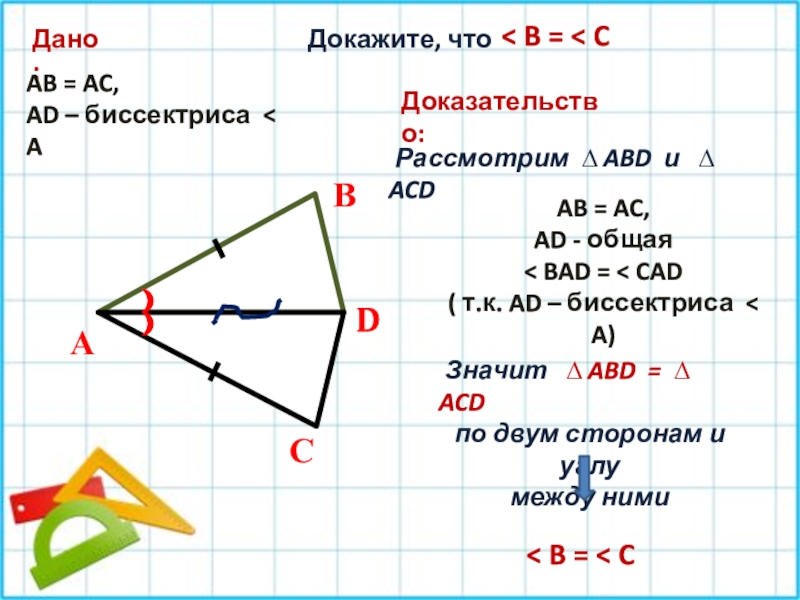
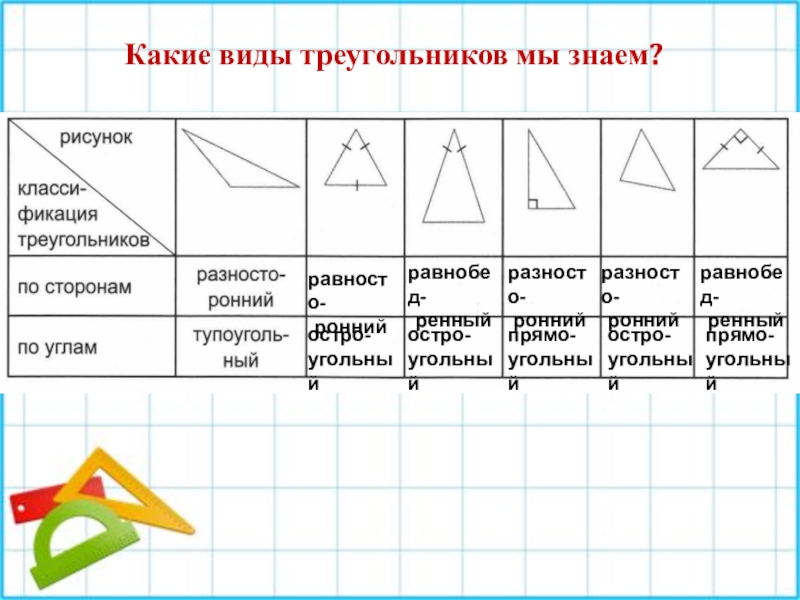
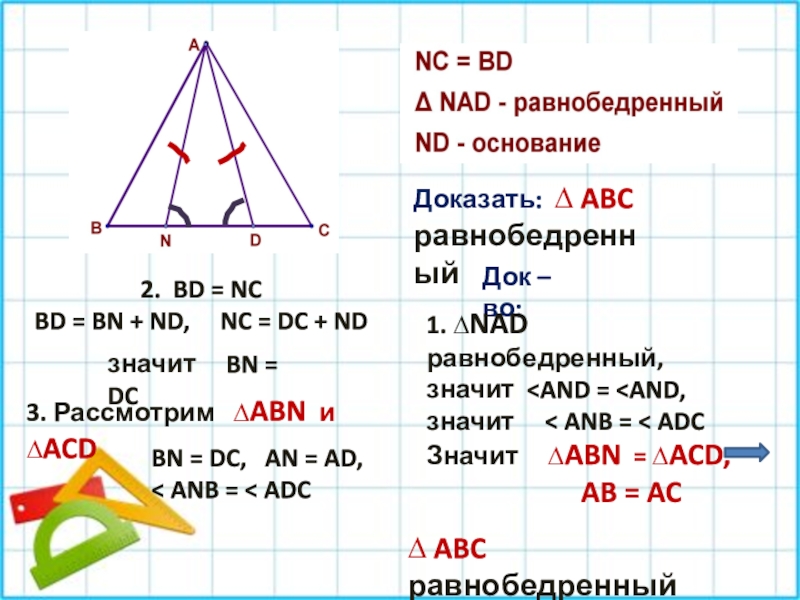
совместить наложением.
Если два треугольника равны, то равны их
соответственные углы

∆ АВС = ∆ MKP

AB = MK, BC = KP, AC = MP

< A = < M, < B = < K, < C = < P.

углу между ними.
По стороне и двум
прилежащим к ней
углам.
По трем
сторонам

= < CDA (по условию)
Значит ∆ ABD =

биссектриса < A
Рассмотрим ∆ ABD и ∆ ACD
Доказательство:
AB

Значит ∆ ABD = ∆ ACD
по двум сторонам и углу
между ними

< B = < C

= BD
< D = 480
Решение:
Рассмотрим ∆ ABC и

AB = CD, AC = BD
(по условию)
DC - общая

Значит ∆ ABC и ∆ DCB

< A = < D = 480

Ответ:

< A = 480

= BC - боковые стороны
AC - основание
Свойства равнобедренного

В равнобедренном треугольнике
углы при основании равны.

2. В равнобедренном треугольнике
медиана, проведенная к основанию
является также биссектрисой и
высотой.

= 600 , PC = 3. Найдите катет ВС.
Решение:
1.

= BN + ND, NC = DC +

значит BN = DC

1. ∆NAD равнобедренный,
значит значит < ANB = < ADC

BN = DC, AN = AD,
< ANB = < ADC

3. Рассмотрим ∆ABN и ∆ACD

Значит ∆ABN = ∆ACD,
AB = AC

∆ ABC равнобедренный

площадей на практике.
2. Пифагор и его теорема.
3. Бесподобное подобие.
4. Замечательные

Алгебра:

История открытия иррациональных чисел.
Извлечение квадратных корней без калькулятора.

Квадратные уравнения в трудах Диофанта
и Аль-Хорезми. Нестандартные способы решения
квадратных уравнений