Слайд 11. История возникновения понятия «алгоритм»
2. Цели, задачи и
практическое применение теории алгоритмов
3. Формализация понятия и свойства алгоритмов
4.
Виды алгоритмов
4.1. Линейные алгоритмы
4.2. Разветвляющиеся алгоритмы
4.3. Циклические алгоритмы
Алгоритмы основные понятия, свойства и виды.
Слайд 2«Алгоритм – это конечный набор правил, который определяет
последовательность операций для
решения конкретного множества
задач и обладает пятью важными чертами: конечность,
определённость, ввод,
вывод, эффективность» (Д. Э. Кнут).
«Алгоритм – это всякая система вычислений, выполняемых по
строго определённым правилам, которая после какого-либо числа
шагов заведомо приводит к решению поставленной задачи» (А.
Колмогоров).
«Алгоритм – это точное предписание, определяющее
вычислительный процесс, идущий от варьируемых исходных
данных к искомому результату» (А. Марков).
«Алгоритм — точное предписание о выполнении в определённом
порядке некоторой системы операций, ведущих к решению всех
задач данного типа» (Философский словарь под ред. М. М.
Розенталя).
1. История возникновения понятия «алгоритм»
Слайд 32. Цели, задачи и практическое применение теории алгоритмов:
формализация понятия «алгоритм»
и исследование формальных алгоритмических систем;
формальное доказательство алгоритмической неразрешимости задач;
классификация
задач, определение и исследование сложностных классов;
получение явных функций трудоемкости в целях сравнительного анализа алгоритмов;
разработка критериев сравнительной оценки качества алгоритмов.
Слайд 4ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ РЕЗУЛЬТАТОВ ТЕОРИИ
АЛГОРИТМОВ
Теоретический аспект
При исследовании некоторой задачи позволяет ответить
на вопросы:
1) является задача в принципе алгоритмически разрешимой?
При утвердительном ответе,
анализируют временные затраты на получения
точного решения для больших размерностей исходных данных.
Практический аспект
Методы и методики теории алгоритмов позволяют осуществить:
рациональный выбор из известного множества алгоритмов решения
задачи с учетом особенностей их применения (например, при
ограничениях на размерность исходных данных или объема
дополнительной памяти);
получение временных оценок решения сложных задач;
разработку и совершенствование эффективных алгоритмов решения
задач в области обработки информации на основе практического
анализа.
Слайд 5Формализация понятия алгоритма
Определение 1. Алгоритм – это заданное на некотором
языке конечное
предписание, задающее конечную последовательность выполнимых
элементарных операций для решения задачи,
общее для класса возможных исходных данных.
Определение 2. Алгоритм – точный набор инструкций, описывающих
порядок действий исполнителя для достижения результата решения
задачи за конечное время.
3. Формализация понятия и свойства алгоритмов
Слайд 6Свойства алгоритмов
Дискретность — алгоритм должен представлять процесс решения задачи
как последовательное
выполнение некоторых простых шагов. Для
выполнения каждого шага алгоритма требуется конечный
отрезок времени,
то есть преобразование исходных данных в результат осуществляется во
времени дискретно.
Детерминированность — определённость. В каждый момент времени
следующий шаг работы однозначно определяется состоянием системы.
Таким образом, алгоритм выдаёт один и тот же результат (ответ) для одних
и тех же исходных данных.
Слайд 7Понятность — алгоритм для исполнителя должен включать только те
команды, которые
ему (исполнителю) доступны, которые входят в его
систему команд.
Завершаемость (конечность) —
при корректно заданных исходных данных
алгоритм должен завершать работу и выдавать результат за конечное число
шагов. Вероятностный алгоритм может и никогда не выдать результат, но
вероятность этого равна 0.
Массовость — универсальность. Алгоритм должен быть применим к
разным наборам исходных данных.
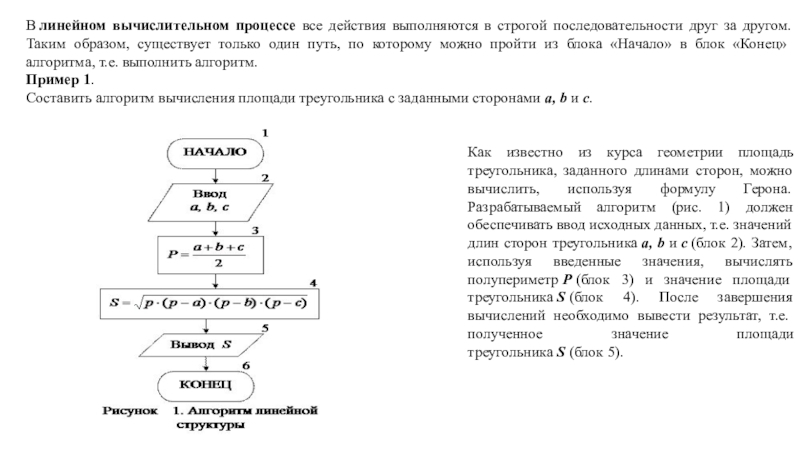
Слайд 10В линейном вычислительном процессе все действия выполняются в строгой последовательности друг
за другом. Таким образом, существует только один путь, по которому
можно пройти из блока «Начало» в блок «Конец» алгоритма, т.е. выполнить алгоритм.
Пример 1.
Составить алгоритм вычисления площади треугольника с заданными сторонами a, b и с.
Как известно из курса геометрии площадь треугольника, заданного длинами сторон, можно вычислить, используя формулу Герона. Разрабатываемый алгоритм (рис. 1) должен обеспечивать ввод исходных данных, т.е. значений длин сторон треугольника a, b и с (блок 2). Затем, используя введенные значения, вычислять полупериметр Р (блок 3) и значение площади треугольника S (блок 4). После завершения вычислений необходимо вывести результат, т.е. полученное значение площади треугольника S (блок 5).
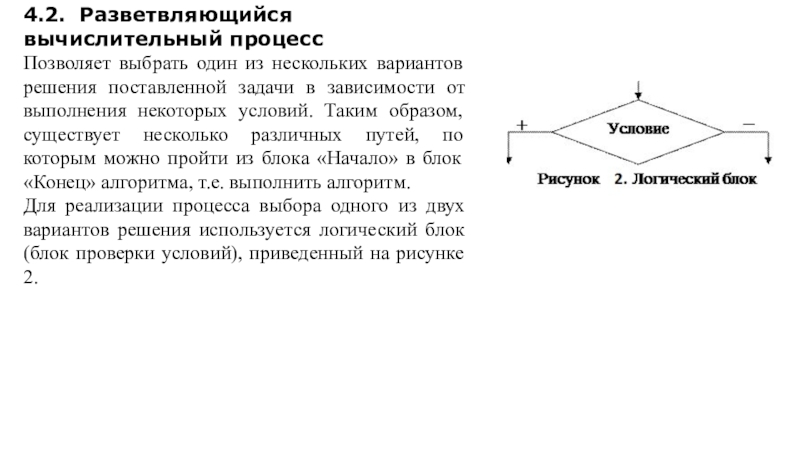
Слайд 114.2. Разветвляющийся вычислительный процесс
Позволяет выбрать один из нескольких вариантов решения
поставленной задачи в зависимости от выполнения некоторых условий. Таким образом,
существует несколько различных путей, по которым можно пройти из блока «Начало» в блок «Конец» алгоритма, т.е. выполнить алгоритм.
Для реализации процесса выбора одного из двух вариантов решения используется логический блок (блок проверки условий), приведенный на рисунке 2.
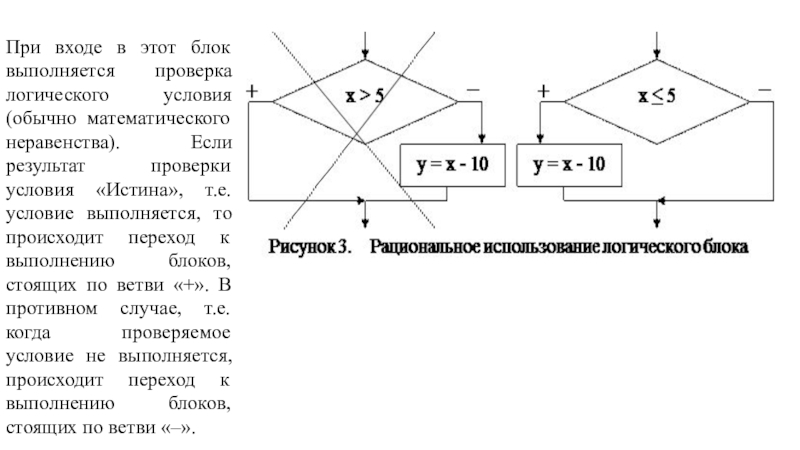
Слайд 12При входе в этот блок выполняется проверка логического условия (обычно
математического неравенства). Если результат проверки условия «Истина», т.е. условие выполняется,
то происходит переход к выполнению блоков, стоящих по ветви «+». В противном случае, т.е. когда проверяемое условие не выполняется, происходит переход к выполнению блоков, стоящих по ветви «–».
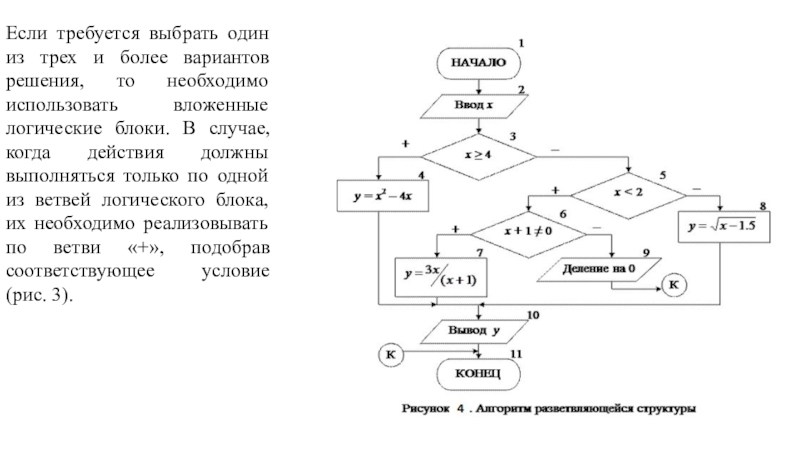
Слайд 13Если требуется выбрать один из трех и более вариантов решения,
то необходимо использовать вложенные логические блоки. В случае, когда действия
должны выполняться только по одной из ветвей логического блока, их необходимо реализовывать по ветви «+», подобрав соответствующее условие (рис. 3).
Слайд 14При выполнении вычислений необходимо учитывать область определения математических функций. Следовательно,
вначале необходимо проверить возможность вычисления данного математического выражения при текущих
значениях исходных данных, т.е. проверить «аномалию». К наиболее часто встречающимся «аномалиям» относятся: операция деления (на 0 делить нельзя), вычисление квадратного корня (подкоренное выражение должно быть ≥ 0), вычисление логарифма (выражение под знаком логарифма должно быть > 0), вычисление tg, ctg. В случае возникновения «аномалии» (невозможно выполнить вычисления) необходимо пропустить все действия, которые зависят от вычисляемой величины, и перейти в ту часть алгоритма, где можно продолжить вычисления.
Слайд 15Пример 2. Составить блок-схему алгоритма, вычисляющего значение у по одной из трех формул,
в зависимости от значения х.
Слайд 16Исходными данными для решения поставленной задачи является значение х, которое вводится
в блоке 2. Затем в блоке 3 проверяется 1-е ограничение
(х≥4), в случае его выполнения происходит переход к блоку 4, в котором вычисляется значение у по 1-й формуле. Если результатом проверки 1-го условия является «ЛОЖЬ» (это означает, что х < 4), то необходимо проверить одно из двух оставшихся условий. Обычно выбирается более «короткое» ограничение (в блоке 5 проверяется 3-е ограничение). Если х < 2, то необходимо вычислять y по 3-й формуле, в которой может возникнуть «аномалия» – деление на 0, поэтому в блоке 6 проверяется неравенство знаменателя дроби нулю. И только после этого в блоке 7 вычисляется значение у. В том случае, когда невозможно вычислить значение у по 3-й формуле, выводится сообщение о возникновении ошибки (блок 9) и выполняется переход на конец алгоритма. И, наконец, если значение х не удовлетворяет ни 1-му, ни 3-му ограничению, значит, выполняется 2-е ограничение и у вычисляется по 2-й формуле (блок 8). Эта формула также содержит «аномалию» – подкоренное выражение должно быть ≥ 0. Однако, проверять её не надо, так как при любом значении х, попадающем в интервал [2; 4[, подкоренное выражение всегда > 0. Не зависимо от того, по какой формуле будет вычислено значение у его надо вывести на экран, поэтому выходы блоков 4, 7 и 8 объединяются и происходит переход к блоку 10, в котором выводится у.

Слайд 174.3. В алгоритмах циклической структуры выполнение одних и тех же действий может
повторяться несколько раз. Организация циклического вычислительного процесса выполняется в несколько
этапов:
1-й этап – подготовка к выполнению цикла. На этом этапе задаются начальные значения для параметра цикла и переменных, использующихся для хранения накапливающихся величин (сумма, количество или произведение вычисляемых величин). Параметр цикла – это переменная, на основе которой строится цикл. Она должна удовлетворять трем условиям: являться исходной величиной для выполнения вычислений; изменяться по определенному закону (чаще всего это закон арифметической прогрессии); оказывать влияние на условие завершения повторяющихся вычислений.
2-й этап – тело цикла. Оно содержит арифметические и логические действия, которые могут повторяться определенное количество раз. В конце тела цикла обязательно должен быть блок, в котором изменяется значение параметра цикла.
3-й этап – условие выхода из цикла, которое предотвращает бесконечное выполнение цикла. С помощью этого условия проверяется надо ли повторять вычисления, или выходить из цикла.

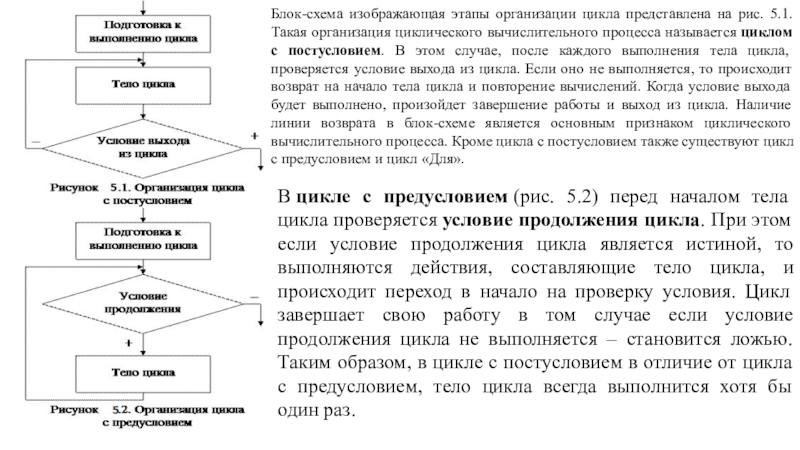
Слайд 18Блок-схема изображающая этапы организации цикла представлена на рис. 5.1. Такая
организация циклического вычислительного процесса называется циклом с постусловием. В этом случае,
после каждого выполнения тела цикла, проверяется условие выхода из цикла. Если оно не выполняется, то происходит возврат на начало тела цикла и повторение вычислений. Когда условие выхода будет выполнено, произойдет завершение работы и выход из цикла. Наличие линии возврата в блок-схеме является основным признаком циклического вычислительного процесса. Кроме цикла с постусловием также существуют цикл с предусловием и цикл «Для».
В цикле с предусловием (рис. 5.2) перед началом тела цикла проверяется условие продолжения цикла. При этом если условие продолжения цикла является истиной, то выполняются действия, составляющие тело цикла, и происходит переход в начало на проверку условия. Цикл завершает свою работу в том случае если условие продолжения цикла не выполняется – становится ложью. Таким образом, в цикле с постусловием в отличие от цикла с предусловием, тело цикла всегда выполнится хотя бы один раз.
Слайд 19Цикл «Для» реализуется на основе блока модификации и представляет собой
вариант цикла с предусловием, в котором предполагается, что часть действий
по организации цикла выполняется автоматически. Работа цикла «Для» более подробно будет рассмотрена в последующих разделах.
Цикл, в состав которого не входят другие циклы, называется простым.
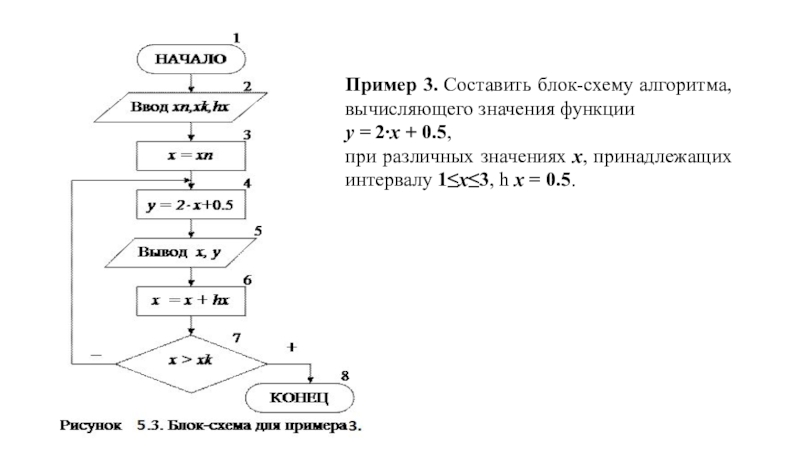
Слайд 20Пример 3. Составить блок-схему алгоритма, вычисляющего значения функции
у = 2∙x + 0.5,
при
различных значениях х, принадлежащих интервалу 1≤x≤3, h x = 0.5.
Слайд 21Таблица 1. Пошаговое выполнение цикла
Где ] [ обозначают целую часть
выражения.
Слайд 22Циклические вычислительные процессы, для которых можно вычислить количество шагов цикла
без выполнения алгоритма, называются циклами с известным числом повторений. Для реализации
циклов с известным числом повторений можно равноценно использовать любой из трех стандартных типов цикла (с постусловием, с предусловием, «Для»).
Если в цикле при выполнении вычислений может возникнуть «аномалия», то завершать выполнение алгоритма, как в разветвляющемся вычислительном процессе, не надо. В этом случае необходимо пропустить все операции, использующие переменную, значение которой невозможно вычислить, и выполнить переход к блоку, в котором изменяется значение параметра цикла, т.е. продолжить работу цикла. При следующем значении параметра цикла «аномалия» может не возникнуть, и работа цикла пойдет естественным путем.
Слайд 23Часто наряду с циклическим вычислением значений величины или совокупности величин
необходимо определить сумму, произведение или количество всех получаемых значений или
некоторых из них.
При выполнении суммирования и вычислении произведения или количества рационально использовать принцип постепенного накапливания значений величин, получаемых на каждом шаге цикла. Для хранения таких «накапливающихся» величин используются дополнительные переменные, которым предварительно необходимо задать начальные значения. Обычно это делается на этапе подготовки к выполнению цикла. В качестве начального значения для суммы и количества используется ноль, для произведения – единица.
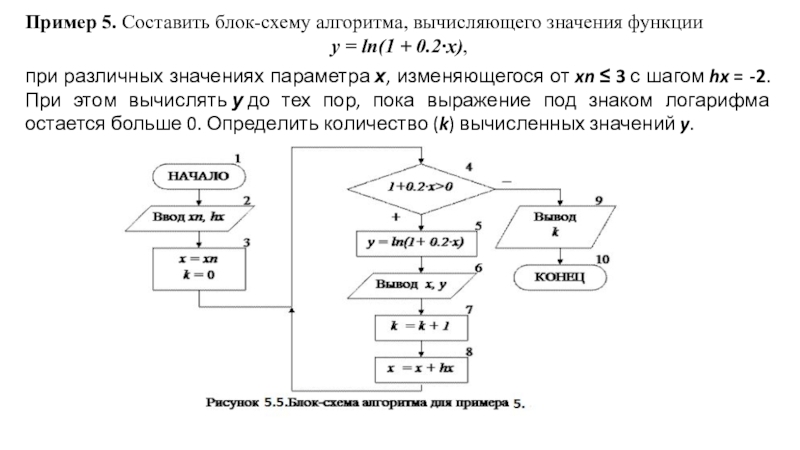
Слайд 24Пример 5. Составить блок-схему алгоритма, вычисляющего значения функции
у = ln(1 +
0.2∙x),
при различных значениях параметра х, изменяющегося от xn ≤ 3 с шагом hx = -2. При
этом вычислять у до тех пор, пока выражение под знаком логарифма остается больше 0. Определить количество (k) вычисленных значений y.














![1. История возникновения понятия алгоритм
2. Цели, задачи и практическое Таблица 1. Пошаговое выполнение циклаГде ] [ обозначают целую часть выражения. Таблица 1. Пошаговое выполнение циклаГде ] [ обозначают целую часть выражения.](/img/tmb/6/507700/d58bdd442cfeaf374d07acf9ee3c7de0-800x.jpg)