Слайд 1Практическое занятие 11
Следствия из уравнений Максвелла:
распространение электромагнитных волн (ЭМВ)
в
пространстве, свойства ЭМВ,
скорость распространения ЭМВ в вакууме и
среде.
Интенсивность ЭМВ.
Шкала ЭМВ.
Интерференция света: опыт Юнга,
интерференция в тонких пленках (нормальное падение).
Дифракция света.
Дифракционная решетка, как спектральный прибор.
Поляризация света.
Законы Малюса и Брюстера. Поляриметр.
Поглощение и рассеяние света.
Слайд 2Система уравнений Максвелла:
Слайд 3Решение системы уравнений:
Уравнения, описывающие периодические процессы:
во времени для отдельной точки
пространства;
в пространстве для совокупности точек
в данный момент времени
Е0, В0
– амплитуды колебаний электрического и
магнитного полей
– циклическая частота колебаний
– волновое число
Слайд 5Следствия:
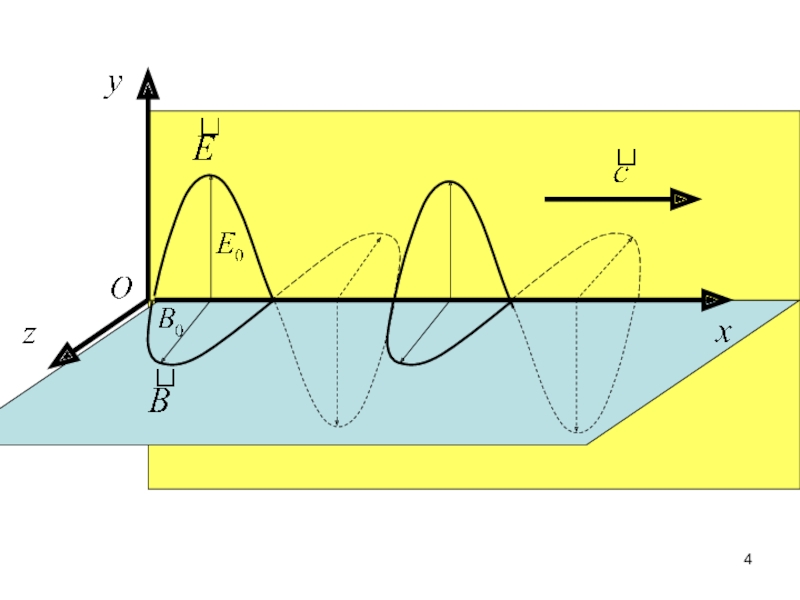
ЭМВ – волна, характеризуется колебаниями
не частиц среды, а взаимосвязанных
полей:
изменяющихся во времени и пространстве
электрического и магнитного полей
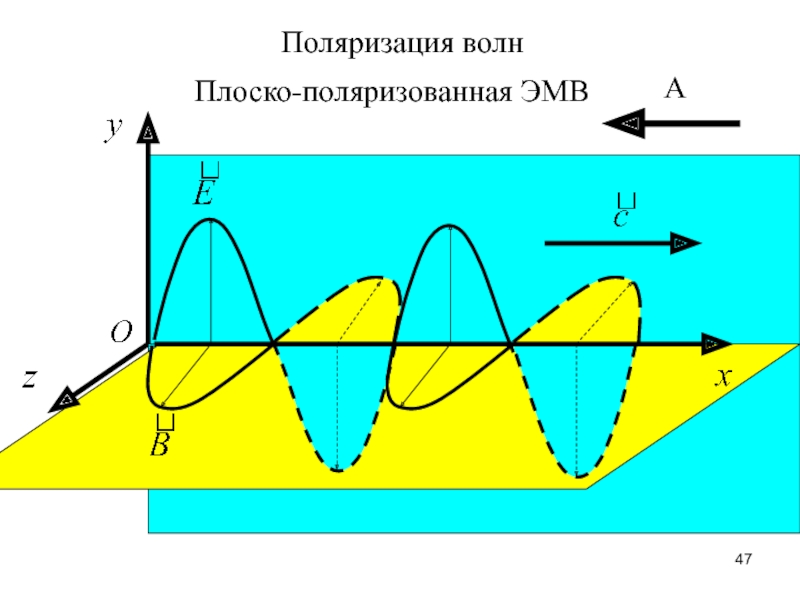
2. ЭМВ – поперечная волна: вектор
напряженности электрического поля колеблется
перпендикулярно направлению распространения волны
(именно составляющая электрического поля
определяет ощущение зрения),
вектор индукции магнитного поля колеблется в
перпендикулярной плоскости.
Слайд 63. Источниками ЭМВ являются движущиеся с
переменной скоростью (ускорением) заряженные
частицы (f.eg.:электроны в атоме при переходе из одного
стационарного состояния в
другое для световых волн
и ЭМВ больших частот)
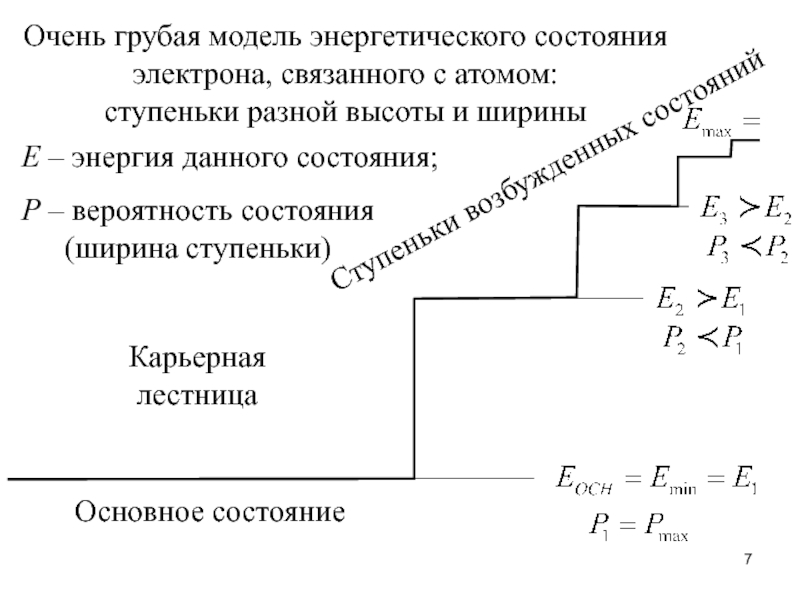
Слайд 7Очень грубая модель энергетического состояния
электрона, связанного с атомом:
ступеньки разной высоты
и ширины
Ступеньки возбужденных состояний
Е – энергия данного состояния;
Р –
вероятность состояния
(ширина ступеньки)
Основное состояние
Карьерная
лестница
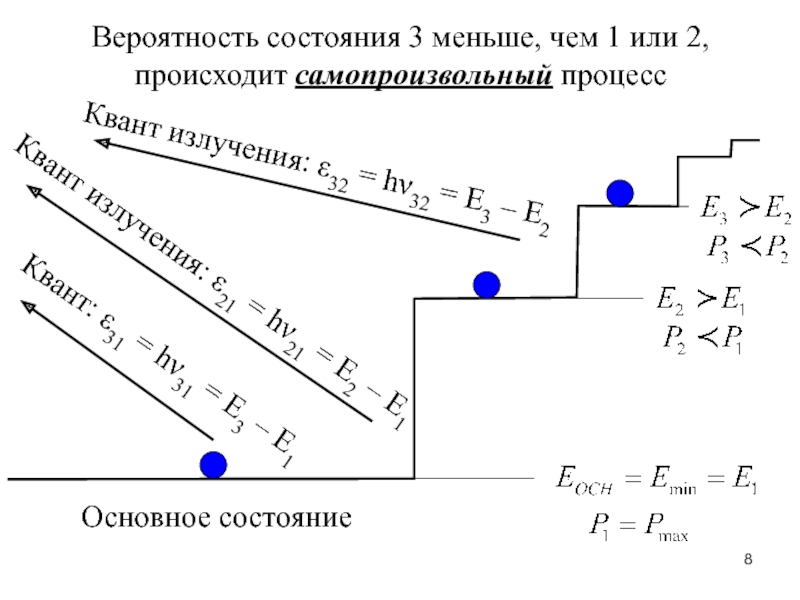
Слайд 8Основное состояние
Вероятность состояния 3 меньше, чем 1 или 2,
происходит самопроизвольный
процесс
Квант излучения: ε32 = hν32 = Е3 – Е2
Квант излучения:
ε21 = hν21 = Е2 – Е1
Квант: ε31 = hν31 = Е3 – Е1
Слайд 9Источник «длинных» ЭМВ: LC – контур:
+
-
Вывод: частота ЭМВ определяется только
свойствами
источника излучения
Слайд 104. Скорость распространения ЭМВ в вакууме:
5. Скорость распространения ЭМВ
в среде:
Длина ЭМВ в вакууме:
Слайд 11Показатель преломления среды относительно вакуума
Скорость распространения света в среде:
Длина волны
в среде:
6. Интенсивность световой волны
(энергия, переносимая световой волной за единицу
времени
через единичную поверхность):
Слайд 12Колебательный контур аппарата для терапевтической
диатермии состоит из катушки индуктивности
и
конденсатора емкостью С = 30 мкФ. Определить
индуктивность катушки,
если частота генератора 1,0 МГц.
СИ:
С = 30 мкФ =
f = 1,0 МГц =
Слайд 13В физиотерапии часто применяются электромагнитные
волны с частотой 460 МГц.
Определить длину волны в
воздухе (ε = 1,00) и в мягких тканях (ε =
1,40).
СИ:
Воздух:
Ткани:
Слайд 14На какой частоте суда передают сигнал бедствия,
если по международному
соглашению длина
радиоволны SОS равна 600 м?
В микроволновой терапии используются
ЭМВ в
дециметровом диапазоне λ1 = 65,0 см и сантиметровом
диапазоне λ2 = 12,6 см. Определить частоты этих волн.
СИ:
СИ:
λ1 = 65,0 см =
λ2 = 12,6 см =
Слайд 15Длина световой волны в вакууме равна 555 нм.
Определить частоту
волны, скорость распространения
волны и длину волны в воздухе и
воде.
Слайд 16Спектр ЭМВ
Радиоволны λ > 5·10-5 м (12 диапазонов)
Оптическое излучение
1 мм > λ > 10 нм
(ИК, видимое 780 нм
> λ > 380 нм, УФ)
Рентгеновское (Х – излучение) 10 нм > λ > 0,01 пм
γ – излучение 0,1 нм > λ
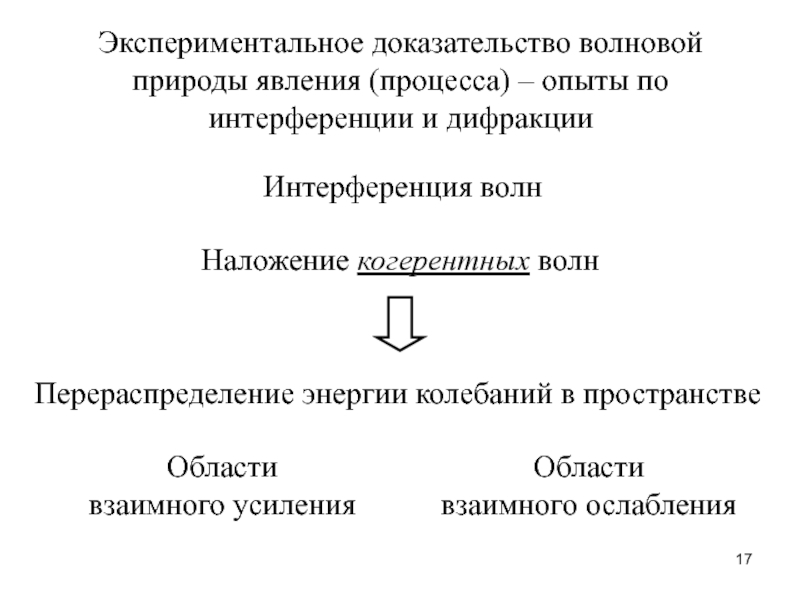
Слайд 17Экспериментальное доказательство волновой
природы явления (процесса) – опыты по
интерференции и дифракции
Интерференция волн
Наложение когерентных волн
Области
взаимного усиления
Перераспределение энергии колебаний в пространстве
Области
взаимного ослабления
Слайд 18Когерентные источники:
одинаковая частота (период) колебаний ω (Т);
неизменная во времени разность
фаз
колебаний φ0
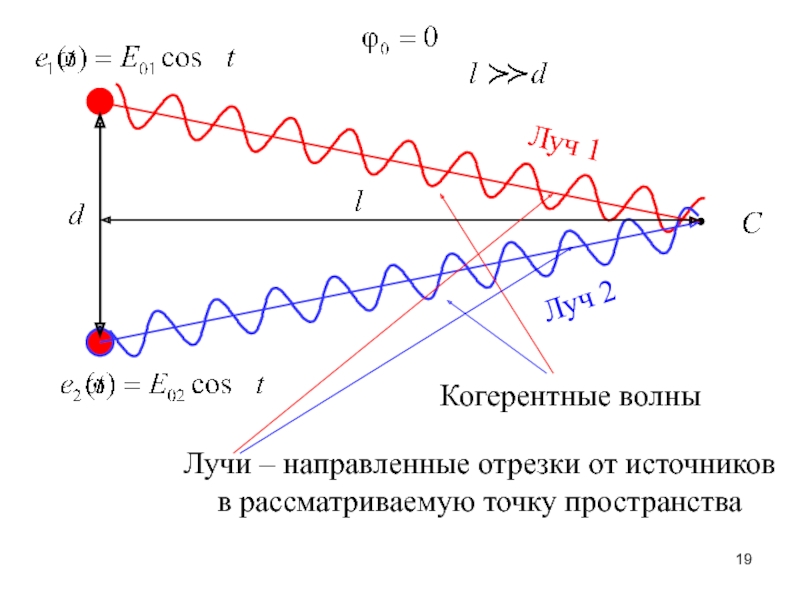
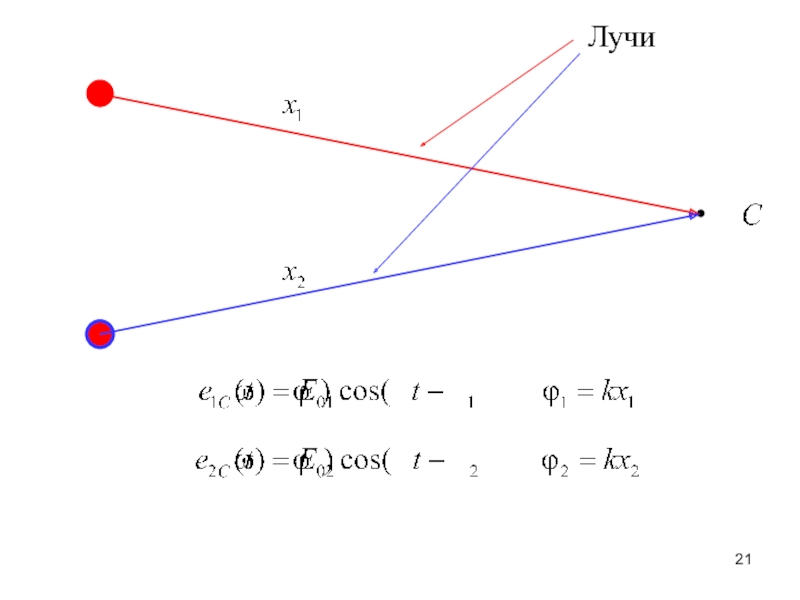
Слайд 19Когерентные волны
Лучи – направленные отрезки от источников
в рассматриваемую точку пространства
Луч
1
Луч 2
Слайд 20Колебания электрического поля в точке С:
– геометрическая длина луча
1
(геометрический ход луча 1)
Слайд 22Суммарное колебание электрического поля в точке С:
Уравнение колебания в точке
Слайд 23Амплитуда результирующего колебания в точке С:
(*)
(**)
Слайд 24Условие максимума амплитуды колебаний в точке С
(условие максимума интерференции):
Δх –
геометрическая разность хода лучей 1 и 2
(*) = (**)
Вывод:
Слайд 26Разность хода волн от двух когерентных источников
света равна 0,2
λ. Чему равна при этом разность фаз?
(**)
Разность хода волн от
двух когерентных источников
света в некоторой точке экрана равна Δх = 4,36 мкм.
Каков результат интерференции, если длина волны λ
равна: а) 670 нм; б) 438 нм; в) 536 нм?
рад. = º
Слайд 27Опыт Юнга по интерференции на двух щелях
(2 = ∞)
(результат может быть расширен на систему из
большего числа щелей):
Слайд 28(монохроматический свет)
е1
е2
Экран для наблюдения эффекта
е1 и е2 – когерентные источники
света
парадокс масштаба
Лучи 1 и 2 по существу параллельны
Слайд 29В точке А удаленного экрана наблюдается max
интерференции (светлая полоса):
На удаленном
экране наблюдается интерференционная,
симметричная относительно нулевого максимума
картина в виде
чередующихся светлых и темных полос
Результат расчета интерференционной картины
для двух щелей может быть расширен на систему
из большего числа параллельных щелей
Слайд 30Δх – геометрическая разность хода интерферирующих
лучей
Вывод: расчет результата интерференции сводится
1.К расчету разности хода интерферирующих лучей Δх
(геометрическая задача);
2. К проверке
полученного значения Δх на условия
max или min.
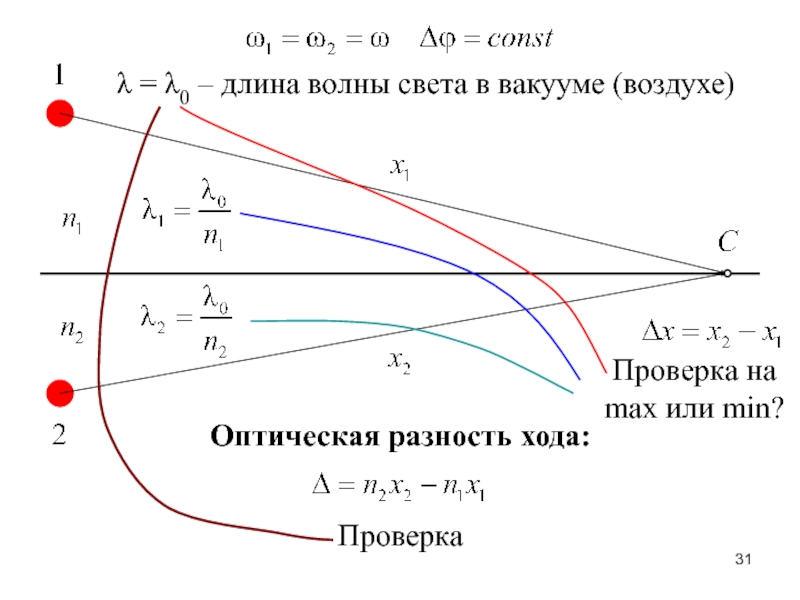
Слайд 31λ = λ0 – длина волны света в вакууме (воздухе)
Проверка
на
max или min?
Оптическая разность хода:
Проверка
Слайд 32При отражении света от оптически более плотной
среды (с большим показателем
преломления)
происходит смена фазы волны на противоположную,
что учитывается добавкой в
Δ слагаемого
Оптическая разность хода:
Слайд 33Мыльная пленка толщиной h = 0,3 мкм освещается
белым светом, падающим
перпендикулярно ее
поверхности (α = 0). Пленка рассматривается в
отраженном
свете. Показатель преломления мыльного
раствора равен n2 = 1,33.
Какого цвета будет при этом пленка?
h = 0,3 мкм =
Слайд 34падающий луч
луч, отраженный
от верхней поверхности
луч, прошедший
через пленку
луч, отраженный
от
нижней поверхности
интерференция в отраженном свете
Слайд 35Оптическая разность хода лучей:
Цвет пленки определяется условием максимума для
для
волны длиной λ:
Слайд 36Для просветления оптики применяют тонкие пленки.
Какой минимальной толщины должна
быть пленка,
чтобы пропускать без отражения свет длины волны
λ
= 550 нм? Показатель преломления пленки n1 = 1,22.
Показатель преломления стекла оптики n2 = 1,38.
Слайд 37Дифракционная решетка – спектральный прибор
a
b
d=a + b
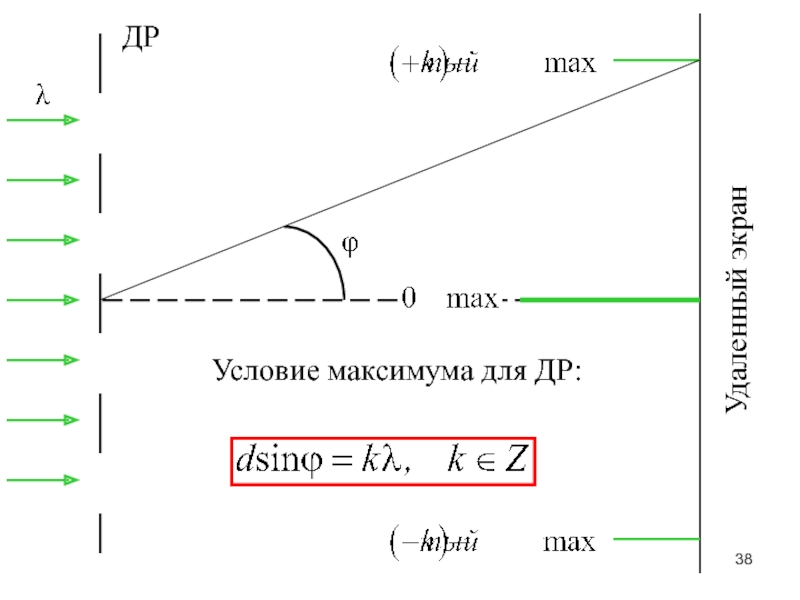
Слайд 38Удаленный экран
ДР
Условие максимума для ДР:
Слайд 39Определить период решетки шириной L = 2,5 см,
имеющей N
= 12500 штрихов.
Ответ записать в микрометрах.
Слайд 40Чему равна постоянная (период) дифракционной решетки,
если в спектре 2-го
порядка красная линия (700 нм)
видна под углом 30°?
Дифракционная решетка
содержит N = 500 штрихов на
L = 1 мм. Найти наибольший порядок спектра для света
с длиной волны λ = 680 нм.
Слайд 41Оранжевый свет с длиной волны 600 нм и зеленый свет
с длиной волны 540 нм проходят через
дифракционную решетку, имеющую
4000
штрихов на сантиметр. Чему равно угловое расстояние
между оранжевым и зеленым максимумами
третьего порядка?
Слайд 42Дифракционная решетка освещена нормально падающим
монохроматическим светом. В дифракционной картине
максимум второго порядка отклонен на угол φ1=14°.
На какой угол
φ2 отклонен максимум третьего порядка?
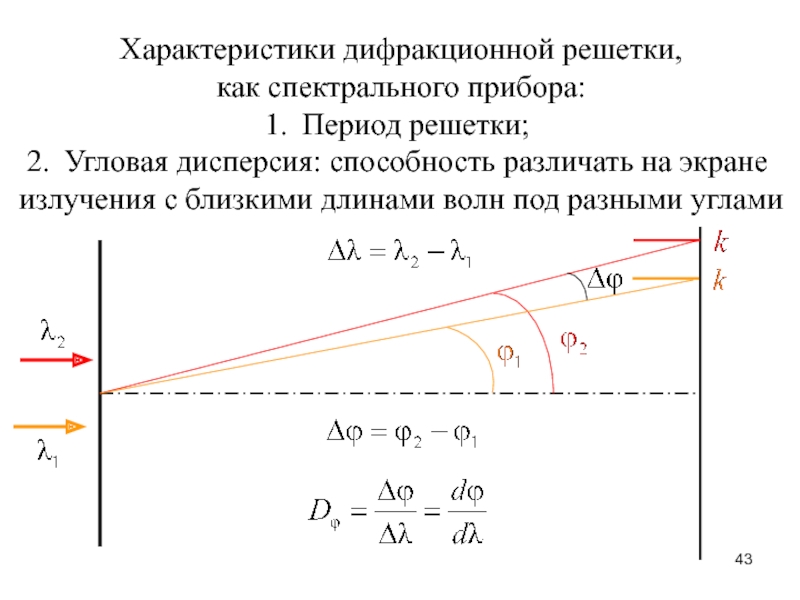
Слайд 43Характеристики дифракционной решетки,
как спектрального прибора:
Период решетки;
Угловая дисперсия: способность различать на
экране
излучения с близкими длинами волн под разными углами
Слайд 443. Разрешающая способность дифракционной решетки:
Слайд 45Дифракционную решетку с числом щелей
N = 10 000 используют
для исследования спектра света в области 600 нм.
Найти минимальную
разность длин волн, которую
можно обнаружить такой решеткой при наблюдении
максимумов второго порядка.
Слайд 46С помощью дифракционной решетки с периодом
d = 20 мкм
требуется разрешить дублет натрия
(λ1=589,0 нм и λ2=589,6 нм) в
спектре второго порядка.
При какой наименьшей длине l решетки это возможно?
Слайд 47А
Плоско-поляризованная ЭМВ
Поляризация волн
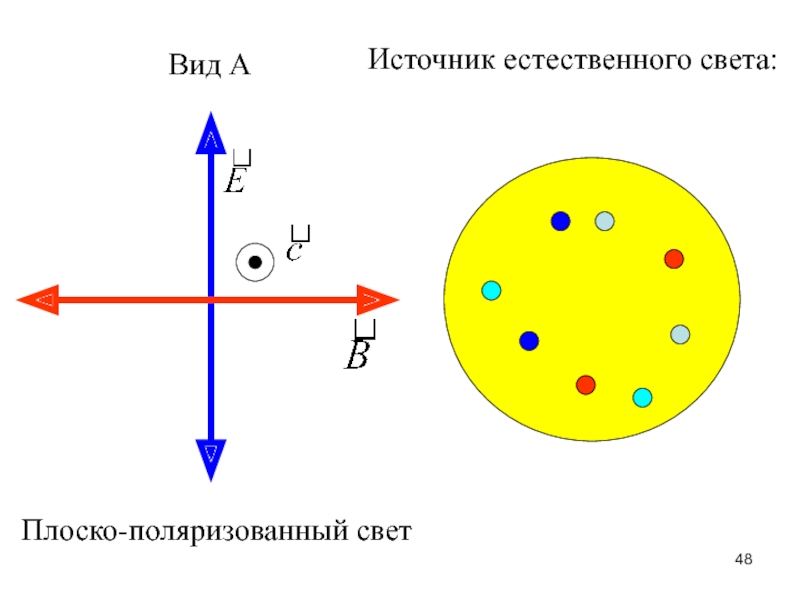
Слайд 48Вид А
Плоско-поляризованный свет
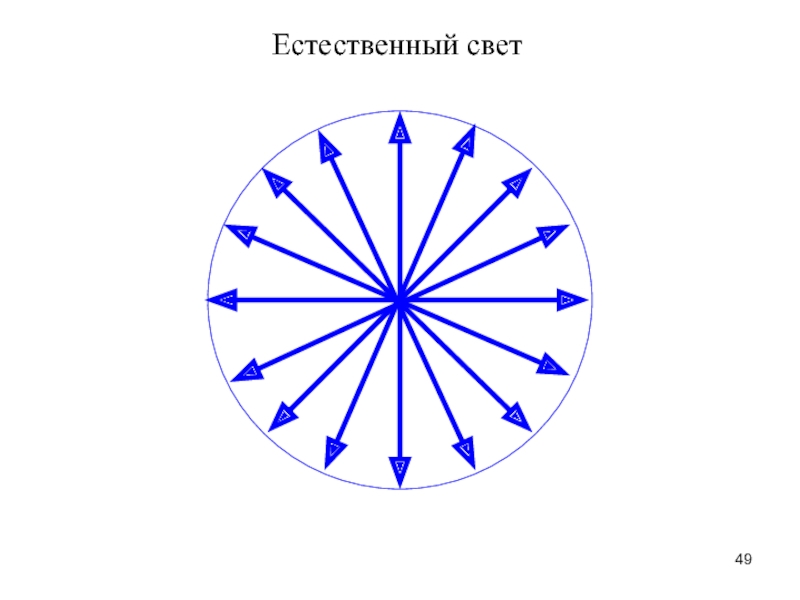
Источник естественного света:
Слайд 50Частично-поляризованный
свет
Плоско-поляризованный
свет
=
+
Естественный свет
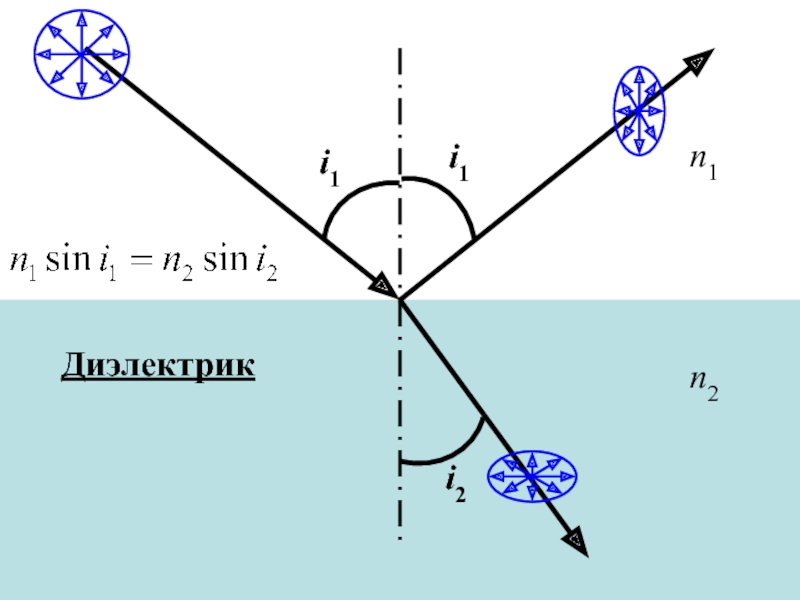
Слайд 53При какой высоте солнца над горизонтом солнечный
свет отражается от
поверхности озера
плоско-поляризованным? Показатель преломления
воды в области видимого света
n = 1,33.
Слайд 54Поляризатор
Анализатор
α
E0
E=E0 cosα
Слайд 56Чему равен угол φ между главными плоскостями
поляризатора и анализатора,
если интенсивность
естественного света, прошедшего через поляризатор
и анализатор, уменьшилась
в 4 раза?
Слайд 57Оптически активные вещества (ОАВ)
ОАВ
[α0] = град / % · м
[α0]
= град / м
Поляриметры (сахариметры)
Слайд 58Определить удельное вращение [α0] для раствора сахара,
если при прохождении
света через трубку с раствором
угол поворота плоскости поляризации равен
α = 22°.
Длина трубки равна L = 10 см, концентрация раствора
равна С = 0,33 г/см3.
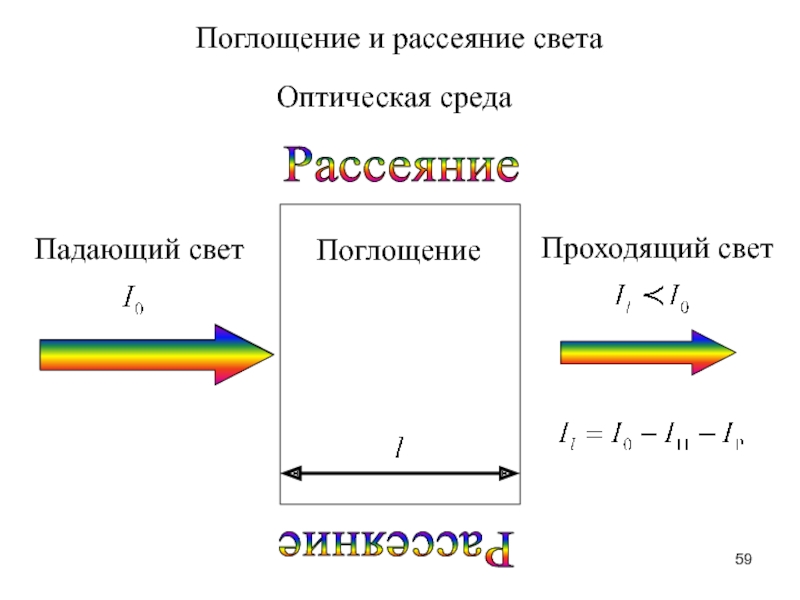
Слайд 59Оптическая среда
Падающий свет
Проходящий свет
Поглощение
Рассеяние
Рассеяние
Поглощение и рассеяние света
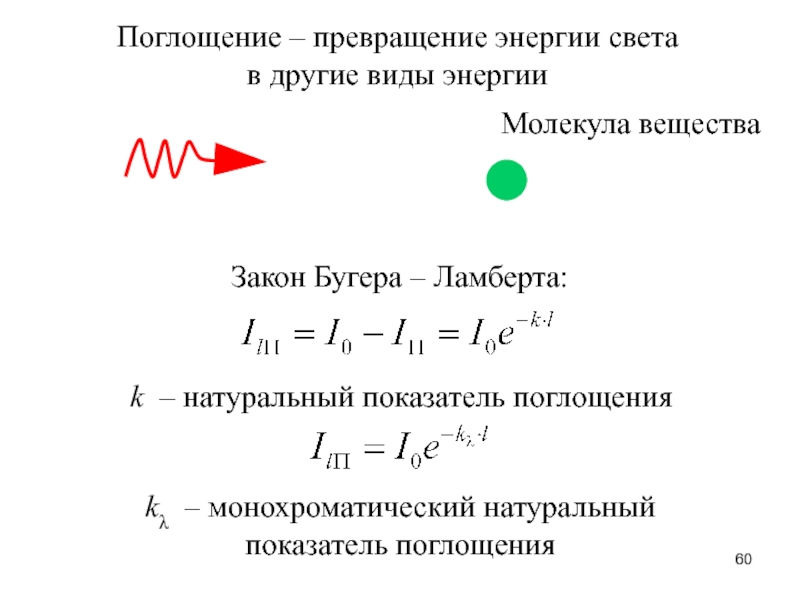
Слайд 60Поглощение – превращение энергии света
в другие виды энергии
Молекула вещества
Закон Бугера
– Ламберта:
k – натуральный показатель поглощения
kλ – монохроматический натуральный
показатель поглощения
Слайд 61Рассеяние происходит на
пространственных неоднородностях среды
Инородные малые частицы
Флуктуации плотности
(молекулярное
рассеяние)
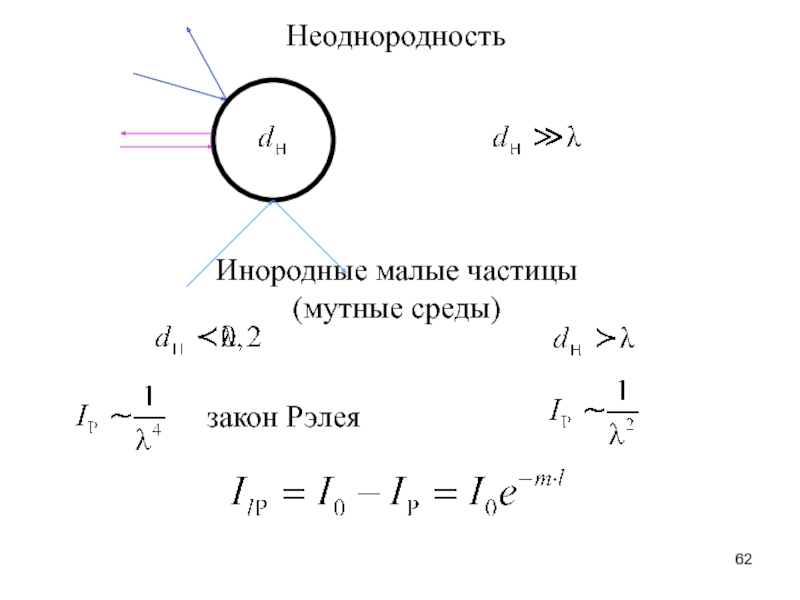
Слайд 62Неоднородность
Инородные малые частицы
(мутные среды)
закон Рэлея
![Оптически активные вещества (ОАВ)ОАВ[α0] = град / % · м[α0] = град / мПоляриметры (сахариметры)](/img/thumbs/c649da9b3e978ae36dd12baed3e25d49-800x.jpg "1
Практическое занятие 11
Следствия из уравнений Максвелла:
распространение Оптически активные вещества (ОАВ)ОАВ[α0] = град / % · м[α0] = град / мПоляриметры (сахариметры)")
![Определить удельное вращение [α0] для раствора сахара, если при прохождении света через трубку с раствором угол поворота](/img/tmb/3/247189/bf1cad2388afc17e104aaeb6ccdeaa1c-800x.jpg "1
Практическое занятие 11
Следствия из уравнений Максвелла:
распространение Определить удельное вращение [α0] для раствора сахара, если при прохождении света")
