6. 2. Интерпретации природы волн де Бройля. Волновой пакет как (неудачная)

модель частицы-волны. Волны вероятности
Итак, было установлено, что объекты, которые

принято представлять частицами (электроны, атомы, молекулы, нейтроны), обладают волновыми свойствами.
Предлагались разные варианты «интерпретаций волновой механики» – физических способов совмещения корпускулярных и волновых свойств в одном объекте.
Де Бройль предложил концепцию «двойного решения», предполагающее использование уравнений динамики, имеющих одновременно сингулярные и волновые решения. Волна-частица состоит из двух объектов разной физической природы. Движение частицы (сингулярности) направляется движением «волны-пилота». Эта концепция не получила признания. (Хотя была развита затем Дэвидом Бомом.)
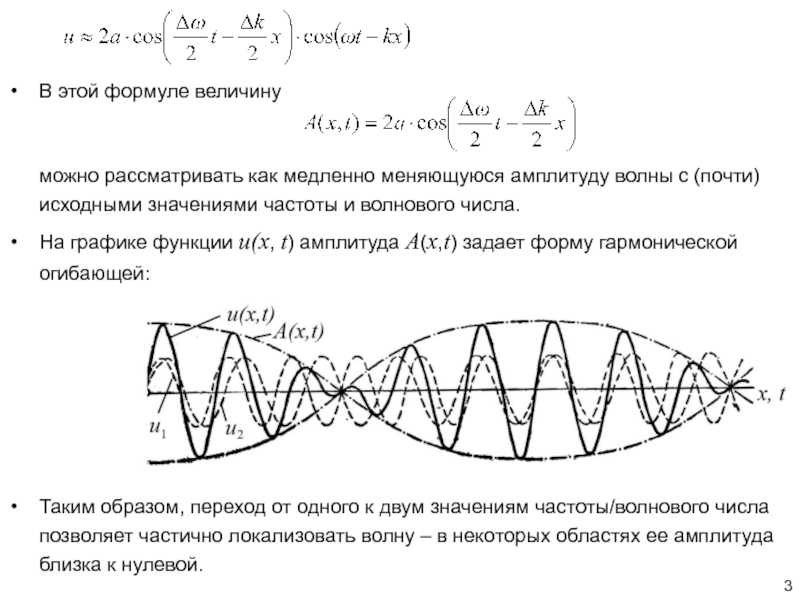
Но наиболее естественным поначалу казалось предположение, что частицы представляют собой «пакеты» волн некоторого материального (обладающего энергией) поля. Волновой «пакет» -- такая комбинация гармонических волн, для которой амплитуда поля велика лишь в ограниченной области пространства.
Плоская гармоническая волна де Бройля
с точно заданными значениями частоты и волнового вектора не соответствует обычным представлениям о частице, поскольку полностью делокализована.

x. Ограничимся лишь действительной частью функции.
Гармоническая волна с частотой

0 и волновым числом k0
u1(x,t) =acos(0t – k0x)
полностью делокализована, т.к. ее амплитуда не зависит от x и t.
Определим вторую волну с той же амплитудой и близкими значениями частоты и волнового числа:
u2(x,t) =acos(t – kx) ,
где k – k0=k и  – 0= – малые величины (<Сложим две эти волны, получив суммарную волну:


Заметим, что в аргументе второго косинуса присутствуют частота и волновой вектор, не сильно отличающиеся от  и k :

(В принципе, для (+0)/2 и (k+k0)/2 можно ввести и специальные обозначения.)

волны с (почти) исходными значениями частоты и волнового числа.
На графике

функции u(х, t) амплитуда А(x,t) задает форму гармонической огибающей:

Таким образом, переход от одного к двум значениям частоты/волнового числа позволяет частично локализовать волну – в некоторых областях ее амплитуда близка к нулевой.

потребовав постоянства аргумента косинуса (т.е. фазы). Например, его равенства нулю:

t – kx=0  x = (/k)t
Величину vф =  / k называют «фазовой скоростью волны».
Скорость перемещения максимумов огибающей («групповую скорость волны») можно получить, потребовав постоянства аргумента косинуса в выражении:

Нетрудно видеть, что групповая скорость выражается формулой vгр =  / k
В пределе малости  и k их отношение стремится к производной : vгр = d / dk
При условии  ~k («при линейном законе дисперсии») фазовая скорость совпадает с групповой.

нужно просуммировать бесконечное число волн.
Пусть параметр k (и соответствующая

частота ) непрерывно распределены в интервале ограниченной ширины [k0–k; k0+k]. Результат сложения таких элементарных волн (одинаковой амплитуды a) получим интегрированием:



Для вычисления интеграла требуется конкретизировать «закон дисперсии» (k). Считаем интервал k малым. Тогда произвольную дисперсионную зависимость (k) можно представить в виде ряда Тейлора:


Здесь через 0 , 0 и 0 обозначены значения функции (k) и ее производных при k=k0 (это некоторые числа).
Ограничимся первым членом разложения: .
При этом запомним, что погрешность этой формулы будет определяться в основном старшим отброшенным членом

функция от (k-k0). Косинус суммы преобразуется по тригонометрической формуле cos(+)=coscos–sinsin,

переход от dk к d(k-k0), интеграл от sin по симметричному интервалу =0). Опуская детали вычислений: результат может быть представлен в виде произведения «волнового» и медленно (при малом k) меняющуюся амплитудного
сомножителей.
u(x,t)  A(x,t)cos(0 t – k0 x)
Амплитуда:
,
где  = k(0 t – x)

«Мгновенный снимок» волнового пакета (в безразмерных координатах) при t=0 

,
где 

= k(0 t – x)


Свойства амплитудной функции: при   0 .
при  =  – и пакет пространственно ограничен размером x: таким, что xk=2 (запомнить для дальнейшего !).
В данном приближении, волновой пакет движется в пространстве, не меняя формы своей огибающей A(x,t).
Скорость его движения (групповую скорость ) можно определить из выражения для . Она равна v гр =0  d / dk (при k=k0).

«Мгновенный снимок» волнового пакета (в безразмерных координатах) при t=0 

,
где 

= k(0 t – x)



Фазовая скорость волн (скорость перемещения максимумов и минимумов внутри огибающей волнового пакета) определяется из верхнего уравнения и
равна v ф = 0 /k0 -- как и у отдельной гармонической волны со «средним» волновым числом k0.
Приведенные выше равенства являются точными, если закон дисперсии
линеен. При условии  =ck имеем: v ф = 0 / k0 =  / k = c = d / dk = v гр .
При этом волновой пакет перемещается как целое со скоростью c .
И, на первый взгляд, он представляется удачной моделью частицы-волны.

«Мгновенный снимок» волнового пакета (в безразмерных координатах) при t=0 

= p/ħ = (ħ/c) / ħ =  / c

– как и для классической электромагнитной волны.
Однако для частиц, обладающих массой покоя, закон дисперсии имеет иной вид.
Дисперсионную зависимость для них можно получить, используя уравнения де Бройля и выражение, связывающее энергию частицы с ее импульсом.
Уравнения де Бройля: и .
Простейшее нерелятивистское выражение для полной энергии свободной частицы с массой покоя m0:
соответствует закону дисперсии:
Эта зависимость нелинейна.
Точное релятивистское выражение: приводит к
– при m00 зависимость также нелинейна.
Следствие нелинейности: фазовая и групповая скорости непостоянны (зависят от k и ) и не равны друг другу.

 = ħ

 = m0c2+ p2/2m0

 2 = m02c4 + c2p2

скорости частицы p/m (!!).
С одной стороны, такое совпадение кажется

примечательным.
С другой – для стабильности волнового пакета требуется, чтобы составляющие его элементарные волны с разными k =p/ ħ распространялись с одинаковой скоростью. В противном случае, пакет со временем «расплывается».
Математически, расплывание волнового пакета связано с отброшенным при приближенном рассмотрении нелинейным членом дисперсионной зависимости


Его размерность – циклическая частота. Домножив на время  , получим величину неучтенного ранее отклонения фазы парциальной волны – составляющей волнового
пакета с наибольшим отклонением от «среднего» волнового числа k0 (оно
равняется k). Будем считать существенным отклонение фазы на  (вместо взаимного подавления составляющих волнового пакета со «средним» и «крайним» значениями волнового числа, они друг друга усиливают, или наоборот). Получаем условие:

частицы, получаем время расплывания волнового пакета


где x = 2 /k

– пространственный размер пакета.
Таким образом, время расплывания («время жизни») волнового пакета, описывающего массивную частицу оказывается конечным. Оно определяется ее массой и «размером».
Для макроскопических объектов оно велико.
Однако, для электрона (стабильной частицы) оценка дает весьма малые времена.
Для x = 10–10 м (порядка размера атома)  ~ 10–17 с;
для x = 10–15 м (порядка классического радиуса электрона)  ~ 10–26 с.

Таким образом, представление массивных частиц в виде волновых пакетов встречает значительные трудности, связанные с ограниченным временем жизни таких пакетов.
Однако данное возражение против такого представления – не единственное и даже не самое серьезное.

из них волновые пакеты) делятся на части.
Примеры:
преодоление полупрозрачных

границ с частичным отражением;
дифракция с образованием многих максимумов.
Но частицы (в частности, электроны) неделимы – это следует из экспериментов.
Была предложена еще одна интерпретация волн де Бройля, согласно которой волновые свойства присущи не отдельным частицам, а их потокам – то есть, волновые явления являются коллективными.
Эта гипотеза была опровергнута результатами специальных экспериментов.
Один из наиболее известных – опыт Л.М. Бибермана, Н.Г. Сушкина и В.А. Фабриканта (1949 г.). Опыт во многом аналогичен более ранним экспериментам со световыми потоками низкой интенсивности.
Схема эксперимента была подобна схеме опыта Томсона-Тартаковского. Для одного и того же образца (Ni) были получены электронограммы при высокой и при низкой интенсивности электронного потока, различавшихся на 7 порядков величины. Изображения оказались идентичными.

устройства (фотопластинки) было в 30 000 меньше среднего интервала между

моментами эмиссии последовательных электронов. Следовательно, в каждый момент в пространстве прибора присутствовало не более одного электрона.
Тем не менее, регистрировалась дифракционная картина в виде набора колец.
Вывод – волновые свойства (способность к дифракции) присущи отдельному электрону.

К опыту Бибермана, Сушкина и Фабриканта

В результате была принята статистическая интерпретация волн де Бройля как волн вероятности («копенгагенская интерпретация»).
Она базируется на идеях, сформулированных в 1926 г.
М. Борном.

Max Born (1882-1970)

наблюдаться непосредственно. Она представляет собой «волну вероятности».
Ее значение, точнее, квадрат

амплитуды комплекснозначной «волновой функции» , в каждой области пространства определяет вероятность обнаружения здесь описываемой частицы.
Поведение описываемой частицы, таким образом, является недетерминированным – оно не определяется полностью начальными условиями и не может быть описано иначе, чем через понятие вероятности.
Такой подход оказался правильным – то есть, продуктивным. Позволил получить согласие с экспериментом.
Выбор в качестве искомой комплекснозначной функции, к которой должен применяться принцип суперпозиции, позволяет описывать интерференционные явления. Результат сложения комплексных функции друг с другом определяется соотношением их фаз.
В то же время, наблюдаемым в эксперименте параметром волновой функции является квадрат амплитуды – действительная положительная величина, которая может быть сопоставлена вероятности события.

виде

представляется удачной. Это решение волнового уравнения для свободного пространства. Амплитуда

такой волны всюду одинакова. Так и должно быть – в свободном пространстве нет причин предпочесть одну область пространства другой. Фазовый множитель (экспонента) позволяет описывать интерференцию. Фаза определяется с точностью до постоянной.
Задача описания поведения частицы, таким образом, сводится к определению волновой функции для заданных условий – обычно для несвободной частицы. «Квантовая механика» -- теория нахождения таких решений.



Применим на качественном уровне статистическую (вероятностную) интерпретацию природы волн де Бройля к результатам эксперимента Бибермана, Сушкина и Фабриканта по дифракции отдельных электронов.

случайным.
Оно не зависит от мест прихода прочих электронов – поэтому

совпадение результатов измерений с потоками разной интенсивности естественно.
В то же время, вероятность прихода электрона в разные точки экрана неодинакова. Она пропорциональна квадрату амплитуды волновой функции, формирование которой является результатом интерференции волн вероятности.

К опыту Бибермана, Сушкина и Фабриканта

С приходом на пластинку многих электронов начинает «работать» закон больших чисел – относительная плотность распределения электронов по поверхности стремится к распределению вероятности.
Вследствие этого дифракционная картина (результат интерференции нематериальных волн вероятности) становится наблюдаемой.

Данная интерпретация позволяет совместить опытные факты дискретности (неделимости) электронов и их способности к дифракции.