Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Prez14.ppt
Содержание
- 1. Prez14.ppt
- 2. Пусть теперь волны распространяются в трёхмерной полости.
- 3. Условия существования стоячих волн в трёхмерной полости
- 4. Отметим, что при подсчёте стоячих волн приходящихся
- 5. Число точек, попадающих внутрь тонкого сферического слоя
- 6. Число стоячих волн приходящихся на интервал длин волн от λ до λ + dλ:
- 7. Формула Рэлея – Джинса.5.6.Ультрафиолетовая катастрофа.
- 8. Мы определили число степеней свободы электромагнитного излучения
- 9. Как мы показали ранее (см. п. 5.4)
- 10. Результат: согласие с экспериментом наблюдается только для
- 11. Формула Планка.5.7.Квантовая теория излучения.
- 12. Квантовая гипотеза ПланкаДля получения правильной зависимости спектральной
- 13. Основные приближения теории Планка.1. Как и в
- 14. Среднее значение энергии стоячих волн в полости
- 15. Это выражение можно преобразовать следующим образом. Предположим,
- 16. Знаменатель этой прогрессииследовательно прогрессия убывает.Сумма бесконечно убывающей геометрической прогрессии (|q|
- 17. Вычисляем производную:Подставляем полученный результат в формулу для средней энергии:Разделив числитель и знаменатель на e-x, получим:
- 18. Интересно отметить, что полученный результат в классическом
- 19. Спектральная плотность энергии излучения по Планку.Как было
- 20. Энергия электромагнитного излучения с частотами в интервале
- 21. Излучательная способность чёрного тела по Планку.Как было
- 22. Отметим, что при формула Планка переходит в
- 23. Излучательная способность чёрного тела по Планку. Сравнение с экспериментом.
- 24. Интегральная энергетическая светимость чёрного тела по Планку.Интегральная
- 25. Вычисление коэффициента σ даёт(Вт/(м2·К4). На самом деле,
- 26. Слайд 26
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Определение числа степеней свободы электромагнитного излучения в полости.
5.5.
5.5.3. Трёхмерный случай.
Слайд 3Условия существования стоячих волн в трёхмерной полости можно записать так:
Здесь
a, b, c – размеры трёхмерной плоскости.
Возможные значения волнового вектора
теперь образуют дискретное множество точек в трёхмерном фазовом пространстве волновых векторов.Каждому значению модуля волнового вектора соответствует одна стоячая волна. Для того, чтобы определить, сколько стоячих волн приходится на интервал значений волнового вектора от k до k + dk, нужно найти число точек в фазовом пространстве, попадающих внутрь тонкого сферического слоя толщиной dk.
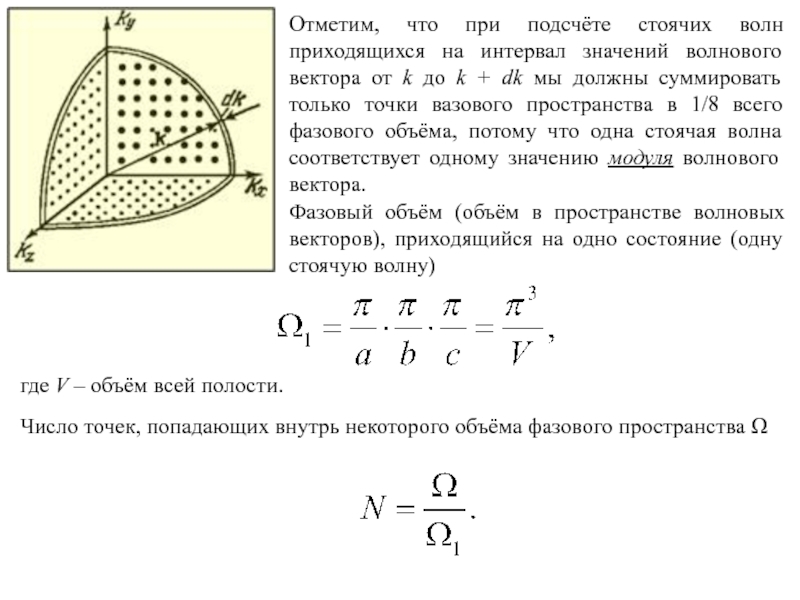
Слайд 4Отметим, что при подсчёте стоячих волн приходящихся на интервал значений
волнового вектора от k до k + dk мы должны
суммировать только точки вазового пространства в 1/8 всего фазового объёма, потому что одна стоячая волна соответствует одному значению модуля волнового вектора.Фазовый объём (объём в пространстве волновых векторов), приходящийся на одно состояние (одну стоячую волну)
где V – объём всей полости.
Число точек, попадающих внутрь некоторого объёма фазового пространства Ω
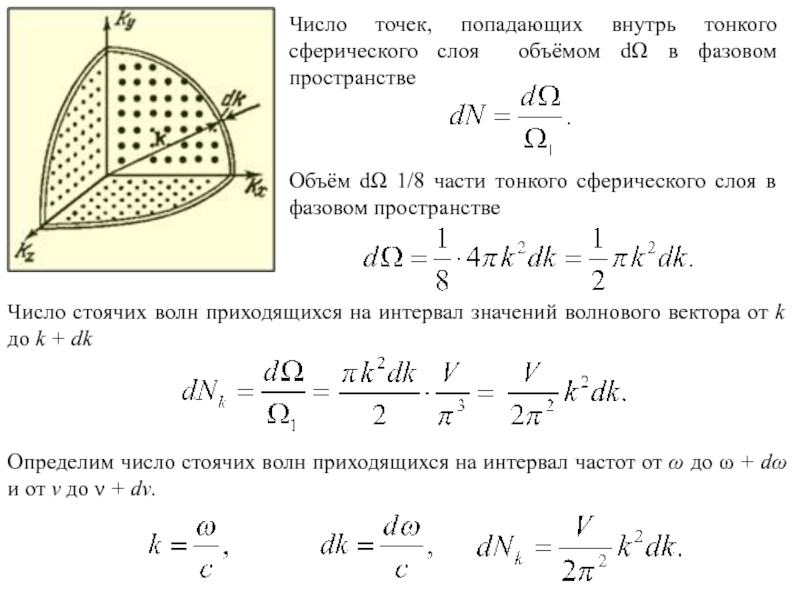
Слайд 5Число точек, попадающих внутрь тонкого сферического слоя объёмом dΩ в
фазовом пространстве
Объём dΩ 1/8 части тонкого сферического слоя в
фазовом пространстве Число стоячих волн приходящихся на интервал значений волнового вектора от k до k + dk
Определим число стоячих волн приходящихся на интервал частот от ω до ω + dω и от ν до ν + dν.
Слайд 8
Мы определили число степеней свободы электромагнитного излучения в полости вокруг
абсолютно чёрного тела, приходящееся на интервал частот от ω до
ω + dω .Энергия излучения в частотном интервале от ω до ω + dω
Вспомним определение спектральной плотности энергии электромагнитного излучения:
Итак, спектральная плотность энергии электромагнитного излучения в полости вокруг абсолютно чёрного тела
Слайд 9Как мы показали ранее (см. п. 5.4) плотность энергии электромагнитного
излучения в полости связана с излучательной способностью чёрного тела формулой
Теперь
мы можем найти излучательную способность чёрного тела.Для того, чтобы удобнее было сравнивать полученный результат с законом Вина, излучательную способность чёрного тела выразим через длину волны.
Нагретое тело находится в термодинамическом равновесии с излучением, поэтому температуры тела и излучения равны.
При λ → ∞ излучательная способность убывает, что согласуется с законом Вина. Но при λ → 0 r (λ, T) → ∞, что закону Вина противоречит.
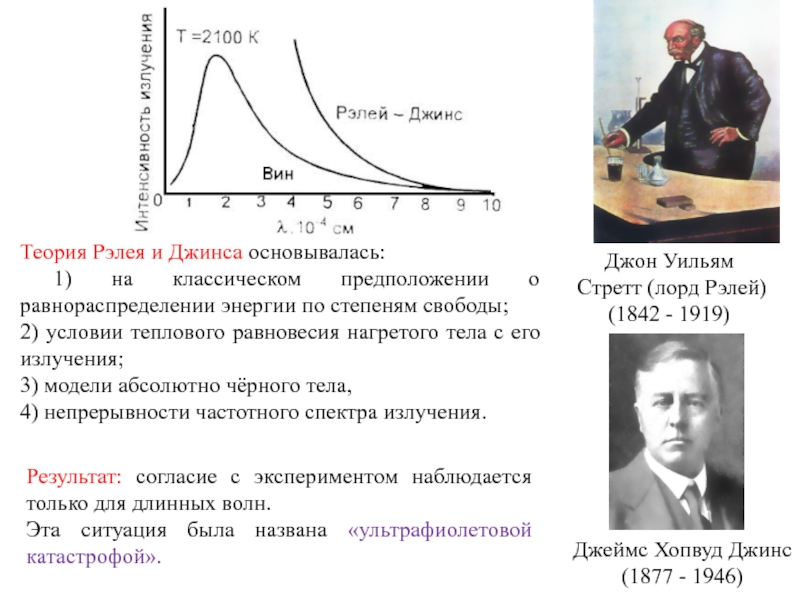
Слайд 10Результат: согласие с экспериментом наблюдается только для длинных волн.
Эта ситуация
была названа «ультрафиолетовой катастрофой».
Теория Рэлея и Джинса основывалась:
1) на
классическом предположении о равнораспределении энергии по степеням свободы;2) условии теплового равновесия нагретого тела с его излучения;
3) модели абсолютно чёрного тела,
4) непрерывности частотного спектра излучения.
Слайд 12Квантовая гипотеза Планка
Для получения правильной зависимости спектральной плотности излучения от
длины волны Планку пришлось отказаться в теории Рэлея и Джинса
от классического предположения о равнораспределении энергии по степеням свободы, а также предположить, что энергия может испускаться только порциями - квантами. Величина такой минимальной порции энергииE = hν.
Постоянная Планка
h = 6,626122 ·10-34 Дж ·с
Уже на следующий день после доклада Планка 19 октября 1900 г. один из его коллег, физик Рубенс, подтвердил экспериментально справедливость формулы Планка.
Слайд 13Основные приближения теории Планка.
1. Как и в теории Рэлея и
Джинса, используется модель абсолютно чёрного тела.
2. Как и в теории
Рэлея и Джинса, рассматривается равновесное тепловое излучение.3. Как и в теории Рэлея и Джинса, считается, что число степеней свободы электромагнитного излучения в полости равно числу стоячих электромагнитных волн, возникающих в полости, умноженному на два.
4. В отличие от теории Рэлея и Джинса, считается, что электромагнитные волны излучаются исключительно порциями – квантами, энергия каждого кванта
5. В отличие от теории Рэлея и Джинса, считается, что вероятность обнаружить колебание с энергией E определяется распределением Больцмана
Это предположение заменило предположение Рэлея и Джинса о равном распределении энергии по степеням свободы.
Nn – число стоячих волн с энергией En.
N – полное число стоячих волн.
(Дж·с).
Слайд 14Среднее значение энергии стоячих волн в полости теперь можно найти
так:
Средняя энергия стоячих волн по Планку.
Энергия одной стоячей волны
Вероятность Pn
определяется распределением Больцмана.Введём обозначение:
Теперь
Слайд 15Это выражение можно преобразовать следующим образом. Предположим, что параметр x
принимает непрерывный ряд значений (а не дискретный, как это происходит
на самом деле). Вычислим производную:Оказалось, производная равна правой части выражения для энергии с точностью до множителя. Поэтому перепишем выражение для средней энергии в виде:
Сумма под знаком логарифма представляет собой геометрическую прогрессию со знаменателем
Слайд 16Знаменатель этой прогрессии
следовательно прогрессия убывает.
Сумма бесконечно убывающей геометрической прогрессии (|q|
равна
где b1 – первый член прогрессии.
Сумма данной бесконечно убывающей геометрической
прогрессии равнаТеперь формулу для средней энергии можно переписать так:
Слайд 17
Вычисляем производную:
Подставляем полученный результат в формулу для средней энергии:
Разделив числитель
и знаменатель на e-x, получим:
Слайд 18Интересно отметить, что полученный результат в классическом пределе, то есть
при h → 0 переходит в классический закон равного распределения
энергии по степеням свободы.При h → 0
Слайд 19Спектральная плотность энергии излучения по Планку.
Как было показано нами ранее,
полное число стоячих волн в полости, окружающей абсолютно чёрное тело,
имеющих частоты в интервале от ω до ω + dωПолное число степеней свободы электромагнитного излучения с частотами в интервале от ω до ω + dω в полости, окружающей абсолютно чёрное тело
Множитель «2» появляется из-за наличия колебаний векторов напряжённости электрического и магнитного полей.
Энергия электромагнитного излучения с частотами в интервале от ω до ω + dω в полости, окружающей абсолютно чёрное тело
Слайд 20
Энергия электромагнитного излучения с частотами в интервале от ω до
ω + dω в полости, окружающей абсолютно чёрное тело
Плотность энергии
электромагнитного излучения с частотами в интервале от ω до ω + dω в полости, окружающей абсолютно чёрное телоПлотность энергии электромагнитного излучения с частотами в интервале от ω до ω + dω в полости, окружающей абсолютно чёрное тело (она же спектральная плотность энергии излучения)
Слайд 21
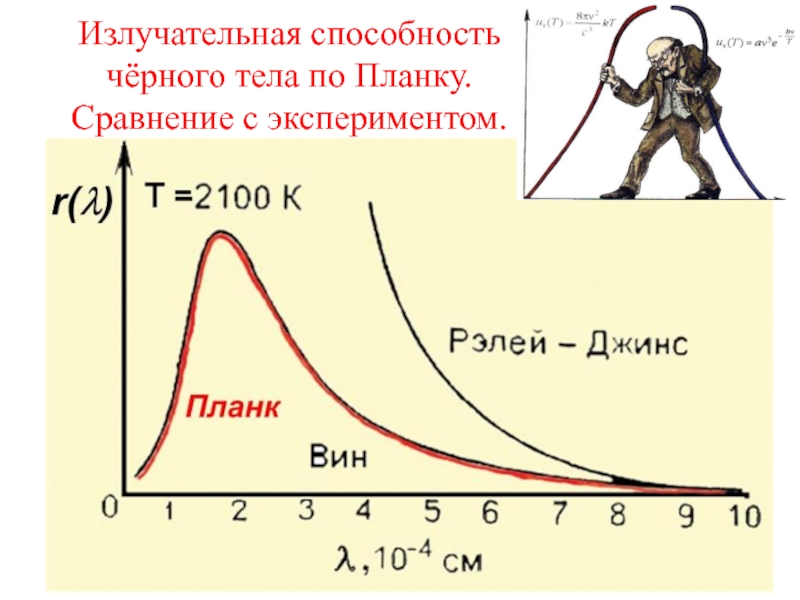
Излучательная способность чёрного тела по Планку.
Как было показано нами ранее,
излучательная способность абсолютно чёрного тела связана со спектральной плотностью излучения
формулойДве последние формулы для спектральной плотности излучения и излучательной способности абсолютно чёрного тела называются формулами Планка.
Слайд 22
Отметим, что при
формула Планка переходит в формулу Рэлея-Джинса.
следовательно,
Для того, чтобы сравнить результаты Планка с экспериментальными данными Вина,
выразим излучательную способность через длину волны.Слайд 24Интегральная энергетическая светимость чёрного тела по Планку.
Интегральная энергетическая светимость чёрного
тела
Подставим в этот интеграл формулу Планка.
Обозначим
Тогда
Этот результат полностью согласуется с
законом Стефана – Больцмана.Слайд 25Вычисление коэффициента σ даёт
(Вт/(м2·К4).
На самом деле, Планк получил значение
постоянной h из условия равенства этого выражения экспериментальному значению постоянной
Стефана – Больцмана.Выводы.
Объяснить закономерности теплового излучения можно лишь использовав два предположения:
электромагнитные волны испускаются порциями – квантами, причём энергия одного кванта равна E = hν;
при подсчёте плотности энергии излучения следует отказаться от закона равного распределения энергии по степеням свободы в пользу применения распределения Больцмана.
Остальные исходные предположения теории равновесного теплового излучения (модель абсолютно чёрного тела, модель равновесного теплового излучения) одинаковы как в классической теории Рэлея и Джинса, так и в квантовой теории излучения Планка.