Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическое моделирование электроэнергетических систем и их элементов
Содержание
- 1. Математическое моделирование электроэнергетических систем и их элементов
- 2. Электрические нагрузкиЭлектрические нагрузки ЭЭС преобразуют электрическую энергию
- 3. К основным электроприемникам в электрической системе относятся:асинхронные двигатели,синхронные двигатели,лампы накаливания,люминесцентные лампы,печи сопротивления.дуговые печи.
- 4. Статические характеристики нагрузкиХарактеристики нагрузки отражают изменение мощности,
- 5. Динамические характеристики нагрузкиАналогичные характеристики, полученные при быстрых
- 6. При малых отклонениях от исходного установившегося режима
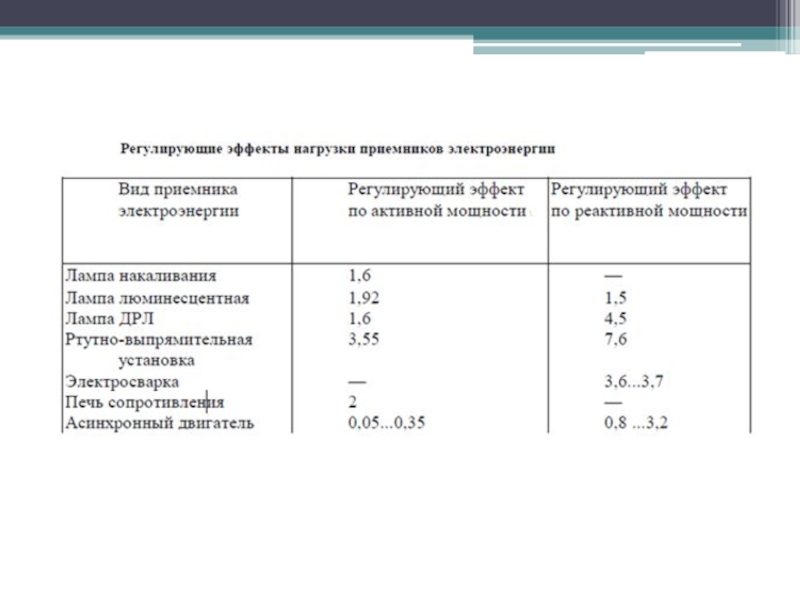
- 7. Регулирующий эффект показывает степень снижения активной и
- 8. Изменения частоты или напряжения связано с некоторыми
- 9. Типовые статические характеристики нагрузкиЗависимости Pн =fp(U), Qн
- 10. Практически приходится пользоваться статическими характеристиками, полученными экспериментально.
- 11. Осветительная нагрузка лампы накаливания, люминесцентные, дуговые ртутные, натриевые, ксеноновые.
- 12. Лампы накаливания Осветительная нагрузка, содержащая лампы накаливания,
- 13. Люминесцентные лампыЛюминесцентные лампы менее чувствительны к отклонениям
- 14. Однако, при снижении напряжения на люминесцентных лампах
- 15. Печи сопротивленияПечи сопротивления имеют характеристики схожие с характеристиками ламп накаливания, но степень напряжения ближе к 2.
- 16. Дуговые печиДуговые печи представляют собой сложную и
- 17. Асинхронные двигателиАсинхронные двигатели. Принцип действия асинхронного двигателя
- 18. Асинхронные двигатели имеют различные статические характеристики Активная
- 19. Реактивная мощность, потребляемая асинхронными двигателями, складывается из:намагничивающей
- 20. При снижении напряжения реактивная мощность рассеяния асинхронных
- 21. Синхронные двигателиВращающееся магнитное поле статора синхронной машины
- 22. Для того, чтобы ротор стал электромагнитом на
- 23. В зависимости от величины тока возбуждения синхронный
- 24. Синхронные двигатели используются как источники реактивной мощности
- 25. Компенсирующие устройстваСинхронные компенсаторы представляют собой синхронные двигатели с облегченным ротором и работающих на холостом ходу
- 26. Статические компенсирующие устройства – реакторы и конденсаторные
- 27. Конденсаторная установкаЕмкостная нагрузка имеет отрицательный регулирующий эффект
- 28. Слайд 28
- 29. Состав типовой нагрузкимелкие асинхронные двигатели 1, крупные
- 30. Для типового состава электроприемников регулирующие эффекты нагрузки по активной и реактивной мощности равны:
- 31. Моделирование электрических нагрузокСтатические характеристики для каждого типа
- 32. Модель 1. Типовые Статические характеристики
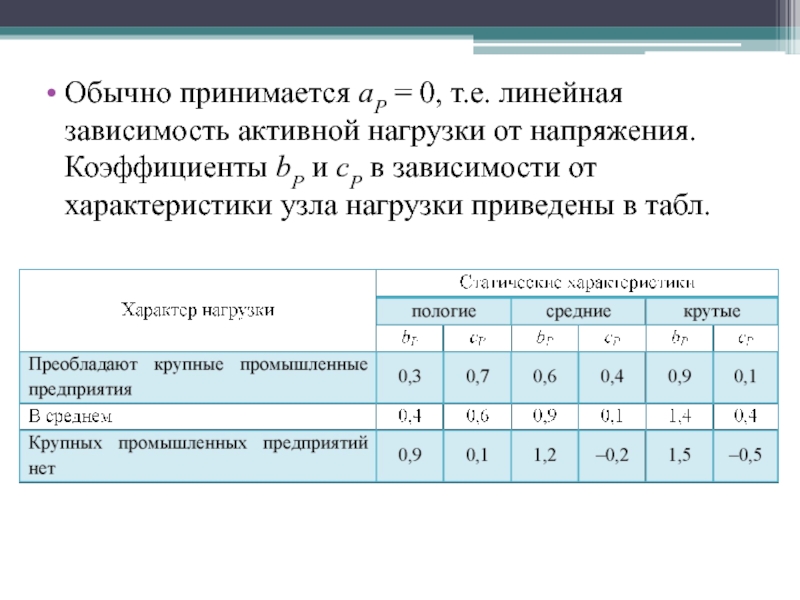
- 33. Обычно принимается aP = 0, т.е. линейная
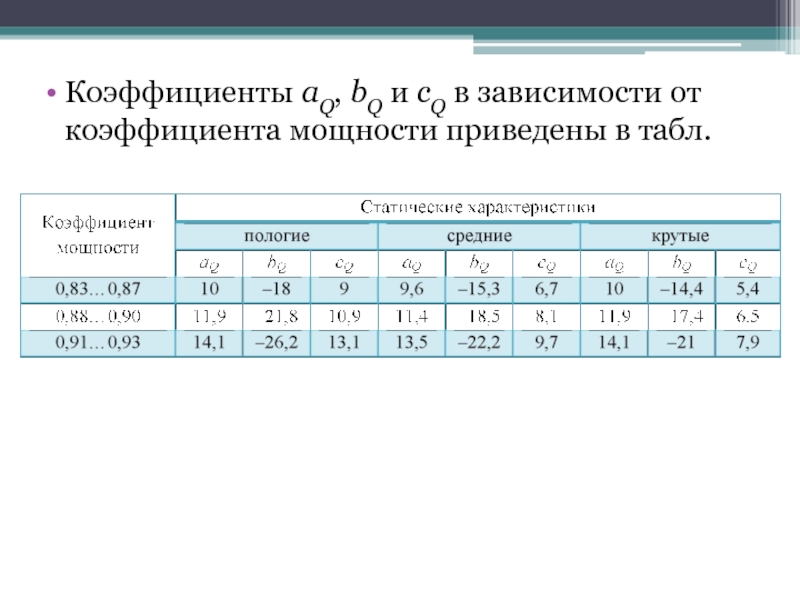
- 34. Коэффициенты aQ, bQ и cQ в зависимости от коэффициента мощности приведены в табл.
- 35. Модель 2. Заданные мощности нагрузокВо многих задачах
- 36. Модель 3. Схемы замещенияРассмотрим электрическую цепь, в
- 37. Даже если считать мощность, потребляемую нагрузкой постоянной, сопротивление будет меняться в зависимости от напряжения по формуле:
- 38. Кроме того, мощность также зависит от напряжения по статической характеристике и поэтому
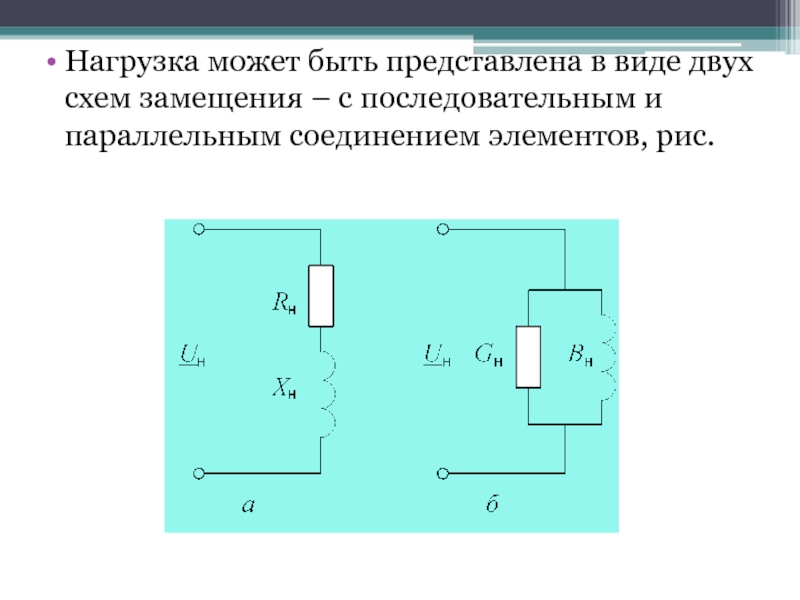
- 39. Нагрузка может быть представлена в виде двух
- 40. При последовательном соединении:а при параллельном:
- 41. При постоянной величине заданного сопротивления или проводимости
- 42. Для активной мощности можно, например, воспользоваться линейной
- 43. На рис. представлены действительные статические характеристики нагрузки
- 44. Модель 4. Заданные токи нагрузкиИногда в качестве
- 45. что дает линейные статические характеристики как активной,
- 46. ПримерНайти коэффициенты математической модели статической характеристики нагрузки
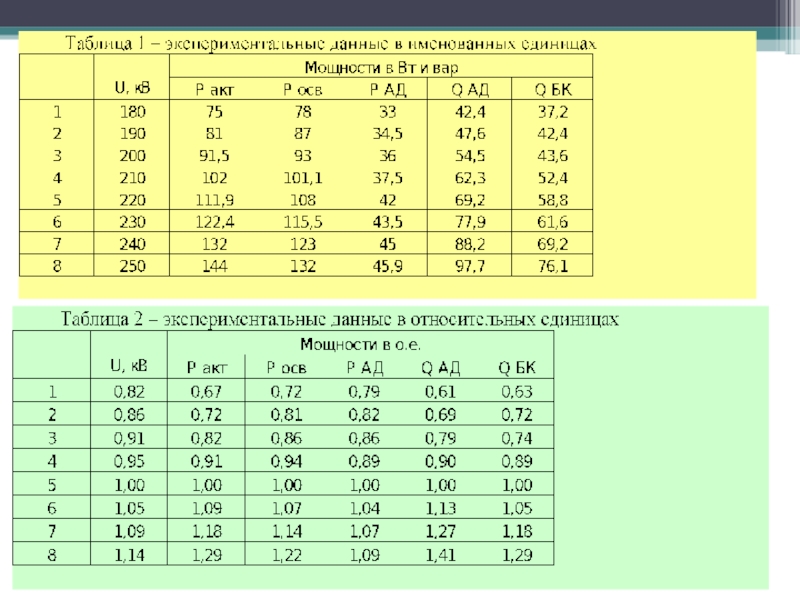
- 47. Все величины приведены в относительных единицах. Исходные данные (результаты эксперимента):
- 48. Коэффициенты функции полиномиальной регрессии:
- 49. Определение функций статических характеристик и аргументов:
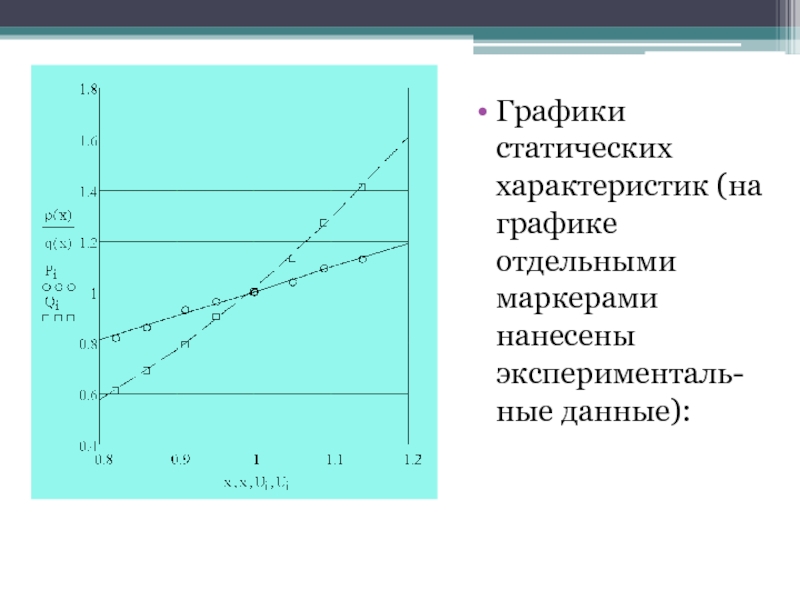
- 50. Графики статических характеристик (на графике отдельными маркерами нанесены эксперименталь-ные данные):
- 51. Регулирующие эффекты:
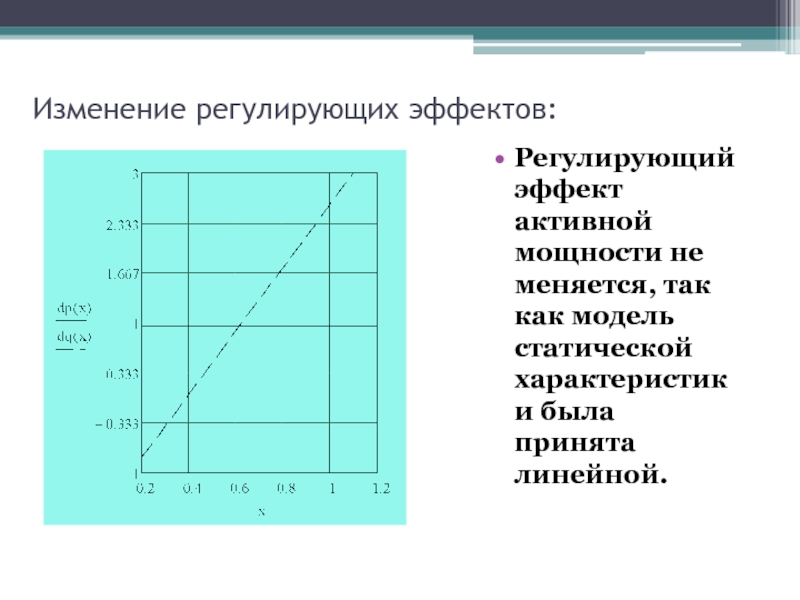
- 52. Изменение регулирующих эффектов:Регулирующий эффект активной мощности не меняется, так как модель статической характеристики была принята линейной.
- 53. Математические модели электрических нагрузок
- 54. Лабораторная работа 7Построение математических моделей нагрузки в
- 55. Задание1. Снять экспериментальные статические характеристики на физической
- 56. 2. Выполнить графическое построение статические характеристики нагрузки
- 57. Описание лабораторного стенда
- 58. Обработка результатов опытовПеревести значения снятых характеристик в
- 59. Оценить среднеквадратическую погрешность аппроксимации всех полученных моделей.Получить
- 60. Слайд 60
- 61. ВыводыДать таблицу погрешностей аппроксимации по всем моделям
- 62. Скачать презентанцию
Электрические нагрузкиЭлектрические нагрузки ЭЭС преобразуют электрическую энергию в другие виды энергии с целью ее дальнейшего использования.Основные виды электрических нагрузок: электродвигатели, осветительная нагрузка, электротранспорт, электропечи.
Слайды и текст этой презентации
Слайд 1Математическое моделирование электроэнергетических систем и их элементов
Лекция 8
Моделирование электрических нагрузок
ЭЭС
Слайд 2Электрические нагрузки
Электрические нагрузки ЭЭС преобразуют электрическую энергию в другие виды
энергии с целью ее дальнейшего использования.
Основные виды электрических нагрузок: электродвигатели,
осветительная нагрузка, электротранспорт, электропечи.
Слайд 3К основным электроприемникам в электрической системе относятся:
асинхронные двигатели,
синхронные двигатели,
лампы накаливания,
люминесцентные
лампы,
печи сопротивления.
дуговые печи.
Слайд 4Статические характеристики нагрузки
Характеристики нагрузки отражают изменение мощности, потребляемой нагрузкой при
изменении подведенного к ней напряжения и частоты.
Характеристики, отвечающие установившемуся режиму
потребителей, называются статическими характеристиками нагрузки: по напряжению [Pн =fp(U), Qн = fq(U)]
и по частоте [Pн = jp(f), Qн =jq (f)].
Слайд 5Динамические характеристики нагрузки
Аналогичные характеристики, полученные при быстрых изменениях напряжения и
частоты в переходном режиме, называются динамическими характеристиками.
Динамические характеристики
Pн =fp(U,t),
Qн = fq(U,t) и соответственно Pн = jp(f,t), Qн =jq (f,t) в отличие от статических характеристик являются функциями времени.
Слайд 6При малых отклонениях от исходного установившегося режима изменение мощности может
быть представлено линеаризованной зависимостью:
где
af, aU и bf, bU
Регулирующие эффекты нагрузки
соответственно активной (a) и реактивной (b)мощности по частоте и напряжению.
Слайд 7Регулирующий эффект показывает степень снижения активной и реактивной нагрузки при
изменении напряжения и частоты.
По статическим характеристикам, построенным в относительных
номинальных единицах, может быть определен регулирующий эффект нагрузки как отношение приращений:
Слайд 8Изменения частоты или напряжения связано с некоторыми процессами в ЭЭС,
которые могут считаться возмущениями.
Регулирующий эффект нагрузки препятствует данным возмущениям
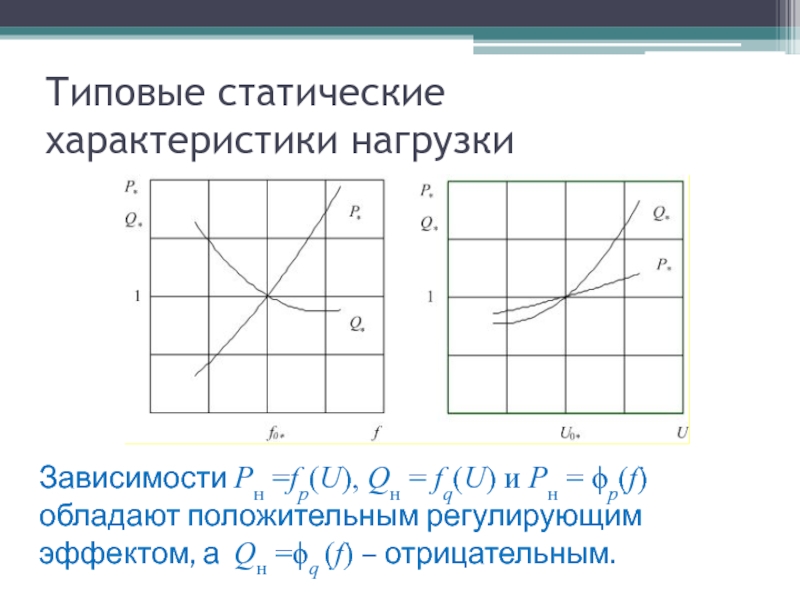
снижая потребляемую мощность нагрузки при уменьшении напряжения или частоты и повышая мощность при их увеличении.
Слайд 9Типовые статические характеристики нагрузки
Зависимости Pн =fp(U), Qн = fq(U) и
Pн = jp(f) обладают положительным регулирующим эффектом, а Qн =jq
(f) – отрицательным.
Слайд 10Практически приходится пользоваться статическими характеристиками, полученными экспериментально.
В некоторых случаях
их удается получить расчетным путем.
В простейшем случае, если известно
сопротивление электроприемника, то статическая характеристика есть квадратичная зависимость от напряжения:
Слайд 11Осветительная нагрузка
лампы накаливания,
люминесцентные,
дуговые ртутные,
натриевые,
ксеноновые.
Слайд 12Лампы накаливания
Осветительная нагрузка, содержащая лампы накаливания, примерно пропорциональна напряжению
в степени 1,6. Реактивную мощность такая нагрузка не потребляет.
Слайд 13Люминесцентные лампы
Люминесцентные лампы менее чувствительны к отклонениям напряжения.
При повышении напряжения
потребляемая мощность и световой поток увеличиваются, а при снижении –
уменьшаются, но не в такой степени как у ламп накаливания.
Слайд 14Однако, при снижении напряжения на люминесцентных лампах до величины 0,9Uном
они начинают мерцать, а при величине напряжения 0,8Uном просто не
загораются.Регулирующий эффект люминесцентных ламп по схеме с расщепленной фазой равен примерно 1,9 для активной мощности, а для реактивной мощности может быть оценен величиной 1,5.
Слайд 15Печи сопротивления
Печи сопротивления имеют характеристики схожие с характеристиками ламп накаливания,
но степень напряжения ближе к 2.
Слайд 16Дуговые печи
Дуговые печи представляют собой сложную и тяжелую нагрузку для
энергосети – это крупный, несимметричный и в высокой степени нестабильный
потребитель по реактивной мощности.Активная мощность, потребляемая печью, меняется пропорционально квадрату напряжения.
Слайд 17Асинхронные двигатели
Асинхронные двигатели. Принцип действия асинхронного двигателя основан на явлении
электромагнитной индукции.
В неподвижную трехфазную обмотку статора асинхронного двигателя подается
переменный ток, который формирует в статоре вращающееся магнитное поле. Это поле пересекает проводники замкнутой обмотки ротора и наводит в них ЭДС, под действием которых по обмотке ротора будет протекать ток.
Взаимодействие этого тока с полем статора создает на проводниках обмотки ротора электромагнитные силы – вращающий момент, направление которого определяется по правилу «левой руки».
Эти силы увлекают ротор в сторону вращения магнитного потока.
Скорость вращения ротора всегда меньше скорости вращения магнитного поля статора.
Слайд 18Асинхронные двигатели имеют различные статические характеристики
Активная мощность в сильной
мере зависит от мощностей машин, приводимых во вращение двигателями.
Реактивная
мощность имеет разную зависимость от напряжения в зависимости от номинальной мощности двигателя. Маломощные двигатели имеют более крутые характеристики по сравнению с мощными двигателями.
Слайд 19Реактивная мощность, потребляемая асинхронными двигателями, складывается из:
намагничивающей мощности, связанной с
намагничивающим током, и
мощности рассеяния, связанной с созданием полей рассеяния
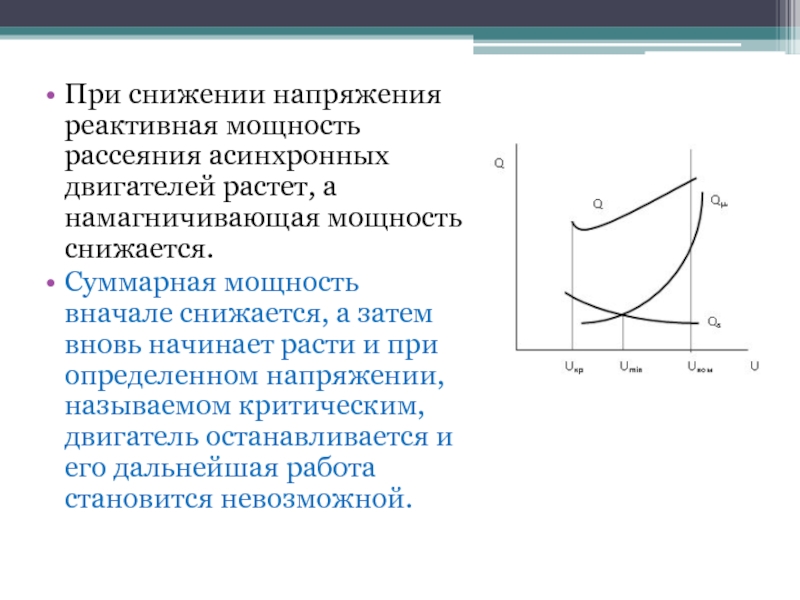
в статоре и роторе. 
Слайд 20При снижении напряжения реактивная мощность рассеяния асинхронных двигателей растет, а
намагничивающая мощность снижается.
Суммарная мощность вначале снижается, а затем вновь
начинает расти и при определенном напряжении, называемом критическим, двигатель останавливается и его дальнейшая работа становится невозможной.
Слайд 21Синхронные двигатели
Вращающееся магнитное поле статора синхронной машины увлекает за собой
ротор, который является электромагнитом – индуктором.
Разноименные полюса магнитного поля
статора и ротора притягиваются и ротор вращается с постоянной скоростью. 
Слайд 22Для того, чтобы ротор стал электромагнитом на него подается постоянный
ток – ток возбуждения.
Этот ток при вращении ротора вызывает
магнитное поле в статоре – реакцию якоря. 
Слайд 23В зависимости от величины тока возбуждения синхронный двигатель может работать
в режиме перевозбуждения или недовозбуждения.
Режим перевозбуждения – это нормальный
режим работы двигателя. Мощные синхронные двигатели изготавливают с номинальным коэффициентом мощности 0,9 и 0,8 при работе с перевозбуждением.
Слайд 24Синхронные двигатели используются как источники реактивной мощности в ЭЭС и
применяются для регулирования напряжения.
Ток возбуждения синхронных машин изменяется в
соответствии с законом регулирования напряжения в сети, поэтому его статические характеристики по реактивной мощности зависят от закона регулирования напряжения в узле нагрузки, к которому он присоединен. В целом синхронные двигатели имеют положительный регулирующий эффект как по активной, так и по реактивной мощности.
Слайд 25Компенсирующие устройства
Синхронные компенсаторы представляют собой синхронные двигатели с облегченным ротором
и работающих на холостом ходу
Слайд 26Статические компенсирующие устройства – реакторы и конденсаторные установки
Индуктивная и емкостная
нагрузка имеют квадратичные зависимости реактивной мощности от напряжения.
Сухие реакторы
Слайд 29Состав типовой нагрузки
мелкие асинхронные двигатели 1,
крупные асинхронные двигатели 2,
освещение 3,
выпрямители, инверторы, печи и нагревательные приборы 4,
синхронные
двигатели 5, потери в сети 6.
Слайд 30Для типового состава электроприемников регулирующие эффекты нагрузки по активной и
реактивной мощности равны:
Слайд 31Моделирование электрических нагрузок
Статические характеристики для каждого типа электрической нагрузки и
их совокупностей могут быть получены экспериментально.
Однако в каждом конкретном
случае это затруднительно и чаще всего пользуются так называемыми типовыми характеристиками.
Слайд 33Обычно принимается aP = 0, т.е. линейная зависимость активной нагрузки
от напряжения. Коэффициенты bP и cP в зависимости от характеристики
узла нагрузки приведены в табл.
Слайд 35Модель 2. Заданные мощности нагрузок
Во многих задачах удобной пользоваться самой
простой моделью нагрузки:
Pн = const; Qн = const.
Это допустимо в
проектных задачах и в сетях высокого напряжения, в которых используются средства регулирования напряжения на шинах нагрузки.
Слайд 36Модель 3. Схемы замещения
Рассмотрим электрическую цепь, в которой имеется нагрузка,
представленная в виде сопротивления Zн. Это сопротивление в общем случае
является переменной величиной – получается нелинейная электрическая цепь.
Слайд 37Даже если считать мощность, потребляемую нагрузкой постоянной, сопротивление будет меняться
в зависимости от напряжения по формуле:
Слайд 39Нагрузка может быть представлена в виде двух схем замещения –
с последовательным и параллельным соединением элементов, рис.
Слайд 41При постоянной величине заданного сопротивления или проводимости моделирование с помощью
вышеприведенных выражений дает характеристики:
т.е. квадратичная зависимость активной и реактивной мощности
от напряжения. Такая модель для реактивной мощности вполне приемлема.
Слайд 42Для активной мощности можно, например, воспользоваться линейной моделью, тогда будем
иметь:
где Gн и Bн вычислены при номинальном напряжении нагрузки.
Слайд 43На рис. представлены действительные статические характеристики нагрузки – сплошные линии
и характеристики, полученные по схемам замещения– пунктирные линии.
Слайд 44Модель 4. Заданные токи нагрузки
Иногда в качестве данных по нагрузке
бывают известны измеренные токи нагрузки. Принимая какое либо значение коэффициента
мощности нагрузки, ее можно моделировать постоянными значениями токов Iн:
Слайд 45что дает линейные статические характеристики как активной, так и реактивной
мощности. Такие модели нагрузки используются в низковольтных сетях
Слайд 46Пример
Найти коэффициенты математической модели статической характеристики нагрузки по опытным данным
для активной и реактивной мощности и определить их регулирующие эффекты.
Используем линейную модель для активной мощности и параболу для реактивной мощности. Построение характеристик выполним в Mathcad.
Слайд 50Графики статических характеристик (на графике отдельными маркерами нанесены эксперименталь-ные данные):
Слайд 52Изменение регулирующих эффектов:
Регулирующий эффект активной мощности не меняется, так как
модель статической характеристики была принята линейной.
Слайд 54Лабораторная работа 7
Построение математических моделей нагрузки в электрических сетях
Цель
работы: Освоить методику получения экспериментальных характеристик электрической нагрузки и научиться
строить математические модели путем обработки экспериментальных данных на основе приближения функций.
Слайд 55Задание
1. Снять экспериментальные статические характеристики на физической модели:
а) для активной
нагрузки (нагревательный элемент);
б) осветительной нагрузки (лампы накаливания);
в) емкостной нагрузки;
г) асинхронного
двигателя;д) узла нагрузки без емкости;
е) узла нагрузки с емкостью.
Слайд 562. Выполнить графическое построение статические характеристики нагрузки в относительных единицах
при номинальных условиях.
3. Построить математические модели статических характеристик нагрузки в
виде степенных и полиномиальных функций, определить для них регулирующие эффекты и сравнить с теоретическими 
Слайд 58Обработка результатов опытов
Перевести значения снятых характеристик в относительные единицы. За
базисные значения принять номинальное напряжение 220 В и мощность, соответствующую
этому напряжению.Аппроксимировать полученные зависимости полиномом второй степени. Для ламп накаливания использовать также степенную функцию.
Сравнить полученные модели для активной нагрузки, ламп накаливания и емкостной нагрузки с моделью квадратичной функции (параболы). Сопротивление нагрузки принять равным единице при номинальных значениях напряжения и мощности.
Слайд 59Оценить среднеквадратическую погрешность аппроксимации всех полученных моделей.
Получить функции регулирующих эффектов
для всех полученных статических характеристик.
Сделать выводы об адекватности полученных
моделей.
Слайд 61Выводы
Дать таблицу погрешностей аппроксимации по всем моделям статических нагрузок.
Дать сравнительную
характеристику квадратичной модели и степенной функции для осветительной нагрузки.
Привести значения
регулирующих эффектов и их ранжировку.
