Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Relational Calculus
Содержание
- 1. Relational Calculus
- 2. CONTENTSRelational calculus (tuple, domain)Codd calculusALPHA language Equivalence and completenessExamples
- 3. Set theory and logicSet theory
- 4. Relational calculusSubset of formulas of the predicate
- 5. Tuple relational calculus (TRC)Query (in simple case)
- 6. TRC – basic componentsConstants: 7, 'john', 3.14159
- 7. TRC – Well formed formulas Atomic formulas:
- 8. TRC – Free and bound variables. Queries.The
- 9. Example of DB for queries in TRCFAC
- 10. TRC – Examples of projection, selection
- 11. TRC – Examples of existential quantifiers{(f.Name,d.Name) |
- 12. TRC – Examples of universal quantifiersQuery. Output
- 13. TRC - Save formulas and queriesExist such
- 14. Restricted variablesTuple variable is restricted if it
- 15. Restricted logical connectivesIf two formulas F and
- 16. Restricted quantifiersПримеры: ∃x(x.Fund < 5) – existential quantifier
- 17. Domain Relational Calculus (DRC)Query has the form
- 18. Example of queries in DRC1) ProjectionQuery. Output
- 19. Equivalence of RA, TRC, DRC and
- 20. Codd relational calculus (СRС)CRC is subset of
- 21. CRC – basic components Constants: 7, 'john',
- 22. CRC – well formed formulasTerms: P.t –
- 23. Formula well defined over quantifiersAs a matter
- 24. Formula with domain of definition Formula W
- 25. Alpha expressionExpression (t1, t2,…, tk) : W
- 26. ALPHA languageSimplified syntax: RANGE [ SOME
- 27. Example of queries in ALPHA and CRCQuery.
- 28. SummaryRelational calculus is declarative (not procedural) language
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Lecture 7. Relational calculus
National Aviation University
Computer Science Faculty
Department of Software
Engineering
Слайд 2CONTENTS
Relational calculus (tuple, domain)
Codd calculus
ALPHA language
Equivalence and completeness
Examples
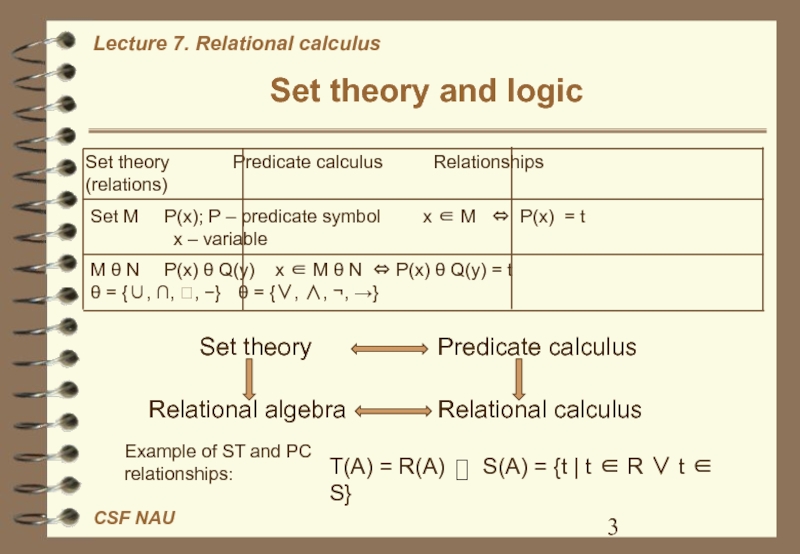
Слайд 3Set theory and logic
Set theory Predicate calculus
Relationships
(relations)
Set М Р(х); Р – predicate symbol
х ∈ М ⇔ Р(х) = t
х – variableМ θ N Р(х) θ Q(y) х ∈ М θ N ⇔ Р(х) θ Q(y) = t θ = {∪, ∩, , −} θ = {∨, ∧, ¬, →}
Set theory
Predicate calculus
Relational algebra
Relational calculus
Example of ST and PC relationships:
Слайд 4Relational calculus
Subset of formulas of the predicate calculus
Formal description of
WHAT it is necessary to select from DB.
Example:
NL - “Output
faculties with Fund > 10000"RL - {t | (FAC(t) & t.fund > 10000}
It has possibility of query languages but does not have data manipulation possibilities (just the same as relational algebra)
Two variants of relational calculus:
Tuple relational calculus (TRC) – variables represent rows of relations
Domain relational calculus (DRC) - variables represent domains of attributes of relations
Слайд 5Tuple relational calculus (TRC)
Query (in simple case) has the form
{t | (F(t)}
t - tuple variable;
F(t) – formula that contains
tuple variable tAnswer. Is the set of all tuples t for which the formula F(t) evaluates to true.
Formula. It is recursively defined from simple atomic formulas (get tuples from relations or make comparison of values) and build more complex formulas using the logical connectives and quintifiers.
SQL. It is formal foundation of SQL language.
Слайд 6TRC – basic components
Constants: 7, 'john', 3.14159 and so on.
Tuple
variables: t1, t2,... –
They are interpreted by relation tuples.
Projection
of tuple variables: t.a,…
а – attribute name. Predicate symbols: P, P1,...,Q, Q1,… They are interpreted by relations
Comparison operators (predicates) : = {=, <, <=, >, >=, <>} и т.д.
Logical connectives: ∨ (or), ∧(&) (and), ¬ (not), → (implies)
Quantifiers: ∃(exists), ∀(for all)
Слайд 7TRC – Well formed formulas
Atomic formulas:
P(t) - P
– predicate symbol, - t - tuple variable.
If Р interpreted by relation R then P(t) means t ∈ Rt.a θ t.b - t.a and t.b – tuple projections
t.a θ с - t.a – tuple projection, с - constant
Well formed formulas (wff):
Atomic formulas are wff;
If F is wff then ¬F and (F) are wff
If F and G are wff then F ∨ G, F ∧ G, F → G are wff
If F is wff with free variable t then ∃tF(t) and ∀tF(t) are wff with bound variable t.
Слайд 8TRC – Free and bound variables. Queries.
The use of quantifiers
∃tF(t) and ∀tF(t) in any formula is said to bind
t in the formula F. A variable that is not bound is free.Query – in general case it is espression:
{(t1,t2,...) | (F(t1,t2,...)}
where - t1,t2,... - tuple variables or their projections;
- F(t1,t2,...) - formula that contains free tuple variables t1,t2,...
IMPOPRTANT RESTRICTION: The variable t1,t2,..., that appears to the left of ’|’, must be the only free variables in the formula F. In other words all other tuple variables of the formula F must be bound by using quantifiers.
Слайд 9Example of DB for queries in TRC
FAC FACULTY (FNo, Name,
Dean, Bld, Fund)
DEP DEPARTMENT (DNo, FNo, Name, Head, Bld, Fund)
TCH TEACHER(TNo, DNo, Name, Post, Tel, Salary, Comm)
GRP GROUP(GNo, DNo, Course, Num, Quantity, CurNo)
SBJ SUBJECT(SNo, Name)
ROM ROOM (RNo, Num, Building, Seats)
LEC LECTURE (TNo, GNo, SNo, RNo, Type, Day, Week)
Predicate symbols
Relations of database
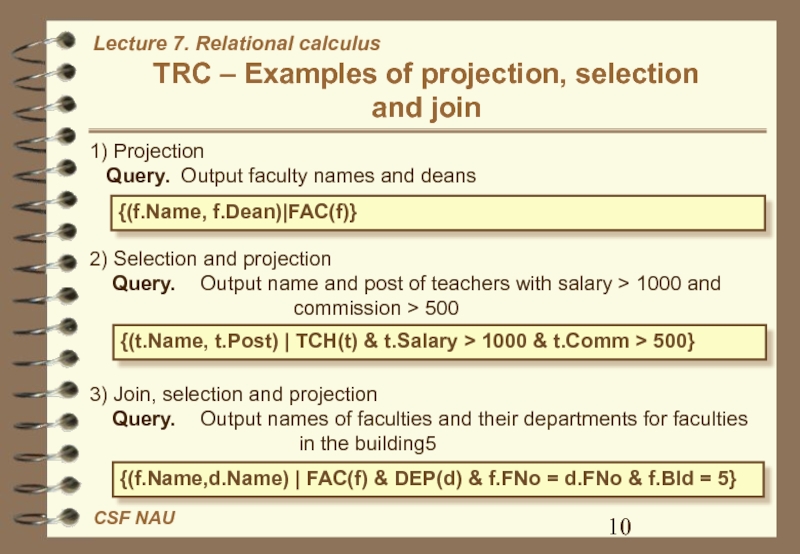
Слайд 10TRC – Examples of projection, selection
and join
1) Projection
Query. Output faculty names and deans
2) Selection and projection
Query. Output name and post of teachers with salary > 1000 and
commission > 500{(f.Name, f.Dean)|FAC(f)}
3) Join, selection and projection
Query. Output names of faculties and their departments for faculties
in the building5
{(t.Name, t.Post) | TCH(t) & t.Salary > 1000 & t.Comm > 500}
{(f.Name,d.Name) | FAC(f) & DEP(d) & f.FNo = d.FNo & f.Bld = 5}
Слайд 11TRC – Examples of existential quantifiers
{(f.Name,d.Name) | DEP(d) & FAC(f)
& f.FNo = d.FNo & f.Bld = 5}
Query. Output department
names of faculties in the building 5{d.Name | DEP(d) & ∃f(FAC(f) & f.FNo = d.FNo & f.Buld = 5)}
Query. Outputs names of teacher-professors that have lectures in groups of the 1-st course
{t.Name | TCH(t) & t.Post='professor' &
∃l(LEC(l) & l.TNo = t.Tno &
∃g(GRP(g) & l.GNo = g.GNo & g.Course = 1))}
Output names of professors,
for which exist such lectures,
for which (lectures) exist groups of the 1-st course
Query. Output names of faculties in the building 5 and their departments
Слайд 12TRC – Examples of universal quantifiers
Query. Output numbers of the
teachers that have lectures in all groups
{l.TNo | LEC(l) &
∀g(GRP(g) → g.GNo = l.GNo)}Query. Output numbers of the teachers that have lectures in all groups of the 1-st course.
{l.TNo | LEC(l) & ∀g((GRP(g) & g.Course = 1) → g.GNo = l.GNo)}
Query. Output names of the teachers that have lectures in all groups of the
1-st course
{t.Name | TCH(t) & ∃l(LEC(l) & l.TNo = t.TNo &
∀g((GRP(g) & g.Course = 1) → g.GNo = l.GNo)}
Output names of teachers,
that have such lectures,
that are taught in all groups of the 1-st course
Слайд 13TRC - Save formulas and queries
Exist such syntactically correct queries
that do not have correct interpretation in DB. OR, other
words, such queries have an infinite number of answers (answer is infinite relation). Such queries are called unsafe Examples:Query is safe if it is interpreted by a finite relation.
Query is safe if:
All variables in the formula are restricted;
All logical connectives in the formula are restricted;
All quantifiers in the formula are restricted.
{t | t.Post = 'professor'}
{t | ¬TCH(t)}
{(t,d) | TCH(t) ∨ DEP(d)}
Слайд 14Restricted variables
Tuple variable is restricted if it belongs to any
predicate that is interpreted by DB relation, or it is
restricted by other restricted variable or constant.Variable t is restricted if :
It belongs to a predicate Р(t), where Р is interpreted by DB relation;
It appears in the formula t.a1 = c1 & ... & t.an = cn, where
a1,..., an are all attributes of the tuple t, and c1, ..., cn are constants;
It appears in the formula t = s, where s is restricted variable.
Examples:
P(t) - variable t is restricted by the predicate P
P(t) & t = x - variable x is restricted by variable t that is restricted itself
t.Name=‘john’ & t.Post=‘prof’ & t.Salary = ‘1200’
Слайд 15Restricted logical connectives
If two formulas F and G have restricted
variables then:
F ∨ G is a formula with restricted variables
if F and G have the same
free variables;F & G will always be the formula with restricted variables in spite of the list of free variables in both formulas;
F & ¬G is the formula with restricted variables if F and G have the same free variables;
F → G will never be a formula with restricted varibles.
Examples:
P(t) ∨ Q(t) – it is formula with restricted variable
P(t) ∨ Q(q) – variables in this formula are not restricted
P(t) & Q(q) – it is formula with restricted variable
¬Q(t) – it is not formula with restricted variable
P(t) & ¬Q(q) – it is not formula with restricted variables
P(t) & ¬Q(t) – it is formula with restricted variable
Слайд 16Restricted quantifiers
Примеры:
∃x(x.Fund < 5) – existential quantifier is not restricted
∃x(P(x)
& x.Fund < 5) – existential quantifier is restricted
∀x(P(x)) →
Q(x, y)) – universal quantifier is restrictedIf F(t) is restricted formula and G(t) is arbitrary formula then the formula ∃t(F(t)& G(t)) is a formula with restricted existential quantifier. This formula is interpreted by restricted (finite) relation.
If F(t) is restricted formula and G(t) is arbitrary formula then the formula ∀t(F(t) → G(t)) is a formula with restricted universal quantifier. This formula is interpreted by restricted (finite) relation.
Слайд 17Domain Relational Calculus (DRC)
Query has the form {x1,x2,...,xn | (F(x1,x2,...,xn)}
x1,x2,...,xn
- attributes domain variables;
F(x1,x2,...,xn) – a formula with the only
free
variables x1,x2,...,xn
Answer. Set of such tuples
Formula. It is recursively defined by using atomic formulas and more complex formulas with the help of logical connectives and quantifiers just the same as in tuple relational calculus. Safe formulas are defined just the same as in tuple relational calculus.
QBE. Is a formal base of QBE language.
Слайд 18Example of queries in DRC
1) Projection
Query. Output faculty names and
deans
{(y, z)|∃x∃u∃vFAC(x,y,z,u,v)}
2) Selection and projection
Query. Output faculty names of
the building 5 and dean names{(y, z) | ∃x∃u∃vFAC(x,y,z,u,v) & u = 5}
3) Join, selection and projection
Query. Output faculty names of the building 5 and their department names
{(y,n)|∃x∃f(∃z∃u∃v(FAC(x,y,z,u,v) & u=5) & ∃d∃h∃b∃uDEP(d,f,n,h,b,u) & x=f)}
FAC (FNo,Name,Dean,Bld,Fund) DEP(DNo,FNo,Name,Head,Bld,Fund)
x y z u v d f n h b u
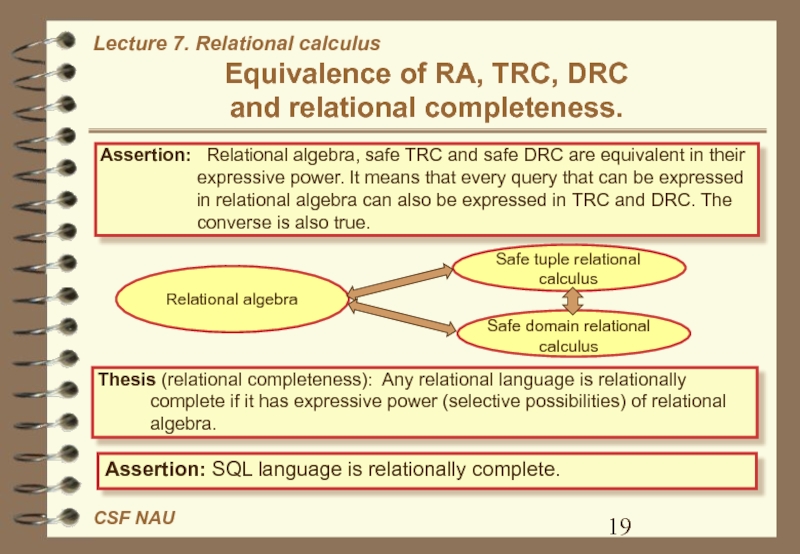
Слайд 19
Equivalence of RA, TRC, DRC
and relational completeness.
Thesis (relational
completeness): Any relational language is relationally complete if it has
expressive power (selective possibilities) of relational algebra. Assertion: Relational algebra, safe TRC and safe DRC are equivalent in their expressive power. It means that every query that can be expressed in relational algebra can also be expressed in TRC and DRC. The converse is also true.
Relational algebra
Safe tuple relational calculus
Safe domain relational calculus
Assertion: SQL language is relationally complete.
Слайд 20Codd relational calculus (СRС)
CRC is subset of the predicate calculus
(of the 1-st order)
It is tuple oriented
It solve differences between
wff and safe formulasCRC queries are safe.
It is equivalent to the relational algebra; it means that CRC is relationally complete
Слайд 21CRC – basic components
Constants: 7, 'john', 3.14159 and so
on.
Tuple variables: t1, t2,... –
They are interpreted by relation
tuples.Projections of tuple variables: t.[i],… i is a component of tuple variable.
Predicate symbols: P, P1,...,Q, Q1,… They are interpreted by relations
Comparison operators (predicates): = {=, <, <=, >, >=, <>} и т.д.
Logical connectives: ∨ (or), ∧(&) (and), ¬ (not ), → (implies)
Quantifiers: ∃(exist), ∀(for all)
Слайд 22CRC – well formed formulas
Terms:
P.t – value term:
P - predicate, t - tuple variable.
If Р is interpreted by relation R, then P.t means t ∈ Rt[i] θ s[j], t[i] = c - join term
Examples: t1[3] = t2[1]; t4[7] = 15
Formula well defined over tuple variable:
All predicate symbols is interpreted by relations that are union compatible .
This formula contains only value terms with the only tuple variable.
Value terms are connected by logical operands ∨, &, ¬. More over, operand ¬ directly preceded by operand &.
Examples:
P1.t ∨ P2.t ∨ (P3.t & P4.t); (P1.t ∨ P2.t) & ¬P3.t.
Слайд 23Formula well defined over quantifiers
As a matter of fact, it
is a special case of the restricted existence and universal
quantifiers. Formula F determines interpretation domain of the variable that is used quantifies. We also will use the following notation on these formulas:∃F(G) и ∀F(G)
Lets F is a formula well defined over tuple variable t, а G is a formula that contains t as a free variable, but does not contains value terms of the form P.t. Then formulas:
∃t(F & G); ∀t(F → G)
are called well defined over existence and universal quantifies.
Examples:
∃t((P.t ∨ Q.t) & ¬S.t) & t[2] = ‘john’ & t[5] = 1000)
∀t((P.t ∨ Q.t) & ¬S.t) → (t[2] = ‘john’ & t[5] = 1000))
Слайд 24Formula with domain of definition
Formula W refers to as
formula with domain of definition if it
has the following
expression :W = U1 & U2 &…& Un & V, n ≥ 1
and has the following properties:
Each formula Ui is well defined over tuple variable ti.
Formula V is empty or has the following properties:
If the are quantifies then they are well defined .
Each free variable from V belongs to one of the variables of formulas U1, U2,…, Un
В Formula V does not have value terms with free variables.
Examples: P.r & Q.s & R.t - Cartesian product
P.r & (r[3] = b) - selection
P.r & Q.s & (r [2] = s[1]) - join
Слайд 25Alpha expression
Expression (t1, t2,…, tk) : W is calles simple
alpha expression if it has the following priperties:
W is a
formula with domain of definition. t1, t2,…, tk – list of tuple variables and their projections. These variables must be free in the formula W.
Arbitrary alpha expression is defined recursively in such a way:
Every simple alpha expression is alpha expression .
Let us t = (t1, t2,…, tk). If t : W1 и t : W2 is alpha expression then expressions t : W1 ∨ W2, t : W1 & W2 and t : W1 & ¬W2 are alpha expressions.
Слайд 26ALPHA language
Simplified syntax:
RANGE [ SOME |
ALL]
…
GET ( ) :
range – it shows
name of the the tuple variable SOME | ALL – is it necessary to interpret variable with existential or universal quantifier?
workspace – it is name of temporary work relation that contains result of executing of GET command.
target list – target list of tuple variables and their projections; they show columns that are projected into the resulting relation.
wff – well wormed formula of the tuple relational calculus
Слайд 27Example of queries in ALPHA and CRC
Query. Output names of
faculties and their deans
CRC: {f[2], f[3] | FAC.f}
ALPHA: RANGE FACULTY f
GET W(f.Name,
f.Dean)Query. Output dean name of the CSF faculty
CRC: {f[3] | FAC.f & f[2] = ‘CSF’}
ALPHA: RANGE FACULTY f
GET W(f.Dean) : f.Name = ‘CSF’
Query. Output department names of the CSF faculty
CRC: {d[3] | DEP.d & ∃f(FAC.f & f[2] = ‘CSF’ & f[1] = d[2])}
ALPHA: RANGE FACULTY f SOME
RANGE DEPARTMENT d
GET W(d.Name) = f.Name = ‘CSF’ & f.FNo = d.DNo
Слайд 28Summary
Relational calculus is declarative (not procedural) language that
formulates WHAT
it is necessary to receive but not HOW the result
should be calculated.Safe relational calculus (TRC, DRC, CRC) and relational algebra have the same expressive power and they are used to formulate thesis about relational completeness.
It is possible to formulate correct but not effective queries. So it is necessary to use optimizers.
There are languages that implement relational calculus in straight a way (ALPHA, QUEL) and are also based on the tuple calculus (SQL) and the domain calculus (QBE).






















![Relational Calculus ALPHA languageSimplified syntax: RANGE [ SOME | ALL] …GET ( ALPHA languageSimplified syntax: RANGE [ SOME | ALL] …GET ( ) : range – it shows name of](/img/thumbs/2b9955999d2e135b6bcccdfb424f324f-800x.jpg)
![Relational Calculus Example of queries in ALPHA and CRCQuery. Output names of faculties Example of queries in ALPHA and CRCQuery. Output names of faculties and their deansCRC: {f[2], f[3] | FAC.f}ALPHA: RANGE](/img/thumbs/93f64be7d6f1d037e3ce55b1940029b2-800x.jpg)