Слайд 2Работа по решению любой задачи с использованием компьютера делится на
следующие этапы:
Постановка задачи.
Формализация задачи.
Построение алгоритма.
Составление программы на языке программирования.
Отладка и
тестирование программы.
Проведение расчетов и анализ полученных результатов.
Слайд 3Таким образом, программист должен обладать следующими знаниями и навыками:
• уметь
строить алгоритмы;
• знать языки программирования;
• уметь работать в соответствующей системе
программирования.
Слайд 4Понятие алгоритма
Одним из фундаментальных понятий в информатике является понятие алгоритма.
Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит
от Algorithm! — латинского написания имени Мухаммеда аль-Хорезми (787—850), выдающегося математика средневекового Востока.
Слайд 5Алгоритм — это последовательность команд управления каким-либо исполнителем.
В школьном
курсе информатики с понятием алгоритма, с методами построения алгоритмов ученики
знакомятся на примерах учебных исполнителей: Робота, Черепахи, Чертежника и т.д. Эти исполнители ничего не вычисляют. Они создают рисунки на экране, перемещаются в лабиринтах, перетаскивают предметы с места на место. Таких исполнителей принято называть исполнителями, работающими в обстановке.
Слайд 6В разделе информатики под названием «Программирование» изучаются методы программного управления
работой ЭВМ. Следовательно, в качестве исполнителя выступает компьютер. Компьютер работает
с величинами — различными информационными объектами: числами, символами, кодами и т. п. Поэтому алгоритмы, предназначенные для управления компьютером, принято называть алгоритмами работы с величинами.
Слайд 7Данные и величины
Совокупность величин, с которыми работает компьютер, принято называть
данными. По отношению к программе данные делятся на исходные, результаты
(окончательные данные) и промежуточные, которые получаются в процессе вычислений.
исходные
промежуточные
результат
Слайд 8Пример
при решении квадратного уравнения
ax2 + bx + с =
0
исходными данными являются коэффициенты а, b, с, результатами —
корни уравнения х1, х2, промежуточным данным — дискриминант уравнения D = b2 — 4aс.
Слайд 9Для успешного освоения программирования необходимо усвоить следующее правило: всякая величина
занимает свое определенное место в памяти компьютера (иногда говорят —
ячейку памяти).
Слайд 10У всякой величины имеются три основных свойства: имя, значение и
тип.
В алгоритмах и языках программирования величины делятся на константы и
переменные.
Слайд 11Константа — неизменная величина, и в алгоритме она представляется собственным
значением, например: 15, 34.7, k, true и т.д. Переменные величины
могут изменять свои значения в ходе выполнения программы и представляются символическими именами — идентификаторами, например: X, S2, codl5. Любая константа, как и переменная, занимает ячейку памяти, а значение этих величин определяется двоичным кодом в этой ячейке.
Слайд 12типы величин — типы данных
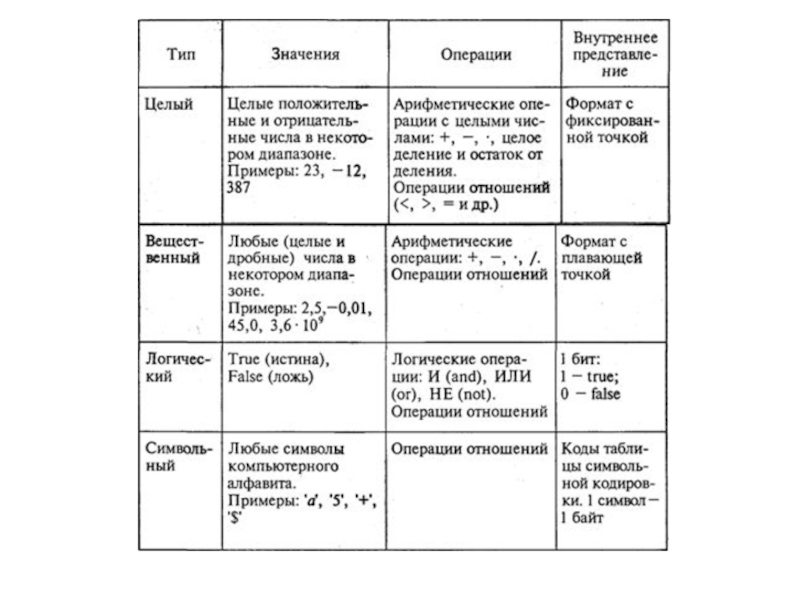
В любой язык входит минимально необходимый
набор основных типов данных, к которому относятся: целый, вещественный, логический
и символьный типы. С типом величины связаны три ее характеристики: множество допустимых значений, множество допустимых операций, форма внутреннего представления
Слайд 14Есть еще один вариант классификации данных — классификация по структуре.
Данные делятся на простые и структурированные. Для простых величин (их
еще называют скалярными) справедливо утверждение: одна величина — одно значение, для структурированных: одна величина — множество значений. К структурированным величинам относятся массивы, строки, множества и т.д.
Слайд 15Компьютер— исполнитель алгоритмов
Исполнителем является комплекс компьютера + Система программирования (СП).
Программист составляет программу на том языке, на который ориентирована СП.
Например, компьютер с работающей системой программирования на Бэйсике называют Бэйсик-машиной; компьютер с работающей системой программирования на Паскале называют Паскаль-машиной и т.п.
Слайд 16Независимо от того, на каком языке программирования будет написана программа,
алгоритм решения любой задачи на компьютере может быть составлен из
команд:
• присваивания;
• ввода;
• вывода;
• обращения к вспомогательному алгоритму;
• цикла;
• ветвления.
Слайд 17
Линейные вычислительные алгоритмы
Рассмотрим пример.
В школьном учебнике математики правила деления
обыкновенных дробей описаны так:
1. Числитель первой дроби умножить на знаменатель
второй дроби.
2. Знаменатель первой дроби умножить на числитель второй дроби.
3. Записать дробь, числитель которой есть результат выполнения пункта 1, а знаменатель — результат выполнения пункта 2. В алгебраической форме это выглядит следующим образом:
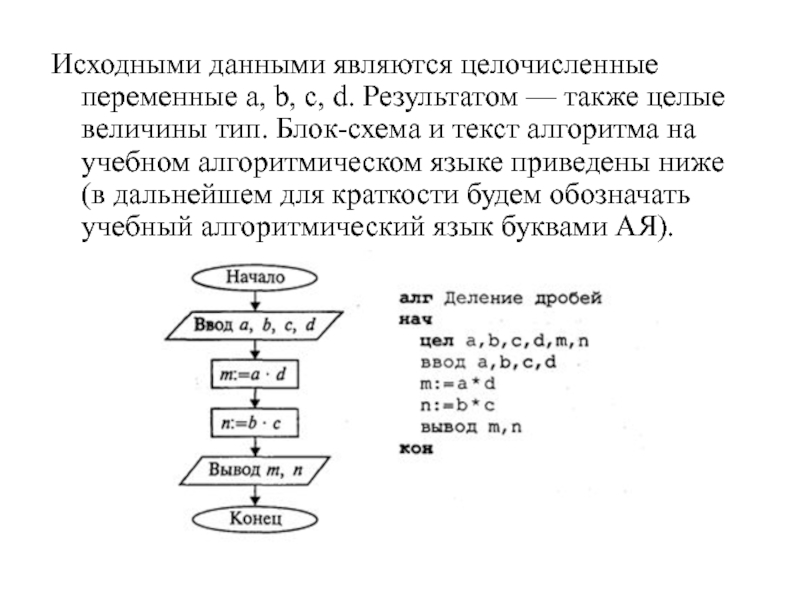
Слайд 18Исходными данными являются целочисленные переменные а, b, с, d. Результатом
— также целые величины тип. Блок-схема и текст алгоритма на
учебном алгоритмическом языке приведены ниже (в дальнейшем для краткости будем обозначать учебный алгоритмический язык буквами АЯ).
Слайд 19Формат команды присваивания следующий:
переменная:=выражение
Знак «:=» нужно читать как «присвоить».
Команда присваивания
обозначает следующие действия, выполняемые компьютером:
1. Вычисляется выражение.
2. Полученное значение присваивается
переменной.
В приведенном выше алгоритме присутствуют две команды присваивания. В блок-схемах команда присваивания записывается в прямоугольнике. Такой блок называется вычислительным блоком.
Слайд 20В приведенном алгоритме присутствует команда ввода:
ввод a,b,c,d
В блок-схеме команда ввода
записывается в параллелограмме — блоке ввода-вывода. При выполнении данной команды
процессор прерывает работу и ожидает действий пользователя. Пользователь должен набрать на устройстве ввода (клавиатуре) значения вводимых переменных и нажать на клавишу ввода Enter. Значения следует вводить в том же порядке, в каком соответствующие переменные расположены в списке ввода
Слайд 21Полученные компьютером результаты решения задачи должны быть сообщены пользователю. Для
этих целей предназначена команда вывода:
вывод m,n
С помощью этой команды результаты
выводятся на экран или на устройство печати на бумагу.
Слайд 22Этот пример иллюстрирует три основных свойства команды присваивания:
• пока переменной
не присвоено значение, она остается неопределенной;
• значение, присвоенное переменной, сохраняется
в ней вплоть до выполнения следующей команды присваивания этой переменной;
• новое значение, присваиваемое переменной, заменяет ее предыдущее значение.