TheSlide.ru

AUTOMAT I C S and AUTOMATIC CONTROL

Содержание

1. AUTOMAT I C S and AUTOMATIC CONTROL
2. Basic dynamic elementsAny, more or less complex
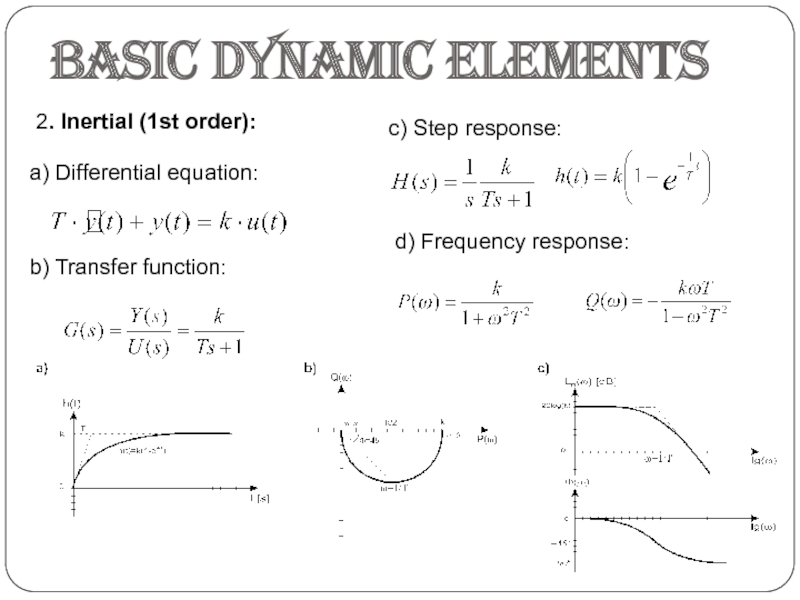
3. Basic dynamic elements2. Inertial (1st order): a) Differential equation:b) Transfer function:c) Step response:d) Frequency response:
4. Basic dynamic elements2. Inertial: e) Example:
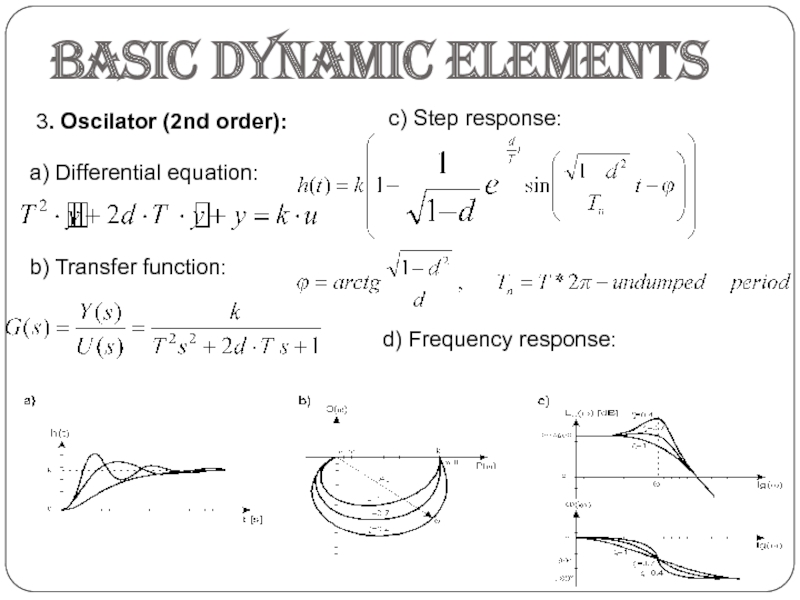
5. Basic dynamic elements3. Oscilator (2nd order): a) Differential equation:b) Transfer function:c) Step response:d) Frequency response:
6. Basic dynamic elements3. Oscilator (2nd order): e) Example1: damped harmonic oscillator
7. Basic dynamic elements3. Oscilator (2nd order): e) Example 2: RLC circuit
8. Basic dynamic elements4. Integrator (ideal integrator): a)
9. Basic dynamic elements5. Real integrator (with inertia): a) Differential equation:b) Transfer function:c) Step response:d) Frequency response:
10. Basic dynamic elements5. Real integrator (with inertia): e) Example: DC motor
11. Basic dynamic elements6. Differentiator (ideal): a) Differential equation:b) Transfer function:c) Step response:d) Frequency response:
12. Basic dynamic elements6. Differentiator (ideal) e) Example: Ideal capasitor
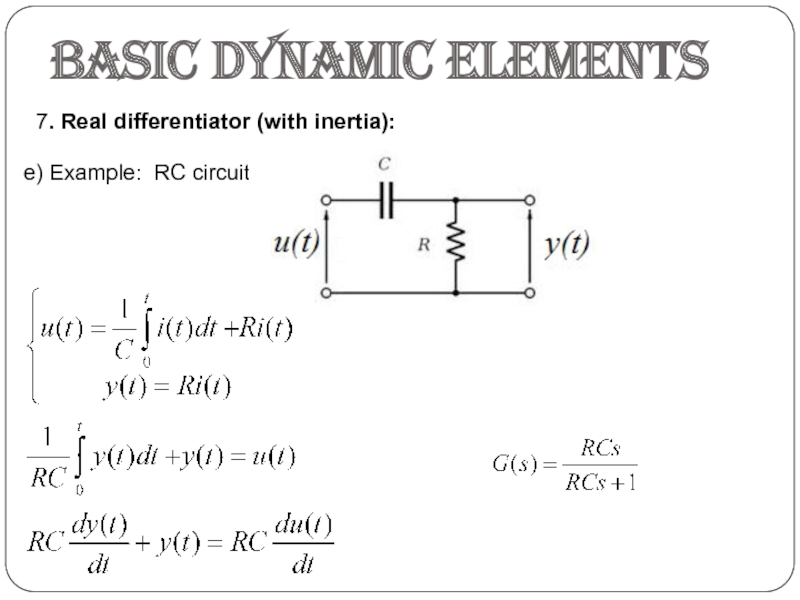
13. Basic dynamic elements7. Real differentiator (with inertia): a) Differential equation:b) Transfer function:c) Step response:d) Frequency response:
14. e) Example: RC circuitBasic dynamic elements7. Real differentiator (with inertia):
15. Basic dynamic elements8. Delaya) Differential equation:b) Transfer function:c) Step response:d) Frequency response:
16. Basic dynamic elements8. Delaye) Example: conveyor (transporter)
17. THANK YOU
18. Слайд 18
19. Скачать презентанцию

Basic dynamic elementsAny, more or less complex systems (objects) can be presented as a connection of some appropriate basic dynamic elements 1. Proportional (noninertial): a) Differential equation:y(t) = k *u(t)b) Transfer

Слайды и текст этой презентации

Слайд 1LECTURE 4

dr inż. Adam Kurnicki
Automation and Metrology Department
Room no 210A

AUTOMATICS

and AUTOMATIC CONTROL

LECTURE 4dr inż. Adam KurnickiAutomation and Metrology DepartmentRoom no 210AAUTOMATICS and AUTOMATIC CONTROL

Слайд 2Basic dynamic elements
Any, more or less complex systems (objects) can

be presented as a connection of some appropriate basic dynamic

elements

1. Proportional (noninertial):

a) Differential equation:

y(t) = k *u(t)

b) Transfer function:

G(s) = k

c) Step response:

H(s) = k/s

h(t) = k1(t)

d) Frequency response:

P(ω) = k

Q(ω) = 0

Lm(ω)=20logk

φ(ω)=0

e) Example:

k=-R2/R1

Basic dynamic elementsAny, more or less complex systems (objects) can be presented as a connection of some

Слайд 3Basic dynamic elements
2. Inertial (1st order):
a) Differential equation:
b) Transfer

function:
c) Step response:
d) Frequency response:

Basic dynamic elements2. Inertial (1st order): a) Differential equation:b) Transfer function:c) Step response:d) Frequency response:

Слайд 4Basic dynamic elements
2. Inertial:
e) Example:

Basic dynamic elements2. Inertial: e) Example:

Слайд 5Basic dynamic elements
3. Oscilator (2nd order):
a) Differential equation:
b) Transfer

function:
c) Step response:
d) Frequency response:

Basic dynamic elements3. Oscilator (2nd order): a) Differential equation:b) Transfer function:c) Step response:d) Frequency response:

Слайд 6Basic dynamic elements
3. Oscilator (2nd order):
e) Example1: damped harmonic

oscillator

Basic dynamic elements3. Oscilator (2nd order): e) Example1: damped harmonic oscillator

Слайд 7Basic dynamic elements
3. Oscilator (2nd order):
e) Example 2: RLC

circuit

Basic dynamic elements3. Oscilator (2nd order): e) Example 2: RLC circuit

Слайд 8Basic dynamic elements
4. Integrator (ideal integrator):
a) Differential equation:
b) Transfer

function:
c) Step response:
d) Frequency response:
Lm(ω)=-20logωTi
φ(ω)=-π/2
e) Example: (water flow q to

the tank with water level area Ch ):

Basic dynamic elements4. Integrator (ideal integrator): a) Differential equation:b) Transfer function:c) Step response:d) Frequency response:Lm(ω)=-20logωTiφ(ω)=-π/2e) Example: (water

Слайд 9Basic dynamic elements
5. Real integrator (with inertia):
a) Differential equation:
b)

Transfer function:
c) Step response:
d) Frequency response:

Basic dynamic elements5. Real integrator (with inertia): a) Differential equation:b) Transfer function:c) Step response:d) Frequency response:

Слайд 10Basic dynamic elements
5. Real integrator (with inertia):
e) Example: DC

motor

Basic dynamic elements5. Real integrator (with inertia): e) Example: DC motor

Слайд 11
Basic dynamic elements
6. Differentiator (ideal):
a) Differential equation:
b) Transfer

function:
c) Step response:
d) Frequency response:

Basic dynamic elements6. Differentiator (ideal): a) Differential equation:b) Transfer function:c) Step response:d) Frequency response:

Слайд 12Basic dynamic elements
6. Differentiator (ideal)
e) Example: Ideal capasitor

Basic dynamic elements6. Differentiator (ideal) e) Example: Ideal capasitor

Слайд 13Basic dynamic elements
7. Real differentiator (with inertia):
a) Differential equation:
b)

Transfer function:
c) Step response:
d) Frequency response:

Basic dynamic elements7. Real differentiator (with inertia): a) Differential equation:b) Transfer function:c) Step response:d) Frequency response:

Слайд 14e) Example: RC circuit
Basic dynamic elements
7. Real differentiator (with inertia):

e) Example: RC circuitBasic dynamic elements7. Real differentiator (with inertia):

Слайд 15Basic dynamic elements
8. Delay
a) Differential equation:
b) Transfer function:
c) Step response:
d)

Frequency response:

Basic dynamic elements8. Delaya) Differential equation:b) Transfer function:c) Step response:d) Frequency response:

Слайд 16Basic dynamic elements
8. Delay
e) Example: conveyor (transporter)

Basic dynamic elements8. Delaye) Example: conveyor (transporter)

Слайд 17THANK YOU

THANK YOU

Слайд 18

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей