Слайд 1ЭКЗАМЕНАЦИОННЫЕ БИЛЕТЫ ПО ЧЕРЧЕНИЮ
9 КЛАСС
Слайд 2Билет-№1
1.Аксонометрические проекции. Прямоугольная изометрическая проекция детали.
2.Приемы деления окружности на 3,
6, 12 частей с помощью циркуля.
Аксонометрические проекции представляют собой наглядное
и достаточно точное изображение предметов. Слово «аксонометрия» — греческое. Оно состоит из двух слов: ахсоп — ось и metreo — измерение, что означает измерение по осям (или измерение параллельно осям).
Стандарт устанавливает несколько типов аксонометрических проекций. Познакомимся с двумя из них: косоугольной фронтальной диметрической проекцией (в ГОСТ 2.317-69 ее кратко называют фронтальной диметрической проекцией) и прямоугольной изометрической проекцией (сокращенный вариант названия — изометрическая проекция).
Получение косоугольной фронтальной диметрической проекции
Координатные оси z и х расположены относительно друг друга под углом 90°. Ось х (продолжение оси) по отношению к оси у расположилась под углом 45°
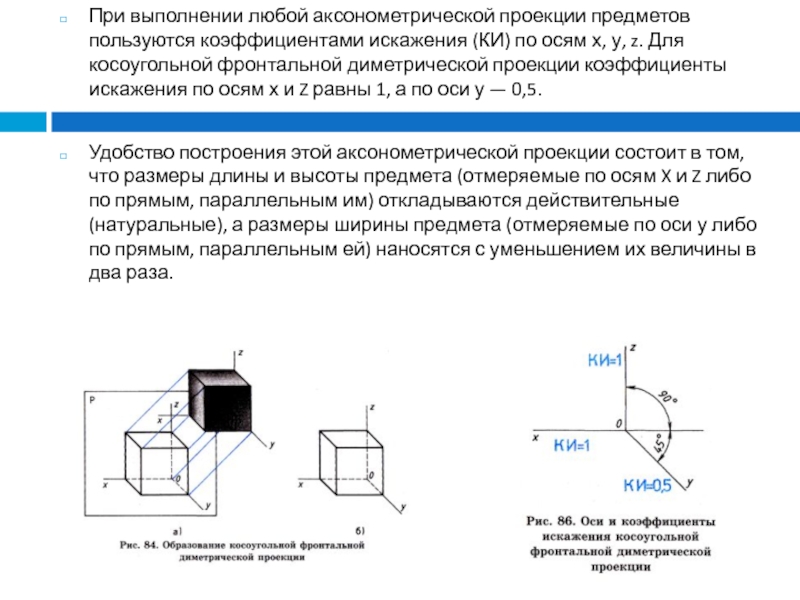
Слайд 3При выполнении любой аксонометрической проекции предметов пользуются коэффициентами искажения (КИ)
по осям х, у, z. Для косоугольной фронтальной диметрической проекции
коэффициенты искажения по осям х и Z равны 1, а по оси у — 0,5.
Удобство построения этой аксонометрической проекции состоит в том, что размеры длины и высоты предмета (отмеряемые по осям X и Z либо по прямым, параллельным им) откладываются действительные (натуральные), а размеры ширины предмета (отмеряемые по оси у либо по прямым, параллельным ей) наносятся с уменьшением их величины в два раза.
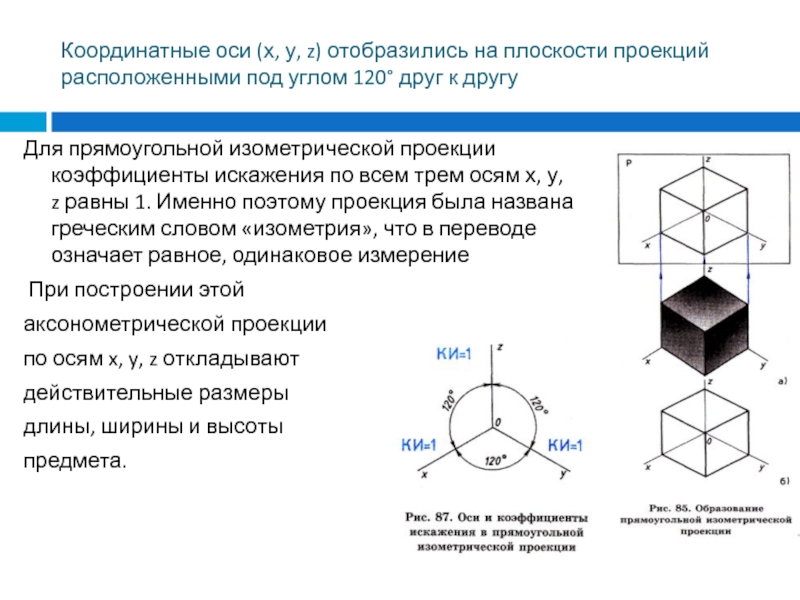
Слайд 4Координатные оси (х, у, z) отобразились на плоскости проекций расположенными
под углом 120° друг к другу
Для прямоугольной изометрической проекции коэффициенты
искажения по всем трем осям х, у, z равны 1. Именно поэтому проекция была названа греческим словом «изометрия», что в переводе означает равное, одинаковое измерение
При построении этой
аксонометрической проекции
по осям x, y, z откладывают
действительные размеры
длины, ширины и высоты
предмета.
Слайд 52. Деление окружности на три, шесть, двенадцать равных частей. Построение
правильных многоугольников.
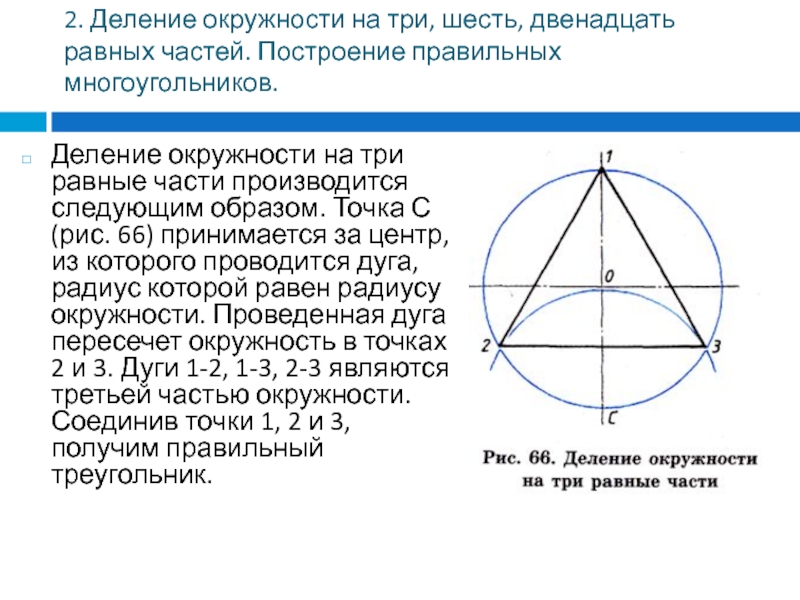
Деление окружности на три равные части производится следующим образом.
Точка С (рис. 66) принимается за центр, из которого проводится дуга, радиус которой равен радиусу окружности. Проведенная дуга пересечет окружность в точках 2 и 3. Дуги 1-2, 1-3, 2-3 являются третьей частью окружности. Соединив точки 1, 2 и 3, получим правильный треугольник.
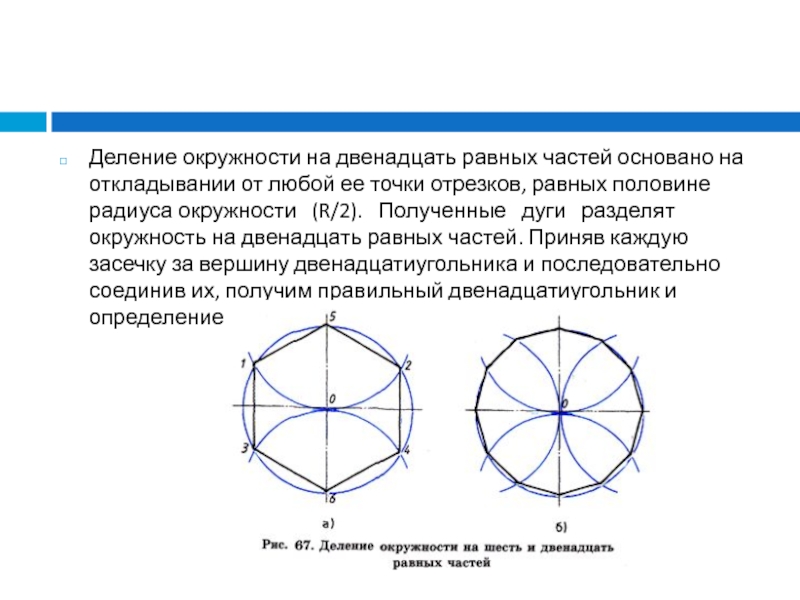
Слайд 6Деление окружности на двенадцать равных частей основано на откладывании от
любой ее точки отрезков, равных половине радиуса окружности (R/2).
Полученные дуги разделят окружность на двенадцать равных частей. Приняв каждую засечку за вершину двенадцатиугольника и последовательно соединив их, получим правильный двенадцатиугольник и определение величины радиуса (рис. 67, б)
Слайд 7Билет -2
1. Разрезы (вырезы) в аксонометрических проекциях.
2. Приёмы деления окружности
на 4, 8,16 частей с помощью циркуля.
На аксонометрических проекциях для
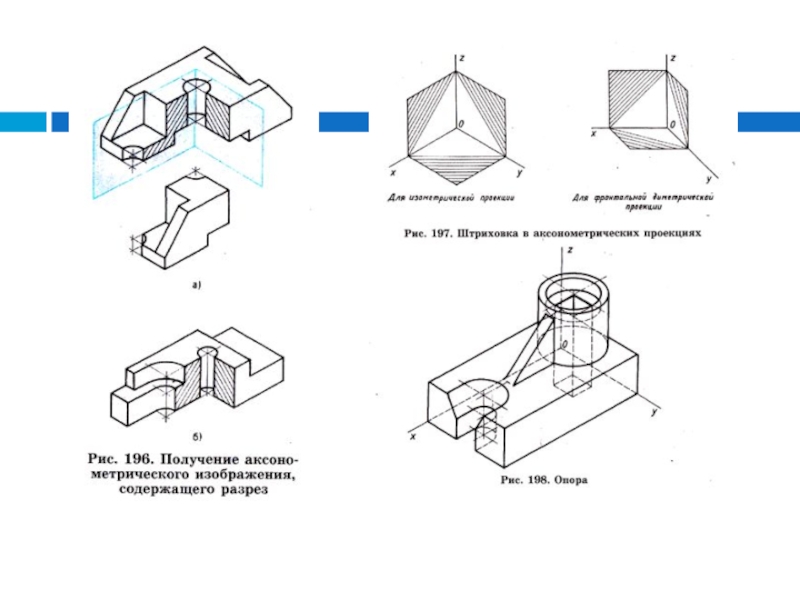
выявления внутренней формы также применяют разрезы. Получение аксонометрического изображения, содержащего разрез, показано на рис. 196.
Секущие плоскости выбираются таким образом, чтобы они совпадали с плоскостями симметрии (рис. 196, а) либо проходили через оси отверстий, пазов, углублений (рис. 196, б).
Штриховка на аксонометрических изображениях сечений наносится так, как показано на рис. 197, т. е. параллельно диагоналям проекций квадратов, построенных на осях X и Z, X и Y, Y и Z.
Слайд 92 Деление окружности на четыре, восемь равных частей.
Построение правильного
четырехугольника и восьмиугольника.
Штрихпунктирные центровые линии, проведенные перпендикулярно одна другой, делят
окружность на четыре равные части. Последовательно соединив их концы, получим правильный четырехугольник (рис. 64).
Для того чтобы разделить окружность на восемь равных частей, необходимо разделить на две равные части дугу, равную 1/4 окружности. Таким образом получим дугу, равную 1/8 окружности (А4 = A3). Раствором циркуля, равным A3 или А4, нанесем засечки на окружности, разделив ее тем самым на восемь равных частей. Последовательно соединив засечки отрезками прямых, получим правильный восьмиугольник
Слайд 10Билет 3
1 Проецирование. Центральное и параллельное проецирование.
2 Приемы деления прямой
на n-равное количество отрезков.
1 Проецирование — процесс получения проекции
предмета (изображения предмета на плоскости).
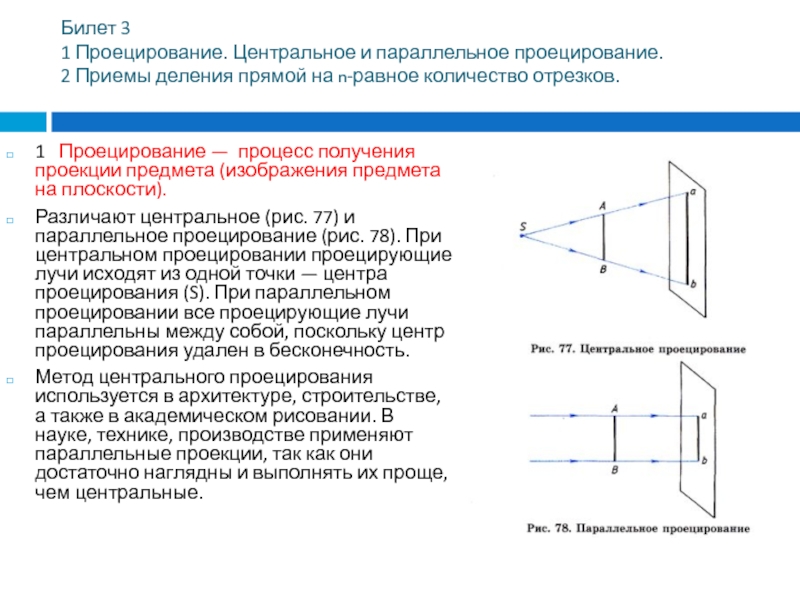
Различают центральное (рис. 77) и параллельное проецирование (рис. 78). При центральном проецировании проецирующие лучи исходят из одной точки — центра проецирования (S). При параллельном проецировании все проецирующие лучи параллельны между собой, поскольку центр проецирования удален в бесконечность.
Метод центрального проецирования используется в архитектуре, строительстве, а также в академическом рисовании. В науке, технике, производстве применяют параллельные проекции, так как они достаточно наглядны и выполнять их проще, чем центральные.
Слайд 11Параллельное проецирование подразделяется на прямоугольное (рис. 79) и косоугольное (рис.
80).
При прямоугольном (ортогональном) проецировании проецирующие лучи падают на плоскость
под прямым углом (рис. 79). При косоугольном проецировании проецирующие лучи падают на плоскость под углом, отличным от прямого (рис. 80).
Слайд 12Допустим, отрезок АВ необходимо разделить на пять равных частей
Из любого
конца заданного отрезка АВ проводим луч. С помощью циркуля от
точки А на луче откладывается необходимое количество (пять в нашем случае) равных отрезков.
Соединяем точки 5 и В прямой линией. Прикладываем к линии 5В рабочую сторону угольника и подводим к нему линейку. Передвигаем угольник параллельно полученной прямой и через точки 4, 3, 2, 1 проводим линии до пересечения с отрезком АВ, которые разделят его на заданное число равных частей
Слайд 13Билет 4
1.Прямоугольное проецирование на три взаимно перпендикулярные плоскости проекций.
2.Приёмы деления
окружностей на 5 равных частей с помощью циркуля.
Чтобы получить
точное и полное представление о форме, предмет проецируют на две плоскости проекций V и Н или V и W
Необходимость в третьей проекции возникает тогда, когда и двух проекций бывает недостаточно для определения формы предмета.
Для получения точного и полного представления о форме предмета используют проецирование на три плоскости проекций V, Н и W
В данном случае профильная проекция детали дает возможность точно определить форму каждой из них.
На чертежах допускается не показывать оси проекций, линии проекционной связи и постоянную прямую чертежа.
Слайд 142. Деление окружности на пять и десять равных частей. Построение
правильных пятиугольника и десятиугольника.
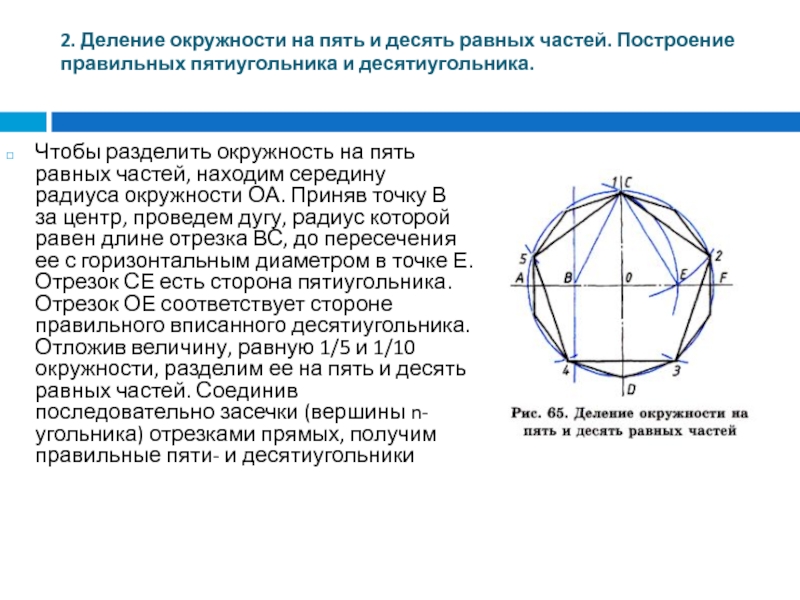
Чтобы разделить окружность на пять равных частей,
находим середину радиуса окружности ОА. Приняв точку В за центр, проведем дугу, радиус которой равен длине отрезка ВС, до пересечения ее с горизонтальным диаметром в точке Е. Отрезок СЕ есть сторона пятиугольника. Отрезок ОЕ соответствует стороне правильного вписанного десятиугольника. Отложив величину, равную 1/5 и 1/10 окружности, разделим ее на пять и десять равных частей. Соединив последовательно засечки (вершины n-угольника) отрезками прямых, получим правильные пяти- и десятиугольники
Слайд 15
Билет 5
1.Прямоугольные проекции. Использование их в практической деятельности.
2.Сопряжение прямого. Тупого
и острого углов.
Если проецирующие лучи параллельны между собой и падают
на плоскость проекций под прямым углом, то проецирование называется прямоугольным, а полученные проекции прямоугольными.
В промышленности широко используются плоские детали(пластины.уголки, прокладки. Решетки. Лекала швейного и обувного производства). Для отображения их на чертеже достаточно построения одной проекции.
Слайд 16Плавный переход одной линии в другую называется сопряжением.
Общая для
сопрягаемых линий точка называется точкой сопряжения, или точкой перехода. Для
построения сопряжений надо найти центр сопряжения и точки сопряжений.
Сопряжение прямого угла. Пусть необходимо выполнить сопряжение прямого угла радиусом сопряжения, равным отрезку АВ (R=AB). Найдем точки сопряжения. Для этого поставим ножку циркуля в вершину угла и раствором циркуля, равным отрезку АВ, сделаем засечки на сторонах угла. Полученные точки а и b являются точками сопряжения. Найдем центр сопряжения — точку, равноудаленную от сторон угла. Раствором циркуля, равным радиусу сопряжения, из точек а и b проведем внутри угла две дуги до пересечения друг с другом. Полученная точка О — центр сопряжения. Из центра сопряжения описываем дугу заданного радиуса от точки а до точки Ь. Обводим вначале дугу, а затем прямые линии
Слайд 17Сопряжение острого и тупого углов.
Чтобы построить сопряжение острого угла,
возьмем раствор циркуля, равный заданному радиусу R=AB. Поочередно поставим ножку
циркуля в две произвольные точки на каждой из сторон острого угла. Проведем четыре дуги внутри угла, как показано на р. 71, а. К ним проведем две касательные до пересечения в точке О — центре сопряжения (рис. 71, б)- Из центра сопряжения опустим перпендикуляры на стороны угла. Полученные точки а и b будут точками сопряжения (рис. 71, б). Поставив ножку циркуля в центр сопряжения (О), раствором циркуля, равным заданному радиусу сопряжения (R=AB), проведем дугу сопряжения.
Аналогично построению сопряжения острого угла строят сопряжение (скругление) тупого угла.
Слайд 18Билет 6
1Технический рисунок: получение, оттенение. Использование в практической деятельности.
2 Сопряжение
окружности с прямой дугой заданного радиуса.
Технический рисунок — наглядное изображение
предмета, выполненное по правилам аксонометрических проекций без чертежных инструментов (от руки), в глазомерном масштабе, с соблюдением пропорциональных соотношений размеров.
Форма предмета на техническом рисунке выявляется с помощью оттенения. Оно осуществляется приемами шатировки (штрихами), шраффировки (штриховка в виде сетки) и точечным оттенением (рис. 99).
При выполнении оттенения принято считать, что свет падает на предмет слева сверху. Освещенные поверхности не заштриховываются, а затененные покрывают штриховкой. Чем темнее часть поверхности, тем более частой должна быть штриховка.
Технические рисунки давно используются людьми для раскрытия творческого замысла.
Инженеры. Дизайнеры. Архитекторы при проектировании новых образцов техники, изделий, сооружений используют технический рисунок как средство фиксации первых, промежуточных и окончательных вариантов решения технического замысла. Служат для проверки правильности прочтения сложной формы, отображенной на чертеже.

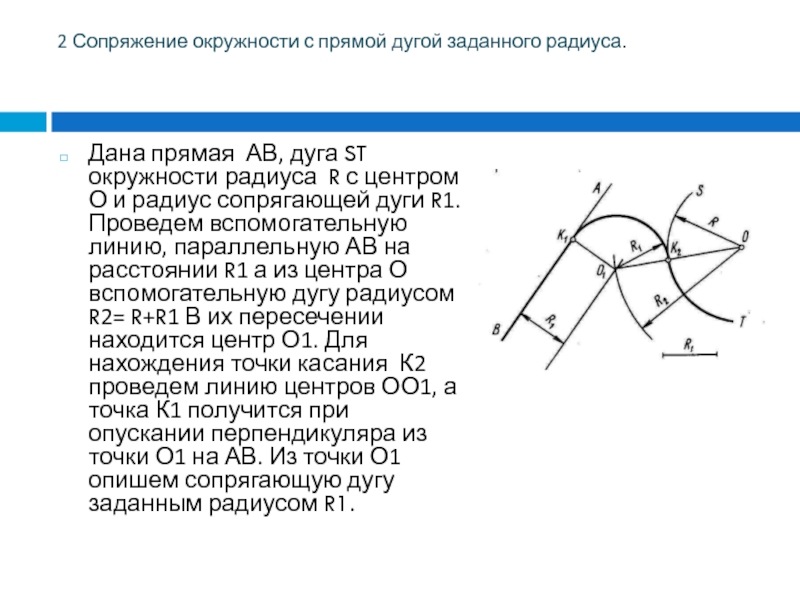
Слайд 19Дана прямая АВ, дуга ST окружности радиуса R с центром
О и радиус сопрягающей дуги R1. Проведем вспомогательную линию, параллельную
АВ на расстоянии R1 а из центра О вспомогательную дугу радиусом R2= R+R1 В их пересечении находится центр О1. Для нахождения точки касания К2 проведем линию центров ОО1, а точка К1 получится при опускании перпендикуляра из точки О1 на АВ. Из точки О1 опишем сопрягающую дугу заданным радиусом R1.
2 Сопряжение окружности с прямой дугой заданного радиуса.
Слайд 20 Билет 7
1.Разрезы: назначение, получение, классификация.
2 Сопряжение двух параллельных
прямых.
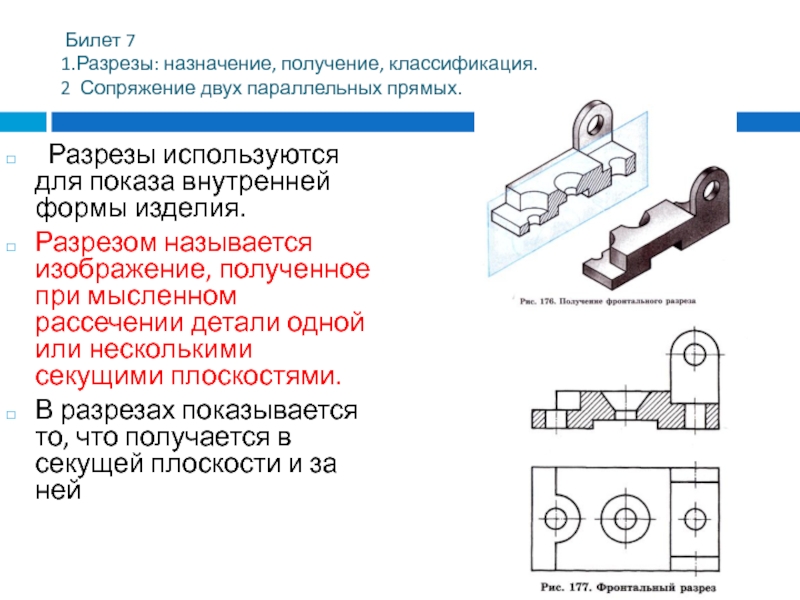
Разрезы используются для показа внутренней формы изделия.
Разрезом называется изображение,
полученное при мысленном рассечении детали одной или несколькими секущими плоскостями.
В разрезах показывается то, что получается в секущей плоскости и за ней
Слайд 21То, что находится за секущей плоскостью, считается видимым и поэтому
изображается сплошной толстой основной линией (рис. 177).
На чертежах используются простые
и сложные разрезы. Простыми разрезами называются такие разрезы, которые получены при мысленном рассечении детали одной секущей плоскостью. Сложными разрезами называются разрезы, полученные при мысленном рассечении детали двумя и большим количеством плоскостей (они не изучаются по школьной программе).
Познакомимся с простыми разрезами: фронтальным, горизонтальным, профильным.
Фронтальный разрез получается при мысленном рассечении детали секущей плоскостью, параллельной фронтальной плоскости проекции (рис. 176).
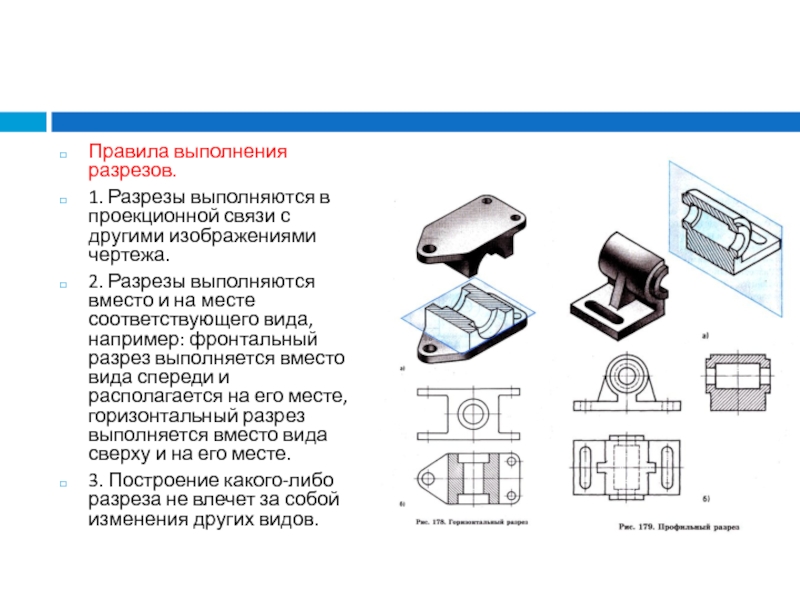
Горизонтальный разрез получается при мысленном рассечении детали секущей плоскостью, параллельной горизонтальной плоскости проекций (рис. 178).
Профильный разрез получаем при мысленном рассечении детали секущей плоскостью, параллельной профильной плоскости проекций (рис. 179).
Слайд 22Правила выполнения разрезов.
1. Разрезы выполняются в проекционной связи с другими
изображениями чертежа.
2. Разрезы выполняются вместо и на месте соответствующего вида,
например: фронтальный разрез выполняется вместо вида спереди и располагается на его месте, горизонтальный разрез выполняется вместо вида сверху и на его месте.
3. Построение какого-либо разреза не влечет за собой изменения других видов.
Слайд 232 Сопряжение двух параллельных прямых.
Заданы две параллельные прямые и точка
d, лежащая на одной из них (рис.72). Рассмотрим последовательность построения
сопряжения двух прямых. В точке d восставим перпендикуляр до пересечения его с другой прямой. Точки d и е являются точками сопряжения. Разделив отрезок de пополам, найдем центр сопряжения. Из него радиусом сопряжения проводим дугу, сопрягающую прямые.
Слайд 24Билет 8
1 Простые разрезы
2 Сопряжение двух окружностей дугой заданного
радиуса
(внутреннее сопряжение)
Разрезом называется изображение, полученное при мысленном рассечении детали одной
или несколькими секущими плоскостями.
В разрезах показывается то, что получается в секущей плоскости и за ней.
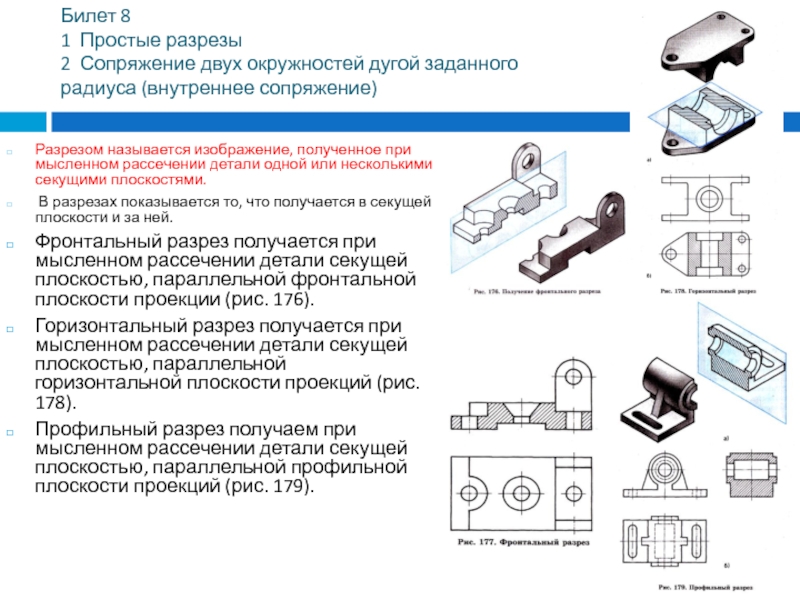
Фронтальный разрез получается при мысленном рассечении детали секущей плоскостью, параллельной фронтальной плоскости проекции (рис. 176).
Горизонтальный разрез получается при мысленном рассечении детали секущей плоскостью, параллельной горизонтальной плоскости проекций (рис. 178).
Профильный разрез получаем при мысленном рассечении детали секущей плоскостью, параллельной профильной плоскости проекций (рис. 179).
Слайд 25Сопряжение двух окружностей дугой заданного радиуса (внутреннее сопряжение)
Существует несколько типов
сопряжения дуг двух окружностей дугой заданного радиуса: внешнее, внутреннее и
смешанное.
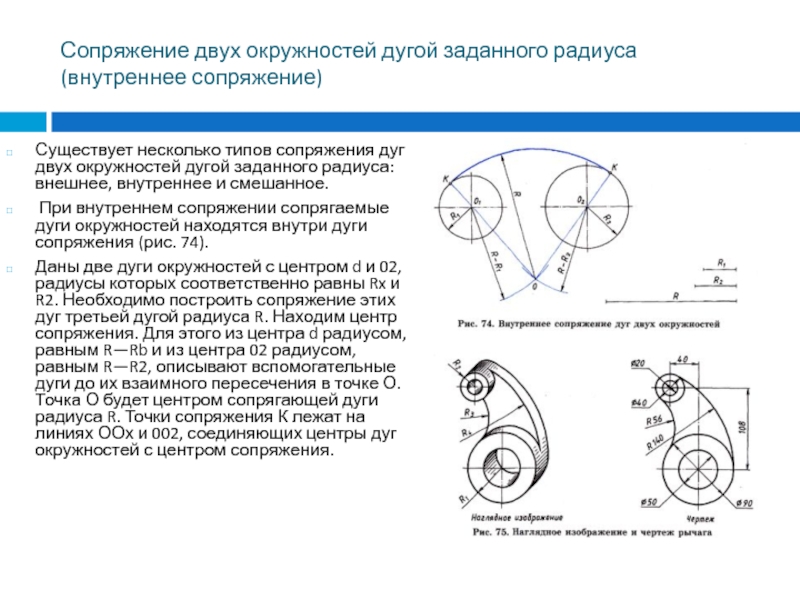
При внутреннем сопряжении сопрягаемые дуги окружностей находятся внутри дуги сопряжения (рис. 74).
Даны две дуги окружностей с центром d и 02, радиусы которых соответственно равны Rx и R2. Необходимо построить сопряжение этих дуг третьей дугой радиуса R. Находим центр сопряжения. Для этого из центра d радиусом, равным R—Rb и из центра 02 радиусом, равным R—R2, описывают вспомогательные дуги до их взаимного пересечения в точке О. Точка О будет центром сопрягающей дуги радиуса R. Точки сопряжения К лежат на линиях ООх и 002, соединяющих центры дуг окружностей с центром сопряжения.
Слайд 26Билет 9
1 Изображение и обозначение разрезов на чертеже.
2Сопряжение двух окружностей
дугой заданного радиуса (внешнее сопряжение)
Правила выполнения разрезов.
1. Разрезы выполняются в
проекционной связи с другими изображениями чертежа.
2. Разрезы выполняются вместо и на месте соответствующего вида, например: фронтальный разрез выполняется вместо вида спереди и располагается на его месте, горизонтальный разрез выполняется вместо вида сверху и на его месте.
3. Построение какого-либо разреза не влечет за собой изменения других видов.
Правила обозначения разрезов.
Разрезы на чертеже, как правило, обозначаются. Однако есть случаи, когда обозначение разреза не наносится. Рассмотрим правила обозначения разрезов:
1. Если секущая плоскость совпадает с плоскостью симметрии детали, то разрез на чертеже не обозначается
2. Если секущая плоскость не совпадает с плоскостью симметрии детали, то разрез обозначается следующим образом. Положение секущей плоскости показывают штрихами разомкнутой линии. К штрихам разомкнутой линии на расстоянии 2-3 мм от внешнего края ставят стрелки, указывающие направление взгляда (рис. 180). С внешней стороны стрелок пишут прописные буквы русского алфавита. Изображение разреза подписывается надписью типа А-А, Б-Б

Слайд 272Сопряжение двух окружностей дугой заданного радиуса (внешнее сопряжение)
Существует несколько типов
сопряжения дуг двух окружностей дугой заданного радиуса: внешнее, внутреннее и
смешанное.
Рассмотрим пример внешнего сопряжения дуг двух окружностей дугой заданного радиуса. Заданы радиусы Rx и R2 дуг двух окружностей (длины радиусов показаны отрезками прямых). Необходимо построить их сопряжение третьей дугой радиуса R (рис. 73, а). Для нахождения центра сопряжения проводим две вспомогательные дуги: одну радиусом ОхО = Ri + R, а другую 020 = R2 + R. Точка пересечения вспомогательных дуг является центром сопряжения. Точки сопряжения К лежат в пересечении прямых dO и 020 с дугами заданных окружностей. Из центра сопряжения радиусом сопряжения проводим дугу, соединяя точки сопряжений. При обводке построений вначале изображают дугу сопряжения, а затем дуги сопрягаемых окружностей
Слайд 28Билет 10
1 Сечения:назначение, получение, классификация.
2 Деление прямого угла на две
и три равные части с помощью циркуля.
1 Сечением
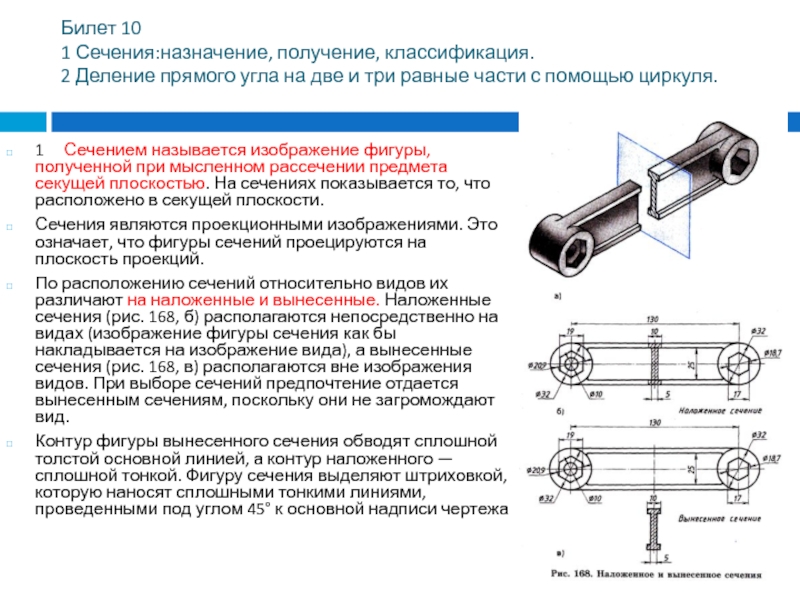
называется изображение фигуры, полученной при мысленном рассечении предмета секущей плоскостью. На сечениях показывается то, что расположено в секущей плоскости.
Сечения являются проекционными изображениями. Это означает, что фигуры сечений проецируются на плоскость проекций.
По расположению сечений относительно видов их различают на наложенные и вынесенные. Наложенные сечения (рис. 168, б) располагаются непосредственно на видах (изображение фигуры сечения как бы накладывается на изображение вида), а вынесенные сечения (рис. 168, в) располагаются вне изображения видов. При выборе сечений предпочтение отдается вынесенным сечениям, поскольку они не загромождают вид.
Контур фигуры вынесенного сечения обводят сплошной толстой основной линией, а контур наложенного — сплошной тонкой. Фигуру сечения выделяют штриховкой, которую наносят сплошными тонкими линиями, проведенными под углом 45° к основной надписи чертежа
Слайд 29Построение углов при помощи угольников
При помощи линейки и угольников с
углами 30°, 60°, 90° и 45°, 45°, 90° можно построить
любой угол, кратный 15°, в зависимости от того, в какой комбинации будем сочетать их углы. Внимательно рассмотрите положение угольников при построении различных углов (рис. 62) и используйте эти знания при выполнении чертежей.
Деление углов на равные части. Чтобы разделить прямой угол (например угол ABC) на три равные части, из вершины угла (точки В) проводим дугу произвольного радиуса R до пересечения со сторонами угла в точках D и Е. Из точек D и Е, как из центров, радиусом R = BE или BD, проводим дуги, пересекающие дугу DE в точках F и Н, получим углы ABF = FBH = НВЕ = 30° (рис. 63). Деление угла на две равные части и построение угла, равного данному, вы изучали на уроках геометрии. Вспомните этот материал самостоятельно, вам он понадобится на уроках черчения
С помощью транспортира можно построить любой угол и разделить его на равные части
Слайд 30Билет 11
1. Вынесенные сечения. Обозначение вынесенных сечений.
2 Построение перпендикуляра к
отрезку прямой через точку, лежащую вне прямой.
вынесенные сечения располагаются вне
изображения видов. При выборе сечений предпочтение отдается вынесенным сечениям, поскольку они не загромождают вид.
Вначале изучаем форму детали, находим конструктивные элементы, которые должны быть выявлены с помощью сечений.
Мысленно рассекаем деталь секущей (секущими) плоскостью (плоскостями) и представляем полученную фигуру сечения.
Выбираем место для построения сечения (сечений), наносим оси симметрии для симметричных изображений. Вычерчиваем фигуру сечения.
При построении изображения фигуры (фигур) сечения размеры следует снимать с других изображений чертежа — видов, разрезов. Контур фигуры вынесенного сечения обводят сплошной толстой основной линией, а контур наложенного — сплошной тонкой. Фигуру сечения выделяют штриховкой, которую наносят сплошными тонкими линиями, проведенными под углом 45° к основной надписи чертежа (рис. 168, б, в)
Правила обозначения вынесенных сечений. Вынесенные сечения могут располагаться в разрыве между частями одного и того же вида (рис. 169 а, б), на свободном месте (рис. 169, в), на продолжении штрихпунктирной линии (рис. 169, г).

Слайд 31Построение перпендикуляра к отрезку прямой через точку, лежащую вне прямой.
Перпендикуляр
к прямой АВ из заданной точки С строят следующим образом
радиусом произвольного размера R1 из точки С проводят дугу и отмечают точки D и E пересечения её с прямой АВ
тем же или другим радиусом R2 ставя попеременно иглу циркуля в точки D и E делают засечки для определения точки F , получают искомый перпендикуляр.
Слайд 32Билет 12
1 Фронтальный разрез.
2 Построение перпендикуляра к отрезку через точку
, лежащую на ней.
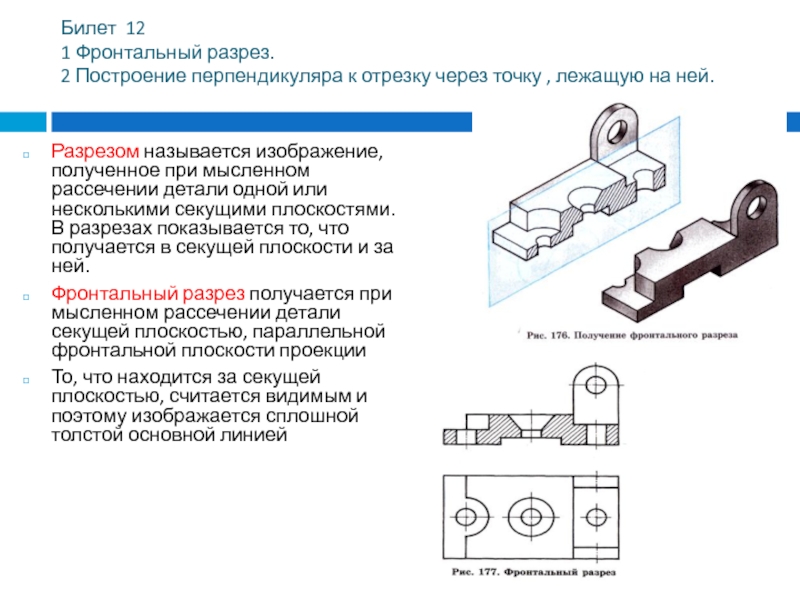
Разрезом называется изображение, полученное при мысленном рассечении
детали одной или несколькими секущими плоскостями. В разрезах показывается то, что получается в секущей плоскости и за ней.
Фронтальный разрез получается при мысленном рассечении детали секущей плоскостью, параллельной фронтальной плоскости проекции
То, что находится за секущей плоскостью, считается видимым и поэтому изображается сплошной толстой основной линией
Слайд 33Построение перпендикуляра к отрезку через точку , лежащую на ней.
2
Чтобы построить перпендикуляр к прямой через заданную-точку с помощью рейсшины,
необходимо переместить ее ниже заданной прямой. К рейсшине приложить угольник так, как показано на рис. 59, совместив положение стороны угольника с заданной точкой. Затем провести прямую, которая будет перпендикулярна заданной. Этот же случай рассмотрен на примере построения перпендикуляра с использованием двух угольников
Слайд 34Билет 13
1 Горизонтальный разрез
2 Построение различных углов с помощью угольников.
1
Разрезом называется изображение, полученное при мысленном рассечении детали одной
или несколькими секущими плоскостями. В разрезах показывается то, что получается в секущей плоскости и за ней.
Горизонтальный разрез получается при мысленном рассечении детали секущей плоскостью, параллельной горизонтальной плоскости проекций
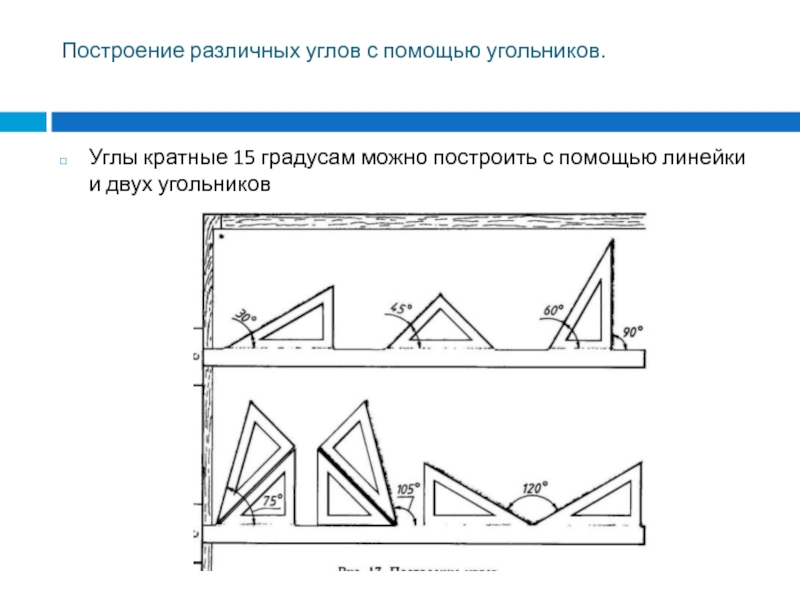
Слайд 35Построение различных углов с помощью угольников.
Углы кратные 15 градусам можно
построить с помощью линейки и двух угольников
Слайд 36Билет 14
1 Профильный разрез
2 Условные знаки, используемые для передачи информации
о форме изделия.
Разрезом называется изображение, полученное при мысленном рассечении детали
одной или несколькими секущими плоскостями. В разрезах показывается то, что получается в секущей плоскости и за ней.
Профильный разрез получаем при мысленном рассечении детали секущей плоскостью, параллельной профильной плоскости проекций
2
Слайд 37Билет 15
1 Изображение и обозначение резьбы на чертежах.
2 Типы линий
чертежах как основные элементы графического языка.
С помощью резьбы производится свинчивание
деталей либо их соединение с использованием специальных крепежных изделий (болт, винт, шпилька, гайка и т. д.). Соединение, осуществляемое с помощью резьбы, относится к резьбовым соединениям
Резьба — это поверхность, образованная при винтовом движении плоского контура по цилиндрической (конической) поверхности.
Различают резьбы крепежные (для соединения деталей), крепежно-уплотнительные (для плотных соединений труб с помощью специальных деталей — муфт) и ходовые (для преобразования вращательного движения в поступательное и наоборот).
Резьба характеризуется различными параметрами, познакомимся с некоторыми из них.
Наружный диаметр резьбы (d) — диаметр, измеряемый по выступам профиля резьбы на стержне или по впадинам в отверстии (рис. 206, а).
Внутренний диаметр резьбы (d1) — диаметр, измеренный по впадинам профиля резьбы на стержне или по выступам в отверстии (рис. 206, а).
Профиль резьбы — фигура сечения резьбы, получаемая в плоскости, проходящей через ось (рис. 206, б).
Шаг резьбы (р) — расстояние между соседними одноименными боковыми сторонами двух соседних витков резьбы

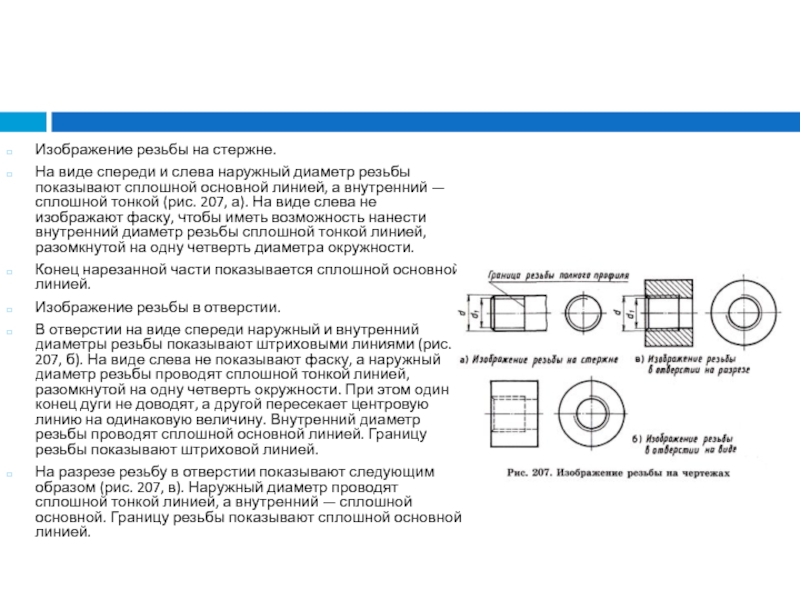
Слайд 38Изображение резьбы на стержне.
На виде спереди и слева наружный диаметр
резьбы показывают сплошной основной линией, а внутренний — сплошной тонкой
(рис. 207, а). На виде слева не изображают фаску, чтобы иметь возможность нанести внутренний диаметр резьбы сплошной тонкой линией, разомкнутой на одну четверть диаметра окружности.
Конец нарезанной части показывается сплошной основной линией.
Изображение резьбы в отверстии.
В отверстии на виде спереди наружный и внутренний диаметры резьбы показывают штриховыми линиями (рис. 207, б). На виде слева не показывают фаску, а наружный диаметр резьбы проводят сплошной тонкой линией, разомкнутой на одну четверть окружности. При этом один конец дуги не доводят, а другой пересекает центровую линию на одинаковую величину. Внутренний диаметр резьбы проводят сплошной основной линией. Границу резьбы показывают штриховой линией.
На разрезе резьбу в отверстии показывают следующим образом (рис. 207, в). Наружный диаметр проводят сплошной тонкой линией, а внутренний — сплошной основной. Границу резьбы показывают сплошной основной линией.
Слайд 39Типы линий чертежах как основные элементы графического языка.
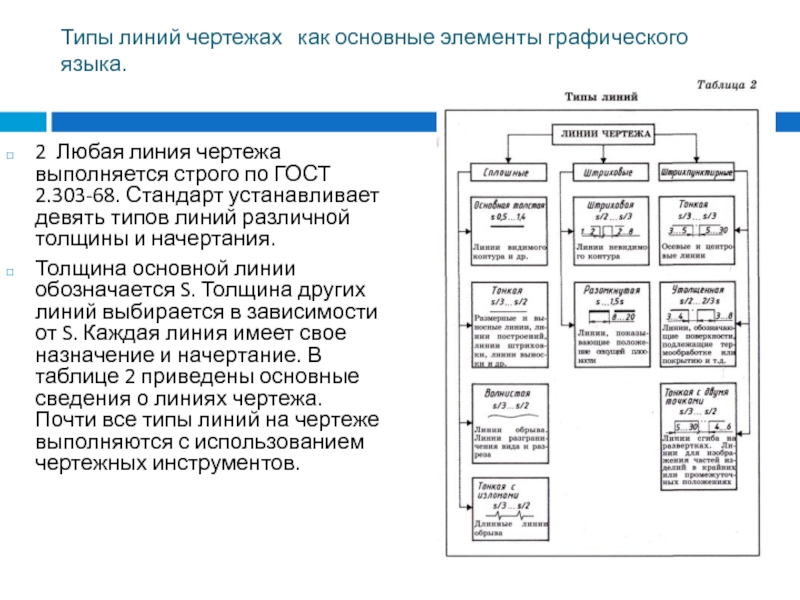
2 Любая
линия чертежа выполняется строго по ГОСТ 2.303-68. Стандарт устанавливает девять
типов линий различной толщины и начертания.
Толщина основной линии обозначается S. Толщина других линий выбирается в зависимости от S. Каждая линия имеет свое назначение и начертание. В таблице 2 приведены основные сведения о линиях чертежа. Почти все типы линий на чертеже выполняются с использованием чертежных инструментов.
Слайд 40Билет 16
1. Виды(основные, местные)
2 .Приемы начертания параллельных, вертикальных и горизонтальных
отрезков прямых
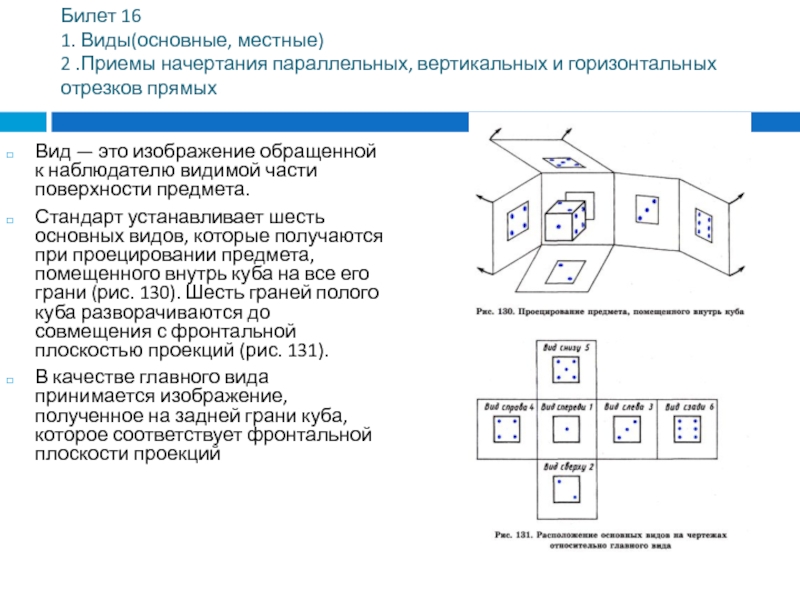
Вид — это изображение обращенной к наблюдателю видимой части
поверхности предмета.
Стандарт устанавливает шесть основных видов, которые получаются при проецировании предмета, помещенного внутрь куба на все его грани (рис. 130). Шесть граней полого куба разворачиваются до совмещения с фронтальной плоскостью проекций (рис. 131).
В качестве главного вида принимается изображение, полученное на задней грани куба, которое соответствует фронтальной плоскости проекций
Слайд 41Местный вид.
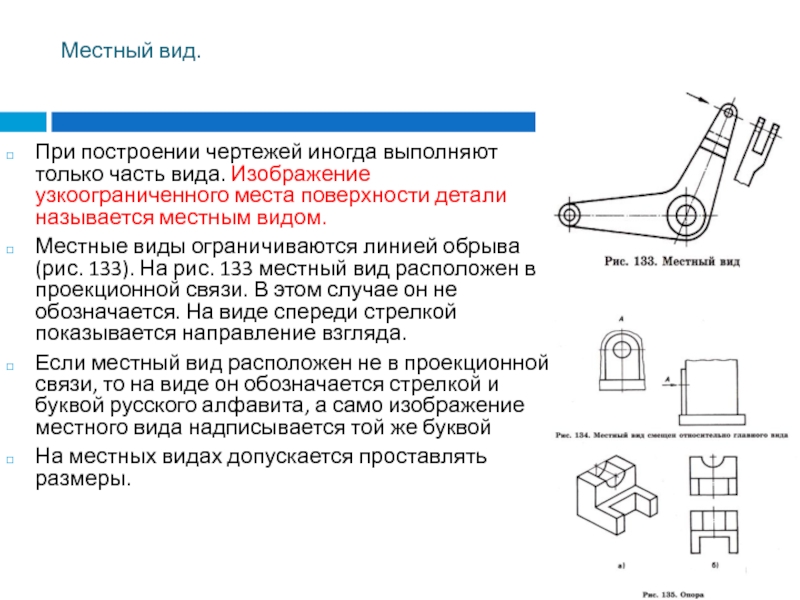
При построении чертежей иногда выполняют только часть вида. Изображение
узкоограниченного места поверхности детали называется местным видом.
Местные виды ограничиваются
линией обрыва (рис. 133). На рис. 133 местный вид расположен в проекционной связи. В этом случае он не обозначается. На виде спереди стрелкой показывается направление взгляда.
Если местный вид расположен не в проекционной связи, то на виде он обозначается стрелкой и буквой русского алфавита, а само изображение местного вида надписывается той же буквой
На местных видах допускается проставлять размеры.
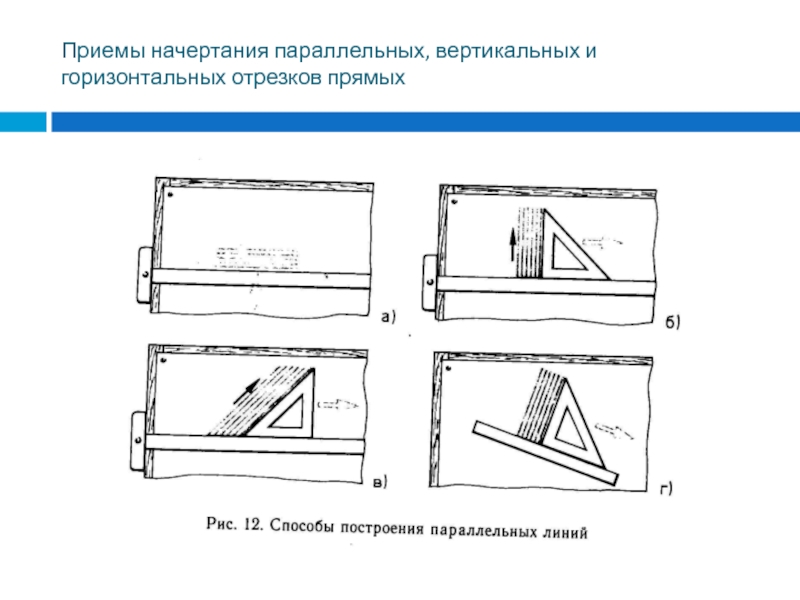
Слайд 42Приемы начертания параллельных, вертикальных и горизонтальных отрезков прямых
Слайд 43Билет 17
1 Соединение половины вида с половиной разреза.
2 Построение овала.
1
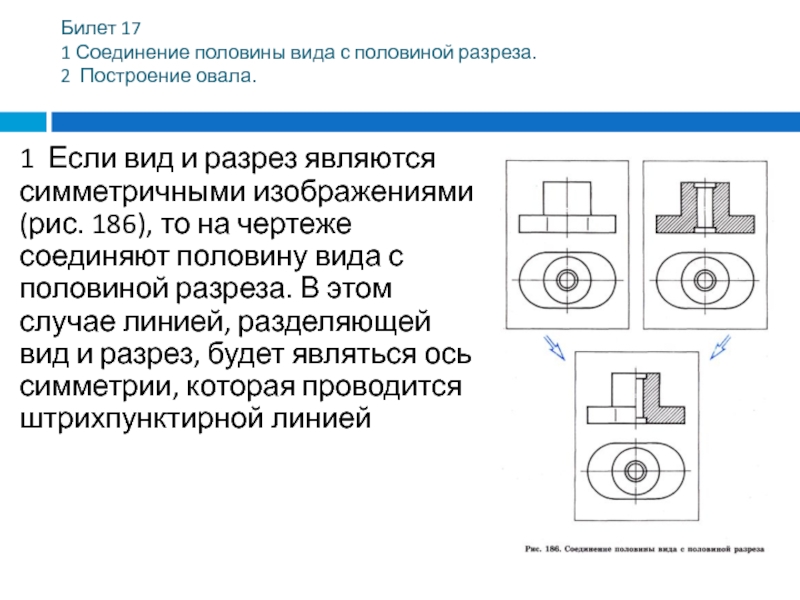
Если вид и разрез являются симметричными изображениями (рис. 186), то
на чертеже соединяют половину вида с половиной разреза. В этом случае линией, разделяющей вид и разрез, будет являться ось симметрии, которая проводится штрихпунктирной линией
Слайд 44Билет 18
1 Соединение части вида с частью разреза
2 Разъемные соединения
деталей
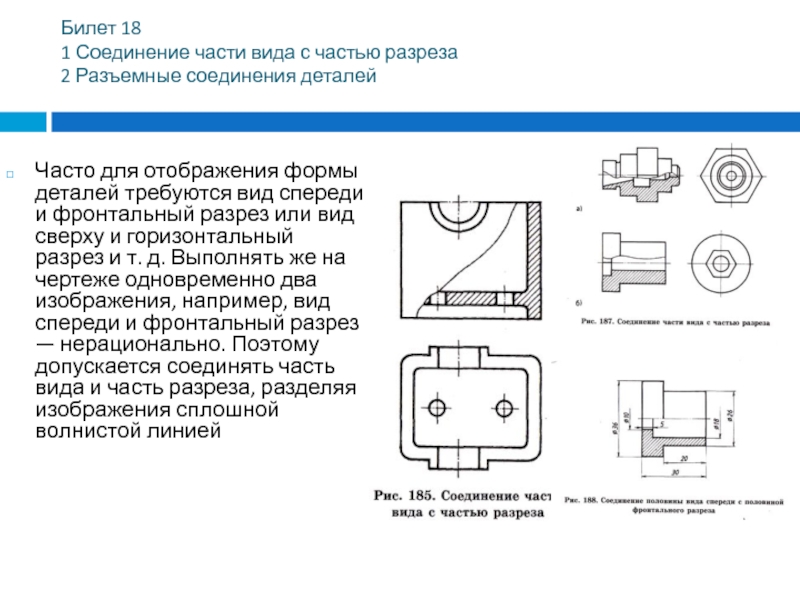
Часто для отображения формы деталей требуются вид спереди и фронтальный
разрез или вид сверху и горизонтальный разрез и т. д. Выполнять же на чертеже одновременно два изображения, например, вид спереди и фронтальный разрез — нерационально. Поэтому допускается соединять часть вида и часть разреза, разделяя изображения сплошной волнистой линией
Слайд 45Разъемные соединения деталей
К разъемным соединениям относятся такие соединения, которые допускают
многократную разборку и сборку без разрушения деталей и соединительных элементов,
входящих в них. К разъемным соединениям относятся резьбовые соединения (болтовые, винтовые, шпилечные), шлицевые или зубчатые, шпоночные и штифтовые (рис. 202). С помощью разъемных соединений можно осуществить разборку, настройку и ремонт изделия.
К разъемным соединениям относятся такие соединения, которые допускают многократную разборку и сборку без разрушения деталей и соединительных элементов, входящих в них. К разъемным соединениям относятся резьбовые соединения (болтовые, винтовые, шпилечные), шлицевые или зубчатые, шпоночные и штифтовые (рис. 202). С помощью разъемных соединений можно осуществить разборку, настройку и ремонт изделия.
Слайд 46Билет 19
1 Условности при построении разрезов.
2 Виды соединений детали.
В технике
часто можно встретить детали, содержащие такие конструктивные элементы, как тонкие
стенки, ребра жесткости, спицы. При изображении их в разрезах приняты следующие правила:
1. Если секущая плоскость проходит вдоль тонкой стенки, ребра жесткости, спицы, то на разрезе их показывают нерассеченными
2. Если секущая плоскость проходит поперек тонкой стенки, ребра жесткости, спицы, то на разрезе они показываются рассеченными
2 В сборочных единицах детали по-разному соединяются друг с другом. Соединение деталей в изделии может быть разъемным либо неразъемным.
Слайд 47Билет 20
1Местные разрезы
2 Неразъемные соединения.
Местный разрез.
Особым случаем соединения части вида
с частью разреза можно считать местный разрез. Местный разрез используется
для выявления внутренней формы предмета в отдельном, ограниченном месте. Для получения местного разреза небольшой по величине участок формы изделия мысленно удаляется. При этом секущая плоскость проходит вдоль оси отображаемого элемента (рис. 189, а).
На чертежах граница местного разреза показывается сплошной тонкой волнистой линией (рис. 189, б), которая не должна совпадать с какими-либо другими линиями изображения. Местный разрез на чертеже не обозначается.
Слайд 48Неразъемные соединения
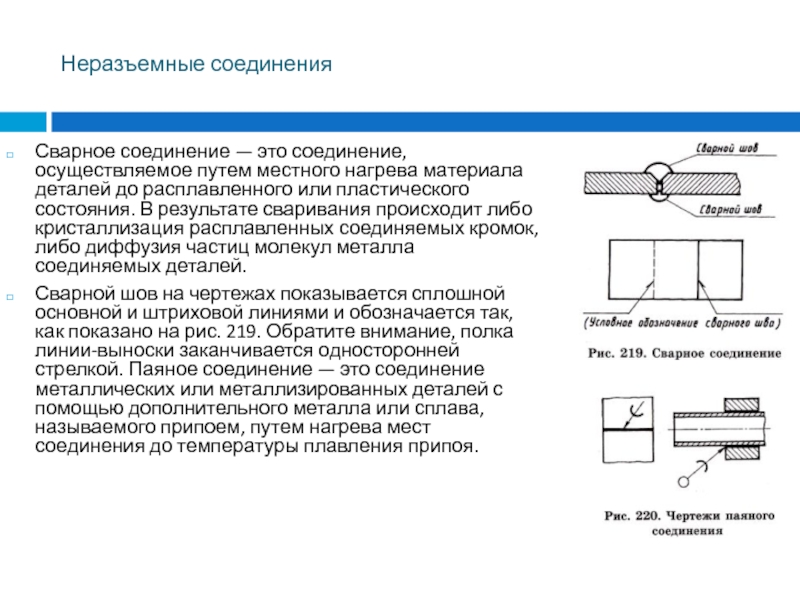
Сварное соединение — это соединение, осуществляемое путем местного нагрева
материала деталей до расплавленного или пластического состояния. В результате сваривания
происходит либо кристаллизация расплавленных соединяемых кромок, либо диффузия частиц молекул металла соединяемых деталей.
Сварной шов на чертежах показывается сплошной основной и штриховой линиями и обозначается так, как показано на рис. 219. Обратите внимание, полка линии-выноски заканчивается односторонней стрелкой. Паяное соединение — это соединение металлических или металлизированных деталей с помощью дополнительного металла или сплава, называемого припоем, путем нагрева мест соединения до температуры плавления припоя.
Слайд 49В соединениях, получаемых пайкой, место соединения элементов изображают на видах
и разрезах сплошной линией толщиной 2S. Для обозначения на
чертежах паяного соединения установлен знак в виде полуокружности .
Клепаное соединение представляет собой соединение двух деталей с помощью заклепки. На одном конце заклепки имеется головка, а другой — расклепывается.
Применяется в конструкциях, работающих под действием ударных и вибрационных нагрузок, а также для соединения деталей из металлов, плохо поддающихся сварке.
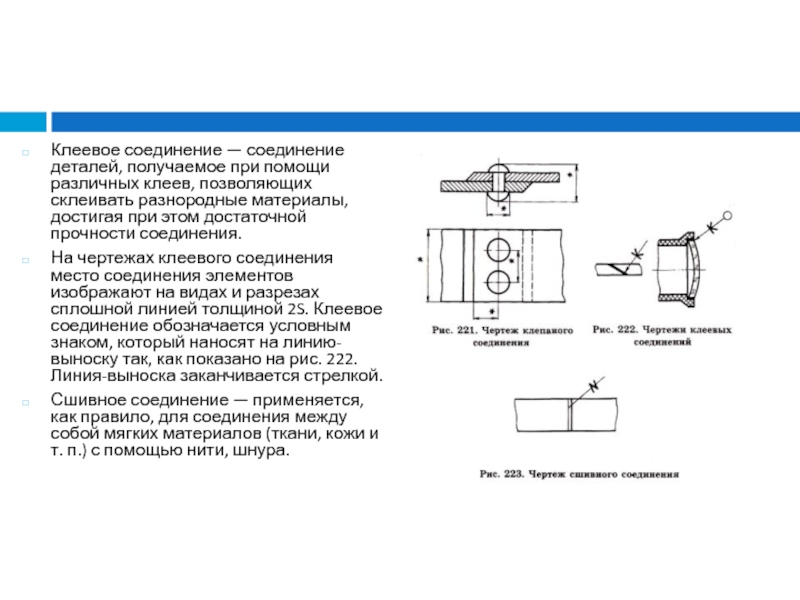
Слайд 50Клеевое соединение — соединение деталей, получаемое при помощи различных клеев,
позволяющих склеивать разнородные материалы, достигая при этом достаточной прочности соединения.
На
чертежах клеевого соединения место соединения элементов изображают на видах и разрезах сплошной линией толщиной 2S. Клеевое соединение обозначается условным знаком, который наносят на линию-выноску так, как показано на рис. 222. Линия-выноска заканчивается стрелкой.
Сшивное соединение — применяется, как правило, для соединения между собой мягких материалов (ткани, кожи и т. п.) с помощью нити, шнура.