Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Электромагнитные волны. Уравнения Максвелла и волновое уравнение
Содержание
- 1. Электромагнитные волны. Уравнения Максвелла и волновое уравнение
- 2. 1. Уравнения Максвелла и волновое уравнение.Рассмотрим однородную
- 3. 1. Уравнения Максвелла и волновое уравнение.Вычислим ротор
- 4. 1. Уравнения Максвелла и волновое уравнение.После вычисления
- 5. 1. Уравнения Максвелла и волновое уравнение.После вычисления
- 6. 1. Уравнения Максвелла и волновое уравнение.Сравним полученное
- 7. 1. Уравнения Максвелла и волновое уравнение.Решениями волнового
- 8. 1. Уравнения Максвелла и волновое уравнение.Вычислим ротор
- 9. 1. Уравнения Максвелла и волновое уравнение.Это уравнение
- 10. 1. Уравнения Максвелла и волновое уравнение.Фазовая скорость
- 11. 1. Уравнения Максвелла и волновое уравнение.Основные выводы:1.
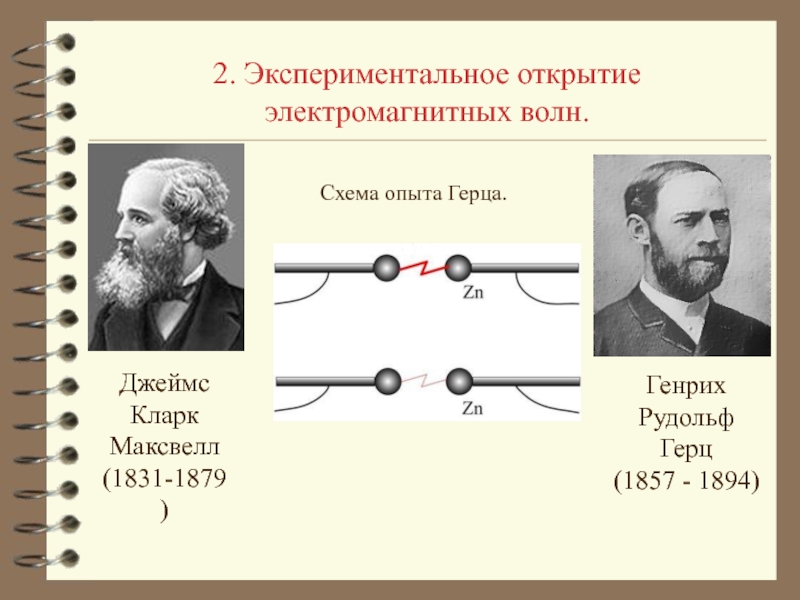
- 12. Экспериментальное открытие электромагнитных волн.2.
- 13. 2. Экспериментальное открытие электромагнитных волн.Схема опыта Герца.Джеймс Кларк Максвелл (1831-1879)
- 14. Поперечность электромагнитных волн.3.
- 15. 3. Поперечность ЭМВ. 1. Скорость распространения ЭМВ
- 16. 3. Поперечность ЭМВ.Если плоская ЭМВ распространяется вдоль
- 17. 3. Поперечность ЭМВ.ЭМВ распространяется вдоль оси OX,
- 18. 3. Поперечность ЭМВ.Рассмотрим уравнение, описывающее распространение ЭМВ:В левой части этого уравненияТо же по компонентам:
- 19. 3. Поперечность ЭМВ.
- 20. 3. Поперечность ЭМВ.Величина Ex, Ey, Ez зависит только от координаты x, поэтому
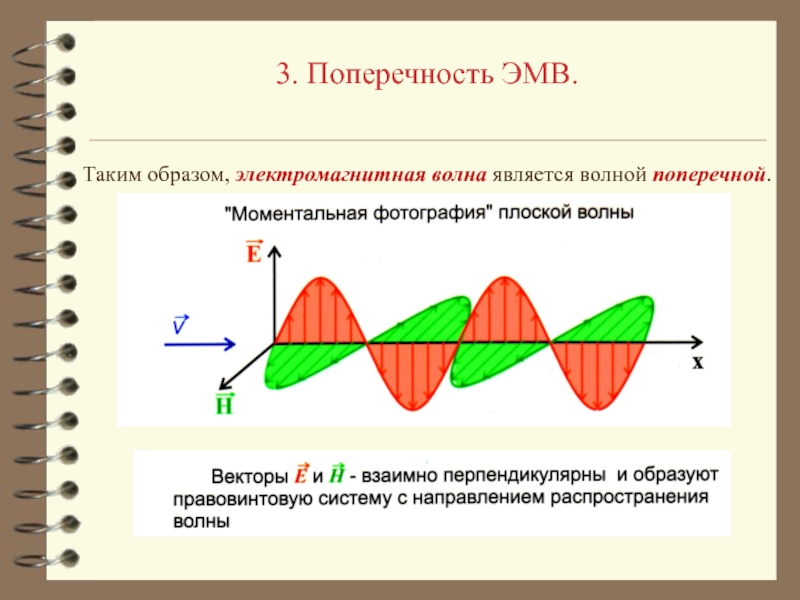
- 21. 3. Поперечность ЭМВ.В направлениях, перпендикулярных направлению распространения
- 22. 3. Поперечность ЭМВ.Если рассмотреть уравнение, описывающее распространение
- 23. 3. Поперечность ЭМВ.Таким образом, электромагнитная волна является волной поперечной.
- 24. Поляризация электромагнитных волн.4.
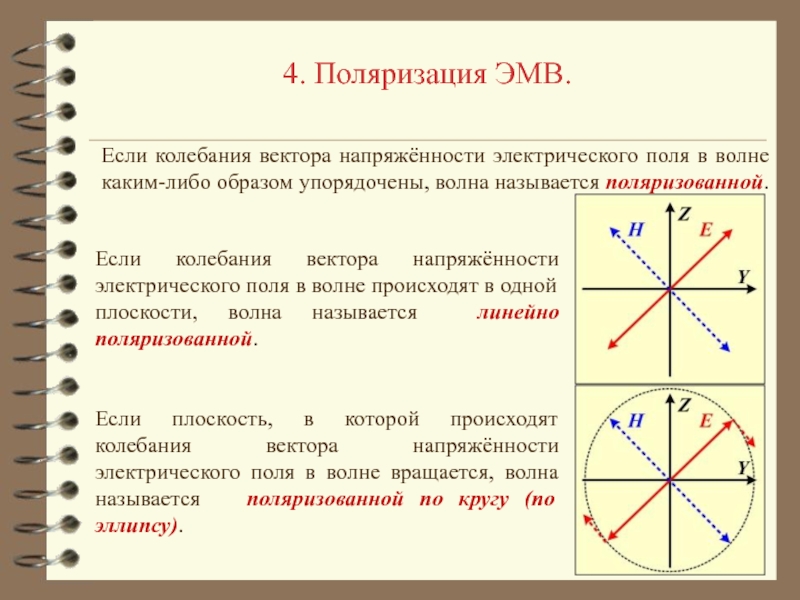
- 25. 4. Поляризация ЭМВ.Если колебания вектора напряжённости электрического
- 26. Соотношение между величинами E и H в электромагнитной волне.5.
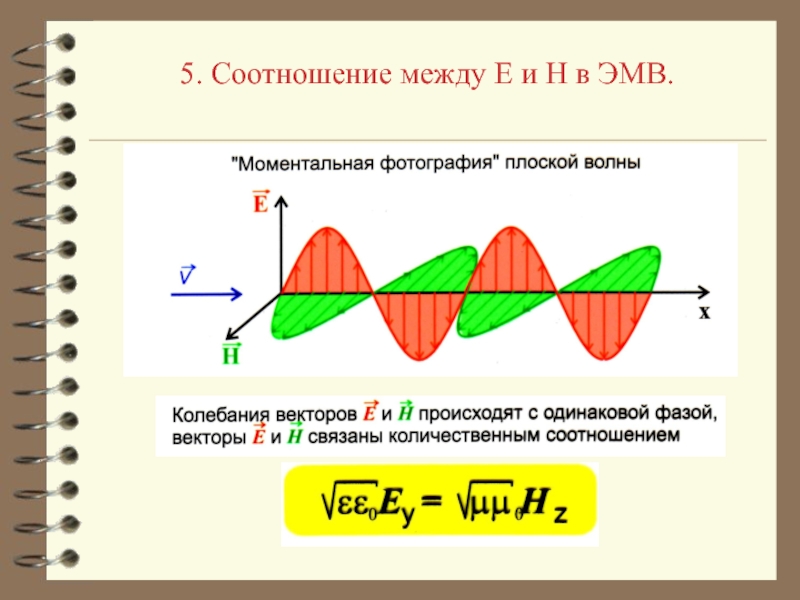
- 27. 5. Соотношение между E и H в ЭМВ.Рассмотрим уравнение, описывающее распространение ЭМВ:В левой части этого уравнения
- 28. 5. Соотношение между E и H в
- 29. 5. Соотношение между E и H в
- 30. 5. Соотношение между E и H в
- 31. 5. Соотношение между E и H в
- 32. 5. Соотношение между E и H в ЭМВ.
- 33. Вектор Умова-Пойнтинга.6.
- 34. 6. Вектор Умова-Пойнтинга.Известно, что плотность энергии электрического
- 35. 6. Вектор Умова-Пойнтинга.Если магнитная проницаемость постоянна,
- 36. 6. Вектор Умова-Пойнтинга.Аналогично преобразуем второе уравнение:Мы рассматриваем
- 37. 6. Вектор Умова-Пойнтинга.Из векторного анализа известно тождество:Применив это тождество, получим:
- 38. 6. Вектор Умова-Пойнтинга.Выясним физический смысл полученного выражения.
- 39. 6. Вектор Умова-Пойнтинга.Применим к левой части уравнения
- 40. 6. Вектор Умова-Пойнтинга.Таким образом, поток вектора Умова-Пойнтинга
- 41. Энергия, переносимая электромагнитной волной. 7.
- 42. 7. Энергия, переносимая электромагнитной волной. Известно, что
- 43. 7. Энергия, переносимая электромагнитной волной. Здесь v
- 44. 7. Энергия, переносимая электромагнитной волной. Введём новую
- 45. 7. Энергия, переносимая электромагнитной волной. Энергия электромагнитной
- 46. Скачать презентанцию
Слайды и текст этой презентации
Слайд 21. Уравнения Максвелла и волновое уравнение.
Рассмотрим однородную и изотропную, электрически
нейтральную, непроводящую среду.
Слайд 31. Уравнения Максвелла и волновое уравнение.
Вычислим ротор от правой и
левой части уравнения (1).
В рассматриваемой среде (ε = const.,
μ = const., σ = 0, ρ = 0) эти уравнения можно переписать так:(1)
(2)
(3)
(4)
Слайд 4
1. Уравнения Максвелла и волновое уравнение.
После вычисления ротора от левой
части уравнения (1) получаем:
Согласно уравнению (4)
Слайд 51. Уравнения Максвелла и волновое уравнение.
После вычисления ротора от правой
и левой части уравнения (1) получаем:
Согласно уравнению (3)
Вычислим ротор
от правой части уравнения (1). Слайд 61. Уравнения Максвелла и волновое уравнение.
Сравним полученное уравнение с общим
видом дифференциального волнового уравнения:
где v – фазовая скорость распространения
волны. Полученное нами уравнение для напряжённости электрического поля совпадает волновым уравнением, если
Решениями волнового уравнения являются плоские волны вида
Слайд 71. Уравнения Максвелла и волновое уравнение.
Решениями волнового уравнения для вектора
напряжённости электрического поля также являются плоские волны.
В данном случае в
пространстве распространяются колебания напряжённости электрического поля.Фазовая скорость распространения в пространстве таких колебаний:
Слайд 81. Уравнения Максвелла и волновое уравнение.
Вычислим ротор от правой и
левой части уравнения (3).
Аналогично можно вывести волновое уравнение, рассматривая
напряжённость магнитного поля. В рассматриваемой среде (ε = const., μ = const., σ = 0, ρ = 0):(1)
(2)
(3)
(4)
Выполним преобразования, как и в предыдущем случае, воспользуемся уравнением (2) и получим:
Слайд 91. Уравнения Максвелла и волновое уравнение.
Это уравнение можно переписать так:
где
- фазовая скорость волны.
- решение волнового уравнения, уравнение плоской
волны. Отметим, что решения одинаковы как для электрического поля, так и для магнитного. Колебания напряжённостей электрического и магнитного поле происходят одновременно и распространяются с одинаковой скоростью. Эти колебания совпадают по фазе.
Колебания напряжённостей электрического и магнитного полей, распространяющиеся в пространстве, называются электромагнитными волнами.
Слайд 101. Уравнения Максвелла и волновое уравнение.
Фазовая скорость электромагнитной волны
В
вакууме, когда ε = 1 и μ = 1,
В
некоторой среде, когда ε > 1 и μ > 1, В оптике величина n называется показателем преломления.
Физический смысл показателя преломления - он показывает, во сколько раз скорость света (ЭМВ) в данной среде меньше, чем в вакууме.
Слайд 111. Уравнения Максвелла и волновое уравнение.
Основные выводы:
1. Уравнения Максвелла допускают
волновые решения.
2. Электромагнитная полна представляет собой колебания напряженностей электрического и
магнитного полей, распространяющихся в пространстве.3. Скорость распространения ЭМВ в вакууме
4. Скорость распространения ЭМВ в любой диэлектрической среде меньше, чем в вакууме:
n – показатель преломления среды.
Слайд 132. Экспериментальное открытие электромагнитных волн.
Схема опыта Герца.
Джеймс Кларк Максвелл (1831-1879)
Слайд 153. Поперечность ЭМВ.
1. Скорость распространения ЭМВ в вакууме
2.
Скорость распространения ЭМВ в любой диэлектрической среде меньше, чем в
вакууме:n – показатель преломления среды.
Некоторые свойства ЭМВ мы уже отметили:
Ещё одним важнейшим свойством ЭМВ является её поперечность.
Слайд 163. Поперечность ЭМВ.
Если плоская ЭМВ распространяется вдоль оси OX выбранной
нами системы отсчёта, то её уравнение можно записать так:
Здесь ω
– циклическая (круговая) частота колебаний волны, k – волновое число.Известно, что волновые поверхности плоской волны - плоскости. Если волна распространяется вдоль оси OX, то её волновые поверхности есть плоскости, параллельные плоскости YZ (перпендикулярные OX).
Слайд 173. Поперечность ЭМВ.
ЭМВ распространяется вдоль оси OX, изменение векторов E
и H описывается уравнениями
Каждая из волновых поверхностей характеризуется одним значением
координаты X. Поэтому в пределах одной волновой поверхности в данный момент времени значения вектора напряжённости одинаковы. Это справедливо и для вектора E и для вектора H.Значения всех трёх компонент вектора E и всех трёх компонент вектора H зависят только от координаты X и не зависят от координат Y и Z.
Слайд 183. Поперечность ЭМВ.
Рассмотрим уравнение, описывающее распространение ЭМВ:
В левой части этого
уравнения
То же по компонентам:
Слайд 213. Поперечность ЭМВ.
В направлениях, перпендикулярных направлению распространения волны, производные по
времен от H нулю не равны, следовательно, в этих направлениях
может существовать переменное магнитное поле. В направлении, параллельном направлению распространения волны, может существовать только стационарное магнитное поле.Слайд 223. Поперечность ЭМВ.
Если рассмотреть уравнение, описывающее распространение ЭМВ
и, как и
в предыдущем случае, переписать его в виде проекций на оси
координат, и учесть, что все компоненты вектора H зависят только от координаты x, получимВ направлениях, перпендикулярных направлению распространения волны, может существовать переменное электрическое поле. В направлении, параллельном направлению распространения волны, может существовать только стационарное электрическое поле.
Слайд 254. Поляризация ЭМВ.
Если колебания вектора напряжённости электрического поля в волне
каким-либо образом упорядочены, волна называется поляризованной.
Если колебания вектора напряжённости электрического
поля в волне происходят в одной плоскости, волна называется линейно поляризованной.Если плоскость, в которой происходят колебания вектора напряжённости электрического поля в волне вращается, волна называется поляризованной по кругу (по эллипсу).
Слайд 275. Соотношение между E и H в ЭМВ.
Рассмотрим уравнение, описывающее
распространение ЭМВ:
В левой части этого уравнения
Слайд 285. Соотношение между E и H в ЭМВ.
Учтём, что вектор
E зависит только от координаты x
Рассмотрим уравнение, описывающее распространение ЭМВ:
В
левой части этого уравненияСлайд 295. Соотношение между E и H в ЭМВ.
Учтём, что вектор
H зависит только от координаты x
Решениями волнового уравнения являются плоские
волны(волна распространяется вдоль OX, векторы напряжённостей перпендикулярны)
Слайд 305. Соотношение между E и H в ЭМВ.
Как мы установили
ранее,
Подставим в это уравнение выражения дл напряжённостей полей.
Это соотношение должно
выполняться в любой момент времени и в точке с любой координатой x. Слайд 315. Соотношение между E и H в ЭМВ.
Волновое число k
связано с циклической частотой ω соотношением
Слайд 346. Вектор Умова-Пойнтинга.
Известно, что плотность энергии электрического поля
Эти выражения можно
получить из уравнений Максвелла. Рассмотрим уравнения:
а плотность энергии магнитного
поля(1)
(2)
Умножим уравнение (1) на вектор H скалярно, а уравнение (2) умножим скалярно на вектор E.
Слайд 366. Вектор Умова-Пойнтинга.
Аналогично преобразуем второе уравнение:
Мы рассматриваем непроводящую среду, поэтому
j = 0.
Итого, мы получили два уравнения:
Вычтем из второго уравнения
первое:Слайд 376. Вектор Умова-Пойнтинга.
Из векторного анализа известно тождество:
Применив это тождество, получим:
Слайд 386. Вектор Умова-Пойнтинга.
Выясним физический смысл полученного выражения. Обозначим
Преобразуем левую часть
уравнения:
- плотность энергии электромагнитного поля.
- вектор Умова-Пойнтинга.
Слайд 396. Вектор Умова-Пойнтинга.
Применим к левой части уравнения теорему Остроградского-Гаусса:
Здесь Ω
- поверхность, окружающая объём V.
Чтобы равенство не нарушилось, вычислим
интеграл по объёму V и в правой части:Здесь Wэм - энергия электромагнитного поля в объёме V.
Итого, получилось:
Слайд 406. Вектор Умова-Пойнтинга.
Таким образом, поток вектора Умова-Пойнтинга через некоторую замкнутую
поверхность равен убыли энергии электромагнитного поля в объёме, ограниченном этой
замкнутой поверхностью.Согласно определению,
Таким образом,
Эти векторы образуют правую тройку.
E и H лежат в плоскости, перпендикулярной направлению распространения волны, направление S совпадает с направлением распространения волны.
Слайд 427. Энергия, переносимая электромагнитной волной.
Известно, что плотность энергии электромагнитного
поля
Если в пространстве распространяется электромагнитная волна, то в данной точке
пространстваПлотность энергии магнитного поля
В любой момент времени
Слайд 437. Энергия, переносимая электромагнитной волной.
Здесь v – скорость электромагнитной
волны в данной среде. В вакууме, когда v = c,
В
некоторой средеСлайд 447. Энергия, переносимая электромагнитной волной.
Введём новую величину, S, и
назовём её модулем плотности потока энергии. То есть эта величина
будет равна энергии, проходящей через единицу площади в единицу времениW – энергия, Ω - площадь, t – время.
Модуль плотности потока энергии (эта величина равна энергии, проходящей через единицу площади в единицу времени) равен модулю вектора Умова – Пойнтинга.