Слайд 2Эйлеровы циклы и пути
Эйлеровым путем в графе называется произвольный путь,
проходящий через каждое ребро графа в точности один раз, т.е.
путь v1, ..., vm+1, такой что каждое ребро e E появляется в последовательности v1, ..., vm+1 в точности один раз как e = {vi, vi+1 } для некоторого i.
Если v1 = vm+1, то такой путь называется эйлеровым циклом. Задача существования эйлерова пути в заданном графе была решена Эйлером в 1736 году, и представленное им необходимое и достаточное условие существования такого пути считается первой в истории теоремой теории графов.
Теорема. Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более чем две вершины нечетной степени.
Слайд 3Как определить связен ли граф?
Существует много алгоритмов на графах, в
основе которого лежит систематический перебор вершин, такой что каждая вершина
просматривается в точности один раз.
Метод поиска будем считать «хорошим», если
он позволяет алгоритму легко «погрузиться» в этот метод и
каждое ребро графа анализируется не более одного раза (или число раз, ограниченное константой)
Слайд 4Поиск в глубину в графе (depth first search)
procedure DFS(v)
(*поиск в
глубину из вершины v ;
переменные НОВЫЙ, ЗАПИСЬ глобальные *)
begin
рассмотреть v; НОВЫЙ[v]:= ложь;
for u ЗАПИСЬ [v] do
if НОВЫЙ[u] then DFS(u)
end (* вершина v использована *)
Слайд 5Поиск в глубину в произвольном, необязательно связном графе, проводится согласно
следующему алгоритму:
begin
for v V do НОВЫЙ[v]:=
истина;
for v V do
if НОВЫЙ[v] then DFS(v)
end
Алгоритм просматривает каждую вершину в точности один раз и его сложность порядка O(n + m)
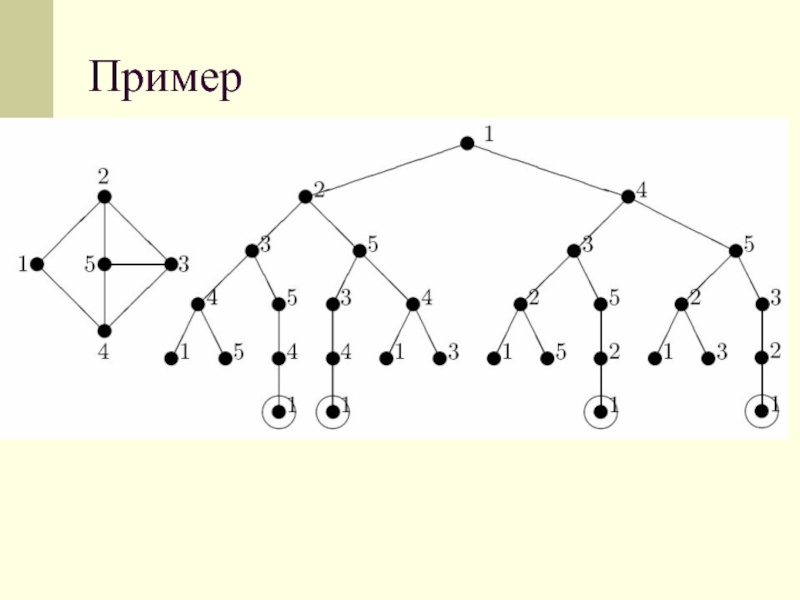
Слайд 6Алгоритм нахождения эйлерова цикла
Исходные данные: связный граф G = V, E без вершин
нечетной степени, представленный списками ЗАПИСЬ [v], v V.
Результаты: Эйлеров
цикл, представленный последовательностью вершин в стеке СЕ.
Слайд 7begin
CTEK := ; СЕ := ;
v:= произвольная вершина графа;
CTEK v;
while CTEK do
begin v:= top (CTEK); { v = верхний элемент стека }
if ЗАПИСЬ [v] then
begin u:= первая вершина списка ЗАПИСЬ [v];
CTEK u;
{ удалить ребро {v, u} из графа }
ЗАПИСЬ [v] := ЗАПИСЬ [v] \ {u};
ЗАПИСЬ [u] := ЗАПИСЬ [u] \ {v};
v := u
end
else { ЗАПИСЬ [v] = }
begin v CTEK ; СЕ v;
end
end
end
Слайд 8Вычислительная сложность алгоритма Эйлера
каждая итерация главного цикла либо помещает вершину
в стек CTEK и удаляет ребро из графа, либо переносит
вершину из стека CTEK в стек CE. Таким образом, число итераций этого цикла — О(m). В свою очередь число шагов в каждой итерации ограничено константой.
Т.о. общая сложность алгоритма есть О(m).
Слайд 9Эйлеровы пути
Если в связном графе нет вершин нечетной степени, то
каждый эйлеров путь является циклом, так как концы эйлерова пути,
не являющегося циклом, всегда вершины нечетной степени.
Предположим, что u и v — единственные вершины нечетной степени связного графа G = V, E, и образуем граф G* добавлением дополнительной вершины t и ребер {u, t} и {v, t} (или просто {u, v}, если {u, v} E ). Тогда G* — связный граф без вершин нечетной степени, а эйлеровы пути в G будут в очевидном взаимно однозначном соответствии с эйлеровыми циклами в G*.
Слайд 10Гамильтоновы пути и циклы
гамильтоновым называется путь, проходящий в точности
один раз через каждую вершину (а не каждое ребро) данного
графа.
В отличие от эйлеровых путей не известно ни одного простого необходимого и достаточного условия для существования гамильтоновых путей и это несмотря на то, что эта задача — одна из самых центральных в теории графов.
Не известен также алгоритм, который проверял бы существование гамильтонова пути в произвольном графе, используя число шагов, ограниченное многочленом от переменной n (числа вершин в графе).
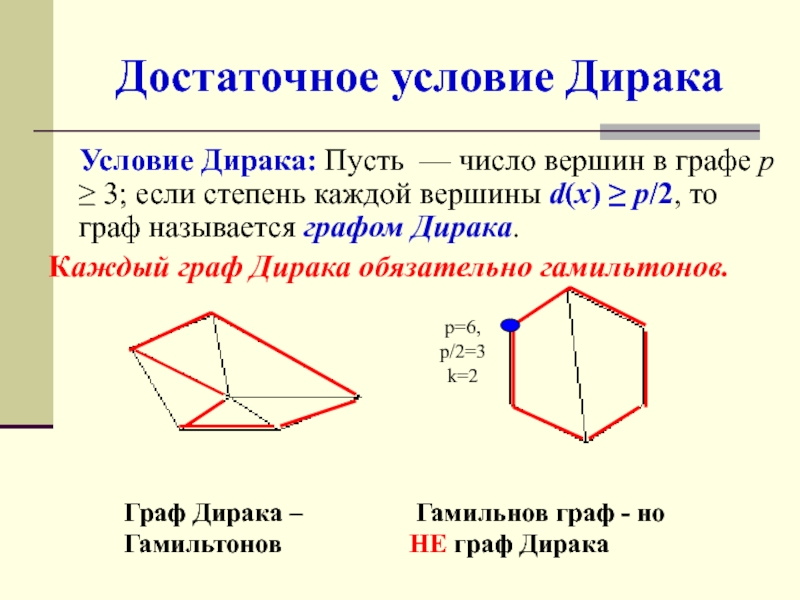
Слайд 11Достаточное условие Дирака
Условие Дирака: Пусть — число вершин
в графе р ≥ 3; если степень каждой вершины d(x)
≥ р/2, то граф называется графом Дирака.
Каждый граф Дирака обязательно гамильтонов.
Граф Дирака – Гамильнов граф - но
Гамильтонов НЕ граф Дирака
p=6,
p/2=3
k=2
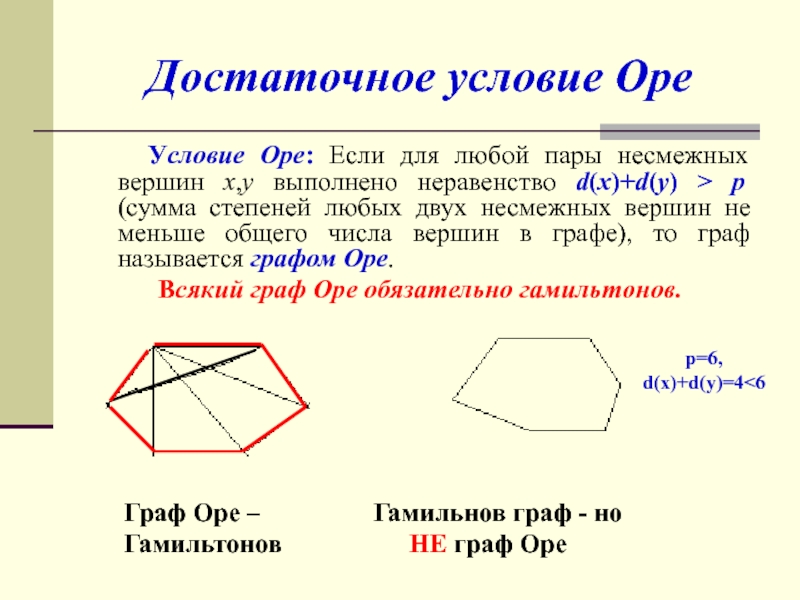
Слайд 12Достаточное условие Оре
Условие Оре: Если для любой пары
несмежных вершин x,y выполнено неравенство d(x)+d(y) > p (сумма степеней
любых двух несмежных вершин не меньше общего числа вершин в графе), то граф называется графом Оре.
Всякий граф Оре обязательно гамильтонов.
Граф Оре – Гамильнов граф - но
Гамильтонов НЕ граф Оре
p=6,
d(x)+d(y)=4<6
Слайд 13Достаточное условие Поша
Введем функцию Поша f(x) целого неотрицательного аргумента x,
такую что функция f(x) в каждом целом неотрицательном х принимает
значение, равное количеству вершин графа, степень которых не превосходит х. Функция Поша следующего графа:
Графом Поша называется граф , удовлетворяющий условиям
1) для 1 х < (p – 1)/2 выполняется неравенство f(x) 2) если (p-1)/2 - целое число, то при x=(p-1)/2 имеет место f(x)<(p-1)/2
Каждый граф Дирака и граф Оре – граф Поше
Каждый граф Поша обязательно гамильтонов. Простой цикл на большом числе вершин графом Поша не является, но, конечно, является гамильтоновым графом.
Слайд 14Двусвязные графы
Сочленение – вершина, удаление которой увеличивает число компонент связности
графа.
Двусвязный граф – связанный граф не содержащий сочленений
Теорема: Каждый
гамильтонов граф двусвязен. Каждый негамильтонов двусвязный граф содержит тета-подграф.
Тета-подграф — это блок, содержащий только вершины степени 2 и две несмежные вершины степени 3.
Слайд 17NP–полные задачи
NP-полные задачи — это класс задач, лежащих в классе NP
(то есть для которых пока не найдено быстрых алгоритмов решения,
но проверка того, является ли данное решение правильным, проходит быстро).
Ни для одной из NP-полных задач не известен полиномиальный алгоритм (т.е. с числом шагов, ограниченным полиномом от размерности задачи), причем существование полиномиального алгоритма для хотя бы одной из них автоматически влекло бы за собой существование полиномиальных алгоритмов для всех этих задач.
Слайд 18Задача существования гамильтонова пути
алгоритм «в лоб» — это полный
перебор всех возможностей: генерируем все n! различных последовательностей вершин и
для каждой из них проверяем, определяет ли она гамильтонов путь. Такие действия требуют по меньшей мере n! n шагов, но функция от n подобного вида растет быстрее, чем произвольный многочлен, и даже быстрее, чем произвольная экспоненциальная функция вида an, a > 1, ибо
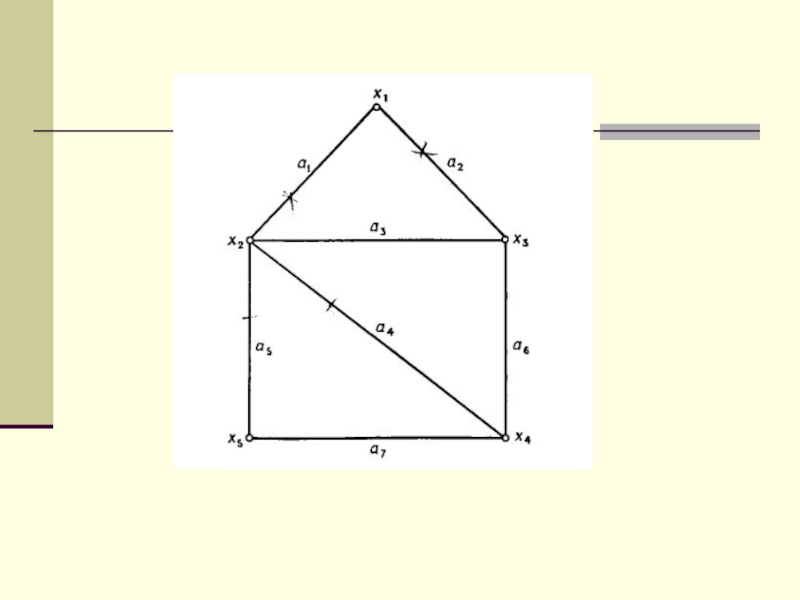
Слайд 19Алгоритм с возвратом (backtracking)
Данные: Граф G = V, E, представленный списками инцидентности ЗАПИСЬ[v],
v V.
Результаты: Список всех гамильтоновых циклов графа G.
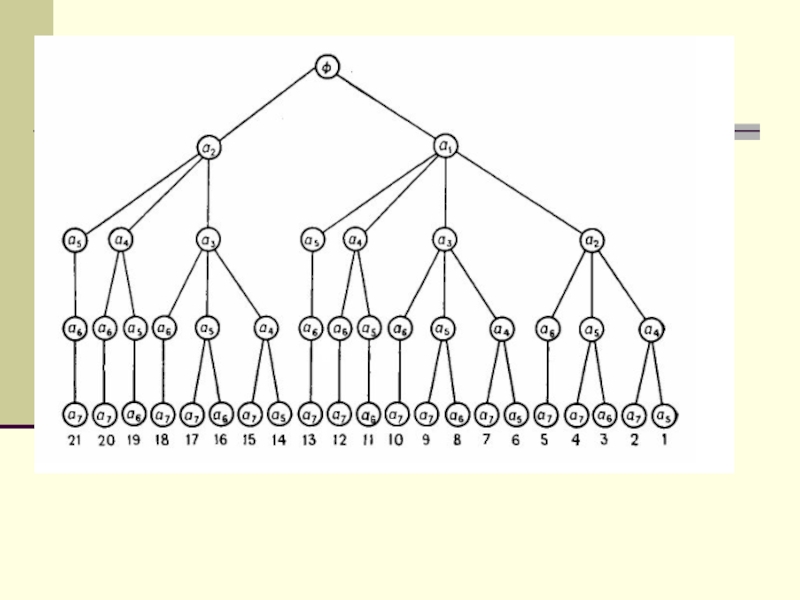
Слайд 20procedure ГАМИЛЬТ(k)
{генерация всех гамильтоновых циклов, являющихся расширением
последовательности X[1], . . ., X[k – 1]: массив
X — глобальный }
begin
for y ЗАПИСЬ [X[k – 1]] do
if (k = n +1) and (y = v0) then write(X[1], . . ., X[n], v0)
else if DOP[y] then
begin X[k] := y; DOP[y] := ложь;
ГАМИЛЬТ (k +1);
DOP[y] := истина
end
end; { ГАМИЛЬТ }
begin { главная программа }
for v V do DOP[v] := истина; { инициализация }
X[1] := v0; { v0 = произвольная фиксированная вершина графа }
DOP[v0] := ложь;
ГАМИЛЬТ (2);
end.
Слайд 22!!!! для большинства приложений число шагов алгоритма с возвратом хотя
и будет меньше, чем в случае полного перебора, однако же
в наихудшем случае растет по экспоненте с возрастанием размерности задачи.
Слайд 23Задача коммивояжера
Коммивояжер должен совершить поездку по городам и вернуться обратно,
побывав в каждом городе ровно один раз, сведя при этом
затраты на передвижение к минимуму.
Для решения задачи нам необходимо найти гамильтонов цикл минимального общего веса.
Эффективный алгоритм пока не известен. Для сложных сетей число гамильтоновых циклов непомерно велико. Рассмотрим алгоритм поиска субоптимального решения.
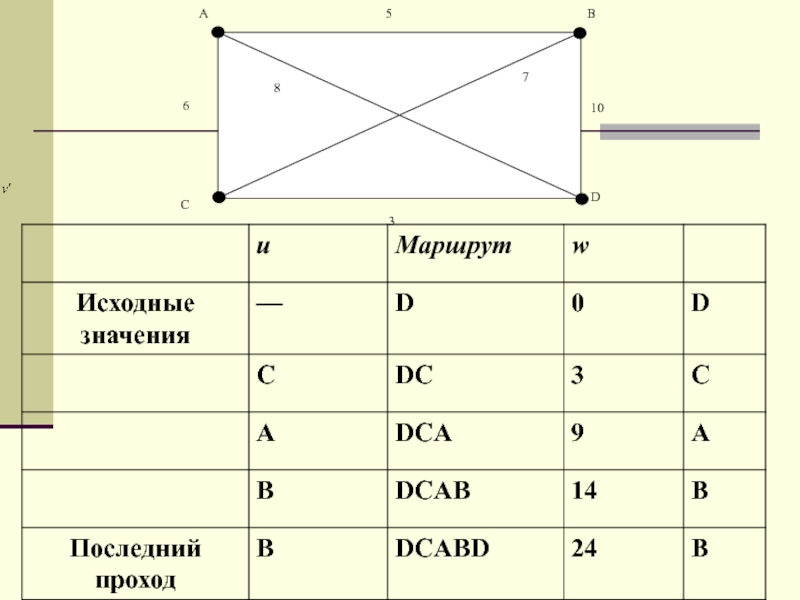
Алгоритм ближайшего соседа
Дан нагруженный граф с множеством вершин V. Цикл, полученный в результате работы, будет совпадать с конечным значением переменной маршрут, а его длина — конечное значение переменной w.
Слайд 24Begin
Выбрать v V;
Маршрут := v;
w:=
0;
v:=v;
Отметить v;
while останутся
неотмеченные вершины do
begin
Выбрать неотмеченную вершину u, ближайшую к v;
Маршрут := маршрут и;
w:= w + вес ребра v u;
v := u;
Отметить v
еnd
Маршрут := маршрут v;
w:= w + вес ребра v v
end
Слайд 26!!! В полном графе с 20-ю вершинами существует приблизительно 6,1*1016
гамильтононовых циклов
Слайд 27Деревья
Граф G = V, E называется деревом, если он
связен и ацикличен.
Пусть G = V, E — граф
с n вершинами и m ребрами.
Необходимые и достаточные условия того, что G — дерево:
Любая пара вершин в G соединена единственным путем
G связен и m = n – 1
G связен и удаление хотя бы одного его ребра нарушает связность графа
G ацикличен, но если добавить хотя бы одно ребро, то в G появится цикл.
Слайд 28Остовной граф
В любом связном графе найдется подграф, являющийся деревом.
Подграф в
G, являющийся деревом и включающий в себя все вершины G,
называется остовным деревом.
Построение остовного дерева: Выбираем произвольное ребро и последовательно добавляем другие ребра, не создавая при этом циклов, до тех пор, пока нельзя будет добавить никакого ребра, не получив при этом цикла.
! Всего n -1 ребро!!!
Слайд 32Алгоритм построения минимального остовного дерева (задача поиска кратчайшего соединения)
Задача построения
минимального остовного дерева — это одна из немногих задач теории
графов, которую можно считать полностью решенной.
Задача о проведении дорог. Для каждой пары городов А и В известна стоимость С(А,В) строительства городов между ними. Нужно построить самую дешевую из все возможных сеть дорог. Искомый граф должен быть деревом, которое называют экономическим. Таким образом, задача состоит в нахождении алгоритма, определяющего среди nn–2 возможных деревьев, которые соединяют вершины, дерева наименьшей длины, определяемой как сумма его ребер.
Слайд 33Алгоритм Крускала
Пусть есть связный граф, имеющий n вершин.
Шаг 1.
Упорядочим ребра графа в порядке их неубывания их весов.
Шаг 2.
Начиная с первого ребра в этом списке, добавлять ребра в графе, соблюдая условие: такое добавление не должно приводить к появлению цикла.
Шаг 3. Повторять Шаг 2 до тех пор, пока число ребер в графе не станет равно n – 1. Получившееся дерево является минимальным остовным деревом графа.
Больше всего времени необходимо для выполнения сортировки — при m ребрах это m log2m операций. Но нужны только n – 1 ребро!
Для полных графов более эффективный алгоритм был предложен Примом и Дейкстрой.
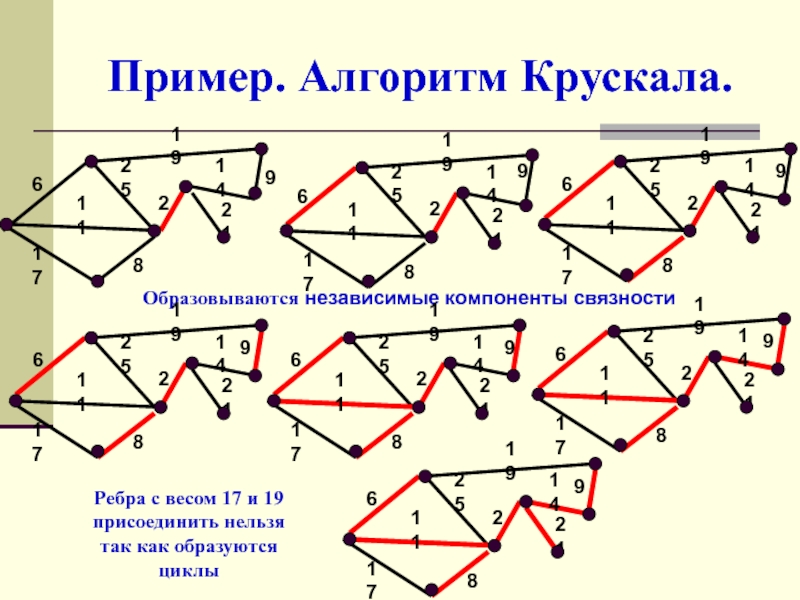
Слайд 34Пример. Алгоритм Крускала.
Образовываются независимые компоненты связности
11
8
6
9
19
2
14
21
17
25
11
8
9
19
2
14
21
17
25
11
8
6
19
2
14
21
17
25
11
8
6
19
2
14
21
17
25
11
8
6
19
2
14
21
17
25
6
9
9
9
11
8
6
19
2
14
21
17
25
9
11
8
6
19
2
14
21
17
25
9
Ребра с весом 17 и
19
присоединить нельзя
так как образуются циклы
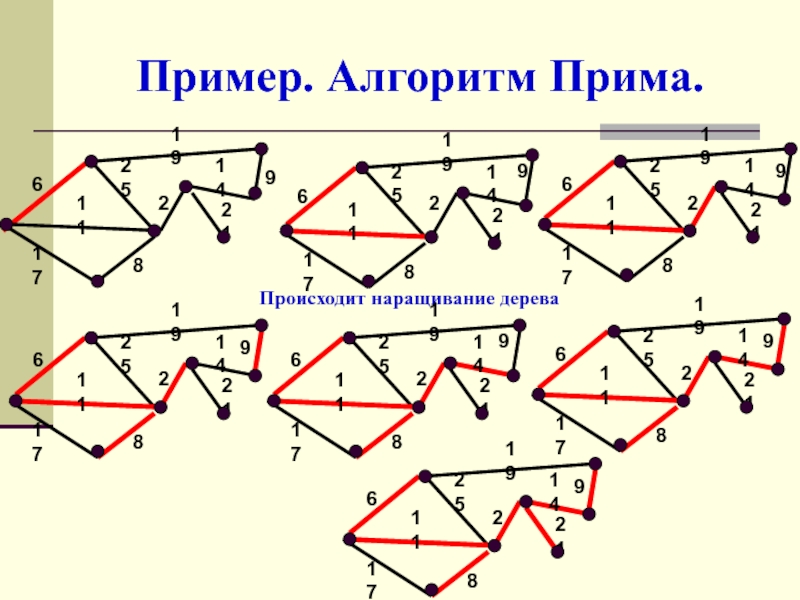
Слайд 35Алгоритм Прима
Шаг 1. Выбрать произвольную вершину и ребро, соединяющее ее
с ближайшим по весу соседом.
Шаг 2. Найдите не присоединенную (еще)
вершину, ближе всего лежащую к одной из присоединенных, и соедините с ней.
Шаг 3. Повторять Шаг 2 до тех пор, пока все вершины не будут присоединены.
Слайд 36Пример. Алгоритм Прима.
Происходит наращивание дерева
11
8
6
9
19
2
14
21
17
25
11
8
9
19
2
14
21
17
25
11
8
6
19
2
14
21
17
25
11
8
6
19
2
14
21
17
25
11
8
6
19
2
14
21
17
25
6
9
9
9
11
8
6
19
2
14
21
17
25
9
11
8
6
19
2
14
21
17
25
9





![Элементы теории графов Алгоритм нахождения эйлерова циклаИсходные данные: связный граф G = V, E без вершин нечетной Алгоритм нахождения эйлерова циклаИсходные данные: связный граф G = V, E без вершин нечетной степени, представленный списками ЗАПИСЬ [v], v](/img/thumbs/66d6222e43a265230cdd5c1441f77006-800x.jpg)








![Элементы теории графов Алгоритм с возвратом (backtracking)Данные: Граф G = V, E, представленный списками инцидентности ЗАПИСЬ[v], v Алгоритм с возвратом (backtracking)Данные: Граф G = V, E, представленный списками инцидентности ЗАПИСЬ[v], v V.Результаты: Список всех гамильтоновых циклов](/img/thumbs/8ff9892fb924209324bceb11c92d4662-800x.jpg)
![Элементы теории графов procedure ГАМИЛЬТ(k){генерация всех гамильтоновых циклов, являющихся расширением последовательности procedure ГАМИЛЬТ(k){генерация всех гамильтоновых циклов, являющихся расширением последовательности X[1], . .](/img/thumbs/b6fc993b189aeebcc34ea021e27d0d35-800x.jpg)