Филипп Алексеевич Барон, PhD 2 марта 2020 Измерение малых расстояний в

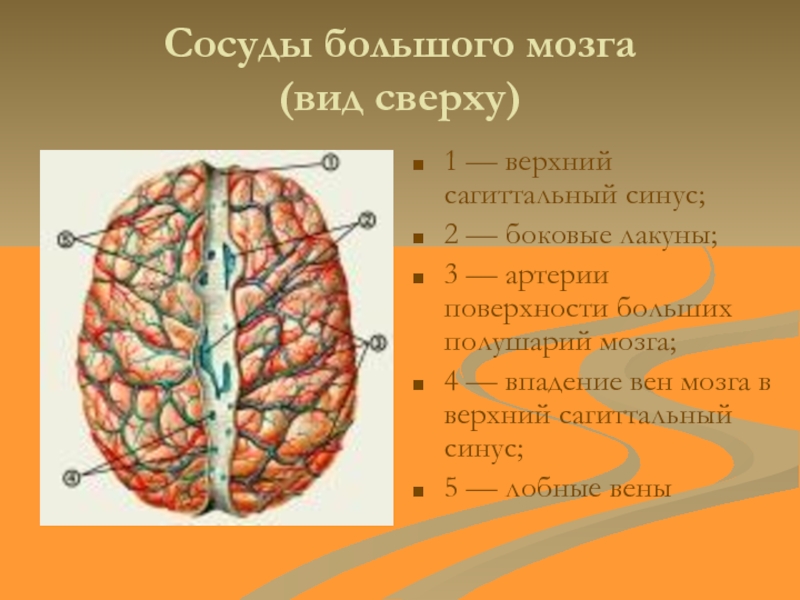
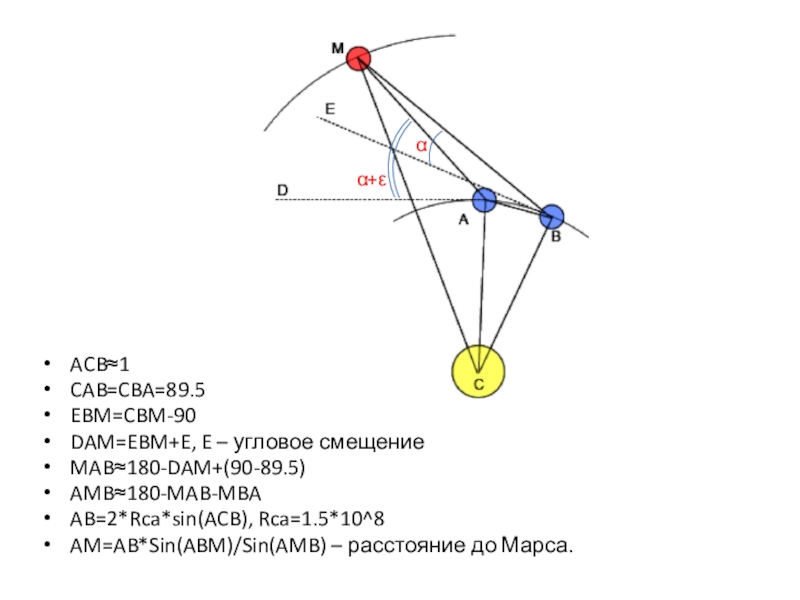
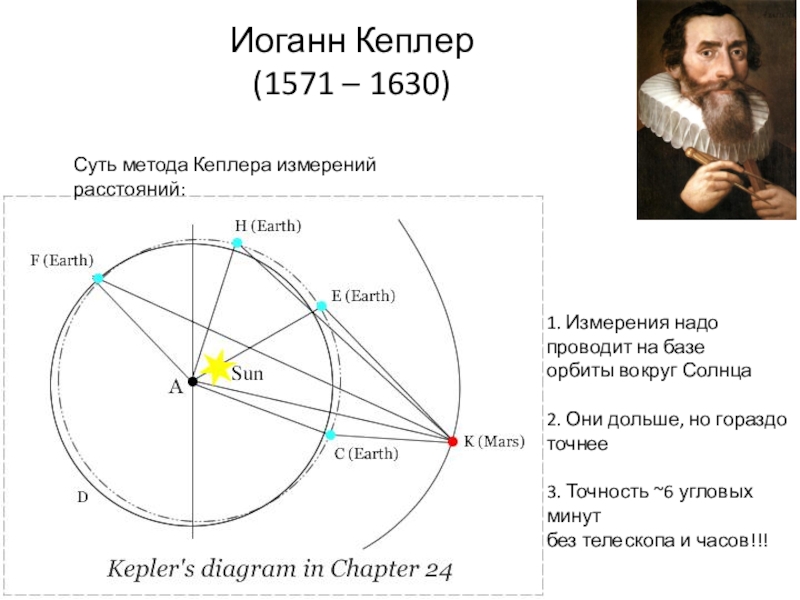
неё являются вертикальный и горизонтальный углы, расстояние Земля-Солнце, на выходе

мы получаем расстояние до Марса.
Этот метод годится не только для расчётов Марса, таким образом можно измерить расстояние до Венеры, Юпитера и Сатурна
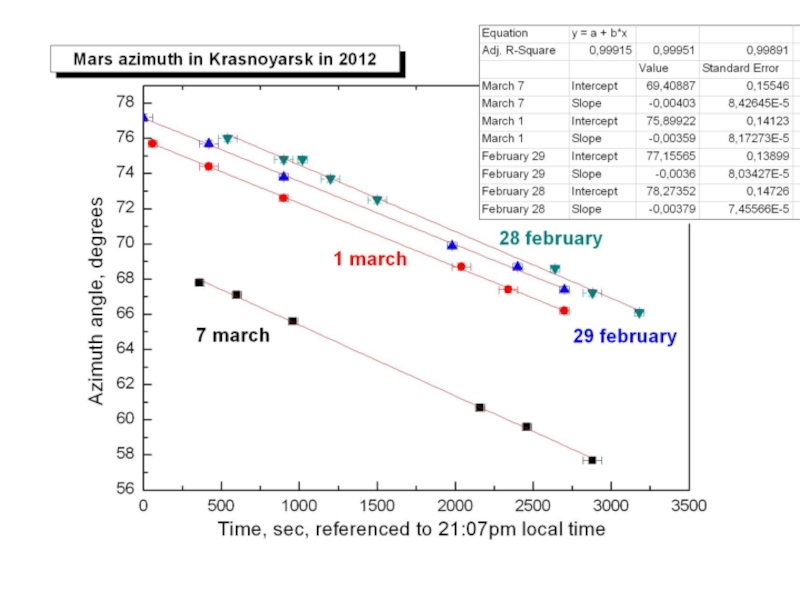
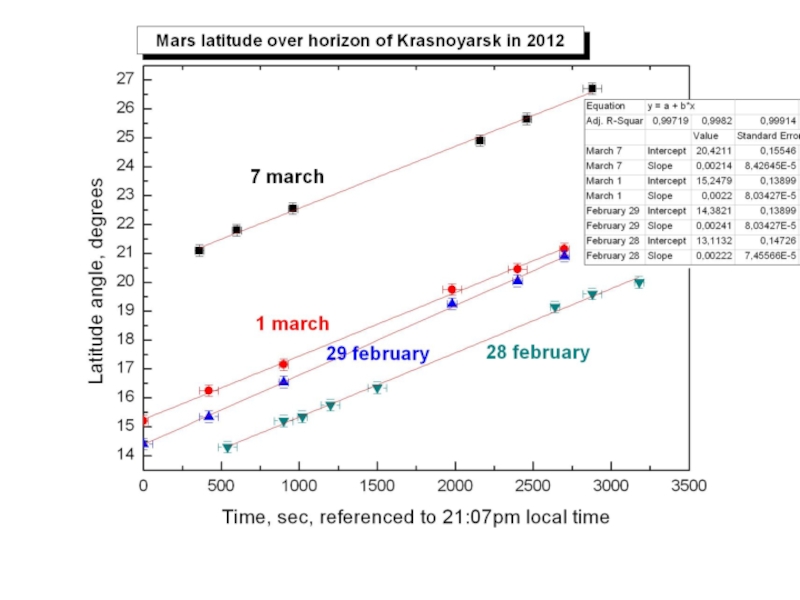
Вычисленное нами расстояние было равно 1.23*108, когда на тот момент расстояние до Марса было 1.07*108.
Это произошло из-за собственного движения Марса по своей орбите – в нашей модели движение Марса не учитывалось. Расчёт расстояния с учётом смещения планеты требует более сложных математических вычислений, но это возможно

ученого Аристарха (3 в. д. н. э.) найти расстояние до

Солнца

 Можно выразить расстояние до Солнца в единицах расстояния до Луны

 При этом нужно выразить расстояние до Луны в единицах радиуса Земли

Эратосфен вычисляет радиус Земли

2 в. д. н. э., то есть через целых 100

лет!

Взяв из таблицы хорд ее значения для альфы и бетты, а также значение для радиуса Земли
от Эратосфена и подставив их в эту формулу, Гипарх нашел, что расстояние для Луны
приблизительно равно 59 Земных радиусов, то есть примерно 240 тысяч километров

Так родился метод параллакса

Задача: зная радиус Земли и углы,
- найти расстояние до Луны

используем для решения этой задачи гораздо более удобную современную функцию

– синус:

Но на изобретение синуса потребовалось еще 1500 лет!

малайамском языке. Основные результаты:

Гипарха Никейского, т.е. ночного параллакса Луны
2. Из полученного угла параллакса

β вычесть
ночное смещение Луны из-за ее движения по
орбите вокруг Земли, исходя из пропорции:

360 градусов Луна проходит за 29.5 дней = 29.5*24 = 708часов
Х градусов Луна проходит за время между часовыми поясами Пацанов,
либо между временем вечернего и утреннего измерений Гипарха

Но у Гипарха не было точных часов!!!
=> 240 тысяч километров вместо 380тыс

Нужен был более точный метод определения расстояний до небесных тел,
имея «неточные часы» и БЕЗ ТЕЛЕСКОПА

на базе
орбиты вокруг Солнца

2. Они дольше, но гораздо
точнее

3. Точность

~6 угловых минут
без телескопа и часов!!!

точные часы и,
имея в распоряжении телескопы …
В 1671-1677 годах с

помощью измерений затмений лун Сатурна показал, что скорость света – конечна …

потому что видимое затмение лун
Сатурна происходит с задержкой по времени в зависимости от положения Земли на орбите вокруг Солнца

… метод Кеплера сильно увеличился в точности благодаря часам и телескопу