экзамена
по МАТЕМАТИКЕ
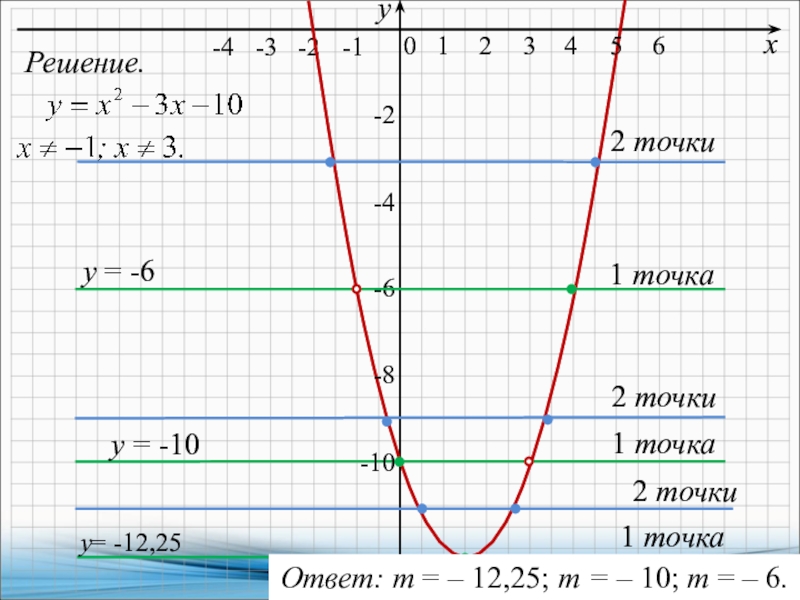
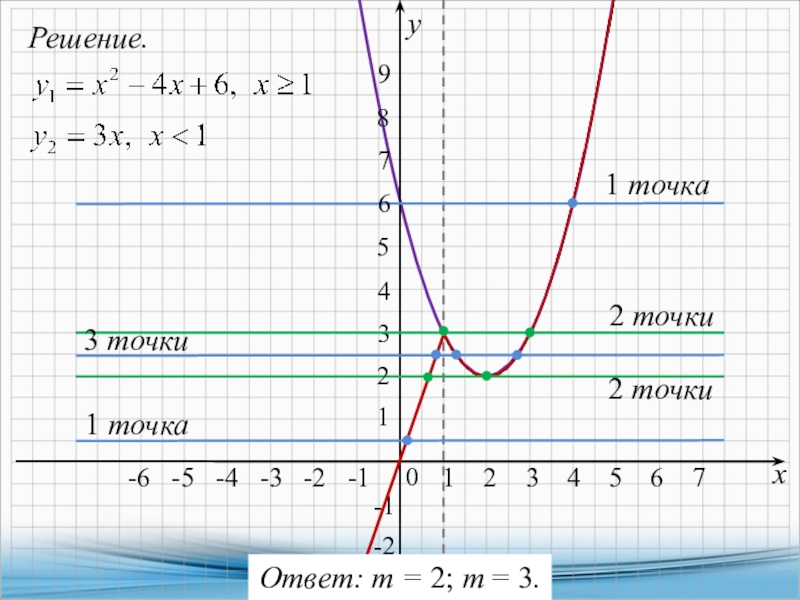
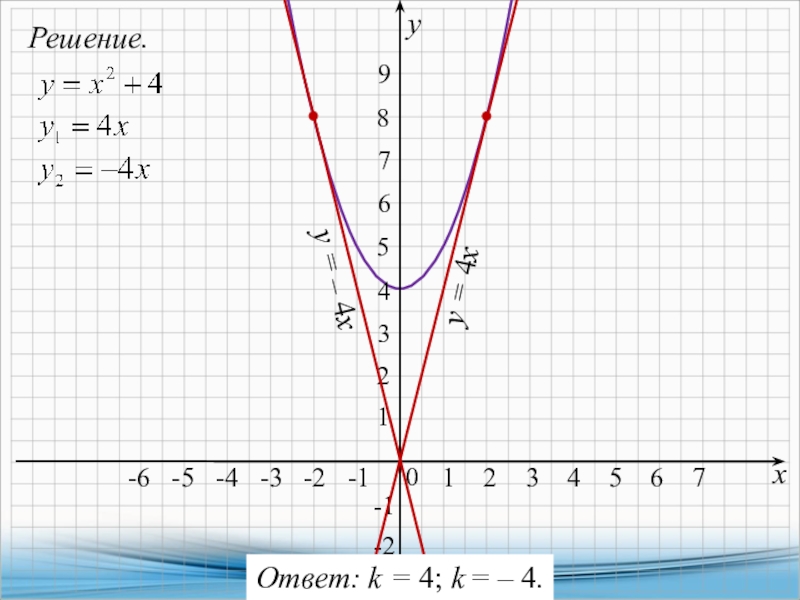
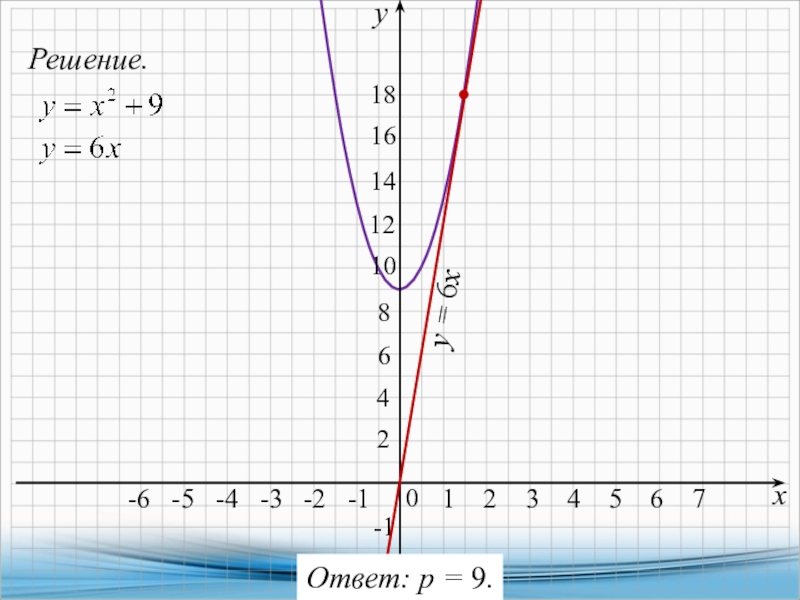
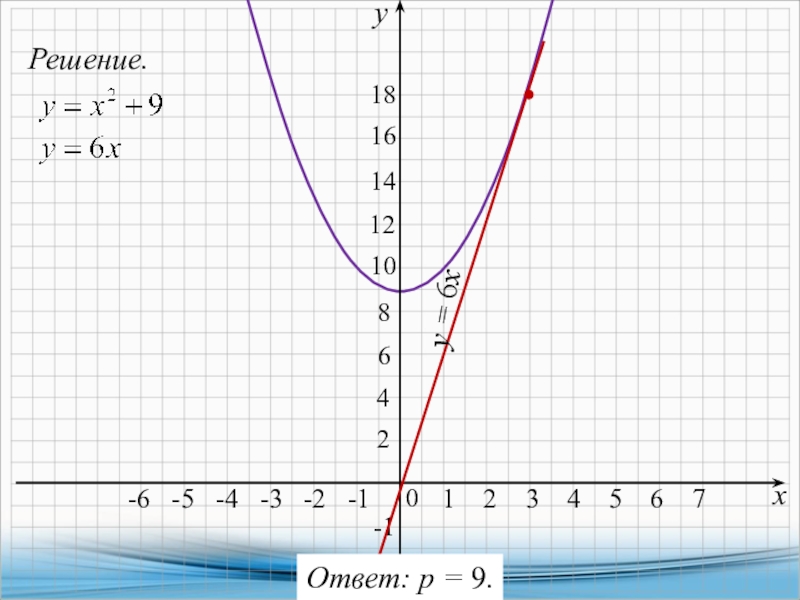
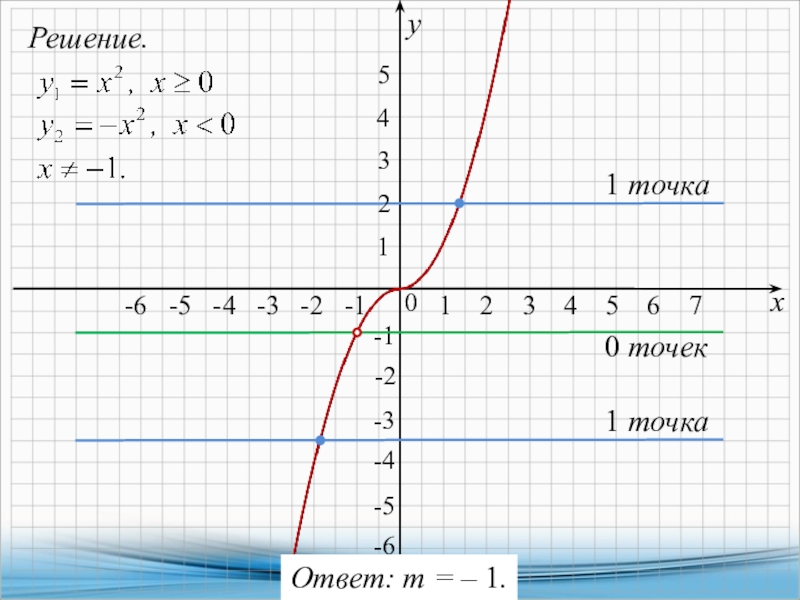
Решение:
Преобразуем функцию, приведем ее к какому-нибудь знакомому виду уравнения
линии. Выпишем числитель, решим биквадратное уравнение, разложим числитель на множители.
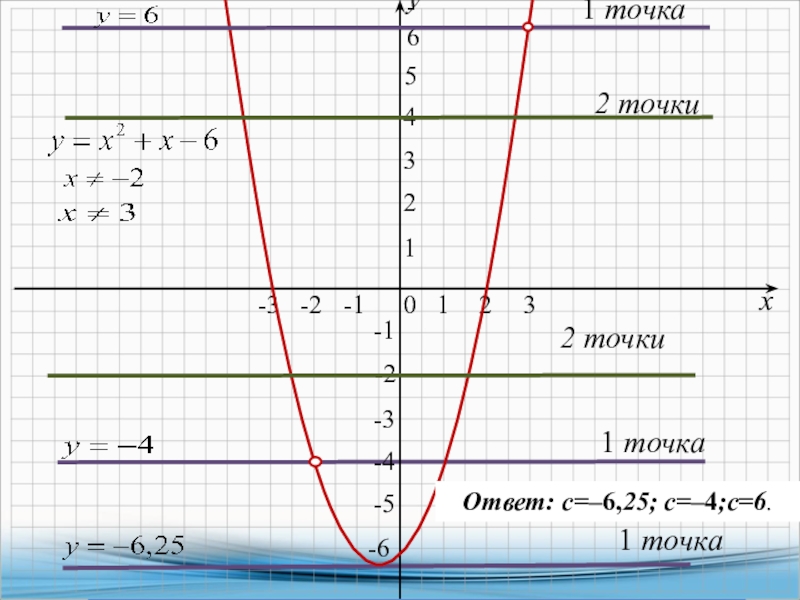
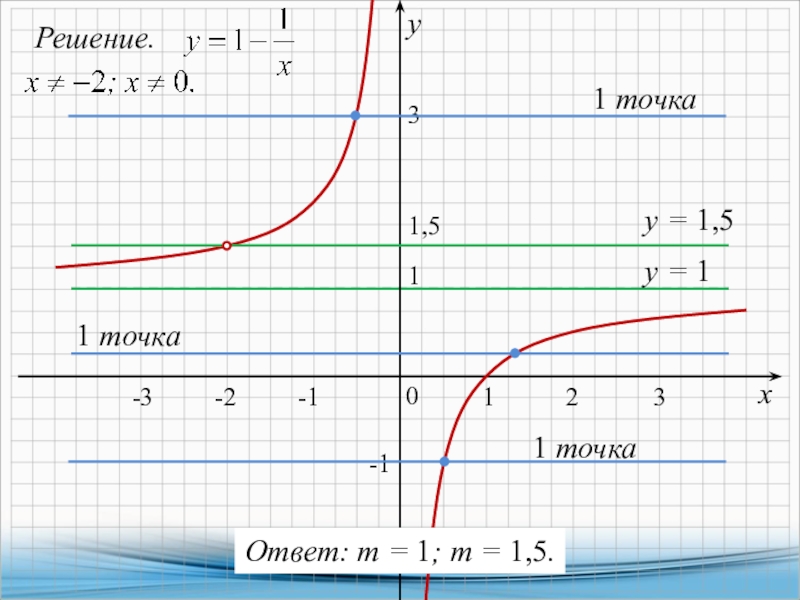
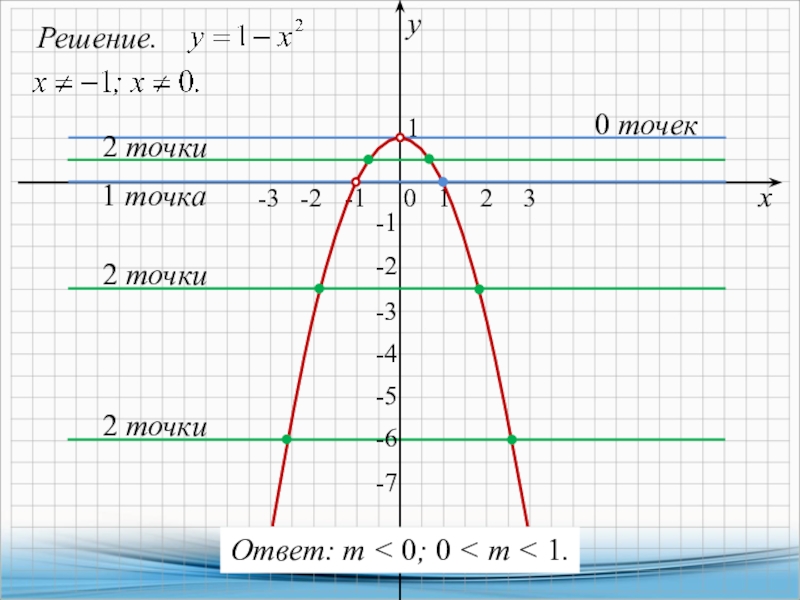
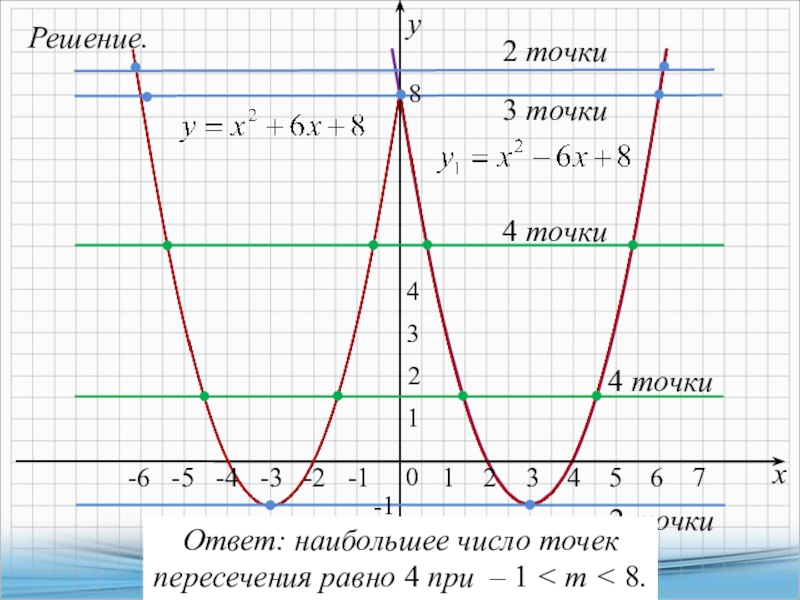
x4-13x2+36=(x2-4)(x2-9)=(x-2)(x+2)(x-3)(x+3).
Тогда,