Глава I. Элементы линейной алгебры § 1. Матрицы и действия над ними

над ними
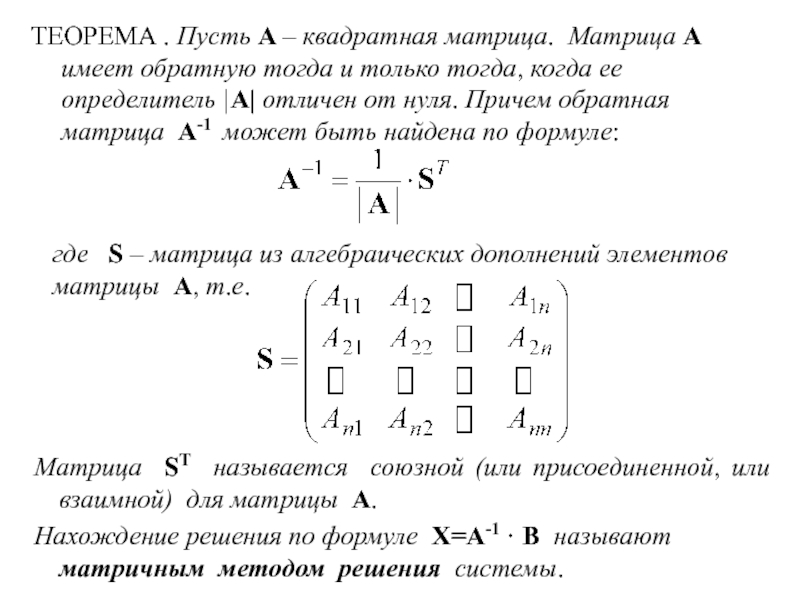
ОПРЕДЕЛЕНИЕ. Матрицей размера mn называется таблица, образованная из элементов

некоторого множества (например, чисел или функций) и имеющая m строк и n столбцов.
Если m  n, то матрицу называют прямоугольной.
Если m  n, то матрицу называют квадратной, порядка n.
Элементы, из которых составлена матрица, называются элементами матрицы.
Например, a24 –
a13 –

Сложение матриц.

столбцов в матрице A должно совпадать с количеством строк матрицы

B);
2) Транспонирование матрицы.
ОПРЕДЕЛЕНИЕ. Пусть A – матрица размера m  n. Матрица размера n  m, полученная из A заменой каждой ее строки столбцом с тем же номером, называется транспонированной к A и обозначается AТ.

матрицы A обозначают |A| , detA или

элементов побочной диагонали.
Определитель третьего порядка равен алгебраической сумме шести произведений.

Со знаком «плюс» берутся произведение элементов главной диагонали и произведения элементов, стоящих в вершинах двух равнобедренных треугольников, основания которых параллельны главной диагонали. Со знаком «минус» берутся произведение элементов побочной диагонали и произведения элементов, стоящих в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали. Т.е.

меняется.
2) При перестановке любых двух строк (столбцов) определитель меняет знак.

3) Общий множитель элементов любой строки (столбца) можно выносить за знак определителя.
4) Определитель равен нулю если:
а) он имеет строку (столбец), состоящую из нулей;
б) он имеет хотя бы две одинаковые строки (столбца);
в) он имеет хотя бы две пропорциональные (т.е. отличающиеся множителем) строки (столбца);
г) хотя бы одна строка (столбец) является линейной комбинацией нескольких других строк (столбцов).

если оно содержит неизвестные только в первой степени и не

содержит произведений неизвестных, т.е. если оно имеет вид a1x1 + a2x2 + … + anxn = b , где ai, b – числа.
ai называются коэффициентами уравнения, b называется свободным членом.
Если b = 0, то уравнение называется однородным. В противном случае уравнение называется неоднородным.
Рассмотрим систему m линейных уравнений с n неизвестными, т.е. систему вида

называют основной матрицей системы (1), матрицу  A* – расширенной матрицей

системы (1).
Пусть X – матрица-столбец неизвестных, B – матрица-столбец свободных членов, т.е.

Тогда систему (1) можно записать в виде матричного уравнения AX=B. Его называют матричной формой системы (1).

матрице A называется матрица, обозначаемая A-1, такая, что A·A-1=A-1

· A=E.

обратную тогда и только тогда, когда ее определитель |A| отличен

от нуля. Причем обратная матрица A-1 может быть найдена по формуле:

где S – матрица из алгебраических дополнений элементов матрицы A, т.е.

Матрица ST называется союзной (или присоединенной, или взаимной) для матрицы A.
Нахождение решения по формуле X=A-1 · B называют матричным методом решения системы.

уравнений m и число неизвестных n совпадает и |A|0, то

система совместна и имеет единственное решение, которое может быть найдено по формулам

где D=|A|, а Di– определитель, получаемый из определителя D заменой его i-го столбца на столбец свободных членов.
Формулы (1) называются формулами Крамера.