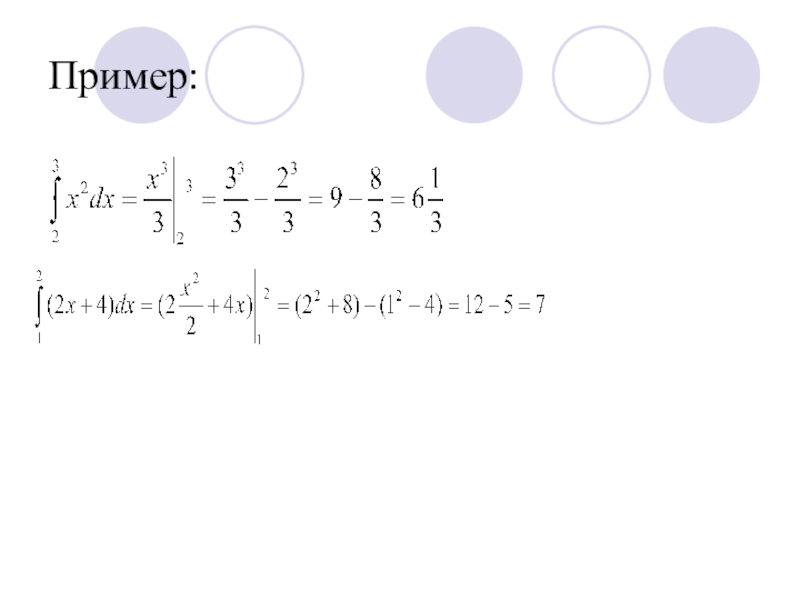Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ИНТЕГРАЛ. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА
Содержание
- 1. ИНТЕГРАЛ. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА
- 2. 1.Внимательно еще раз изучить теорию2.Рассмореть примеры решения 3. Решить самостоятельно
- 3. Слайд 3
- 4. Вопросы для повторения. Что называют криволинейной 1трапецией?2.
- 5. Рассмотрим другой подход к вычислению площади криволинейной
- 6. Слайд 6
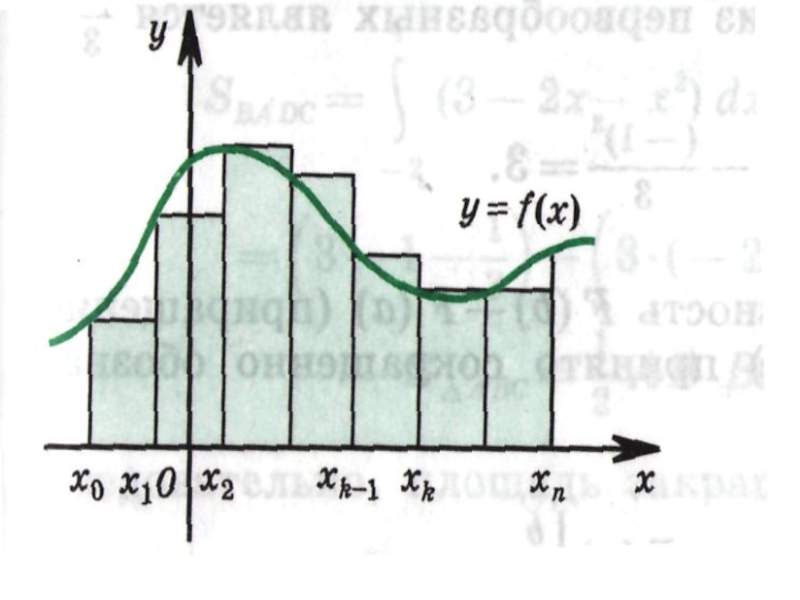
- 7. Разобьём отрезок [а; в] на n отрезков одинаковой длины точками
- 8. При n → ∞ Sn→
- 9. Числа а и в -
- 10. Итак, если f( х )
- 11. Сравнивая формулы криволинейных трапеций :
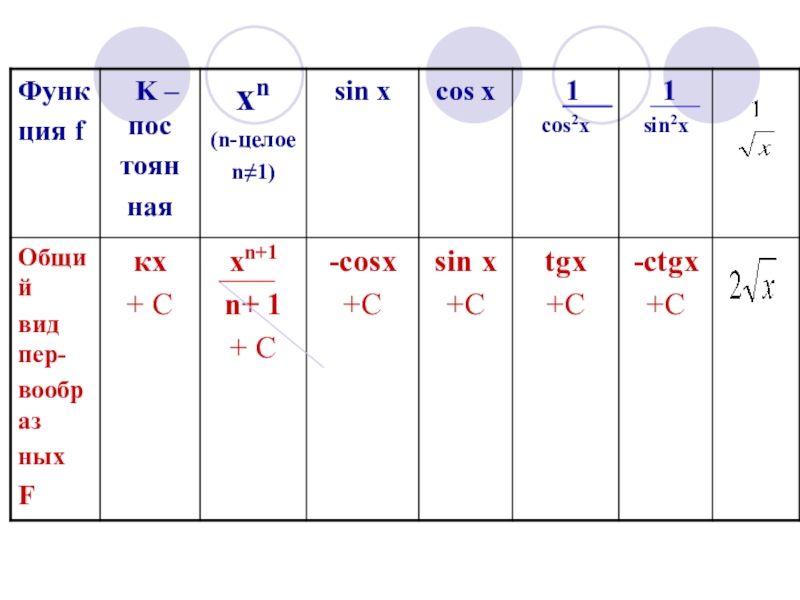
- 12. Формула Ньютона-Лейбница
- 13. Иссак Ньютон(1643-1716)ГотфридЛейбниц(1646-1716).
- 14. Слайд 14
- 15. Слайд 15
- 16. Пример:
- 17. Выполнить самостоятельно
- 18. Скачать презентанцию
1.Внимательно еще раз изучить теорию2.Рассмореть примеры решения 3. Решить самостоятельно
Слайды и текст этой презентации
Слайд 4Вопросы для повторения
. Что называют криволинейной 1трапецией?
2. Являются ли фигуры,
изображённые на графиках криволинейными трапециями?
криволинейной трапеции
Слайд 5Рассмотрим другой подход к вычислению площади криволинейной трапеции
Будем считать функцию
f неотрицательной и непрерывной на отрезке [а; в], тогда площадь
S соответствующей криволинейной трапеции можно приближённо подсчитать следующим образом
![Разобьём отрезок [а; в] на n отрезков одинаковой длины точками](/img/tmb/6/595559/b36d97d50bbe9ab081faf588f0513e0d-800x.jpg "ИНТЕГРАЛ. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА Разобьём отрезок [а; в] на n отрезков одинаковой длины точками")
Слайд 8 При n → ∞
Sn→ к некоторому числу
Это число
называют интегралом функции f от а до в и обозначают:
в∫ f(х)dх
а
Слайд 9 Числа а и в - называются пределами
интегрирования, а – нижним пределом, в – верхним.
Знак
∫ - называют знаком интегралаФункцию f называют подынтегральной функцией, а переменная х – переменной интегрирования
df- знак дифференциала
Слайд 10 Итак, если f( х ) ≥0 на отрезке
[а; в], то
Площадь соответствующей криволинейной трапеции выражается формулой:
вS = ∫ f(х)dх
а
![Итак, если f( х ) ≥0 на отрезке [а; в], то Площадь соответствующей криволинейной трапеции](/img/tmb/6/595559/859a74a96bc2ac71970a44ddb7fb7c5f-800x.jpg "ИНТЕГРАЛ. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА Итак, если f( х ) ≥0 на отрезке [а; в],")
