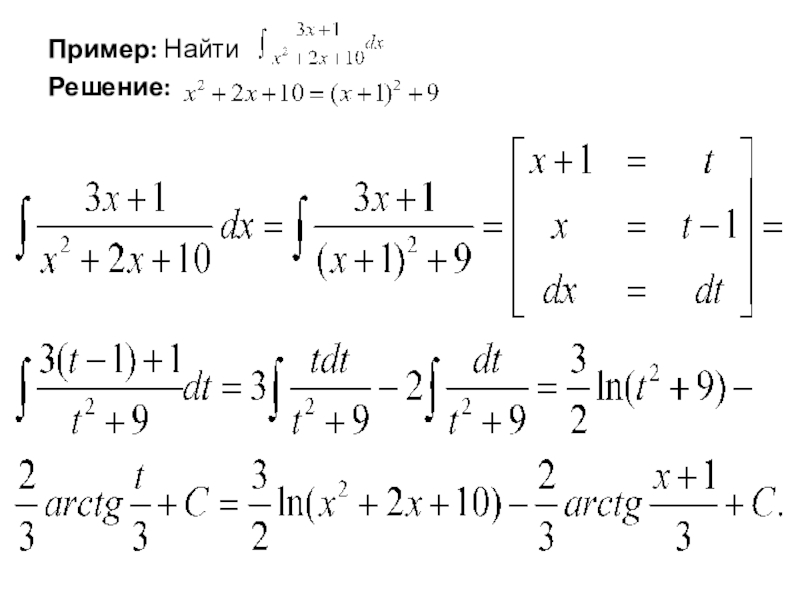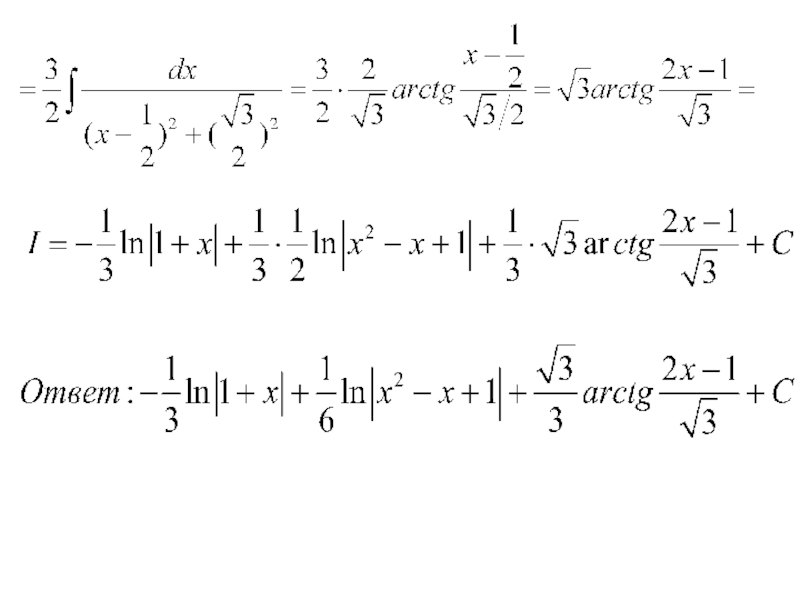Слайд 1Интегрирование дробно-рациональных функций
Дробно-рациональной функцией (или рациональной
дробью)называется функция,равная отношению двух многочленов,т.е.
,где - многочлен
степени m,а -многочлен степени n.
Рациональная дробь называется правильной,если степеньчислителя меньше степени знаменателя,т.е.
в противном случае (если )рациональная дробь называется неправильной.
Слайд 2Всякую неправильную рациональную дробь
можно,путем деления числителя на знаменатель представить
в виде суммы многочлена и правильной рациональной дроби т.е.
Например
Делим числитель на знаменатель в столбик.
Получим частное и остаток .
Следовательно
Слайд 3Правильные рациональные дроби вида:
1)
2)
(корни
комплексные,т.е. )
(k >2,корни знаменателя комплексные),
Где А,а,М,N,р,q-действительные числа,называются простейшими рациональными дробями 1,2,3 и 4 типов.
Слайд 4Теорема: Всякую правильную рациональную дробь
Знаменатель которой разложен на множители
можно представить
(и притом единственным образом ) в виде следующей суммы простейших
дробей:
(*)
где некоторые действительные коэффициенты.
Слайд 5Поясним формулировку теоремы на следующих примерах:
1)
2)
3)
Для нахождения неопределённых коэффициентов
Можно
применить метод сравнивания коэффициентов.
Суть метода такова:
Слайд 6В правой части равенства(*)приведем к общему знаменателю
;в результате получим тождество
гдеS(x)-многочлен с
неопределёнными коэффициентами.
2)Так как в полученном тождестве знаменатели равны ,то тождественно равны и числители, т.е.
3)Приравнивая коэффициенты при одинаковых степенях
в обеих частях тождества, получим систему линейных уравнений ,из которой и определим искомые коэффициенты
Слайд 7Пример: Представить дробь
В виде суммы
простейших дробей.
Решение: Согласно теореме имеем:
Отсюда следует
Приравнивая коэффициенты при
получаем
Слайд 8Решаем систему, находим, что
Для нахождения неопределённых коэффициентов применяют также метод
отдельных значений аргумента
после получения тождества(**) аргументу х придают
конкретные значения столько раз, сколько неопределённых коэффициентов(обычно полагают вместо х значения действительных корней многочлена
Слайд 9Найдём интегралы от простейших рациональных дробей.
1)
(формула (2) таблицы интегралов)
2)
(формула (1))
Выделяем в знаменателе полный .
квадрат, делаем замену и подстановку в числителе.
Слайд 11Интегрирование рациональных дробей
Сформулируем общее правило интегрирования рациональных дробей:
1).Если
дробь неправильная, то представить её в виде суммы многочлена и
правильной дроби;
2)Разложив знаменатель правильной рациональной дроби на множители , представить её в виде суммы простейших рациональных дробей;
3)Проинтегрировать многочлен и полученную сумму простейших дробей.
Слайд 12
Пример:Найти интеграл
Решение: Под знаком интеграла неправильная дробь; выделим её целую
часть путём деления числителя на знаменатель. Получаем:
Разложим правильную рациональную дробь
на простейшие дроби:
Слайд 13Отсюда следует,что
Находим :
Таким образом получаем ,что:
Найдем искомый интеграл, преобразуя подынтегральную
дробно-рациональную функцию, представляя её в виде полученной суммы.
Слайд 15Следовательно,
Отметим,что любая рациональная функция интегрируется в элементарных функциях.
Слайд 16Пример:Вычислить
Решение: Преобразуем знаменатель дроби
Выделим целую часть в дроби (поделим многочлен,
стоящий в числителе на многочлен знаменателя)
Поэтому
Дробь
Слайд 17Умножая обе части равенства на(х-3)(х-4),получаем
Решая систему с двумя неизвестными находим
значения
А=-32;В=70.
Дробь
А
Слайд 18Пример: Вычислить
Решение: Так как
А корни трёхчлена комплексны, то дробь запишем
в виде
Слайд 19
Откуда вычитая из(2)-(3) получим:
Таким образом имеем:
Тогда:
Слайд 20Решим отдельно второй интеграл т.к. первый табличный №2:
Пусть
1)
2)