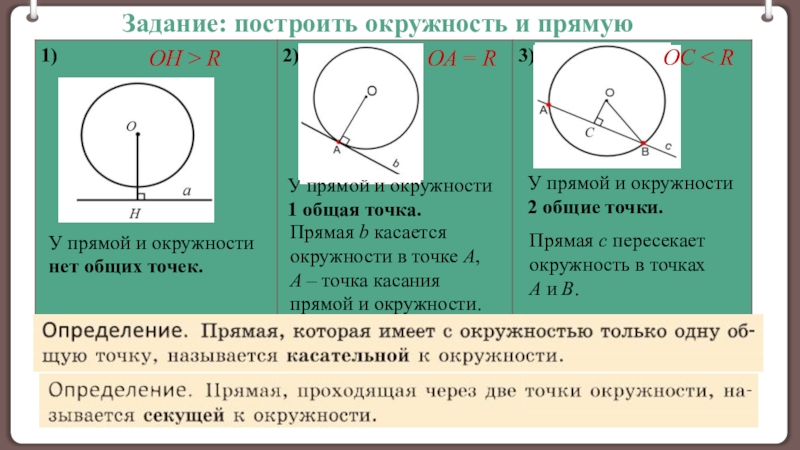
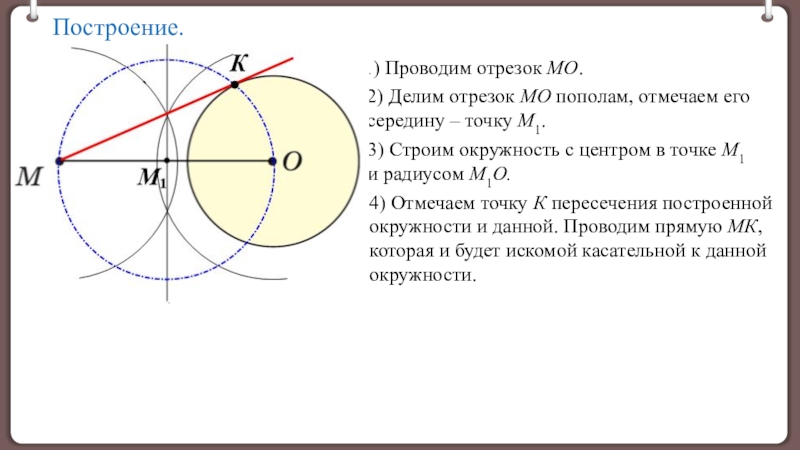
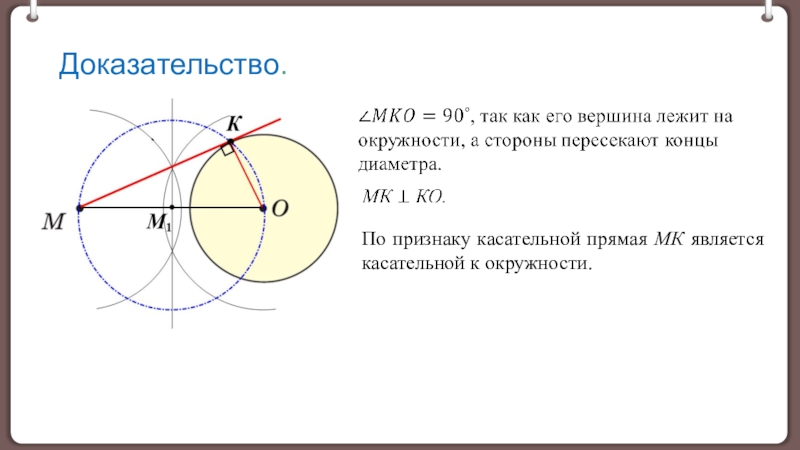
окружности.
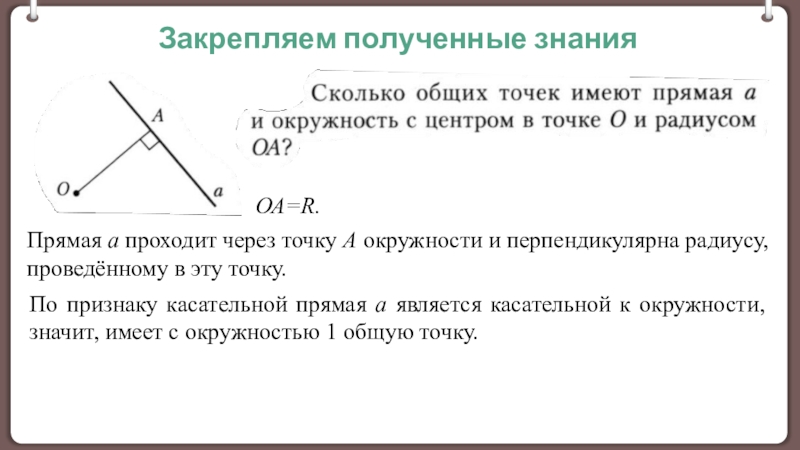
Признак касательной к окружности.
Свойство касательной.
Свойство касательных, проведённых из одной точки
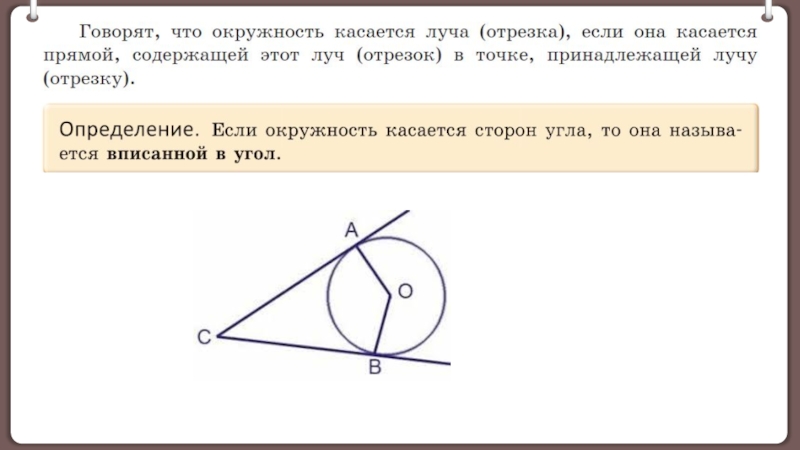
к окружности.Определение окружности, вписанной в угол.
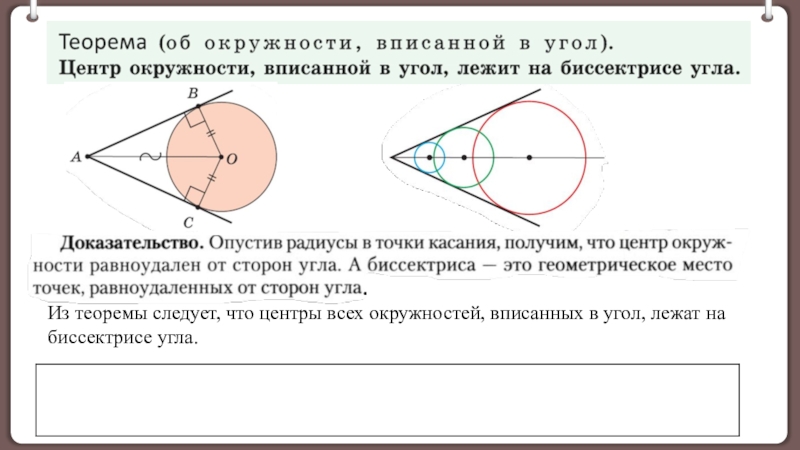
Свойство окружности, вписанной в угол.