Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 21
Содержание
- 1. Лекция 21
- 2. Координатный способИмеет ограниченное применение. Он используется главным
- 3. Задача: Построить перспективу прямой АВ Для построения
- 4. Выбираем начало координат (.)О, положение наблюдателя (проекцию на картину- главную точку Р и дистанцию РS)°°О°РSh
- 5. Основание картины совпадает с осью Х, ось
- 6. Перспективный масштабКоординатные оси, построенные в перспективе, называются
- 7. Построим перспективу вторичной проекции точки А.
- 8. Координату Уа фиксируем на оси У как
- 9. Можно воспользоваться дробной дистанционной точкой. В этом
- 10. Строим в перспективе вторичную проекцию точки В
- 11. Для определения перспективного изображения точек А и
- 12. На полученной глубине Уа и Ув определяем
- 13. Способ перспективной сеткиСпособ является разновидностью координатного способаОн
- 14. Способ перспективной сеткиНа план объекта после выбора
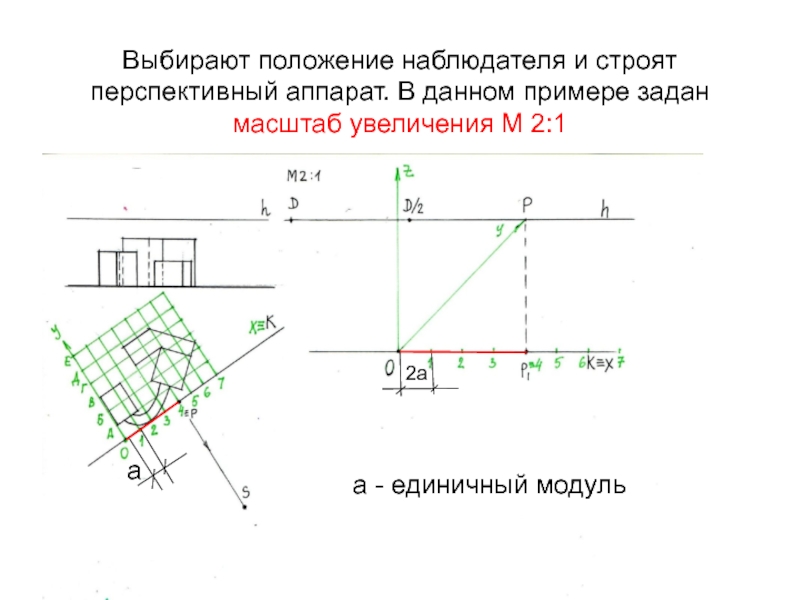
- 15. Выбирают положение наблюдателя и строят перспективный аппарат.
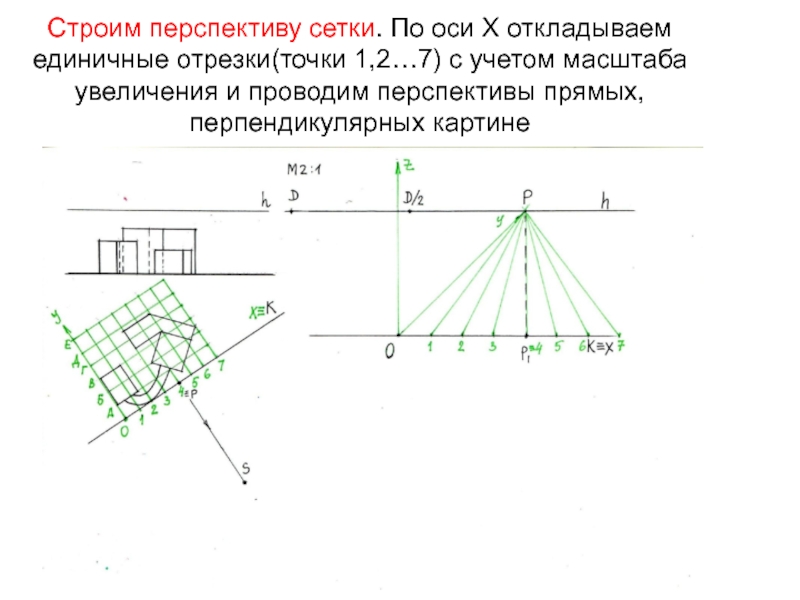
- 16. Строим перспективу сетки. По оси Х откладываем
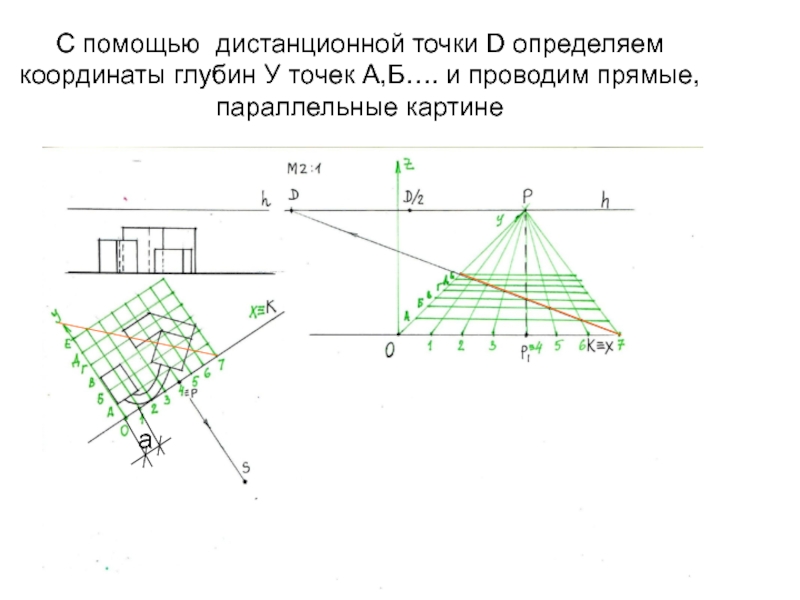
- 17. С помощью дистанционной точки D определяем координаты глубин У точек А,Б…. и проводим прямые, параллельные картинеа
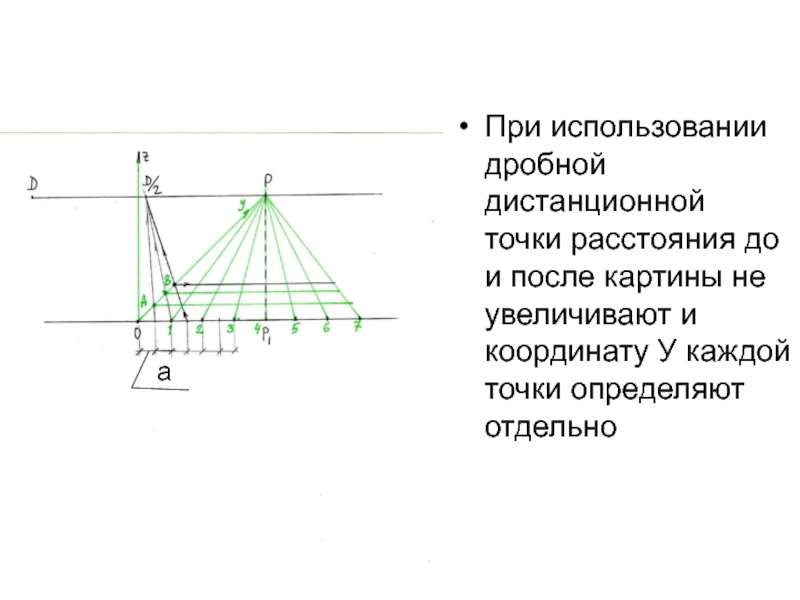
- 18. При использовании дробной дистанционной точки расстояния до
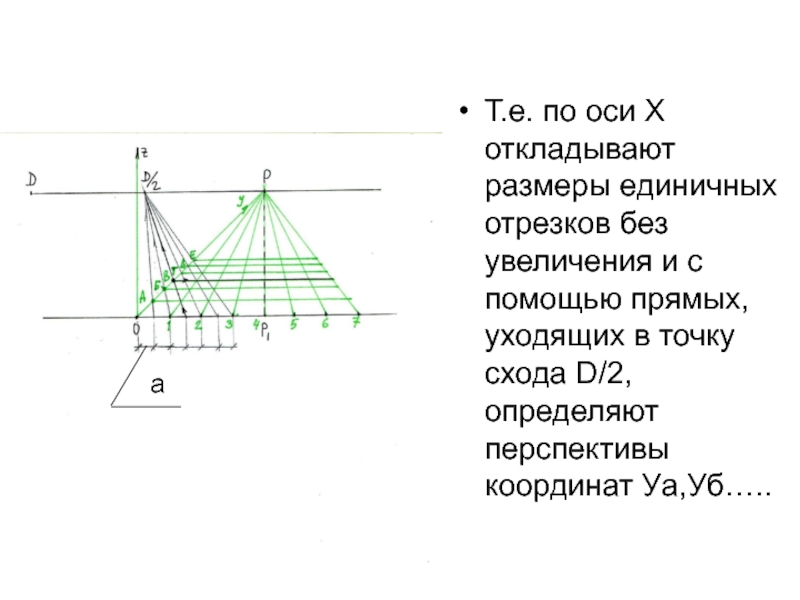
- 19. Т.е. по оси Х откладывают размеры единичных
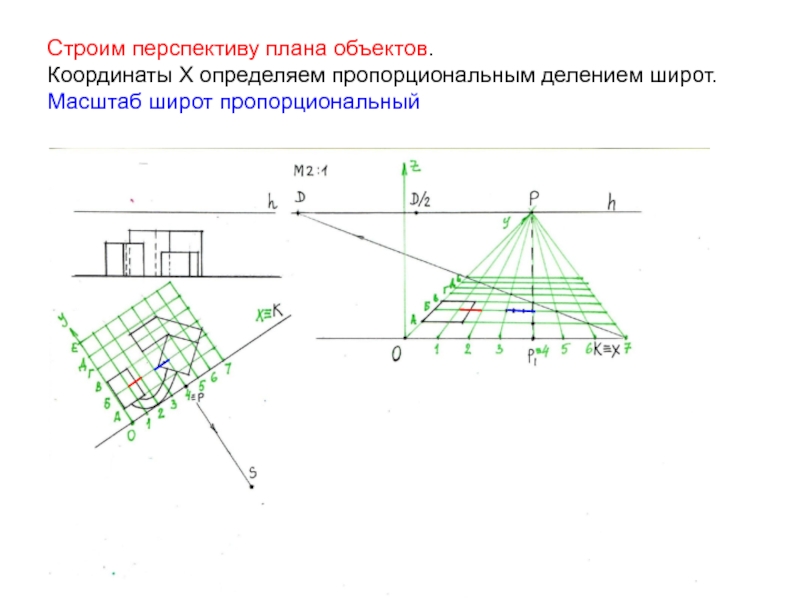
- 20. Строим перспективу плана объектов. Координаты Х определяем пропорциональным делением широт. Масштаб широт пропорциональный
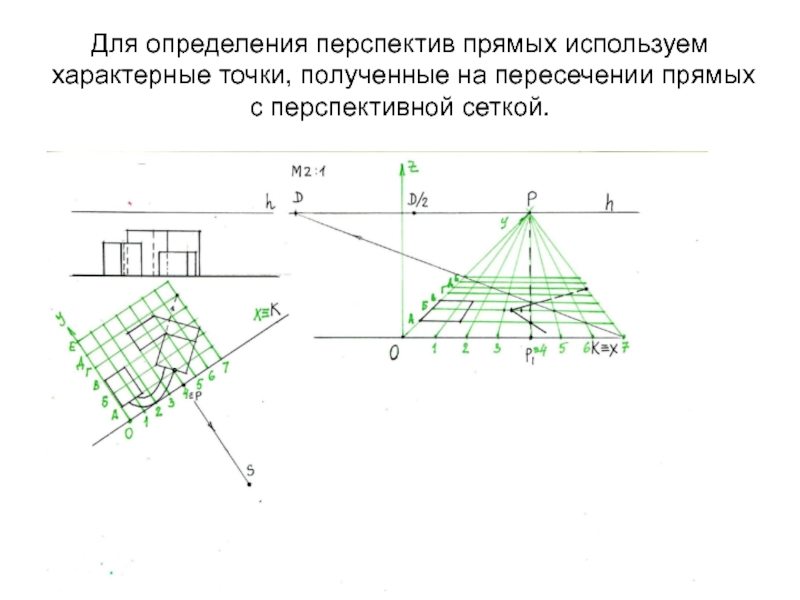
- 21. Для определения перспектив прямых используем характерные точки, полученные на пересечении прямых с перспективной сеткой.°
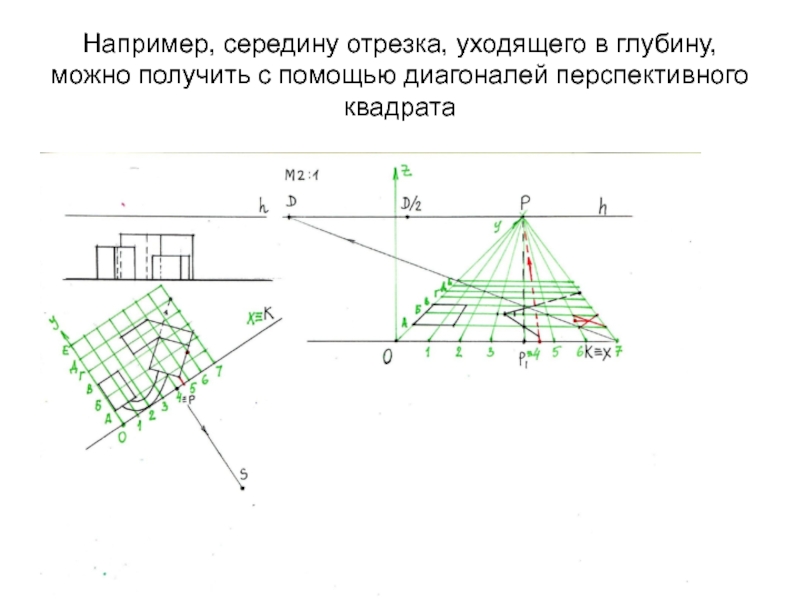
- 22. Например, середину отрезка, уходящего в глубину, можно получить с помощью диагоналей перспективного квадрата
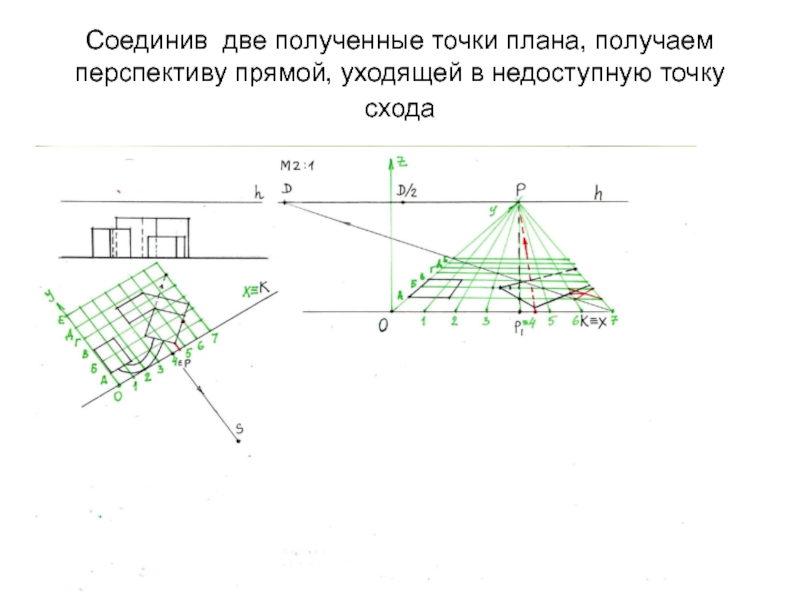
- 23. Cоединив две полученные точки плана, получаем перспективу прямой, уходящей в недоступную точку схода
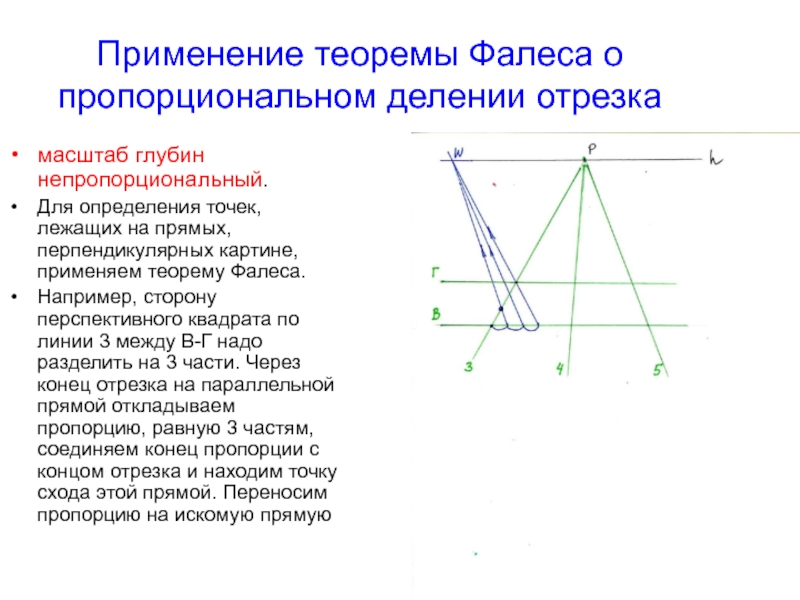
- 24. Применение теоремы Фалеса о пропорциональном делении отрезкамасштаб
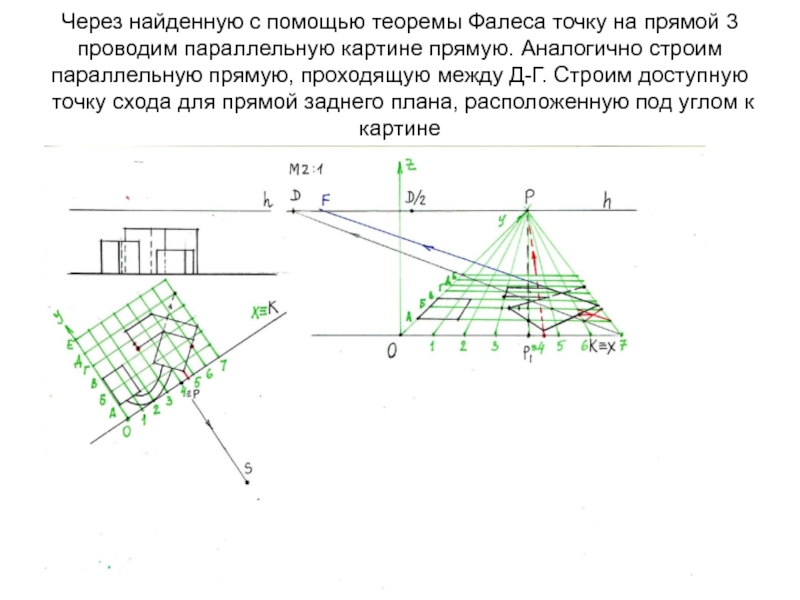
- 25. Через найденную с помощью теоремы Фалеса точку
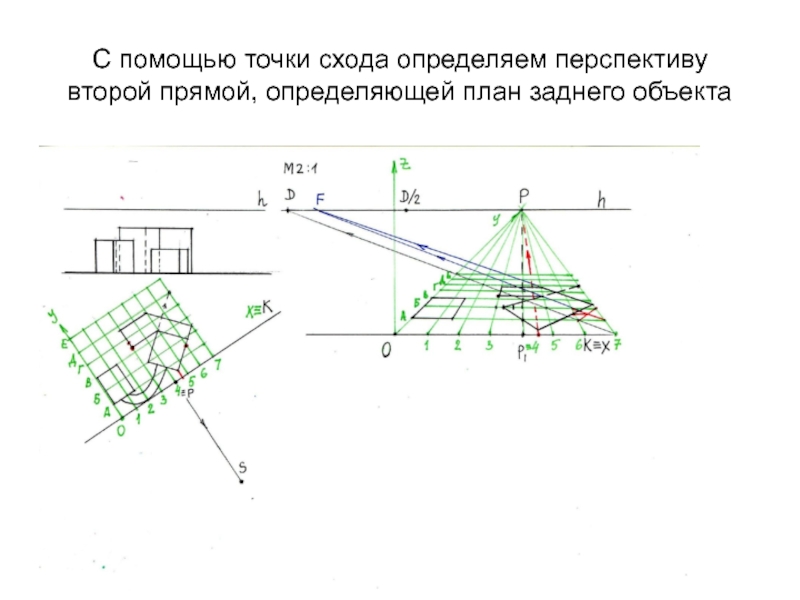
- 26. С помощью точки схода определяем перспективу второй прямой, определяющей план заднего объекта
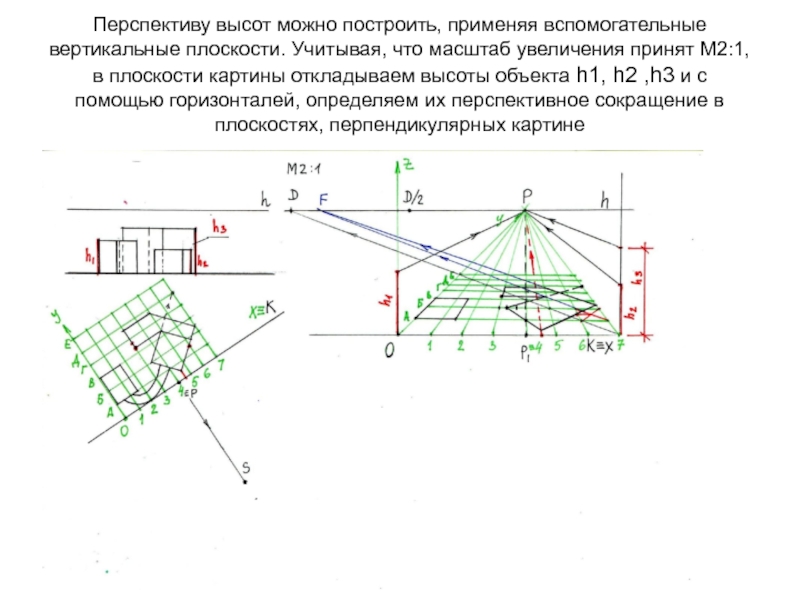
- 27. Перспективу высот можно построить, применяя вспомогательные вертикальные
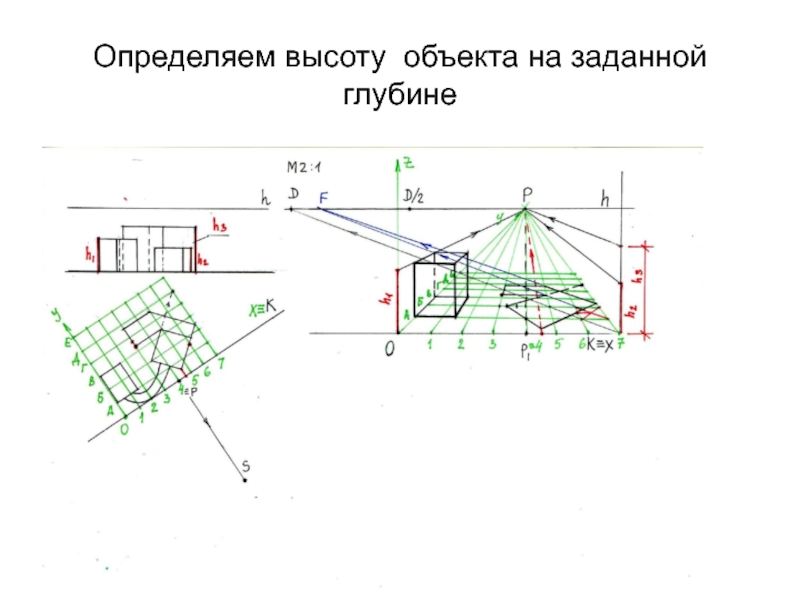
- 28. Определяем высоту объекта на заданной глубине
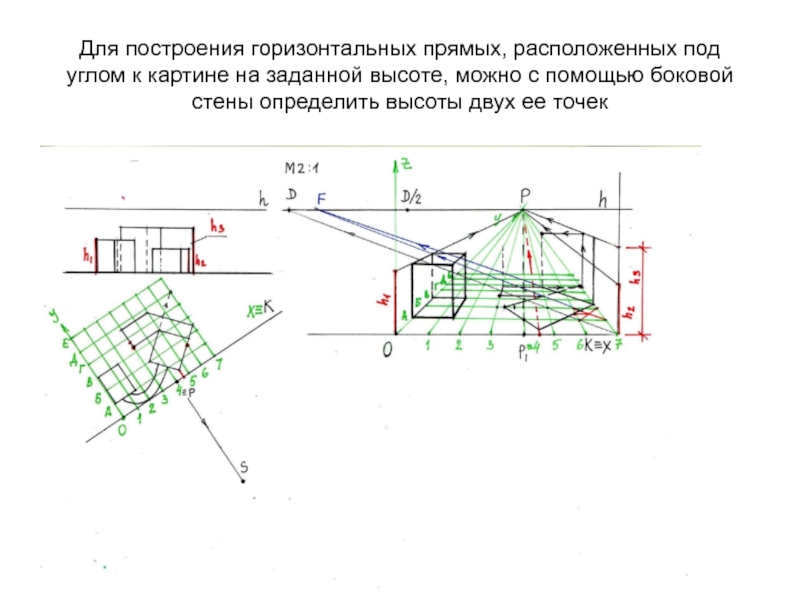
- 29. Для построения горизонтальных прямых, расположенных под углом
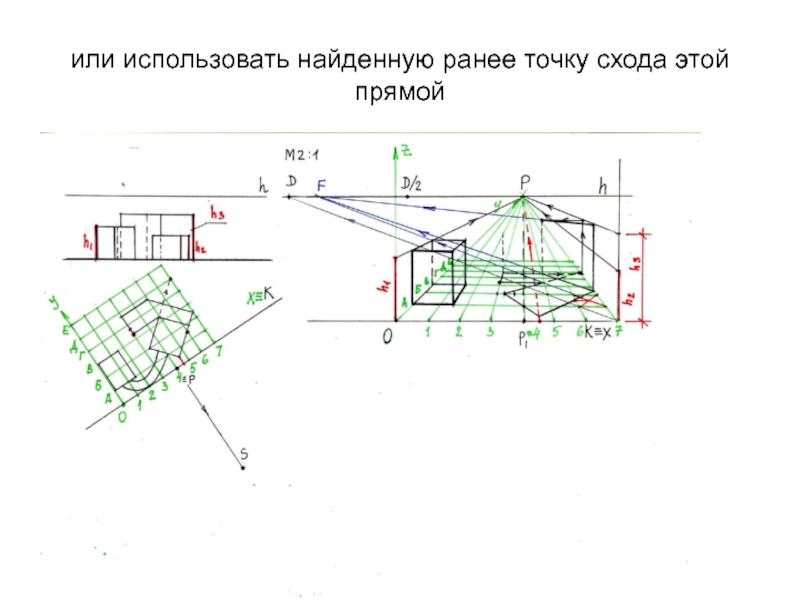
- 30. или использовать найденную ранее точку схода этой прямой
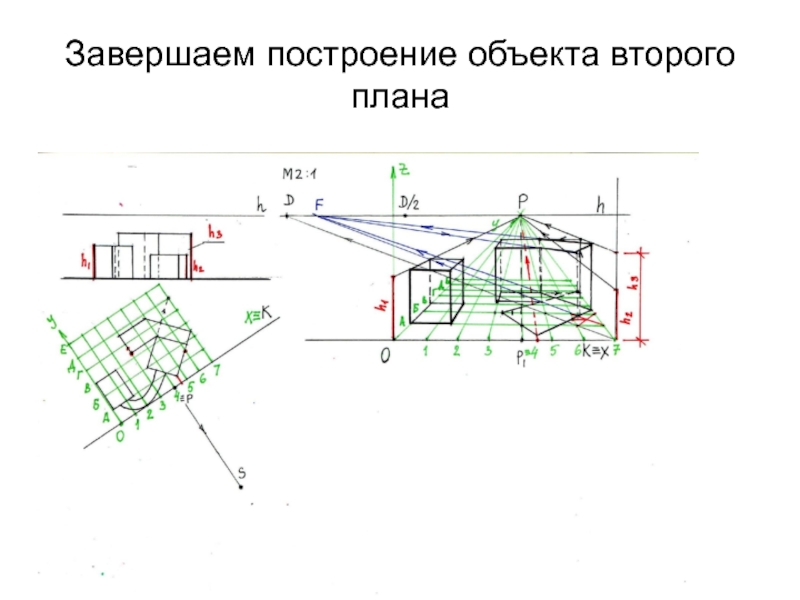
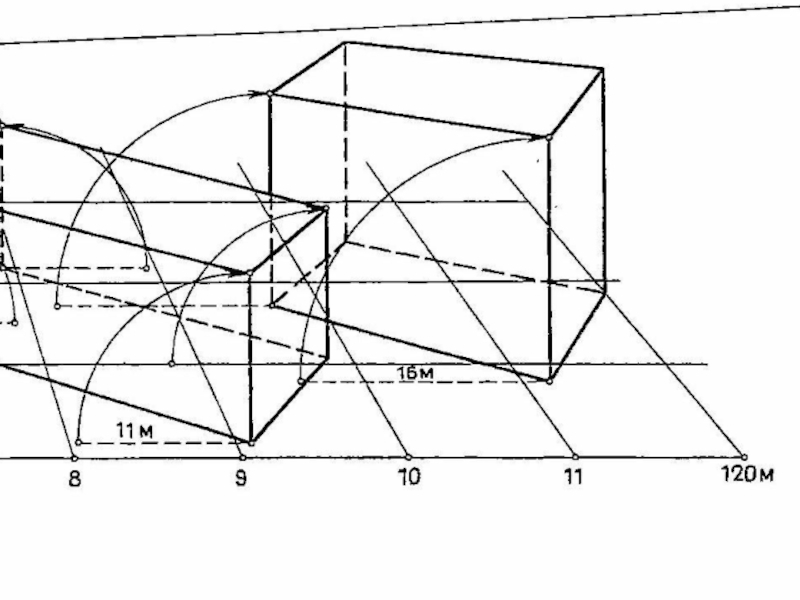
- 31. Завершаем построение объекта второго плана
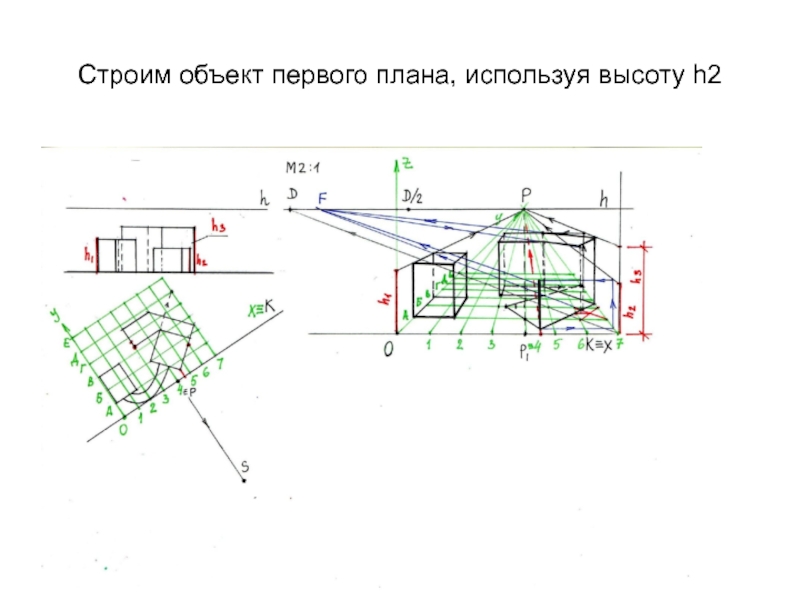
- 32. Строим объект первого плана, используя высоту h2
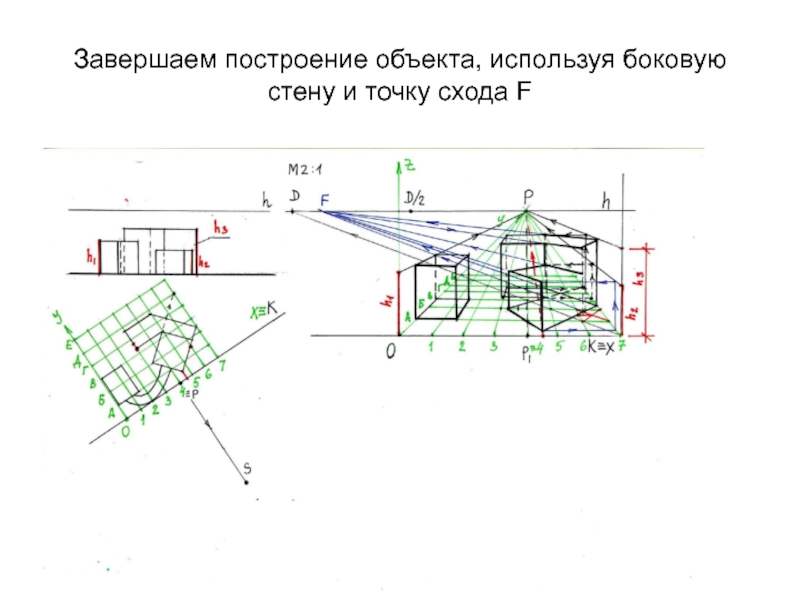
- 33. Завершаем построение объекта, используя боковую стену и точку схода F
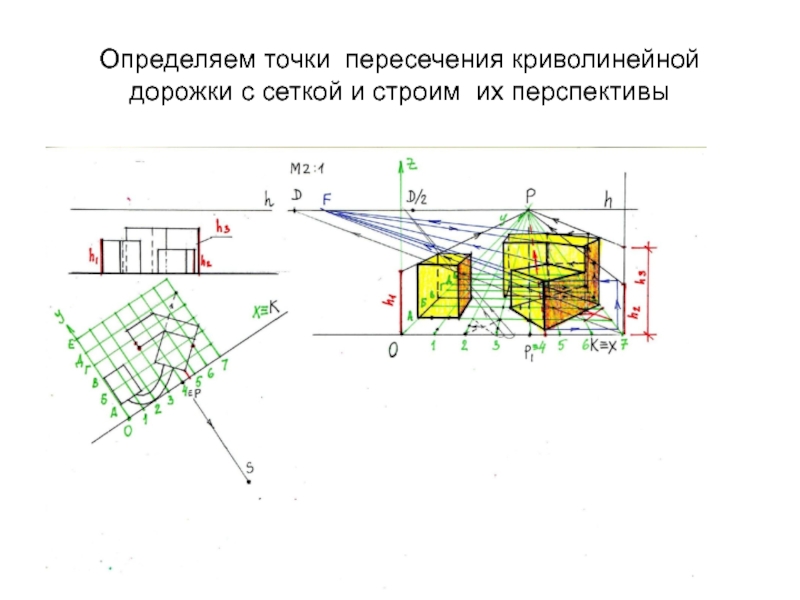
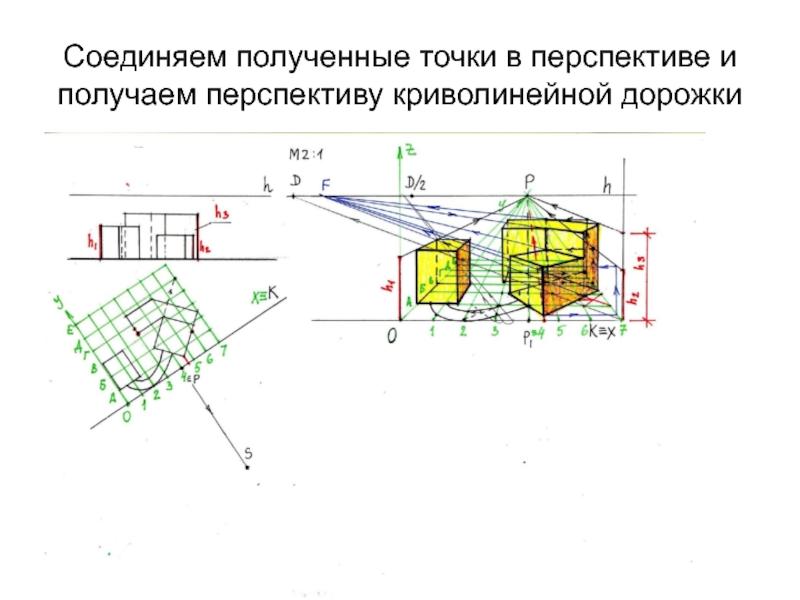
- 34. Определяем точки пересечения криволинейной дорожки с сеткой и строим их перспективы
- 35. Соединяем полученные точки в перспективе и получаем перспективу криволинейной дорожки
- 36. Определение высоты объекта (второй способ)Высоту объекта
- 37. Слайд 37
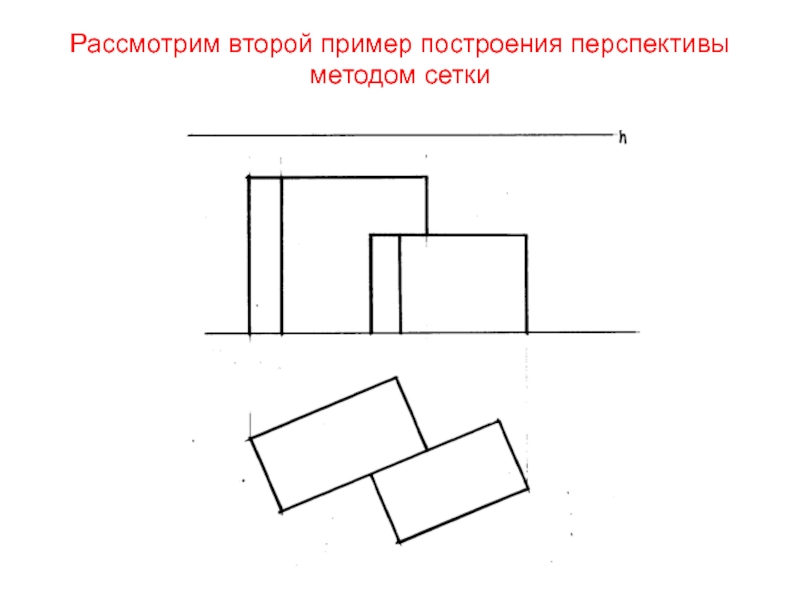
- 38. Рассмотрим второй пример построения перспективы методом сетки
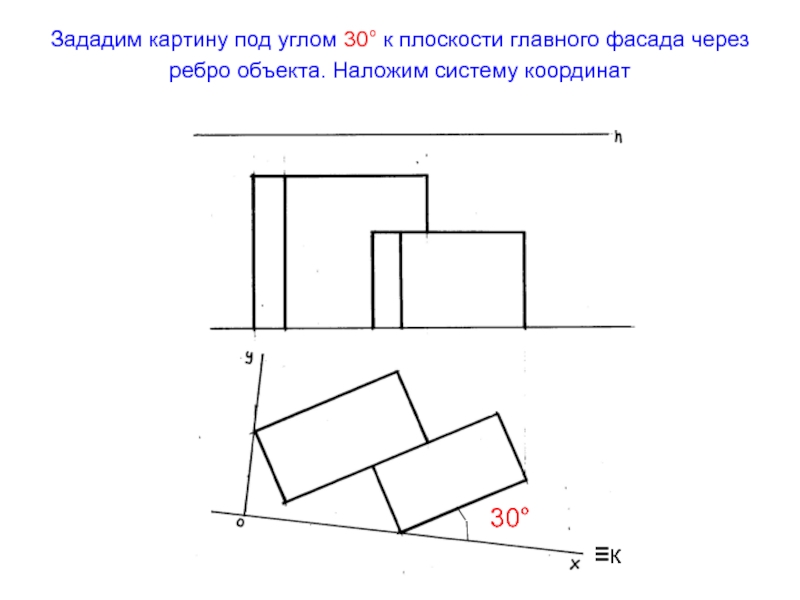
- 39. Зададим картину под углом 30° к плоскости главного фасада через ребро объекта. Наложим систему координат ≡к30°
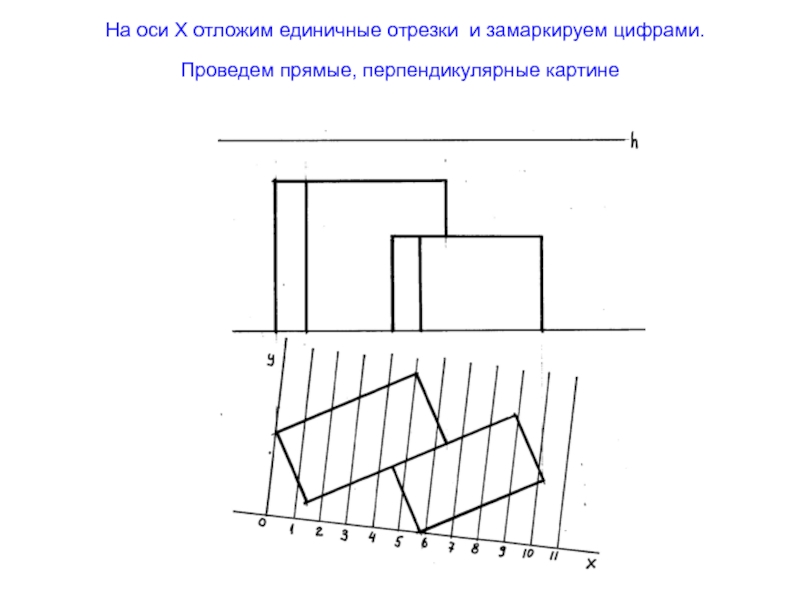
- 40. На оси Х отложим единичные отрезки и замаркируем цифрами. Проведем прямые, перпендикулярные картине
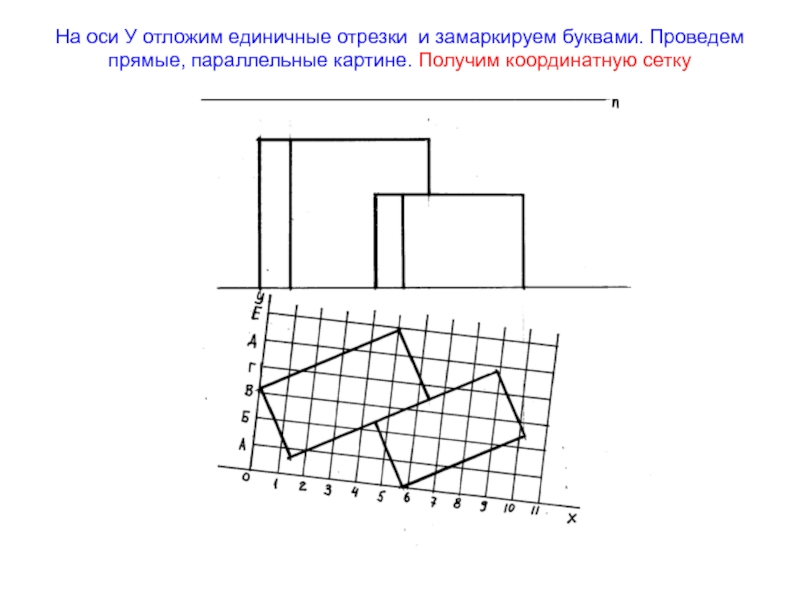
- 41. На оси У отложим единичные отрезки и замаркируем буквами. Проведем прямые, параллельные картине. Получим координатную сетку
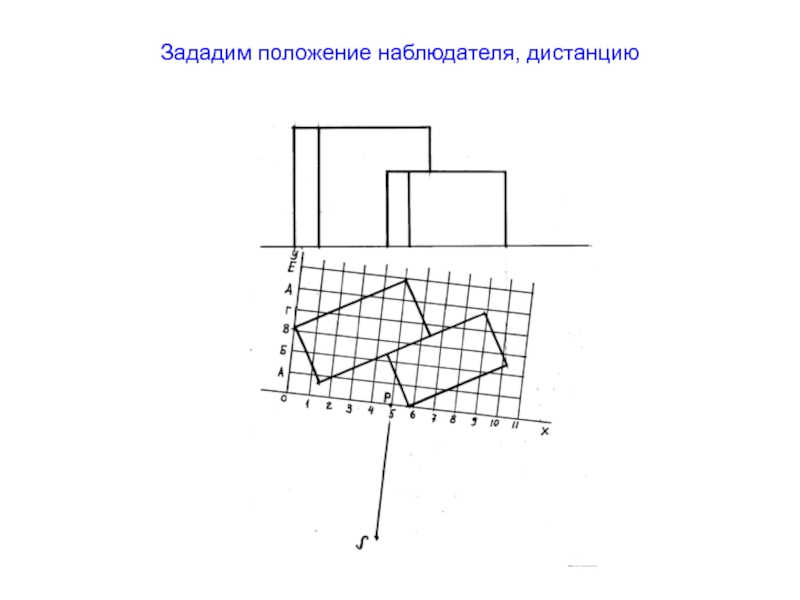
- 42. Зададим положение наблюдателя, дистанцию
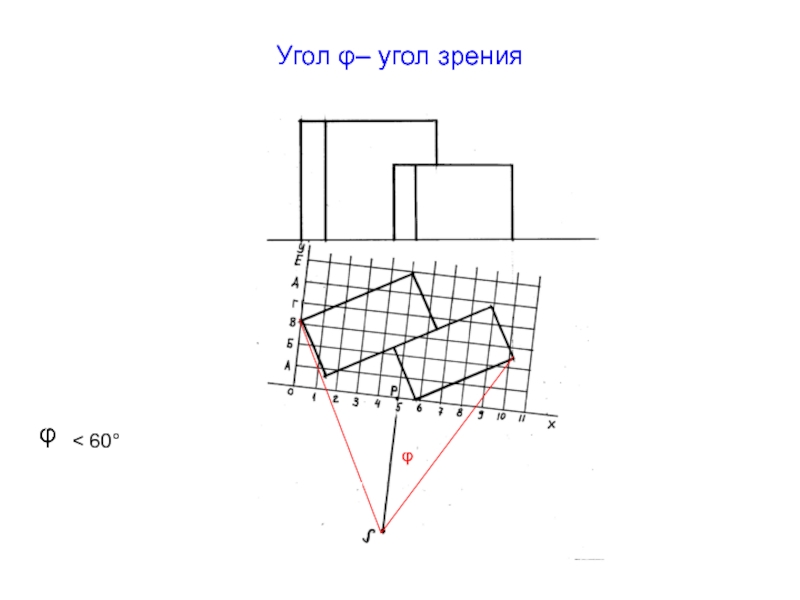
- 43. Угол φ– угол зренияφα < 60°φ
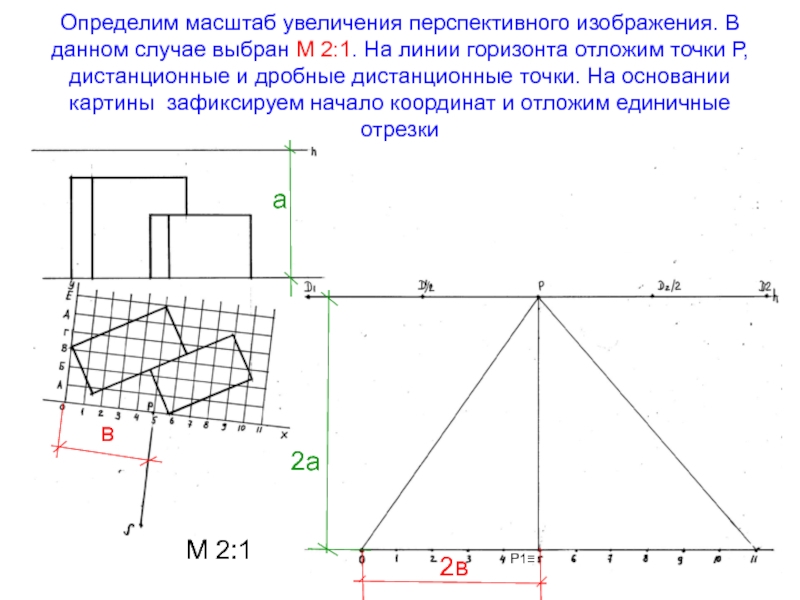
- 44. Определим масштаб увеличения перспективного изображения.
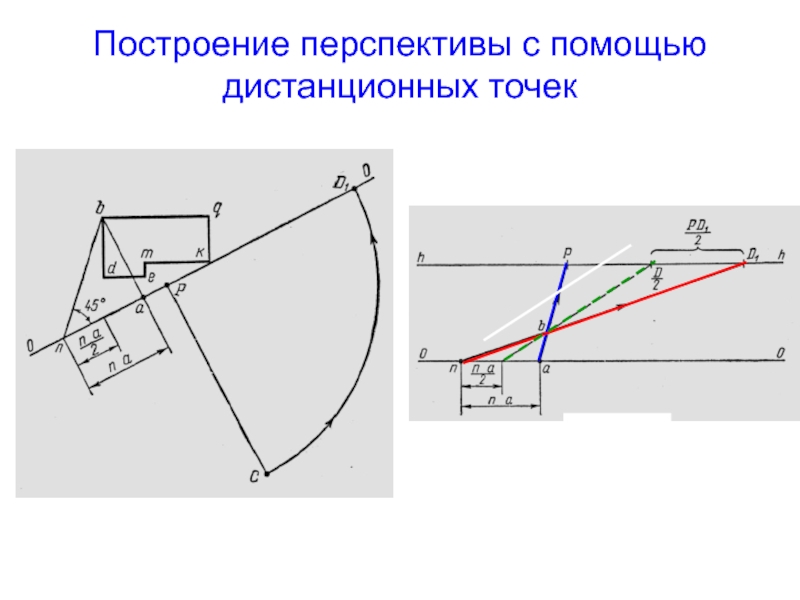
- 45. Построение перспективы с помощью дистанционных точек
- 46. Определим положение точки Е, лежащей на оси
- 47. Зафиксируем на эпюре точки пересечения перспективы прямой,
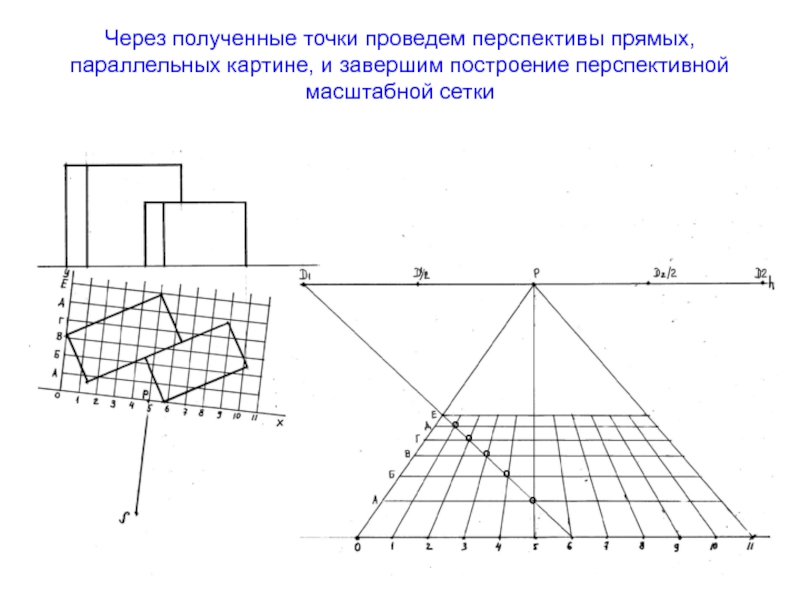
- 48. Через полученные точки проведем перспективы прямых, параллельных картине, и завершим построение перспективной масштабной сетки°°°°°
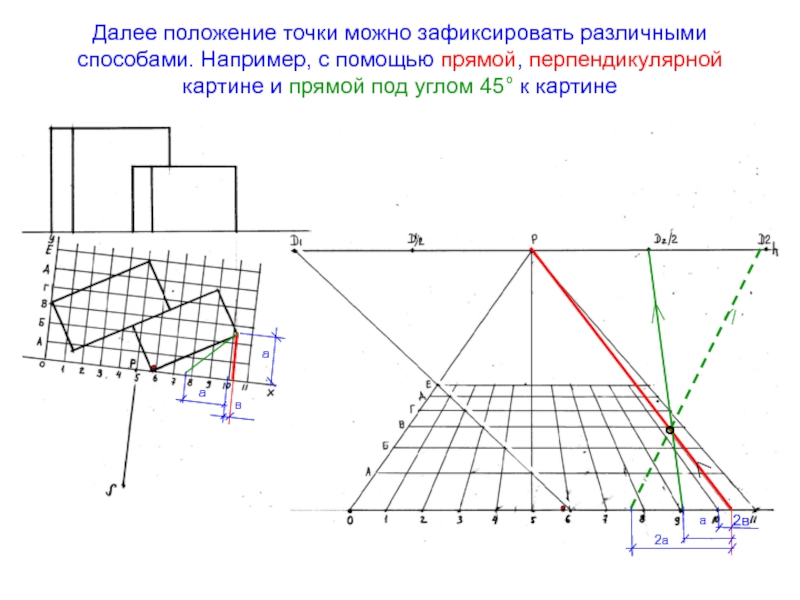
- 49. Далее положение точки можно зафиксировать различными способами.
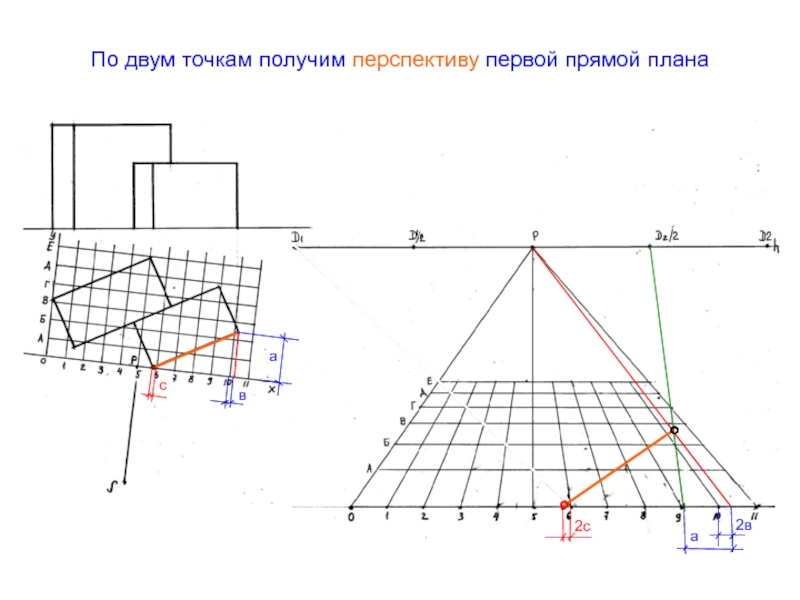
- 50. По двум точкам получим перспективу первой прямой плана°°св2с2ваа
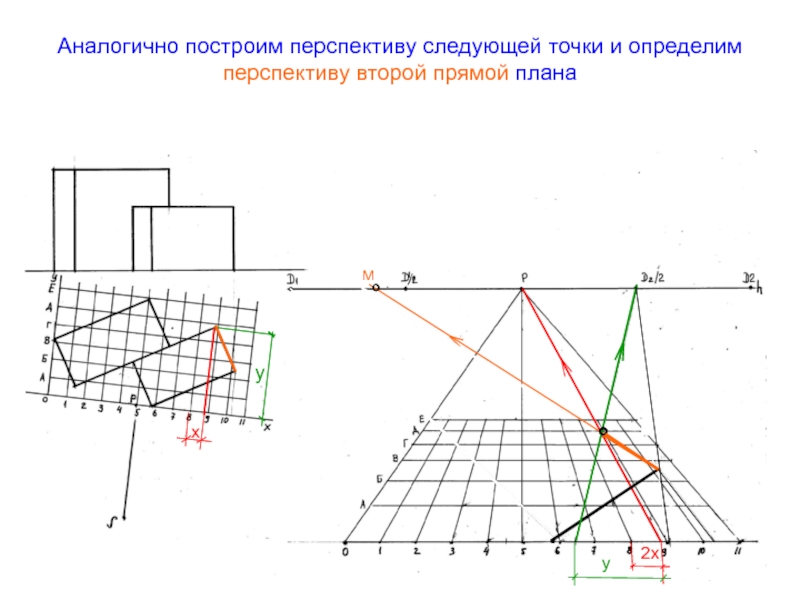
- 51. Аналогично построим перспективу следующей точки и определим перспективу второй прямой планаМух2ху°°
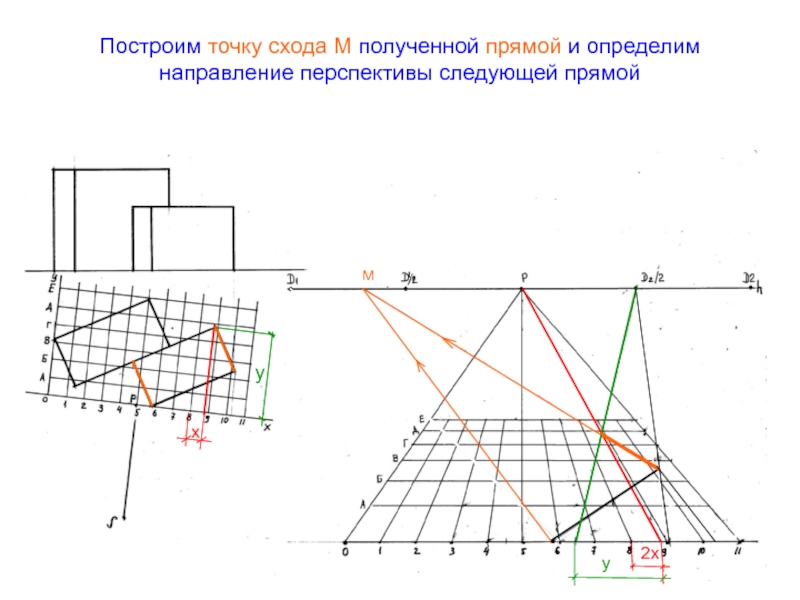
- 52. Построим точку схода М полученной прямой и определим направление перспективы следующей прямойМух2ху
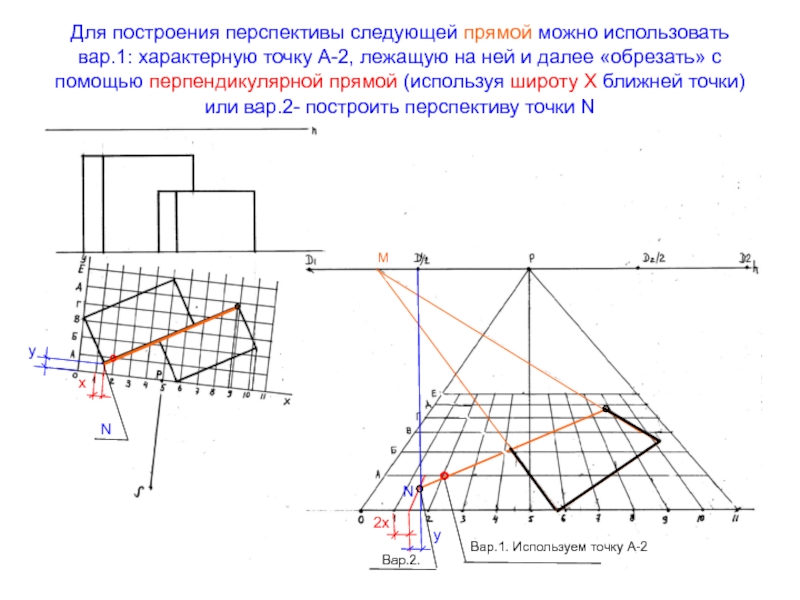
- 53. Для построения перспективы следующей прямой можно
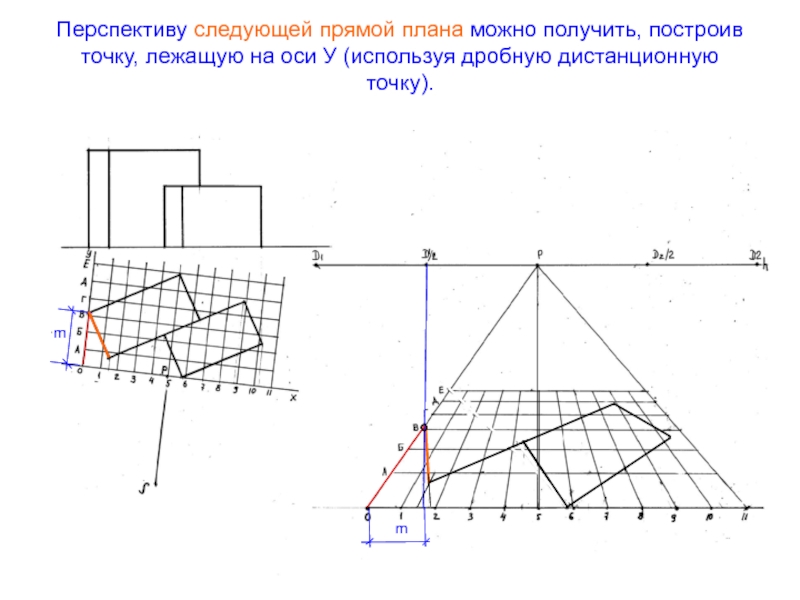
- 54. Перспективу следующей прямой плана можно получить, построив
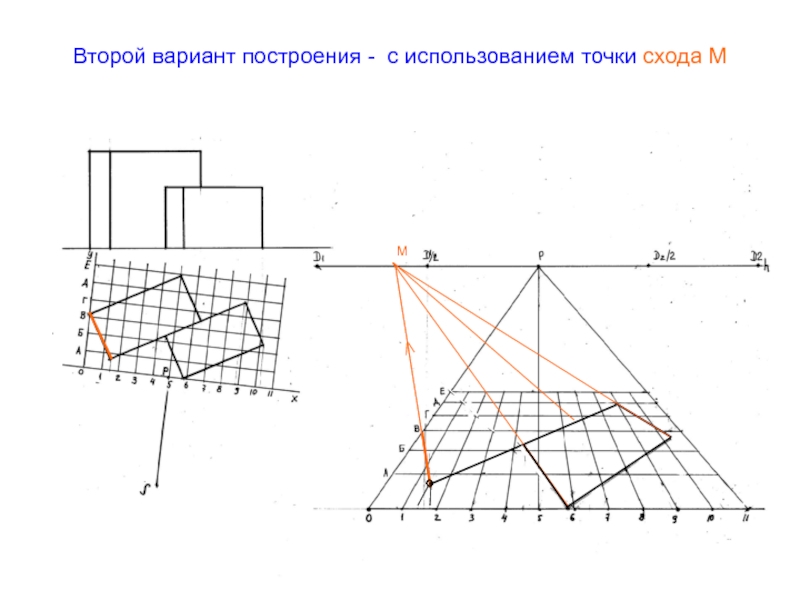
- 55. Второй вариант построения - с использованием точки схода ММ°
- 56. Используя характерную точку Е-5 с помощью точки
- 57. М
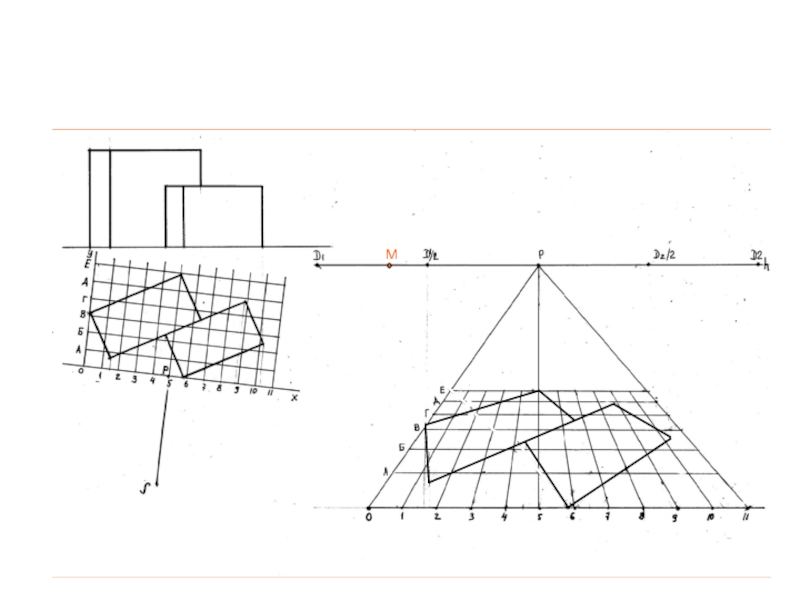
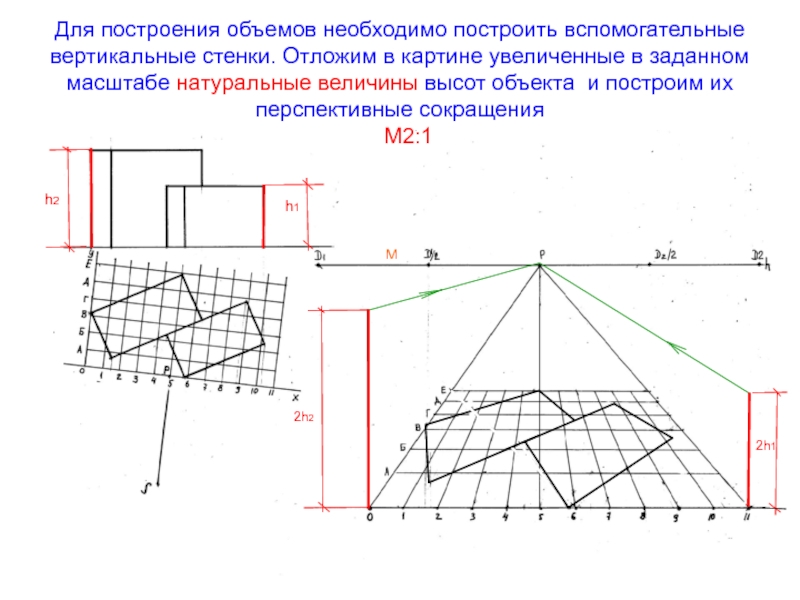
- 58. Для построения объемов необходимо построить вспомогательные
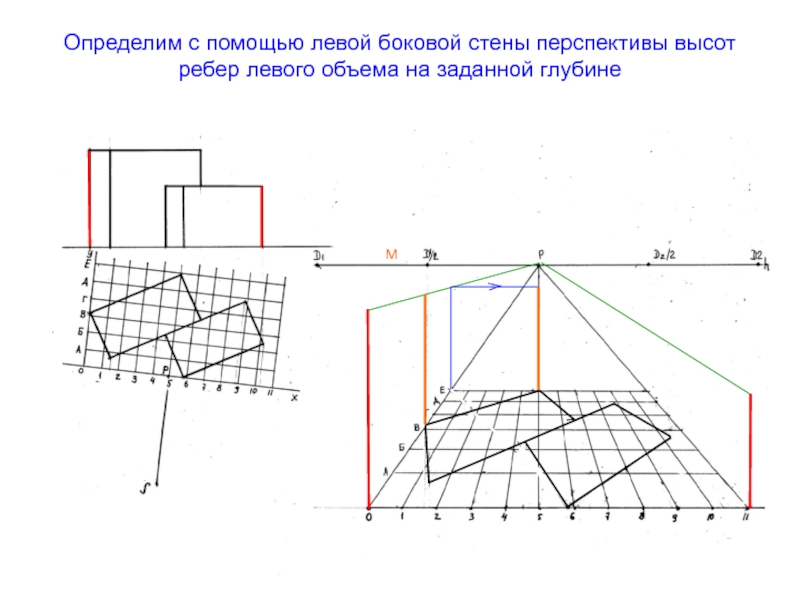
- 59. Определим с помощью левой боковой стены перспективы высот ребер левого объема на заданной глубинеМ
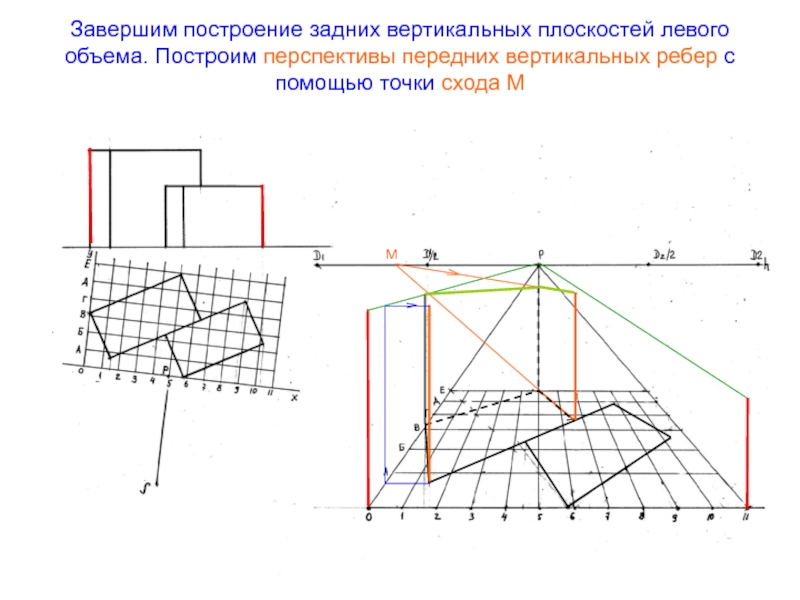
- 60. Завершим построение задних вертикальных плоскостей левого объема.
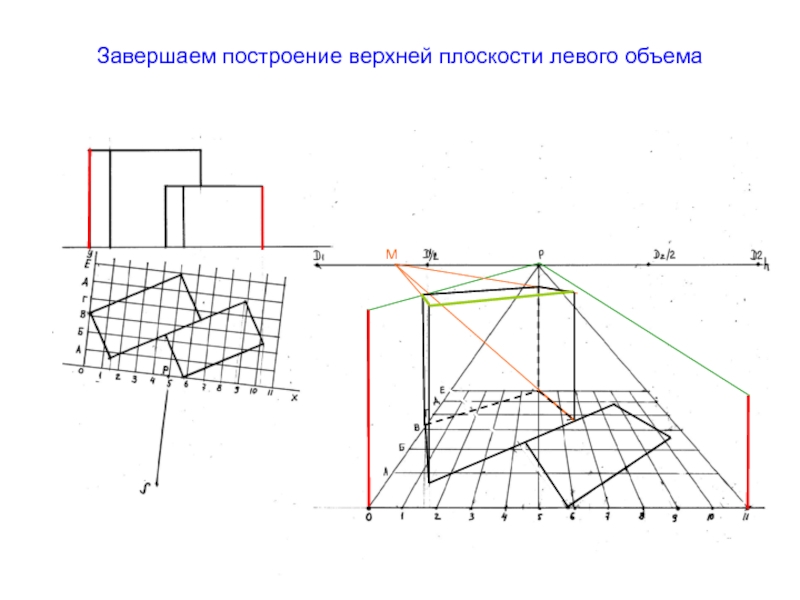
- 61. Завершаем построение верхней плоскости левого объемаМ
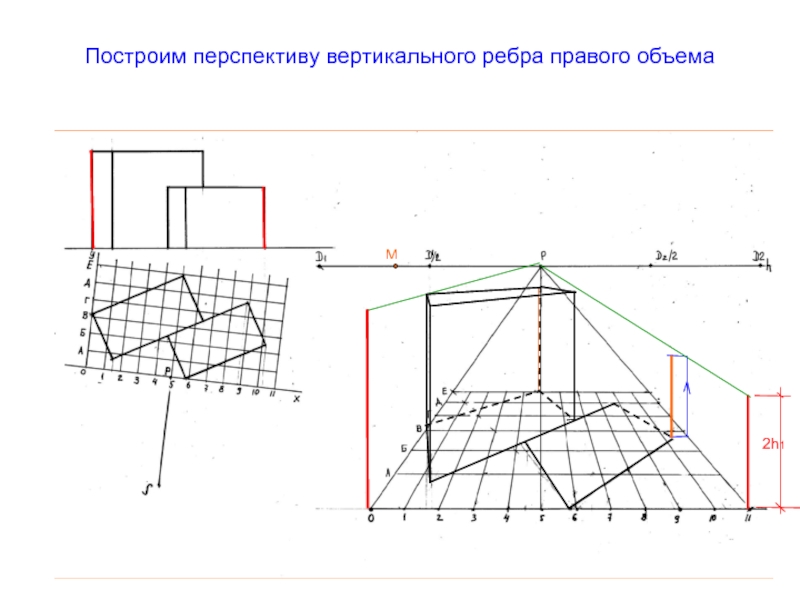
- 62. Построим перспективу вертикального ребра правого объемаМ2h1
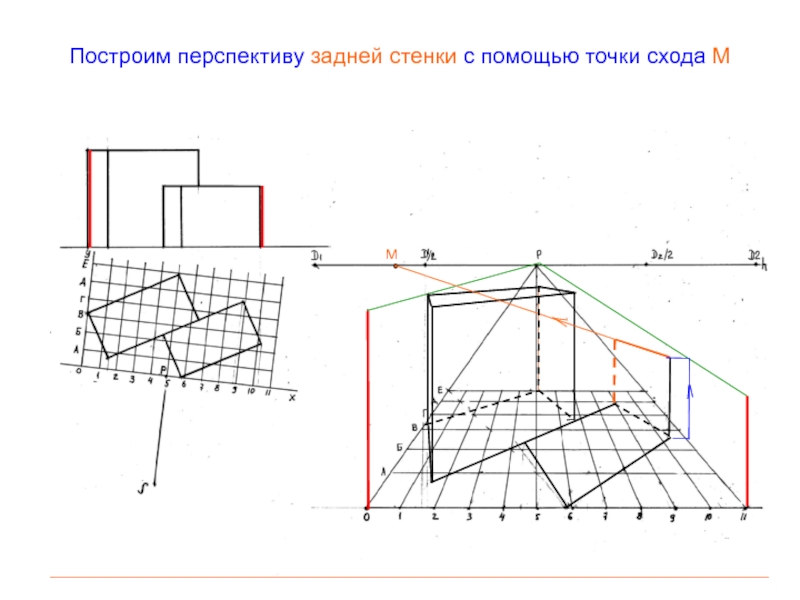
- 63. Построим перспективу задней стенки с помощью точки схода ММ
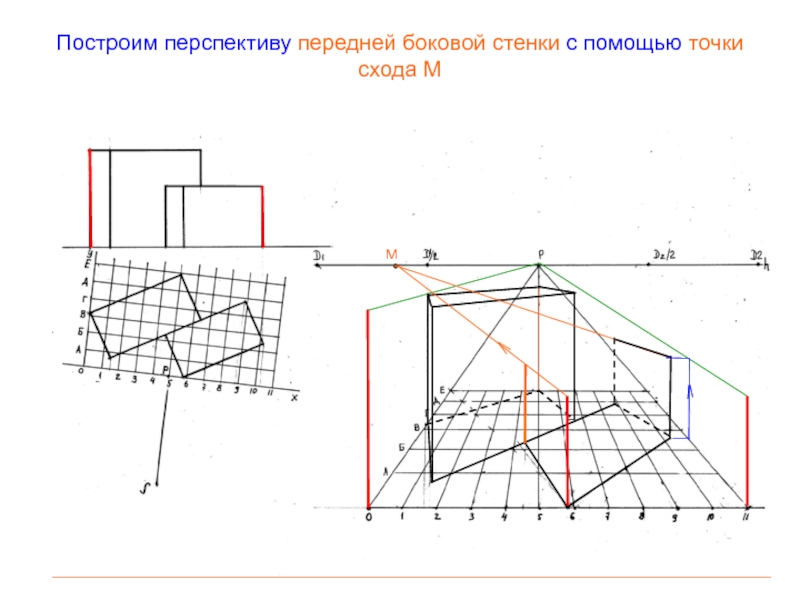
- 64. Построим перспективу передней боковой стенки с помощью точки схода ММ
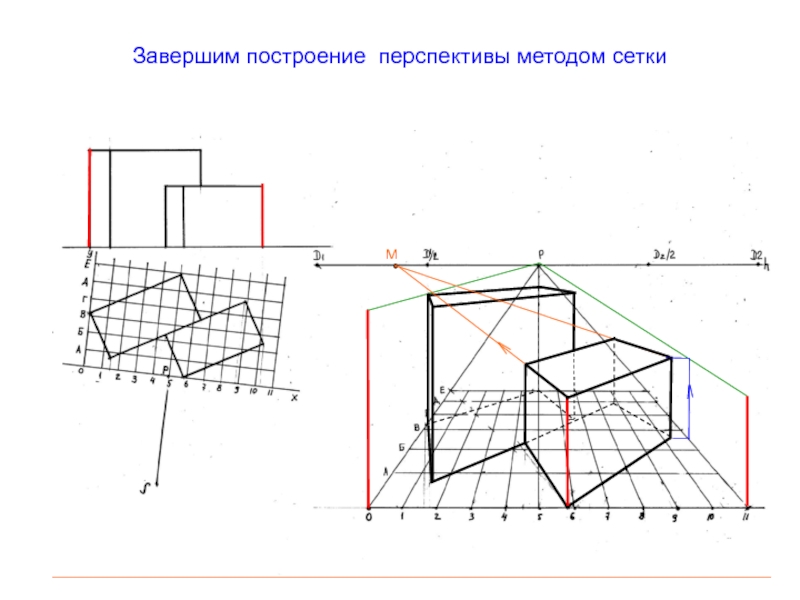
- 65. Завершим построение перспективы методом сеткиМ
- 66. Скачать презентанцию
Координатный способИмеет ограниченное применение. Он используется главным образом при изображении несложных объектов неправильной формы.Сущность этого способа заключается в построении перспективы объекта, отнесенного к прямоугольной системе координат с помощью изображения в перспективе
Слайды и текст этой презентации
Слайд 1Лекция 21
Способ прямоугольных координат и
перспективной сетки
Применение
Сущность способа
Перспективный масштаб
Слайд 2Координатный способ
Имеет ограниченное применение. Он используется главным образом при изображении
несложных объектов неправильной формы.
объекта, отнесенного к прямоугольной системе координат с помощью изображения в перспективе координатной системыСлайд 3Задача:
Построить перспективу прямой АВ
Для построения перспективы объекта на план и
фасад наносят оси прямоугольной системы координат т.о., чтобы картина совпадала
с координат ной плоскостью ХОZ, а предметная плоскость – с координатной плоскостью ХОУСлайд 4
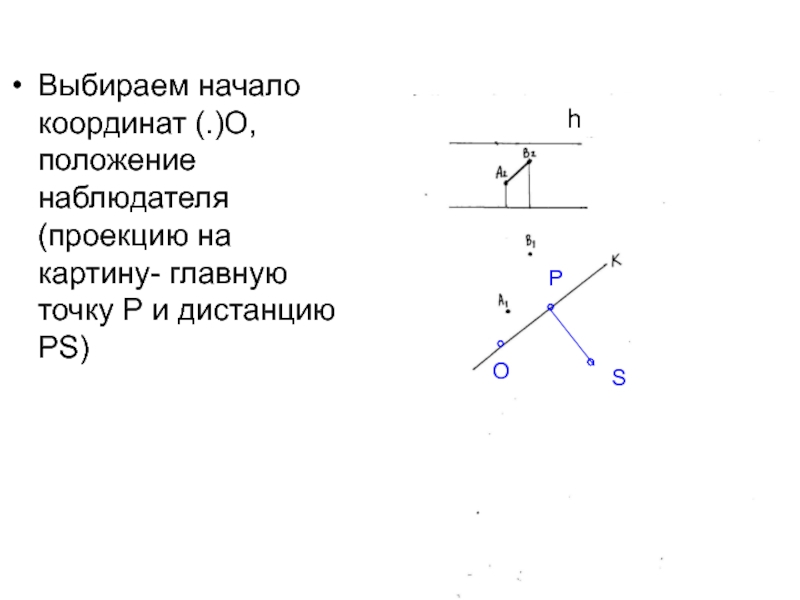
Выбираем начало координат (.)О, положение наблюдателя (проекцию на картину- главную
точку Р и дистанцию РS)
°
°
О
°
Р
S
h
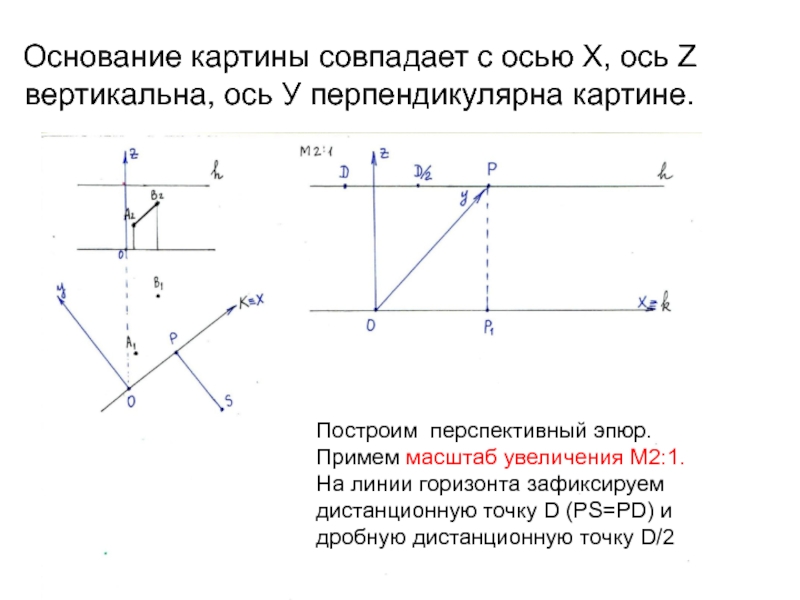
Слайд 5Основание картины совпадает с осью Х, ось Z вертикальна, ось
У перпендикулярна картине.
Построим перспективный эпюр.
Примем масштаб увеличения М2:1.
На линии
горизонта зафиксируем дистанционную точку D (PS=PD) и дробную дистанционную точку D/2Слайд 6Перспективный масштаб
Координатные оси, построенные в перспективе, называются перспективным масштабом
Ось Х-
масштаб широт
Ось У- масштаб глубин
Ось Z- масштаб высот
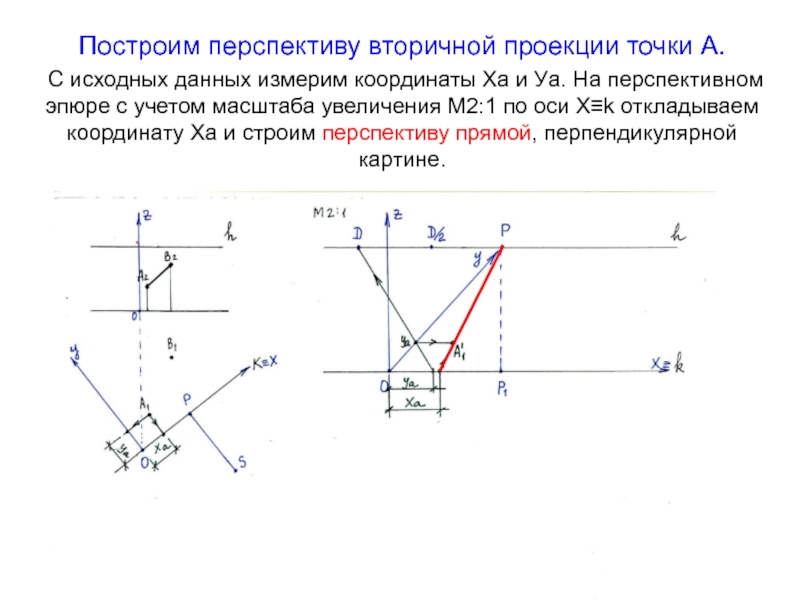
Слайд 7Построим перспективу вторичной проекции точки А. С исходных данных измерим
координаты Ха и Уа. На перспективном эпюре с учетом масштаба
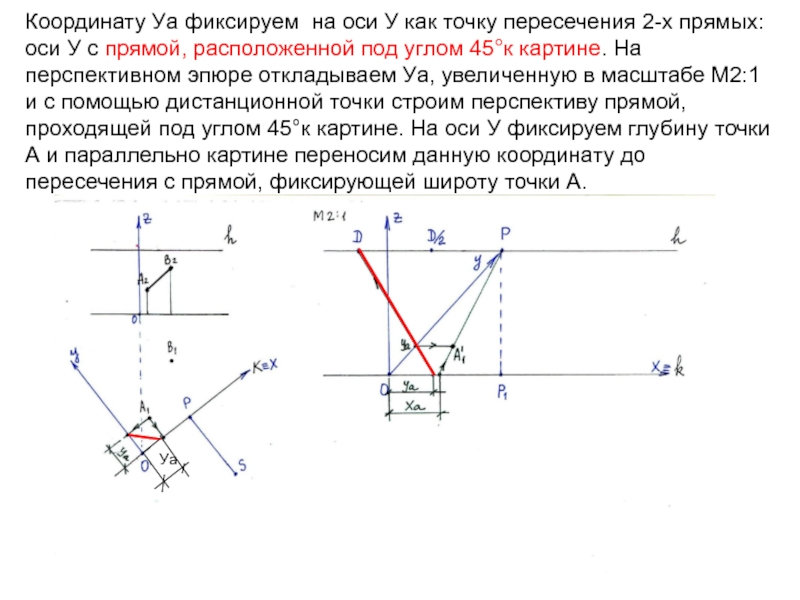
увеличения М2:1 по оси Х≡k откладываем координату Ха и строим перспективу прямой, перпендикулярной картине.Слайд 8Координату Уа фиксируем на оси У как точку пересечения 2-х
прямых: оси У с прямой, расположенной под углом 45°к картине.
На перспективном эпюре откладываем Уа, увеличенную в масштабе М2:1 и с помощью дистанционной точки строим перспективу прямой, проходящей под углом 45°к картине. На оси У фиксируем глубину точки А и параллельно картине переносим данную координату до пересечения с прямой, фиксирующей широту точки А.Уа
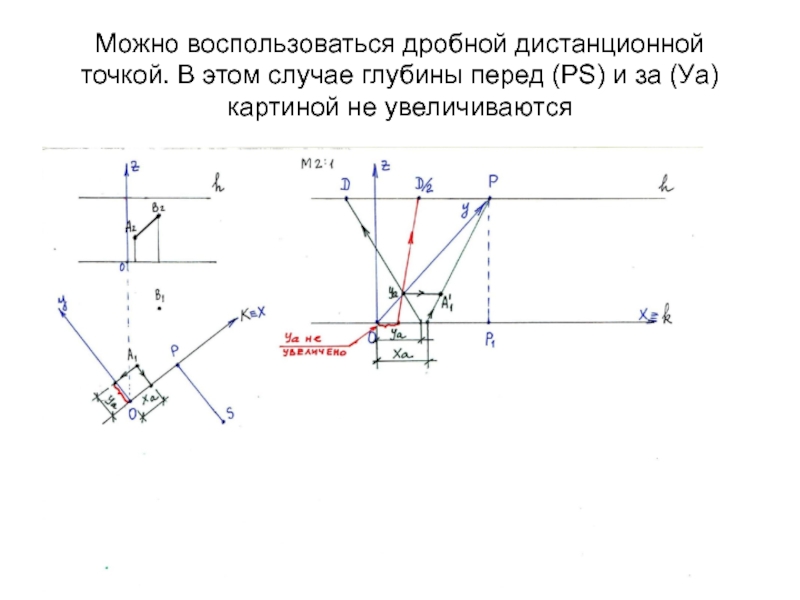
Слайд 9Можно воспользоваться дробной дистанционной точкой. В этом случае глубины перед
(РS) и за (Уа) картиной не увеличиваются
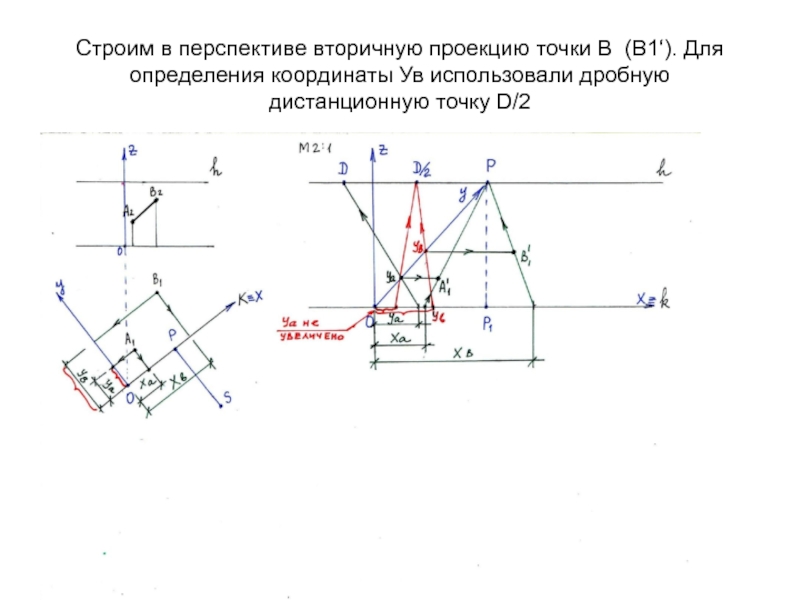
Слайд 10Строим в перспективе вторичную проекцию точки В (В1‘). Для определения
координаты Ув использовали дробную дистанционную точку D/2
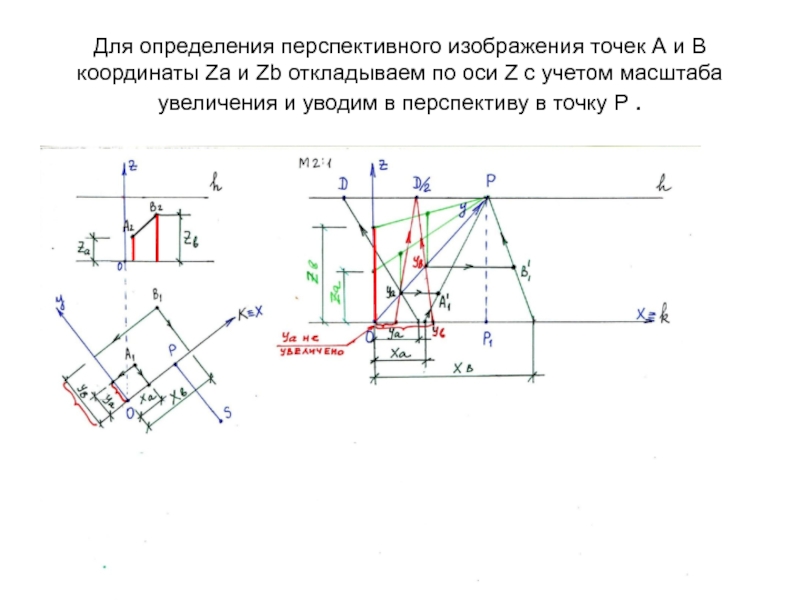
Слайд 11Для определения перспективного изображения точек А и В координаты Za
и Zb откладываем по оси Z с учетом масштаба увеличения
и уводим в перспективу в точку Р .Слайд 12На полученной глубине Уа и Ув определяем размер высоты точек
и переносим их параллельно картине на перпендикуляры, восстановленные в точках
А1‘ и В1‘. Получаем перспективу прямой А'В ' и ее вторичной проекции А1‘ В1‘Слайд 13Способ перспективной сетки
Способ является разновидностью координатного способа
Он основан на применении
перспективных масштабов
Применяют при построении «планировочных» перспектив с высоким горизонтом (перспектива
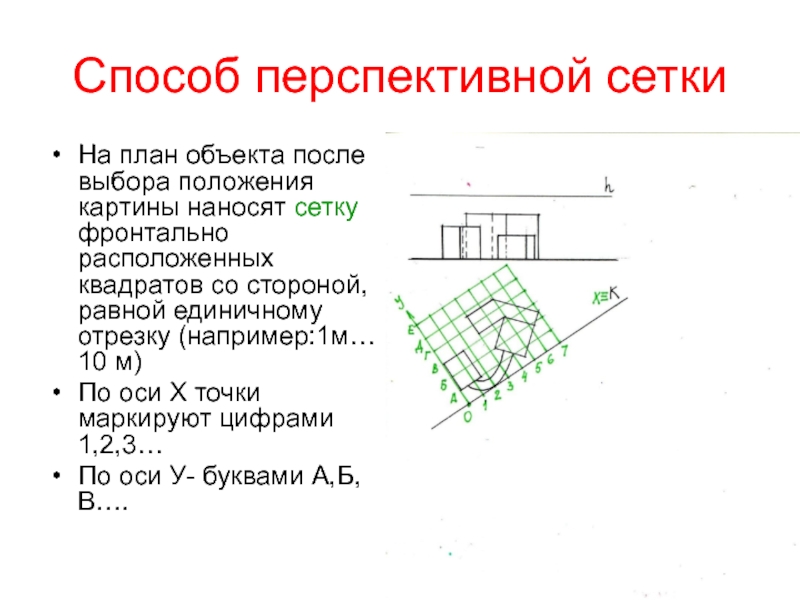
с «птичьего полета») при проектировании градостроительных и промышленных объектов, расположенных на значительной территорииСлайд 14Способ перспективной сетки
На план объекта после выбора положения картины наносят
сетку фронтально расположенных квадратов со стороной, равной единичному отрезку (например:1м…
10 м)По оси Х точки маркируют цифрами 1,2,3…
По оси У- буквами А,Б,В….
Слайд 15Выбирают положение наблюдателя и строят перспективный аппарат. В данном примере
задан масштаб увеличения М 2:1
а
а - единичный модуль
2а
Слайд 16Строим перспективу сетки. По оси Х откладываем единичные отрезки(точки 1,2…7)
с учетом масштаба увеличения и проводим перспективы прямых, перпендикулярных картине
Слайд 17С помощью дистанционной точки D определяем координаты глубин У точек
А,Б…. и проводим прямые, параллельные картине
а
Слайд 18При использовании дробной дистанционной точки расстояния до и после картины
не увеличивают и координату У каждой точки определяют отдельно
а
Слайд 19Т.е. по оси Х откладывают размеры единичных отрезков без увеличения
и с помощью прямых, уходящих в точку схода D/2, определяют
перспективы координат Уа,Уб…..а
Слайд 20Строим перспективу плана объектов. Координаты Х определяем пропорциональным делением широт. Масштаб
широт пропорциональный
Слайд 21Для определения перспектив прямых используем характерные точки, полученные на пересечении
прямых с перспективной сеткой.
°
Слайд 22Например, середину отрезка, уходящего в глубину, можно получить с помощью
диагоналей перспективного квадрата
Слайд 23Cоединив две полученные точки плана, получаем перспективу прямой, уходящей в
недоступную точку схода
Слайд 24Применение теоремы Фалеса о пропорциональном делении отрезка
масштаб глубин непропорциональный.
Для определения
точек, лежащих на прямых, перпендикулярных картине, применяем теорему Фалеса.
Например,
сторону перспективного квадрата по линии 3 между В-Г надо разделить на 3 части. Через конец отрезка на параллельной прямой откладываем пропорцию, равную 3 частям, соединяем конец пропорции с концом отрезка и находим точку схода этой прямой. Переносим пропорцию на искомую прямуюСлайд 25Через найденную с помощью теоремы Фалеса точку на прямой 3
проводим параллельную картине прямую. Аналогично строим параллельную прямую, проходящую между
Д-Г. Строим доступную точку схода для прямой заднего плана, расположенную под углом к картинеСлайд 26С помощью точки схода определяем перспективу второй прямой, определяющей план
заднего объекта
Слайд 27Перспективу высот можно построить, применяя вспомогательные вертикальные плоскости. Учитывая, что
масштаб увеличения принят М2:1, в плоскости картины откладываем высоты объекта
h1, h2 ,h3 и с помощью горизонталей, определяем их перспективное сокращение в плоскостях, перпендикулярных картинеСлайд 29Для построения горизонтальных прямых, расположенных под углом к картине на
заданной высоте, можно с помощью боковой стены определить высоты двух
ее точекСлайд 36Определение высоты объекта
(второй способ)
Высоту объекта можно определить, используя масштабную
шкалу, откладывая размер от вторичной проекции точки параллельно поперечным линиям
сеткиСлайд 39Зададим картину под углом 30° к плоскости главного фасада через
ребро объекта. Наложим систему координат
≡к
30°
Слайд 40 На оси Х отложим единичные отрезки и замаркируем цифрами.
Проведем прямые, перпендикулярные картине
Слайд 41На оси У отложим единичные отрезки и замаркируем буквами. Проведем
прямые, параллельные картине. Получим координатную сетку
Слайд 44 Определим масштаб увеличения перспективного изображения. В данном случае выбран М
2:1. На линии горизонта отложим точки Р, дистанционные и дробные
дистанционные точки. На основании картины зафиксируем начало координат и отложим единичные отрезкиМ 2:1
Р1≡
а
в
2в
2а
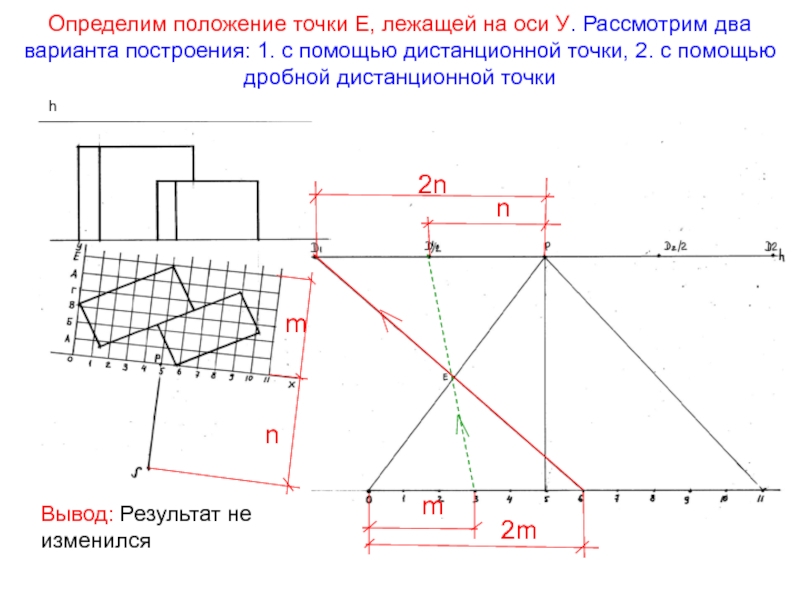
Слайд 46Определим положение точки Е, лежащей на оси У. Рассмотрим два
варианта построения: 1. с помощью дистанционной точки, 2. с помощью
дробной дистанционной точкиh
m
2m
m
n
2n
n
Вывод: Результат не изменился
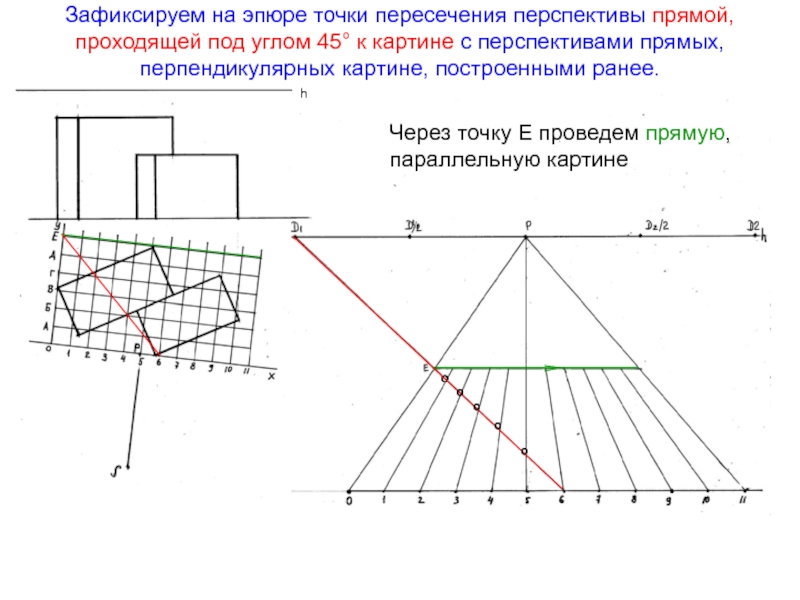
Слайд 47Зафиксируем на эпюре точки пересечения перспективы прямой, проходящей под углом
45° к картине с перспективами прямых, перпендикулярных картине, построенными ранее.
h
°
°
°
°
°
Через
точку Е проведем прямую,параллельную картине
Слайд 48Через полученные точки проведем перспективы прямых, параллельных картине, и завершим
построение перспективной масштабной сетки
°
°
°
°
°
Слайд 49Далее положение точки можно зафиксировать различными способами. Например, с помощью
прямой, перпендикулярной картине и прямой под углом 45° к картине
а
а
2а
°
в
2в
а
Слайд 51Аналогично построим перспективу следующей точки и определим перспективу второй прямой
плана
М
у
х
2х
у
°
°
Слайд 52Построим точку схода М полученной прямой и определим направление перспективы
следующей прямой
М
у
х
2х
у
Слайд 53 Для построения перспективы следующей прямой можно использовать вар.1: характерную точку
А-2, лежащую на ней и далее «обрезать» с помощью перпендикулярной
прямой (используя широту Х ближней точки) или вар.2- построить перспективу точки NМ
у
у
°
х
2х
°
°
°
Вар.1. Используем точку А-2
Вар.2.
°
N
N
Слайд 54Перспективу следующей прямой плана можно получить, построив точку, лежащую на
оси У (используя дробную дистанционную точку).
m
m
°
Слайд 56Используя характерную точку Е-5 с помощью точки схода М построим
перспективу следующей прямой и завершим построение плана
М
°
°
°
Слайд 58 Для построения объемов необходимо построить вспомогательные вертикальные стенки. Отложим в
картине увеличенные в заданном масштабе натуральные величины высот объекта и
построим их перспективные сокращенияМ
h1
h2
2h2
2h1
М2:1