Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЛЕКЦИЯ 3в Червячные передачи
Содержание
- 1. ЛЕКЦИЯ 3в Червячные передачи
- 2. Гиперболические передачи. Краткие сведения.
- 3. Червячная передача
- 4. Движение в червячной передачепреобразуется по принципу винтовой пары.Изобретателем червячных передач считают Архимеда.
- 5. Слайд 5
- 6. Достоинства червячных передач: компактность
- 7. Основной недостаток червячных
- 8. Кроме того, помимо
- 9. Передаточное отношение червячной передачи находят
- 10. Очевидно, что однозаходный червяк
- 11. Основные причины выхода из строя червячных передач: поверхностное выкрашивание и схватывание (слипание);- излом зуба.
- 12. Классификация червячных передач:
- 13. по направлению линии витка червяка:1.1. правые (при
- 14. по числу заходов червяка: 2.1. с однозаходным
- 15. по форме делительной поверхности червяка: 3.1.
- 16. по положению червяка относительно червячного колеса:4.1. с
- 17. по пространственному положению вала червячного колеса:5.1. с горизонтальным валом червячного колеса;5.2. с вертикальным валом червячного колеса;
- 18. по форме рабочей поверхности витка червяка: 6.1.
- 19. Архимедовы в осевом сечении имеет трапецеидальный профиль резьбы.
- 20. конволюнтные имеет трапецеидальный профиль резьбы в нормальном
- 21. Червяки
- 22. В глобоидной передаче
- 23. Слайд 23
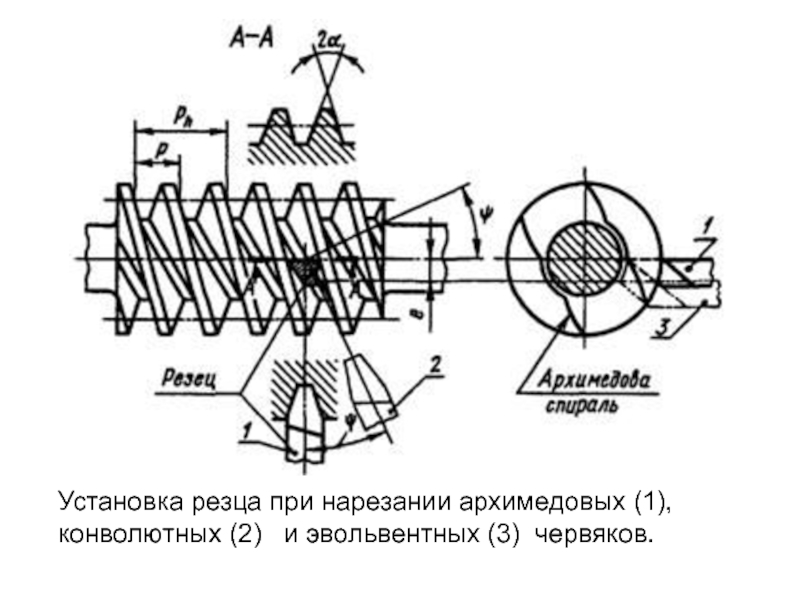
- 24. Установка резца при нарезании архимедовых (1), конволютных (2) и эвольвентных (3) червяков.
- 25. Геометрические характеристики червячной
- 26. Слайд 26
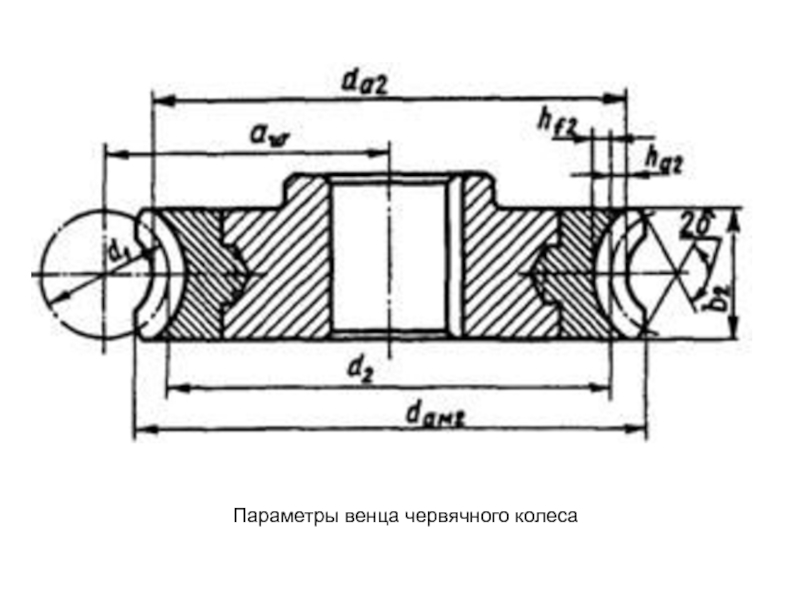
- 27. Параметры венца червячного колеса
- 28. Слайд 28
- 29. В осевом сечении
- 30. Слайд 30
- 31. Основным стандартизованным параметром
- 32. Учитывая изложенное, модуль с делительными диаметрами червяка и червячного колеса связан соотношениями:
- 33. Расстояние, измеренное между
- 34. Расстояние, измеренное между одноименными
- 35. Высота головок витков
- 36. Тогда диаметр вершин витков
- 37. Диаметр впадин витков (внутренний
- 38. Измеренный в плоскости
- 39. Длина нарезанной части червяка b1
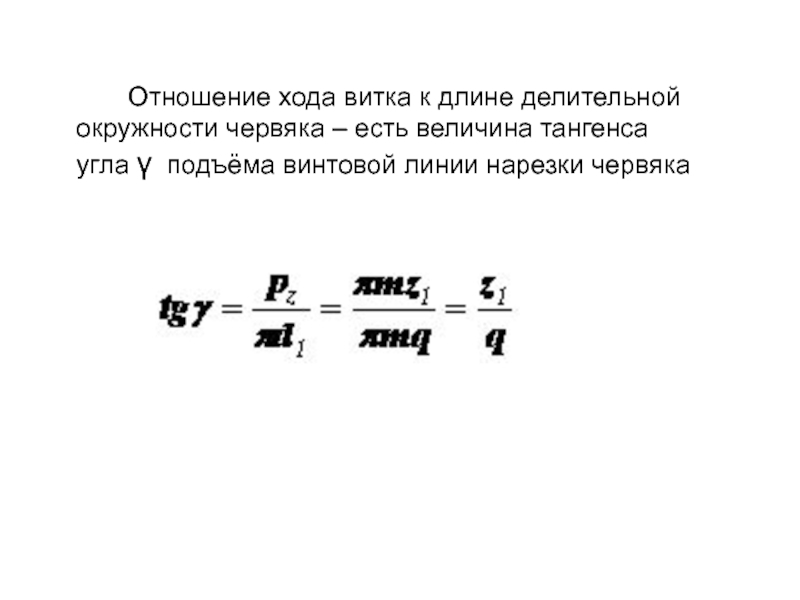
- 40. Отношение хода витка
- 41. Ширину зубчатого венца
- 42. При прочностных расчетах червячной
- 43. Межосевое расстояние для несмещенной червячной передачи определяется по формуле
- 44. зависимость для вычисления передаточного
- 45. В червячной передаче, в
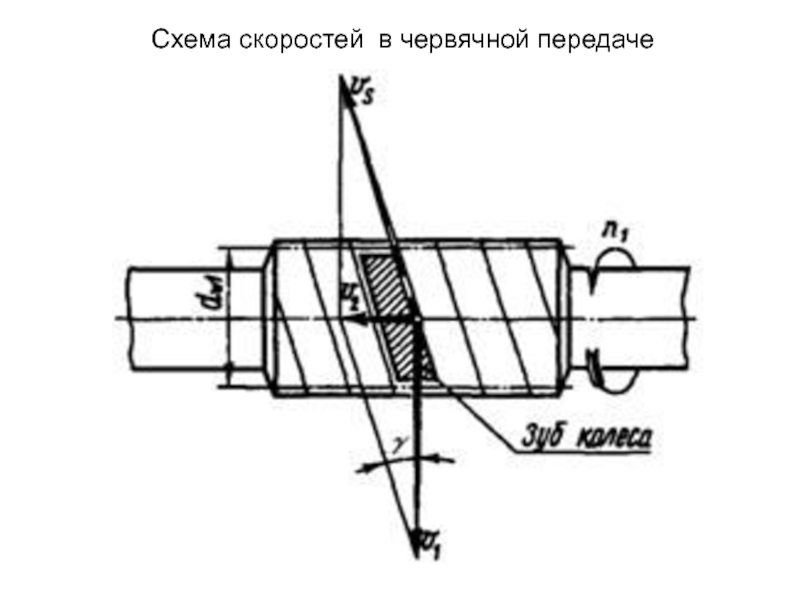
- 46. Схема скоростей в червячной передаче
- 47. Геометрическая сумма скоростей v1
- 48. Коэффициент полезного действия ηз червячного
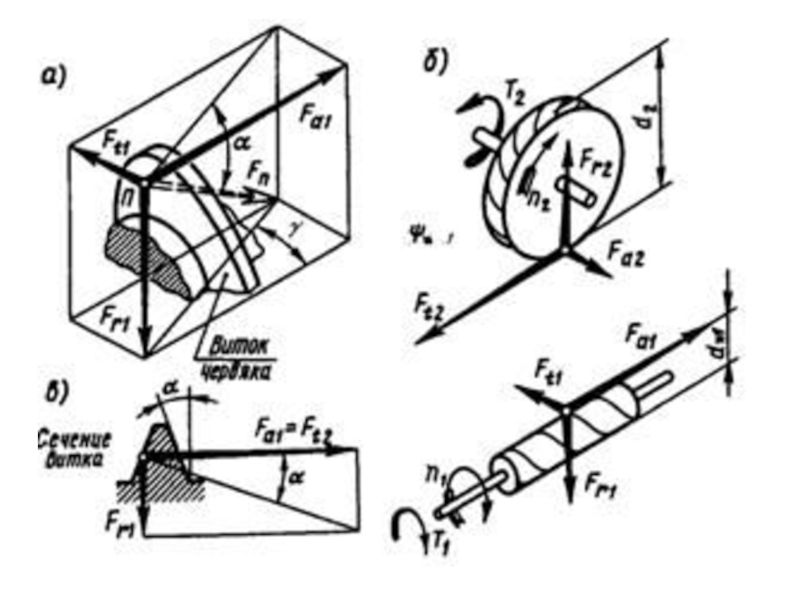
- 49. Силы в червячной передаче
- 50. Слайд 50
- 51. В червячной передаче сила
- 52. Тангенциальные силы
- 53. Виды разрушения червячных передач:Износ рабочих поверхностей колеса
- 54. Ввиду высоких скоростей скольжения
- 55. Витки червяка и
- 56. 1. качественные среднеуглеродистые стали марок
- 57. 2. Среднеуглеродистые легированные стали марок
- 58. 3. Мало- и среднеуглеродистые легированные
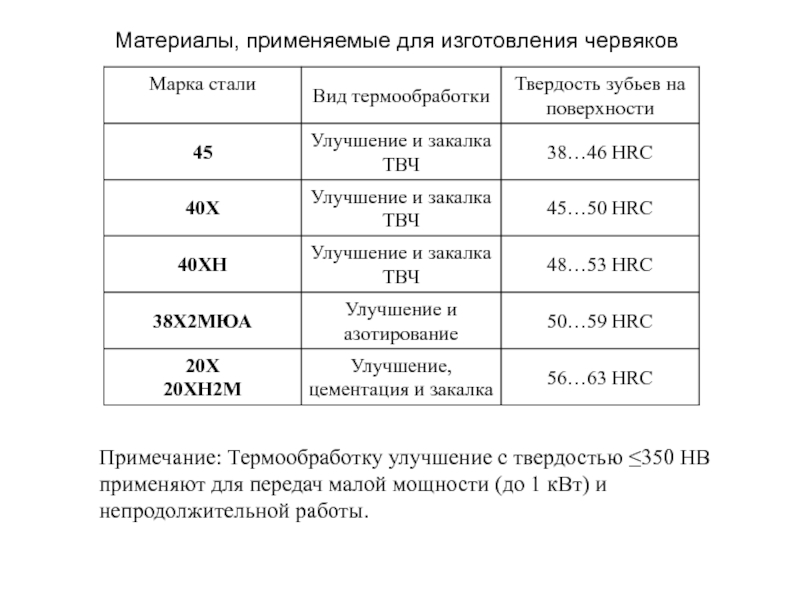
- 59. Материалы, применяемые для изготовления червяковПримечание: Термообработку улучшение
- 60. Материалы зубчатых венцов червячных
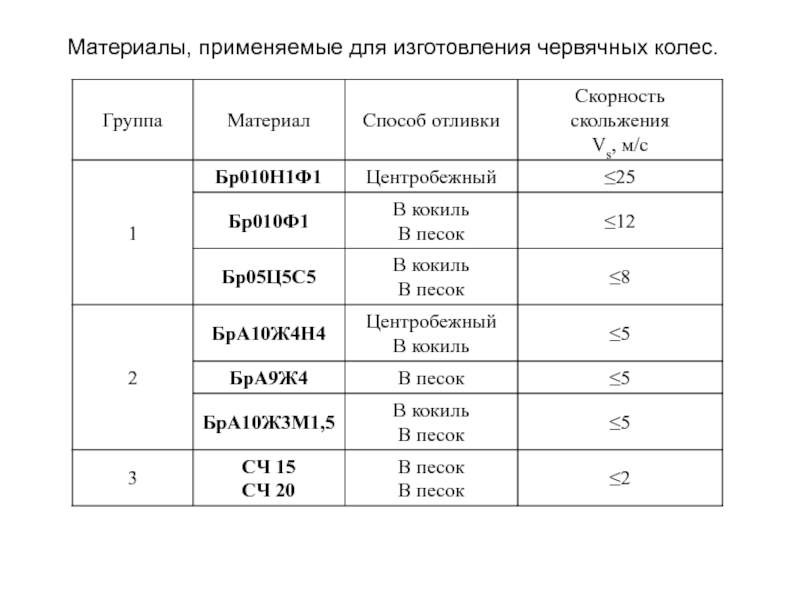
- 61. 1 группа - оловянные бронзы. Применяют при
- 62. Зубчатые венцы червячных
- 63. При средних скоростях скольжения
- 64. В передачах с
- 65. Материалы, применяемые для изготовления червячных колес.
- 66. Слайд 66
- 67. Бронзовые венцы червячных
- 68. Цветные металлы дороги
- 69. Слайд 69
- 70. Заготовка для зубчатого венца
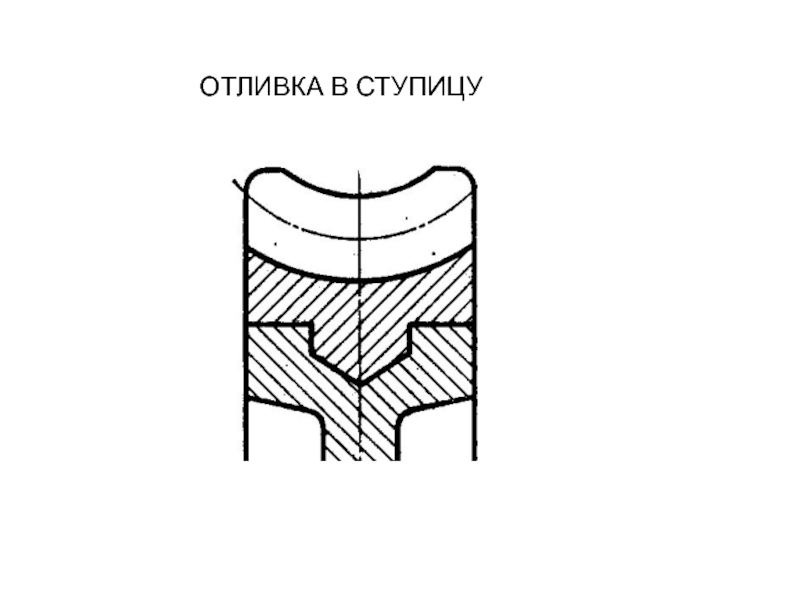
- 71. ОТЛИВКА В СТУПИЦУ
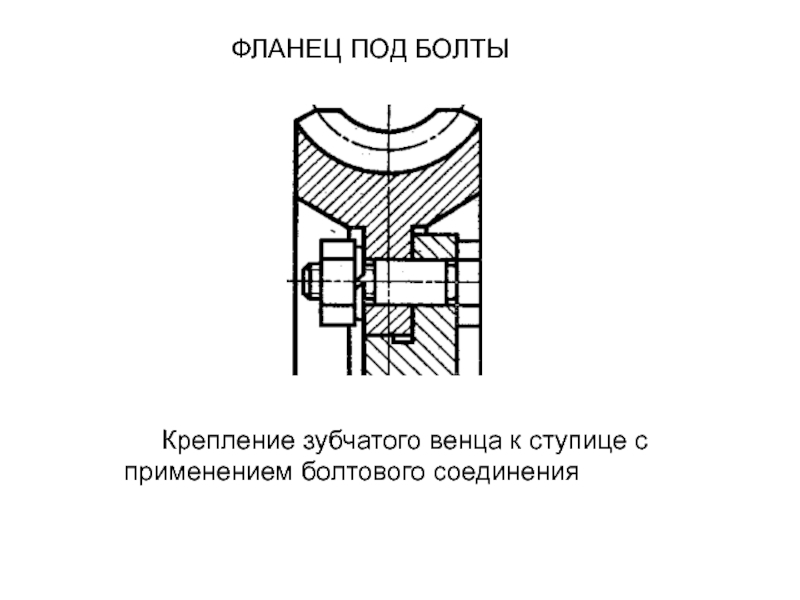
- 72. ФЛАНЕЦ ПОД БОЛТЫ Крепление зубчатого венца к ступице с применением болтового соединения
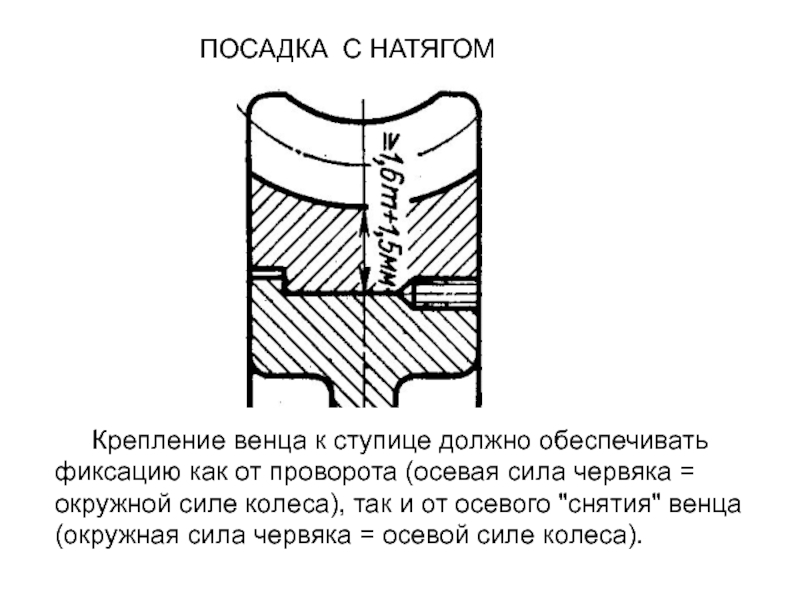
- 73. ПОСАДКА С НАТЯГОМ Крепление венца
- 74. Размеры и долговечность
- 75. При чрезмерных кратковременных перегрузках
- 76. Исходя из вышесказанного,
- 77. Считается, что расчет на
- 78. Расчет зубьев на выносливость по контактным напряжениям
- 79. В основу расчета
- 80. Формула проектного расчета
- 81. Формулы проверочного расчета- по контактным напряжениям - по напряжениям изгиба
- 82. СПАСИБО ЗА ВНИМАНИЕ
- 83. Скачать презентанцию
Гиперболические передачи. Краткие сведения. Механика червячной передачи и расчет. Материалы и допускаемые напряжения.
Слайды и текст этой презентации
Слайд 2 Гиперболические передачи.
Краткие сведения. Механика червячной передачи
и расчет. Материалы и допускаемые напряжения.
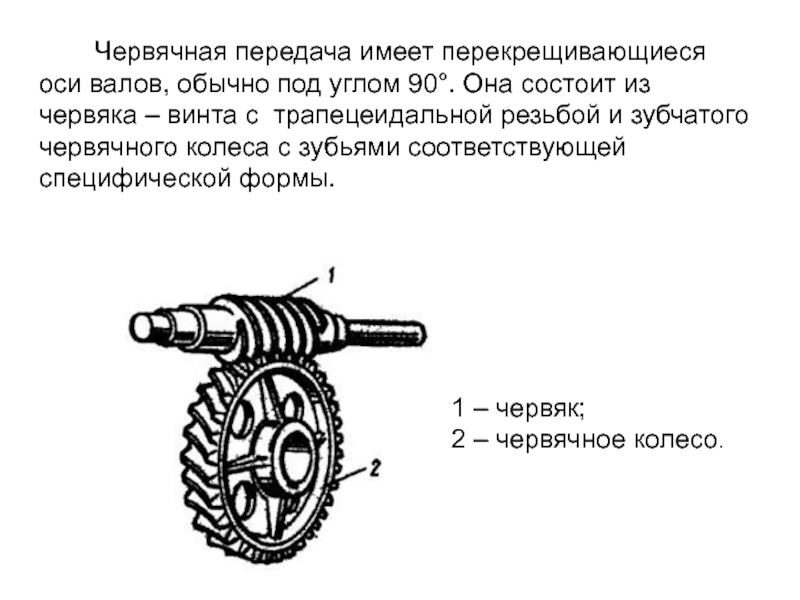
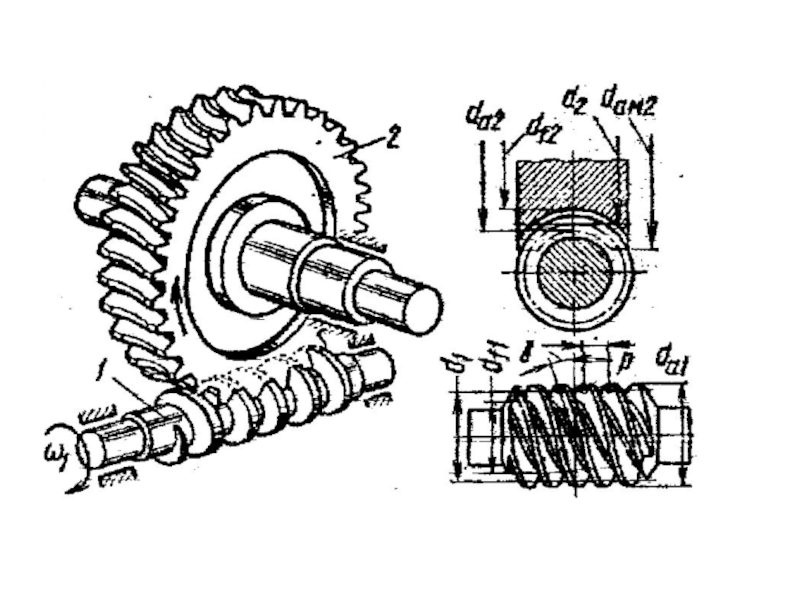
Слайд 3 Червячная передача имеет перекрещивающиеся оси
валов, обычно под углом 90°. Она состоит из червяка –
винта с трапецеидальной резьбой и зубчатого червячного колеса с зубьями соответствующей специфической формы.1 – червяк;
2 – червячное колесо.
Слайд 4 Движение в червячной передаче
преобразуется по принципу винтовой
пары.
Изобретателем червячных передач считают Архимеда.
Слайд 6 Достоинства червячных передач:
компактность и относительно небольшая
масса конструкции;
2) возможность получения больших передаточных чисел в одной
ступени – стандартные передачи u = 8 - 80, специальные - до 300; 3) высокая плавность и кинематическая точность;
4) низкий уровень шума и вибраций;
5) самоторможение при обратной передаче движения, то есть невозможность передачи движения в обратном направлении - от ведомого червячного колеса к ведущему червяку.
Слайд 7 Основной недостаток червячных передач – высокое
трение в зацеплении и как следствие:
низкий КПД (на 20-30% ниже,
чем у зубчатых);высокое тепловыделение;
повышенный износ и уменьшенный срок службы;
склонность к заеданию, что вызывает необходимость применения специальных дорогостоящих антифрикционных материалов для изготовления зубчатого венца червячного колеса и специальных видов смазки с антизадирными присадками.
Слайд 8 Кроме того, помимо достоинств и недостатков,
червячные передачи имеют важное свойство:
движение передаётся только от червяка
к колесу, а не наоборот. Именно поэтому червячные передачи находят применение в подъёмных механизмах, например в лифтах. Там электродвигатель соединён с червяком, а трос пассажирской кабины намотан на вал червячного колеса во избежание самопроизвольного опускания или падения.
Слайд 9 Передаточное отношение червячной передачи находят аналогично цилиндрической
U
= n1 / n2 = Z2 / Z1.
здесь Z2 –
число зубьев колеса, а роль числа зубьев шестерни Z1 выполняет число заходов червяка, которое обычно бывает равно 1, 2, 3 или 4.
Слайд 10 Очевидно, что однозаходный червяк даёт наибольшее передаточное
отношение, однако наивысший КПД достигается при многозаходных
червяках, что связано с
уменьшением трения за счёт роста угла трения.
Слайд 11Основные причины выхода из строя червячных передач:
поверхностное выкрашивание и
схватывание
(слипание);
- излом зуба.
Слайд 13
по направлению линии витка червяка:
1.1. правые (при наблюдении с торца
червяка и его вращении по часовой стрелке червяк вкручивается в
пространство - уходит от наблюдателя);1.2. левые (при наблюдении с торца червяка и его вращении по часовой стрелке червяк выкручивается из пространства - идёт на наблюдателя);
Слайд 14по числу заходов червяка:
2.1. с однозаходным червяком, имеющим один
гребень, расположенный по винтовой линии, наложенной на делительный цилиндр червяка;
2.2.
с двух-, трёх-, четырёх-, многозаходным червяком, имеющим соответственно 2, 3, 4 или более одинаковых гребней расположенных по винтовой линии, наложенной на делительный цилиндр червяка;
Слайд 15по форме делительной поверхности червяка:
3.1. с цилиндрическим червяком
(образующая делительной поверхности – прямая линия);
3.2. с глобоидным
червяком (образующая делительной поверхности – дуга окружности, совпадающая с окружностью делительной поверхности червячного колеса);
Слайд 16по положению червяка относительно червячного колеса:
4.1. с нижним расположением червяка;
4.2.
с верхним расположением червяка;
4.3. с боковым расположением червяка;
Слайд 17по пространственному положению вала червячного колеса:
5.1. с горизонтальным валом червячного
колеса;
5.2. с вертикальным валом червячного колеса;
Слайд 18по форме рабочей поверхности витка червяка:
6.1. с архимедовым червяком,
боковая поверхность его витков очерчена прямой линией в продольно-диаметральном сечении
(обозначается ZA);6.2. с конволютным червяком, боковая поверхность его витков очерчена прямой линией в нормальном к направлению витков сечении (обозначается ZN);
6.3. с эвольвентным червяком, боковая поверхность его витков в продольно-диаметральном сечении очерчена эвольвентой (обозначается ZI).
6.4 с вогнутым профилем витков резьбы.
Слайд 20конволюнтные имеет трапецеидальный профиль резьбы в нормальном сечении витков; эвольвентные -
характеризуется тем, что профиль резьбы в его осевом сечении эвольвентный;
В передачах с архимедовыми, конволютными и эвольвентными червяками профиль зубьев червячных колес эвольвентный. Модули эвольвентных червячных передач стандартизованы.
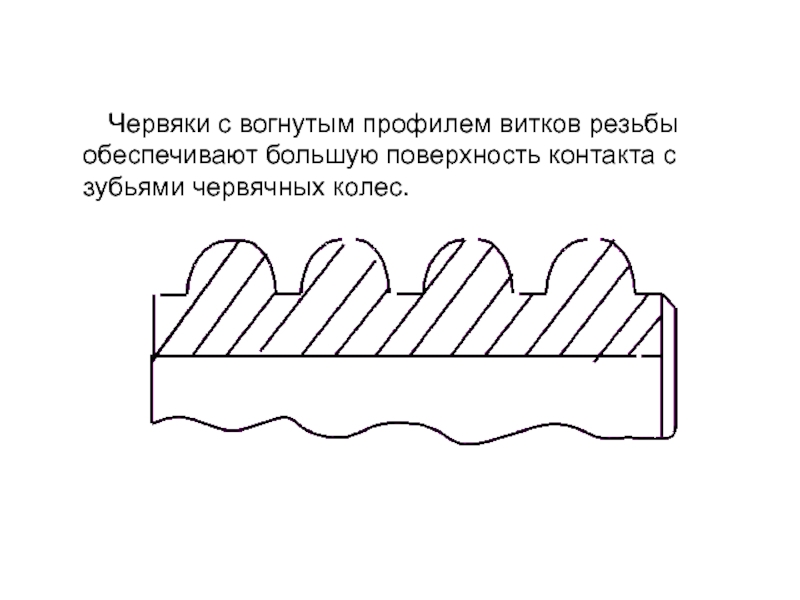
Слайд 21 Червяки с вогнутым профилем витков резьбы
обеспечивают большую поверхность контакта с зубьями червячных колес.
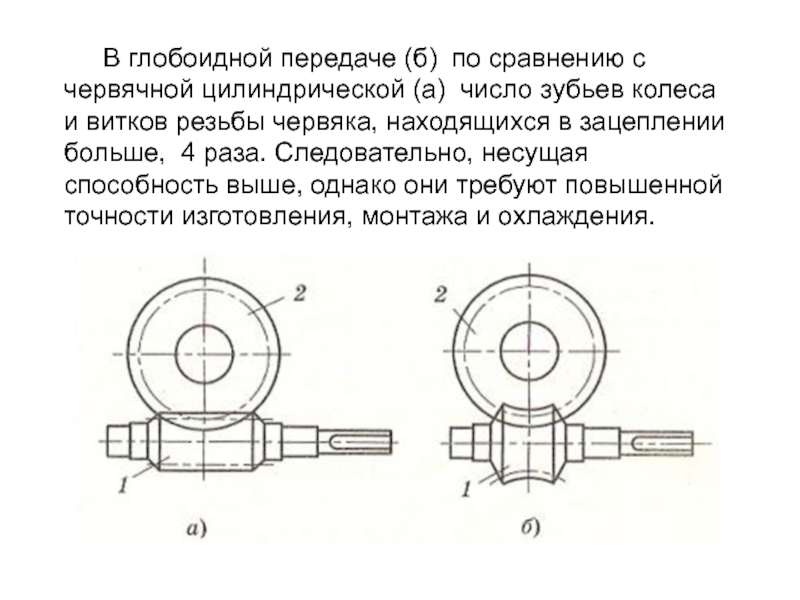
Слайд 22 В глобоидной передаче (б) по сравнению
с червячной цилиндрической (а) число зубьев колеса и витков резьбы
червяка, находящихся в зацеплении больше, 4 раза. Следовательно, несущая способность выше, однако они требуют повышенной точности изготовления, монтажа и охлаждения.
Слайд 23 Эвольвентный червяк эквивалентен
цилиндрическому эвольвентному косозубому колесу с числом зубьев, равным числу заходов
червяка. Форма боковой поверхности червяка мало влияет на работоспособность червячной передачи и, в основном, связана с выбранной технологией изготовления червяка
Слайд 25 Геометрические характеристики червячной передачи связаны между
собой соотношениями, во многом аналогичными соотношениям зубчатых передач.
Слайд 29 В осевом сечении червячная пара фактически
представляет собой прямобочное реечное зацепление, где радиус кривизны боковой поверхности
"рейки" (винта червяка) r1 равен бесконечности и, следовательно, приведённый радиус кривизны равен радиусу кривизны зуба колеса
Слайд 31 Основным стандартизованным параметром червячной передачи является
модуль m (измеряется в мм), осевой для червяка
и окружной (торцовый) для червячного колеса.Поскольку делительный диаметр червяка невозможно связать с числом его заходов z1 (витки червяка нарезаются вдоль его оси, а не по окружности, как у зубчатого колеса), для определения делительного диаметра червяка вводится специальный коэффициент диаметра червяка q, показывающий число модулей, укладывающихся в делительный диаметр.
Слайд 32Учитывая изложенное, модуль с делительными диаметрами червяка и червячного колеса
связан соотношениями:
Слайд 33 Расстояние, измеренное между одноименными поверхностями двух
соседних гребней нарезки червяка, называют расчетным шагом нарезки червяка.
Расчетный шаг нарезки червяка связан с модулем червячного зацепления соотношением, аналогичным таковому для зубчатого зацепления:.
Слайд 34 Расстояние, измеренное между одноименными поверхностями двух соседних
гребней, принадлежащих общей винтовой линии нарезки червяка, называют ходом витка
червяка.Из определения следует, что расчетный шаг p и ход витка pz связаны соотношением
Слайд 35 Высота головок витков червяка и зубьев
червячного колеса также как и в зубчатом зацеплении равна модулю
зацепления (ha1 = ha2 = m), а высота ножек с целью исключения возможности утыкания головки зуба в дно впадины, как и в конических передачах, на 20% больше модуля зацепления (hf1 = hf2 = 1,2m).
Слайд 36 Тогда диаметр вершин витков (внешний диаметр) червяка
da1 и диаметр вершин зубьев червячного колеса da2 могут быть
найдены по выражениям:;
Слайд 37 Диаметр впадин витков (внутренний диаметр) червяка df1
и диаметр впадин зубьев червячного колеса df2 - по выражениям
.
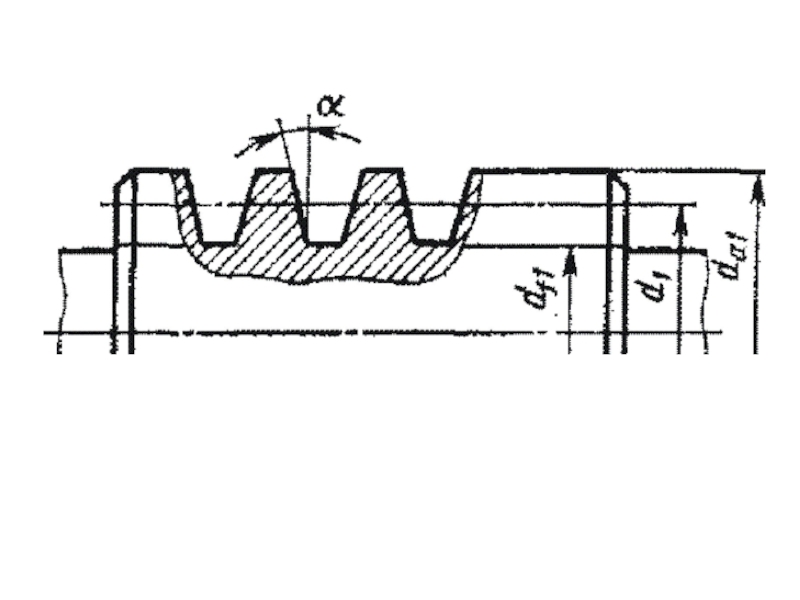
Слайд 38 Измеренный в плоскости осевого сечения угол
α между касательной к боковой поверхности витков червяка и нормалью
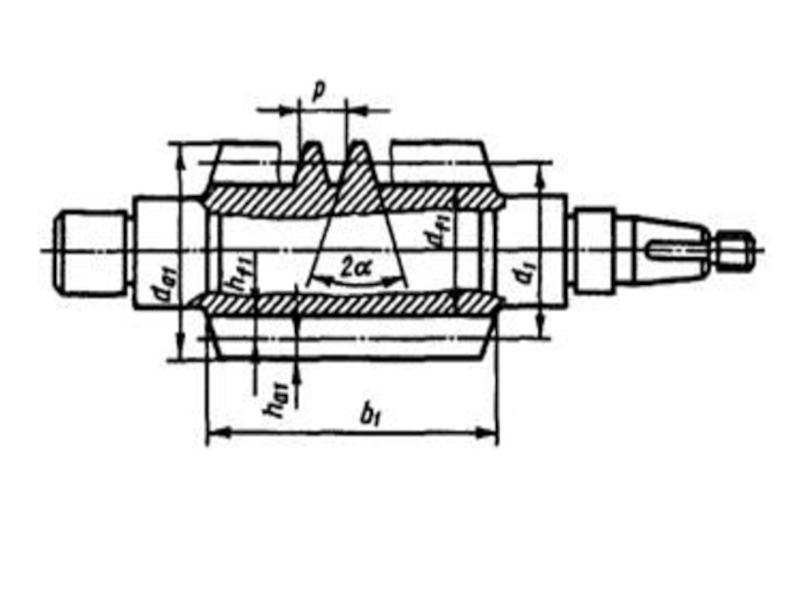
к оси его вращения для архимедовых червяков является величиной постоянной, стандартизован и равен 20°. Следовательно, угол между двумя касательными к противоположным боковым поверхностям одного витка (угол заострения гребня) составляет 2α или 40°.
Слайд 39 Длина нарезанной части червяка b1 зависит от числа
его заходов и выбирается по эмпирической формуле:
а при числе витков
червяка z1 = 4[3]
при числе витков червяка z1 = 1 и z1 = 2 ;
Слайд 40 Отношение хода витка к длине делительной
окружности червяка – есть величина тангенса угла γ подъёма винтовой
линии нарезки червяка
Слайд 41 Ширину зубчатого венца червячного колеса b2
выбирают по стандартному ряду размеров. При этом размер b2 должен
удовлетворять соотношениюпри числе витков червяка z1 = 1 и z1 = 2
а при числе витков червяка z1 = 4
Слайд 42 При прочностных расчетах червячной передачи возникает потребность
в знании условного угла 2δ охвата витков червяка зубьями червячного
колеса..
Слайд 45 В червячной передаче, в отличие от зубчатой,
окружные скорости витков червяка v1 и зубьев червячного колеса v2
различны как по величине, так и по направлению.Витки червяка при его вращении получают скорость v1, направленную по касательной к его начальной окружности, а зубья червячного колеса движутся совместно с винтовой линией параллельно оси червяка со скоростью v2.
Слайд 47 Геометрическая сумма скоростей v1 и v2 равна
скорости относительного движения витков червяка по отношению к зубьям колеса.
План скоростей, построенный для зацепления, позволяет записать следующие зависимости Таким образом, скорость скольжения витков червяка по зубьям червячного колеса является наибольшей по сравнению с тангенциальными скоростями движения витков червяка и зубьев червячного колеса.
Слайд 48 Коэффициент полезного действия ηз червячного зацепления можно вычислить
как КПД винтовой кинематической пары:
где ρ
- угол трения в червячной кинематической паре, а f коэффициент трения для материалов витков червяка и зубчатого венца червячного колеса.
Слайд 51 В червячной передаче сила Fn, действующая со
стороны червяка, воспринимается, как правило, не одним, а несколькими зубьями.
Однако, также как и в зубчатых передачах, при выполнении расчетов эту силу принято располагать в полюсе зацепления.Эту силу не трудно разложить по правилу параллелограмма на три взаимно перпендикулярных составляющих Ft1, Fr1 и Fa1. Далее, согласно третьему закону Ньютона устанавливаем, что
Ft2 = Fa1, Fa2 = Ft1 и Fr2 = Fr1.
Слайд 52 Тангенциальные силы на червяке и
червячном колесе наиболее удобно вычислить через вращающие моменты на соответствующих
валах, тогда
Радиальные силы на червяке и колесе
Слайд 53Виды разрушения червячных передач:
Износ рабочих поверхностей колеса и червяка.
Заедание (в
основном в передачах с колесами из материалов 2 и 3
групп).Усталостное выкрашивание рабочих поверхностей зубьев колеса (только в передачах с колесами из материалов 1 группы).
Усталостные поломки зубьев колеса. Имеют место сравнительно редко, главным образом после значительного износа.
Слайд 54 Ввиду высоких скоростей скольжения и неблагоприятных условий
гидродинамической связки в зоне зацепления, червячные колеса изготавливают из материалов,
обладающих хорошими антифрикционными и противозадирными качествами.Материалы червячных пар
Слайд 55 Витки червяка и зубчатый венец червячного
колеса должны обладать достаточной прочностью и составлять антифрикционную пару, обладающую
высокой износостойкостью и сопротивляемостью заеданию в условиях больших скоростей скольжения при значительных нормальных силах между контактирующими поверхностями.Для изготовления червяков применяют все три типа сталей, распространенных в машиностроении:
Слайд 561. качественные среднеуглеродистые стали марок 40, 45, 50.
Из них изготавливают малоответственные червяки. Заготовку перед механической обработкой подвергают
улучшающей термической обработке (HRC ≤ 36). Червяк точат на токарном станке с последующей ручной или механической шлифовкой и полировкой рабочих поверхностей витков.
Слайд 572. Среднеуглеродистые легированные стали марок 40Х, 45Х, 40ХН,
40ХНМА, 35ХГСА. Из этих сталей изготавливают червяки ответственных передач. Улучшающей
термообработке (HRCэ ≤ 45) подвергают деталь после предварительной обработки на токарном станке. После термообработки рабочие поверхности витков шлифуют на специальных червячно-шлифовальных станках или на токарном станке с применением специальной шлифовальной головки.
Слайд 583. Мало- и среднеуглеродистые легированные стали марок 20Х,
12ХН3А, 25ХГТ, 38ХМЮА. Из этих сталей изготавливают червяки высоконагруженных передач,
работающие в реверсивном режиме. Деталь, изготовленная с минимальным припуском под окончательную обработку, подвергается поверхностной химико-термической обработке (цементация, азотирование и т.п.) глубиной до 0,8 мм, после чего закаливается до высокой поверхностной твердости (HRCэ 55…65). Рабочая поверхность витков червяка шлифуется и полируется (иногда шевингуется).
Слайд 59Материалы, применяемые для изготовления червяков
Примечание: Термообработку улучшение с твердостью 350
HB применяют для передач малой мощности (до 1 кВт) и
непродолжительной работы.
Слайд 60 Материалы зубчатых венцов червячных колес по мере
убывания антизадирных и антифрикционных свойств и рекомендуемыми скоростями скольжения можно
подразделить на три группы:
Слайд 611 группа - оловянные бронзы.
Применяют при скорости скольжения Vs
5 м/с
2 группа - безоловянные бронзы и латуни.
Применяют при скорости скольжения 2 м/с Vs 5 м/с3 группа – мягкие серые чугуны.
Применяют при скорости скольжения Vs 2 м/с
и в ручных приводах.
Слайд 62 Зубчатые венцы червячных колёс изготавливают чаще
всего литьём из бронзы или чугуна. Чугунный венец (серые чугуны
СЧ15, СЧ20 или ковкие чугуны КЧ15, КЧ20) может отливаться за одно целое с ободом червячного колеса при отливке последнего. Такие колеса применяются, как правило, в низкоскоростных открытых и закрытых передачах (vs ≤ 2 м/с).
Слайд 63 При средних скоростях скольжения (2 < vs
≤ 5 м/с) для изготовления зубчатых венцов червячных колес применяются
безоловянистые бронзы и латуни.Чаще всего для этой цели используются железоалюминиевые литейные бронзы (Бр А9Ж3Л,
Бр А10Ж4Н4Л). Эти бронзы имеют высокую механическую прочность, но обладает пониженными антизадирными свойствами, поэтому её применяют в паре с червяками, имеющими шлифованную и полированную рабочую поверхность витков высокой твердости (HRC ≥ 45).
Слайд 64 В передачах с высокой скоростью скольжения
(5 < vs ≤ 25 м/с) зубчатые венцы червячных колёс
изготавливают из оловянистых бронз (Бр О10Ф1,Бр О10Н1Ф1). Эти бронзы обладают пониженной прочностью по сравнению с безоловянистыми, но обладают хорошими антизадирными свойствами.
Слайд 67 Бронзовые венцы червячных колёс обычно изготавливают
отливкой в землю, в кокиль (металлическую форму) или центробежным литьём.
При этом отливки, полученные центробежным литьём, имеют наилучшие прочностные характеристики.
Слайд 68
Цветные металлы дороги и поэтому из
бронзы выполняется лишь зубчатый венец, который крепится на сравнительно дешёвой
стальной ступице.
Слайд 70 Заготовка для зубчатого венца может быть отлита
непосредственно на ободе червячного колеса, либо отливаться в виде отдельной
детали, тогда венец выполняется насадным с закреплением его как от возможности проворота, так и от продольного смещения.Конструкции червячных колес
Слайд 73ПОСАДКА С НАТЯГОМ
Крепление венца к ступице должно
обеспечивать фиксацию как от проворота (осевая сила червяка = окружной
силе колеса), так и от осевого "снятия" венца (окружная сила червяка = осевой силе колеса).
Слайд 74 Размеры и долговечность червячной передачи определяются
механическими антифрикционными свойствами материала колеса, т.к. в передаче со стальным
червяком колесо является наименее прочным элементом пары.
Слайд 75 При чрезмерных кратковременных перегрузках могут возникнуть пластические
деформации или хрупкое разрушение поверхностей зубьев колеса, вызванные повышенными контактными
напряжениями, и пластическая деформация или поломка зубьев, вызванные повышенными напряжениями изгиба.
Слайд 76 Исходя из вышесказанного, в передачах с
машинным приводом колесо рассчитывают:
На выносливость зубьев по контактным напряжениям.
На выносливость
зубьев по напряжениям изгиба.На контактную прочность при кратковременных перегрузках.
На прочность зубьев по напряжениям изгиба при кратковременных перегрузках.
.
Слайд 77 Считается, что расчет на выносливость зубьев по
контактным напряжениям предотвращает не только усталостное выкрашивание рабочих поверхностей, но
также и заедание.
Слайд 79 В основу расчета положена формула Г.Герца
для определения максимальных контактных напряжений при линейном контакте
