Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логические задачи. Виды логических задач
Содержание
- 1. Логические задачи. Виды логических задач
- 2. Из истории логики
- 3. Аристотель и его вклад в развитие логикитерминология логикитеория умозаключений и доказательствосновные законы мышлениялогические операции
- 4. Развитие логики в XVIII-XIX векахГотфрид Вильгельм Лейбниц (1646 - 1716)Джордж Буль (1815—1864)
- 5. Вклад в развитие логики русских ученыхПорецкий Платон Сергеевич (1846-1907)Жегалкин Иван Иванович (1869-1947)
- 6. Логика: XX векДавид Гильберт (1862-1943)С.К. КлиниА. ЧёрчА.А МарковП.С. Новиков
- 7. Виды логических задачИстинноностные задачиЗадачи на пересечение и
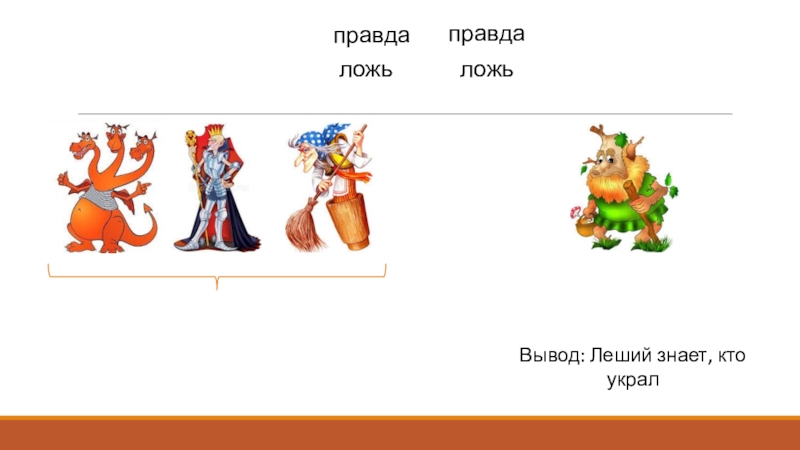
- 8. Истинноностные задачиЗадача 1. Украли у Ивана Царевича
- 9. ложьложьправдаправдаВывод: Леший знает, кто украл
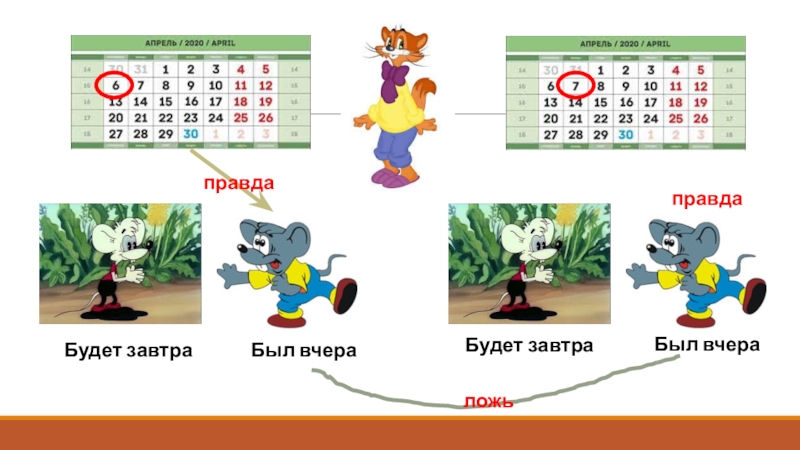
- 10. Истинноностные задачиЗадача 2.Каждый день кот Леопольд прогуливался
- 11. Был вчераБыл вчераБудет завтраБудет завтраправдаложьправда
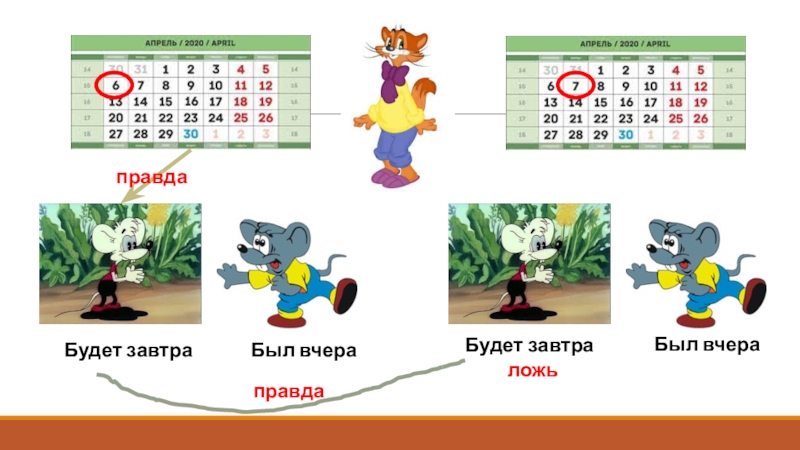
- 12. Был вчераБыл вчераБудет завтраБудет завтраправдаложьправда
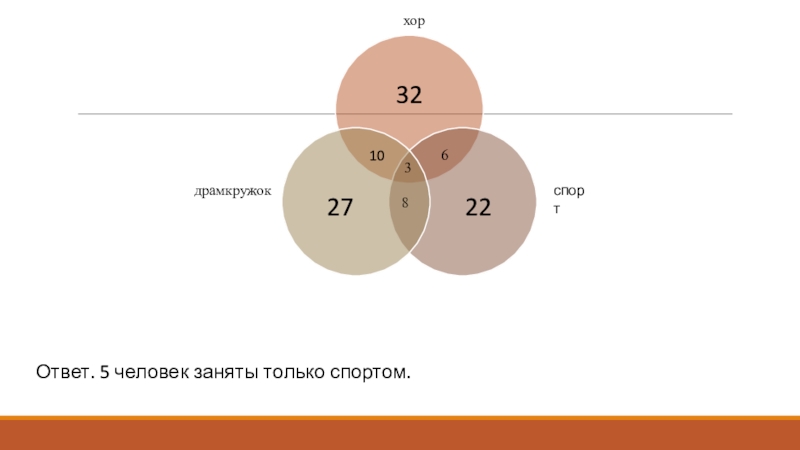
- 13. Задачи на пересечение и объединение множествЗадача 3.В
- 14. Ответ. 5 человек заняты только спортом.хордрамкружокспорт10863
- 15. Задачи на пересечение и объединение множествЗадача 4.Из
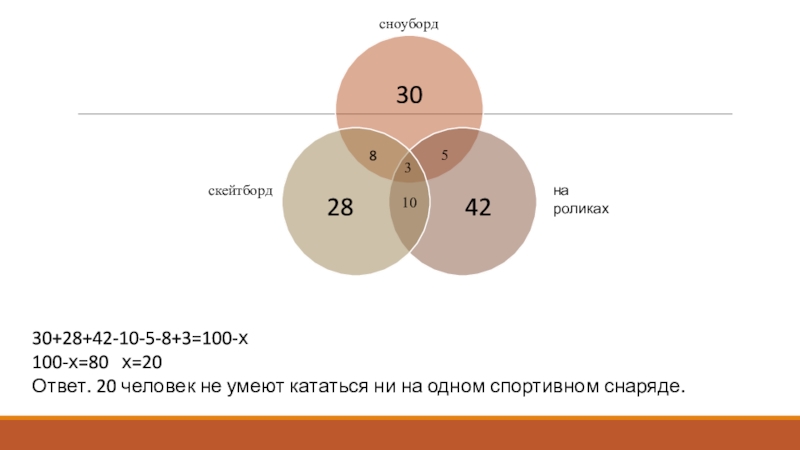
- 16. 30+28+42-10-5-8+3=100-х100-х=80 х=20Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде.сноубордскейтбордна роликах81053
- 17. Задачи на переливаниеЗадача 5. Тому Сойеру нужно
- 18. Задачи на переливаниеРешение:
- 19. Задачи на переливаниеЗадача 6. Однажды Винни-Пух захотел
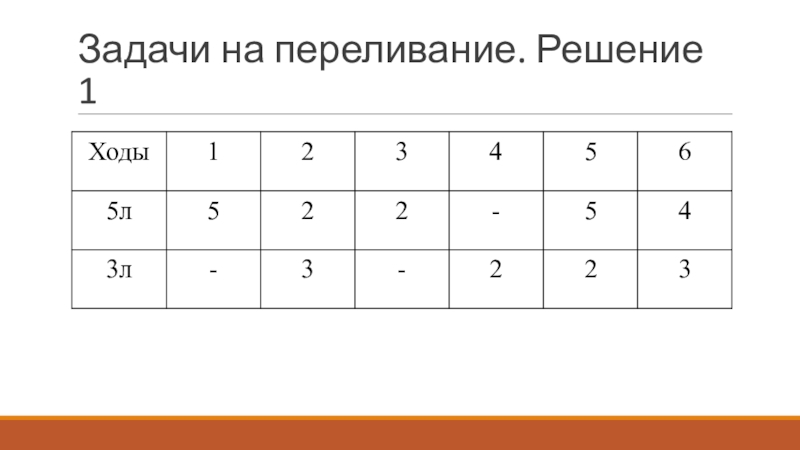
- 20. Задачи на переливание. Решение 1
- 21. Задачи на переливание. Решение 2
- 22. Задачи на взвешиваниеЗадача 7. Среди 101 одинаковых
- 23. Задачи на взвешивание: взвешиваем 50 и 50
- 24. Задачи на взвешиваниеЗадача 8. На рисунках А
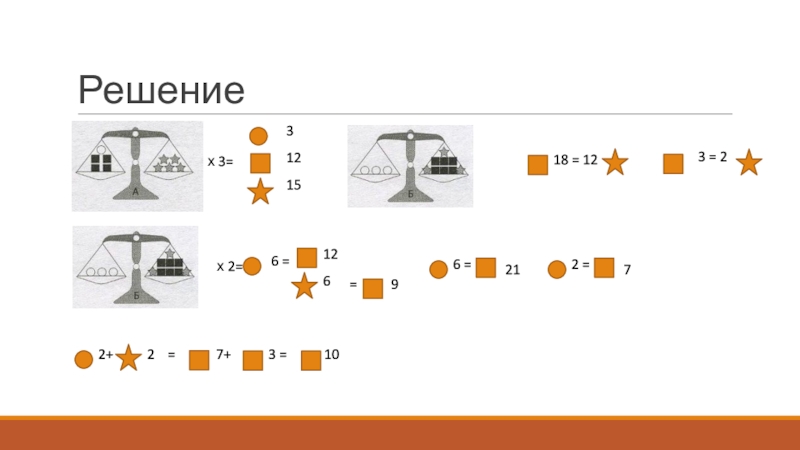
- 25. Решениех 3=6 = 1263 = 2х 2==
- 26. Задачи, решаемые с концаЗадача 9. Трое мальчиков
- 27. Задачи, решаемые с конца
- 28. Задачи, решаемые с концаЗадача 10. Однажды черт
- 29. Решение
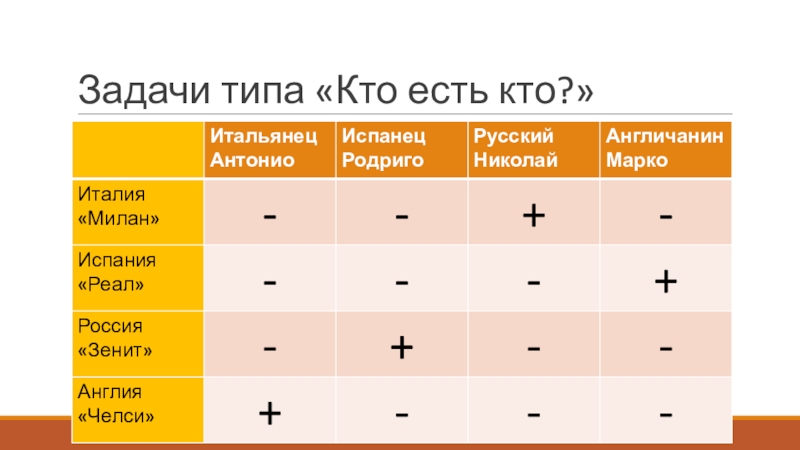
- 30. Задачи типа «Кто есть кто?»Задача 11.
- 31. Задачи типа «Кто есть кто?»
- 32. Электронный ресурсhttp://kvant-matematika.tilda.ws/
- 33. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Аристотель и его вклад в развитие логики
терминология логики
теория умозаключений и
доказательств
Слайд 4Развитие логики в XVIII-XIX веках
Готфрид Вильгельм Лейбниц (1646 - 1716)
Джордж
Буль (1815—1864)
Слайд 5Вклад в развитие логики русских ученых
Порецкий Платон Сергеевич (1846-1907)
Жегалкин Иван
Иванович (1869-1947)
Слайд 7Виды логических задач
Истинноностные задачи
Задачи на пересечение и объединение множеств
Задачи на
переливание
Задачи на взвешивание
Задачи, решаемые с конца
Задачи типа «Кто есть кто?»
(перебор вариантов)Слайд 8Истинноностные задачи
Задача 1. Украли у Ивана Царевича Василису Прекрасную. Поехал
он выручать ее. Поймал Змея Горыныча, Бабу Ягу, Кощея Бессмертного
и Лешего – Иван Царевич знал, что один из них украл ее. И спрашивает: «Кто украл Василису?» Змей Горыныч, Баба Яга и Кощей Бессмертный ответили: «Не я», а Леший – «Не знаю». Потом оказалось, что двое из них сказали правду, а двое – неправду. Знает ли Леший, кто украл Василису?Слайд 10Истинноностные задачи
Задача 2.
Каждый день кот Леопольд прогуливался в городском парке.
Однажды, 6 апреля кот Леопольд встретил на прогулке мышей –
Серого и Белого. Леопольд забыл, когда у мышат Дни Рождения и решил спросить их об этом, чтобы вовремя подарить подарки. «Он был вчера» - ответил Серый мышонок. Белый же мышонок сказал: «Он будет завтра». На следующий день кот Леопольд опять спросил мышат об этом. «Он был вчера» - ответил Серый мышонок. «Он будет завтра» - сказал Белый. Кот Леопольд задумался над словами мышат. Он точно знал, что обманывать они могут только в день своего рождения, хоть и часто шутят над ним. Как же коту Леопольду узнать, когда дни рождения у мышат?Слайд 13Задачи на пересечение и объединение множеств
Задача 3.
В пионерском лагере 70
ребят. Из них 27 занимаются в драмкружке, 32 поют в
хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?Слайд 15Задачи на пересечение и объединение множеств
Задача 4.
Из 100 ребят, отправляющихся
в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят,
на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?Слайд 1630+28+42-10-5-8+3=100-х
100-х=80 х=20
Ответ. 20 человек не умеют кататься ни на одном спортивном
снаряде.
сноуборд
скейтборд
на роликах
8
10
5
3
Слайд 17Задачи на переливание
Задача 5. Тому Сойеру нужно покрасить забор. Он
имеет 12 л краски и хочет отлить из этого количества
половину, но у него нет сосуда вместимостью в 6 л. У него 2 сосуда: один – вместимостью в 8 л, а другой – вместимостью в 5 л. Каким образом налить 6 л краски в сосуд на 8 л? Какое наименьшее число переливаний необходимо при этом сделать?12 л.
8 л.
5 л.
6 л. - ?
Слайд 19Задачи на переливание
Задача 6. Однажды Винни-Пух захотел полакомиться медом и
пошел к пчелам в гости. По дороге нарвал букет цветов,
чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л!» Винни-Пух долго думал, но все-таки смог решить задачку. Как он это сделал?5 л.
3 л.
4 л. - ?
Слайд 22Задачи на взвешивание
Задача 7. Среди 101 одинаковых по виду монет
одна фальшивая, отличающаяся по весу. Как с помощью чашечных весов
без гирь за два взвешивания определить, легче или тяжелее фальшивая монета? Hаходить фальшивую монету не требуется.Слайд 23Задачи на взвешивание: взвешиваем 50 и 50 монет
1 случай
Равенство. Берем
оставшуюся монету и ставим ее в левую кучку вместо одной
из имеющихся там:а) Левая кучка тяжелее => фальшивая монета тяжелее;
б) Левая кучка легче => фальшивая монета легче.
2 случай
Неравенство. Берем более тяжелую кучку и разбиваем ее на две кучки по 25 монет:
а) Вес кучек одинаковый => фальшивая монета легче;
б) Вес кучек неодинаковый => фальшивая монета тяжелее.
Слайд 24Задачи на взвешивание
Задача 8. На рисунках А и Б чашечные
весы находятся в равновесии. Как вы думаете, сколько кубических гирек
(на рисунке изображены в виде квадрата) надо использовать, чтобы уравновесить весы В?Слайд 26Задачи, решаемые с конца
Задача 9. Трое мальчиков имеют по некоторому
количеству яблок. Первый мальчик дает другим столько яблок, сколько каждый
из них имеет. Затем второй мальчик дает двум другим столько яблок, сколько каждый из них теперь имеет; в свою очередь и третий дает каждому из двух других столько, сколько есть у каждого в этот момент. После этого у каждого из мальчиков оказывается по 8 яблок. Сколько яблок было у каждого мальчика в начале?Слайд 28Задачи, решаемые с конца
Задача 10. Однажды черт предложил бездельнику заработать.
“Как только ты перейдешь через этот мост, – сказал он,
– твои деньги удвоятся. Можешь переходить по нему сколько хочешь раз, но после каждого перехода отдавай мне за это 24 рубля”. Бездельник согласился и … после третьего перехода остался без денег. Сколько денег у него было сначала?Слайд 30Задачи типа «Кто есть кто?»
Задача 11. Четыре футбольных команды:
итальянская команда «Милан», испанская – «Реал», российская – «Зенит», английская
– «Челси» встретились в групповом этапе лиги чемпионов по футболу. Их тренировали тренеры из этих же четырех стран: итальянец Антонио, испанец Родриго, русский Николай, англичанин Марк. Известно, что национальность у всех четырех тренеров не совпадала с национальностью команд. Требуется определить тренера каждой команды, если известно:а) Зенит не тренируется у Марка и Антонио.
б) Милан обещал никогда не брать Марка главным тренером.



























![Русская культура 16-17 веков.ppt [Автосохраненный]](/img/thumbs/0e74315048d55af1a7c6eba213b21ced-800x.jpg)















