Слайд 1Математическая статистика
Лекции по математике
Слайд 2И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Рекомендуемая литература
Кремер
Н.Ш. Теория вероятностей и математическая статистика. - М.: Банки и
биржи, ЮНИТИ, 2001 .
Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: В.Ш., 2002 .
Кропачева Н.Ю., Петросян Г.А. Элементы математической статистики. Учебное пособие по изучению курса высшей математики. – СПб.: Изд-во СПбГАСЭ, 2004. – 79 с.
Тимошина И.Р. Электронный конспект лекций по математической статистике. ВФ СПбГУСЭ, 2007.
Слайд 3И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Содержание
Средние характеристики
вариационного ряда
Показатели вариации
Статистические оценки числовых характеристик и параметров распределения
Анализ смещённости
выборочной средней и выборочной дисперсии
Слайд 4И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Числовые характеристики
вариационного ряда
Вариационный ряд содержит достаточно полную информацию об изменчивости признака.
Однако обилие числовых данных иногда затрудняет практическое использование этой информации.
На практике часто достаточно использовать некоторые числовые характеристики: средние характеристики; характеристики изменчивости и т.д.
Слайд 5И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Средние характеристики
вариационного ряда
Пусть проведена выборка объёмом n.
Выборочной средней арифметической
вариационного ряда называется среднее арифметическое значений выборки.
Если все варианты x1, x2,… xn различны, то
Слайд 6И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Средние характеристики
вариационного ряда
Если же варианты x1, x2,… xk имеют соответственно частоты
n1, n2,… nk , то
Из определения следует, что ,
где w1, w2,… wk - относительные частоты вариант.
Слайд 7И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Средние характеристики
вариационного ряда
Для интервального ряда в этой же формуле
в качестве
значения xi следует выбирать середину соответствующего интервала.
Слайд 8И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Средние характеристики
вариационного ряда
В некоторых случаях выборочные значения случайной величины целесообразно разбивать
на отдельные группы. В каждой группе можно найти её среднюю.
Групповой средней называют среднее арифметическое значений выборки, принадлежащих группе.
Слайд 9И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Средние характеристики
вариационного ряда
По этим групповым средним можно найти среднее для всей
выборки.
Общей средней называют среднее арифметическое значение групповых средних.
Слайд 10И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Пример. Найти
общую среднюю на основе
выборки:
Решение. Находим групповые средние:
Общая средняя:
Слайд 11И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Средние характеристики
вариационного ряда
Начальным эмпирическим моментом порядка k называется величина
Начальный эмпирический момент
первого порядка равен выборочной средней.
Слайд 12И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Средние характеристики
вариационного ряда
Центральным эмпирическим моментом порядка k называется величина
Слайд 13И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Средние характеристики
вариационного ряда
Медианой (Ме) называют варианту, которая делит вариационный ряд на
две равные части.
Для дискретного ряда:
при четном числе вариант -
при нечетном числе вариант - ,
где xm и xm+1 - средние значения вариант.
Слайд 14И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Пример. Найти
медиану для рядов:
а) 2 3 5 6 7;
б) 2 3 5 6 7 9.
Решение. В случае а) медиана равна 5.
В случае б) медиана равна (5+6)/2=5,5.
Слайд 15И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Средние характеристики
вариационного ряда
Модой (Мo) называют варианту, которая имеет наибольшую частоту.
Особенностями
медианы и моды, как мер центральной тенденции, является то, что они устойчивы к вариации признаков.
Слайд 16И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Пример. Найти
моду вариационного ряда:
Решение. Мода равна 7, так как частота
этой
варианты наибольшая.
Слайд 17И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
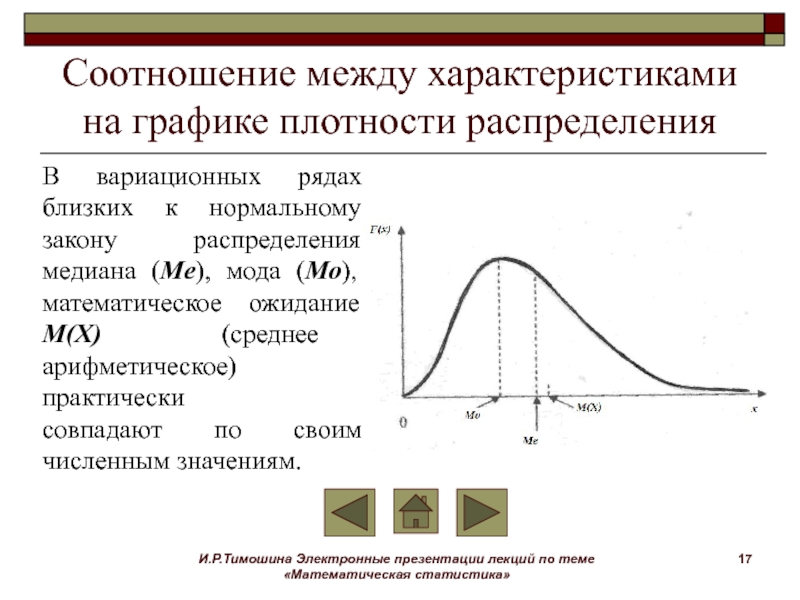
Соотношение между
характеристиками на графике плотности распределения
В вариационных рядах близких к нормальному
закону распределения медиана (Мe), мода (Мо), математическое ожидание М(X) (среднее арифметическое) практически
совпадают по своим численным значениям.
Слайд 18И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Показатели вариации
Выборочной
дисперсией называется среднее арифметическое квадратов отклонений наблюдаемых
значений от выборочного среднего.
Если все значения выборки различны, то
Слайд 19И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Показатели вариации
Если
значения выборки имеют соответствующие частоты, то
Выборочным средним квадратическим отклонением
называется квадратный корень из выборочной дисперсии:
Слайд 20И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Показатели вариации
Размахом
варьирования называют разность
Коэффициентом вариации называют величину
Слайд 21И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Асимметрия и
эксцесс
Асимметрия:
Эксцесс:
Слайд 22И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Статистические оценки
параметров распределения
Пусть требуется изучить количественный признак генеральной совокупности, к примеру,
скорость молекул газа при заданной температуре. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет этот признак. Возникает задача оценки параметров этого распределения. Например, если известно, что исследуемый признак имеет нормальное распределение, то необходимо оценить математическое ожидание и среднее квадратическое отклонение.
Слайд 23И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Статистические оценки
параметров распределения
Обычно в распоряжении исследователя имеются лишь данные выборки x1,
x2,… xn, полученные в результате наблюдений. Введём случайные величины: X1, X2,… Xn - случайные величины, где Xi – результат i-го наблюдения. Будем считать, что X1, X2,… Xn - независимые случайные величины, а x1, x2,… xn - реализации этих величин, полученные в ходе экспериментов.
Слайд 24И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Статистические оценки
параметров распределения
Статистической оценкой неизвестного параметра распределения называется функция от наблюдаемых
случайных величин, которая позволяет вычислить приближённое значение этого параметра.
Слайд 25И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Статистические оценки
параметров распределения
Примером оценки математического ожидания случайной величины может служить среднее
арифметическое наблюдаемого значения признака:
Слайд 26И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Статистические оценки
параметров распределения
Обозначим θ∗ оценку некоторого теоретического параметра θ закона распределения
случайной величины X.
По определению, оценка – функция, зависящая от случайных величин X1, X2,…, Xn. Следовательно, оценка – тоже случайная величина. Важно, чтобы эта оценка не имела систематических ошибок, а её отклонения от оцениваемого параметра были как можно меньше.
Слайд 27И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Несмещённые, эффективные
и состоятельные оценки
Несмещённой называют статистическую оценку, математическое ожидание которой равно
оцениваемому параметру,
т.е.M (θ∗)= θ.
Смещённой называется оценка, математическое ожидание которой не равно оцениваемому параметру.
Слайд 28И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Несмещённые, эффективные
и состоятельные оценки
Эффективной называют оценку, которая при заданном объёме выборки
имеет наименьшую дисперсию.
Состоятельной называют статистическую оценку, которая при стремящемся к бесконечности n стремится по вероятности к оцениваемому параметру,
Слайд 29И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Анализ смещённости
выборочной средней и выборочной дисперсии
Теорема. Выборочное среднее
является несмещённой оценкой математического ожидания случайной величины X .
Доказательство. Пусть дана выборка x1, x2,… xn. Будем рассматривать выборочные значения как реализации случайных величин X1, X2,…, Xn, распределённых так же, как случайная величина X.
Слайд 30И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Анализ смещённости
выборочной средней и выборочной дисперсии
Это означает, что они имеют одно
и то же математическое ожидание Mx и дисперсию
Тогда , ч.т.д.
Слайд 31И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Анализ смещённости
выборочной средней и выборочной дисперсии
Теорема. Выборочная дисперсия является смещённой
оценкой дисперсии случайной величины X.
Доказательство.
т.е. оценка дисперсии является смещённой.
Слайд 32И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Анализ смещённости
выборочной средней и выборочной дисперсии
Чтобы «исправить» выборочную дисперсию, её нужно
умножить на дробь
В результате получим несмещённую оценку для выборочной дисперсии:
или для конкретной выборки
Слайд 33И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Пример. Статистическое
распределение
выборки случайной величины имеет вид:
Найти несмещённую оценку математического
ожидания, смещённую и несмещённую оценки
дисперсии.
Решение. Вычислим несмещённую оценку
математического ожидания:
Слайд 34И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Вычислим смещённую
оценку дисперсии:
Вычислим несмещённую оценку дисперсии: