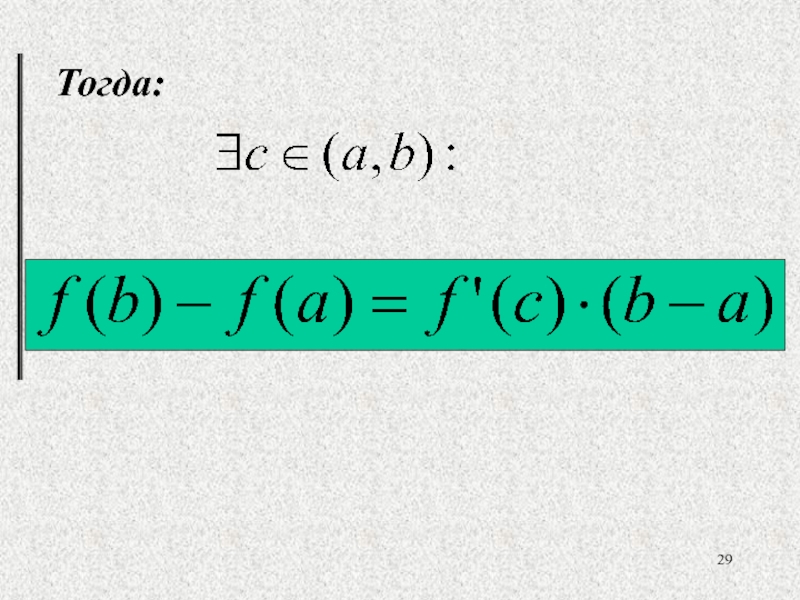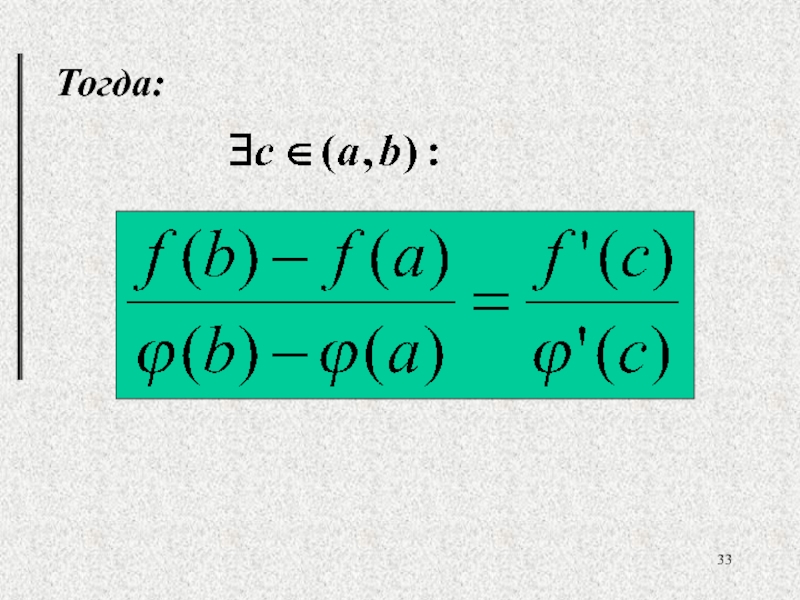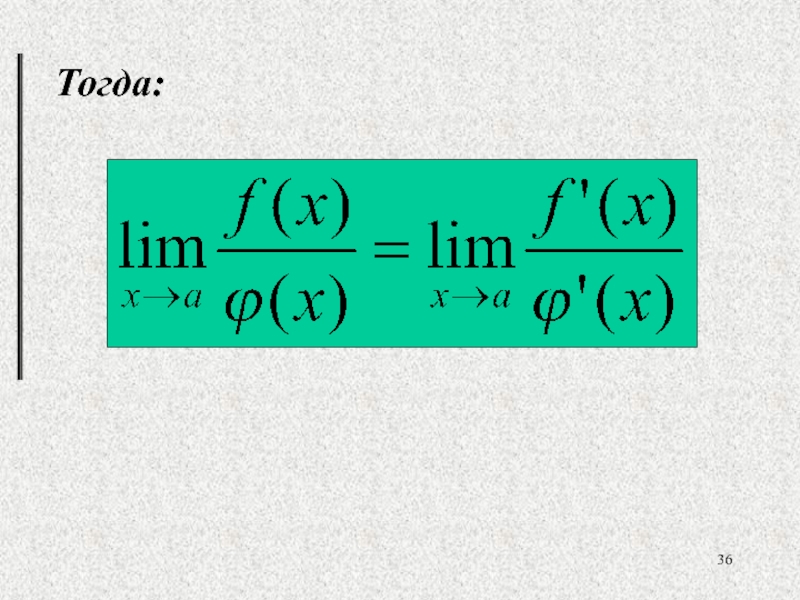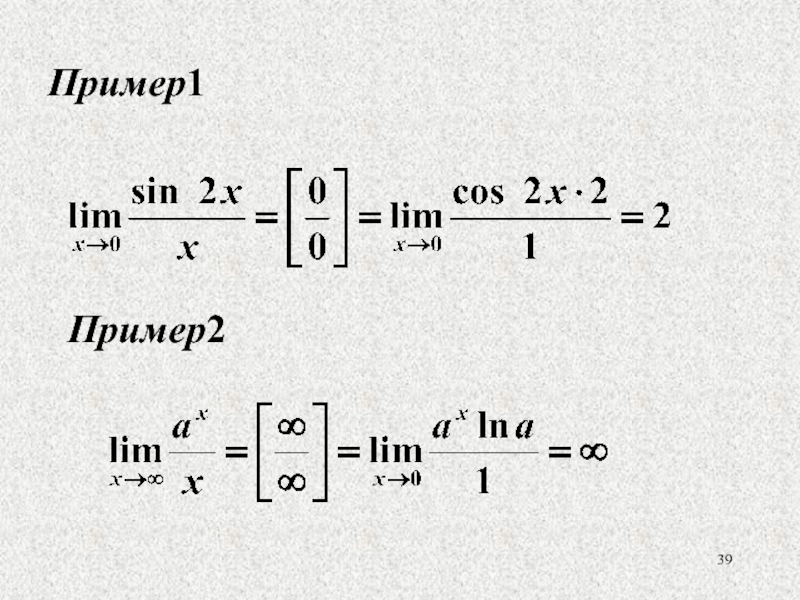Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика Часть 1
Содержание
- 1. Математика Часть 1
- 2. Лекция 113. Приближенное вычисление малых
- 3. Производной второго порядка от
- 4. Производной -го порядка называется производная первого
- 5. Правила вычисления производной -го порядка
- 6. Вторая производная от неявной функции
- 7. Вторая производная от параметрическизаданной функции
- 8. Механический смысл второй производной
- 9. Дифференциал функции
- 10. Обозначение: *)
- 11. Слайд 11
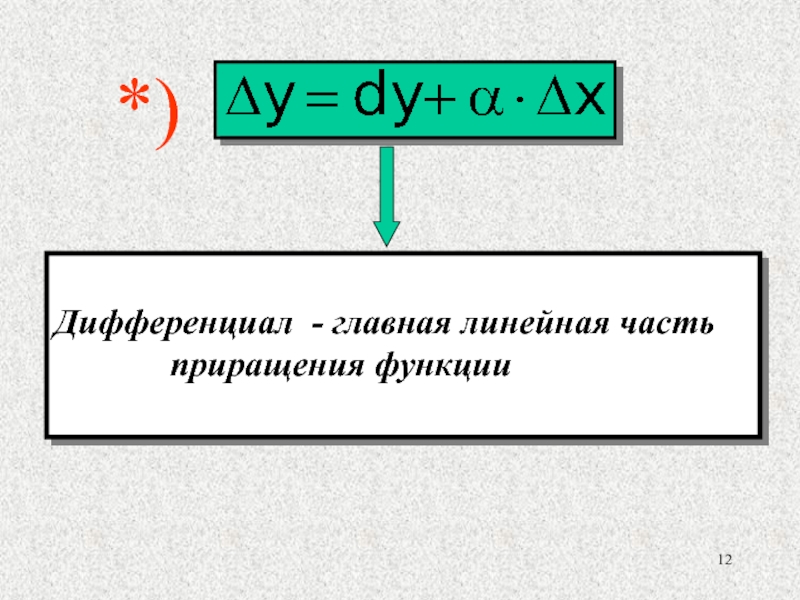
- 12. Дифференциал - главная линейная часть
- 13. Дифференциал независимой переменной
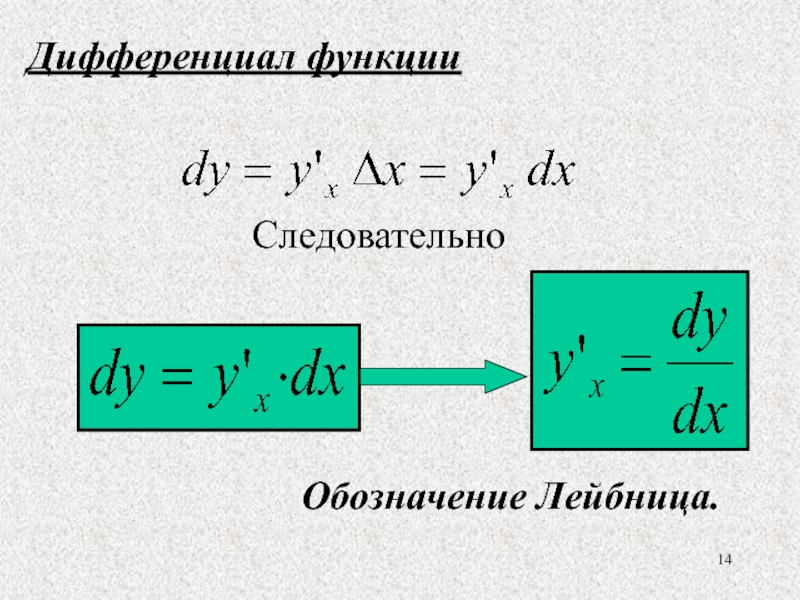
- 14. Дифференциал функции
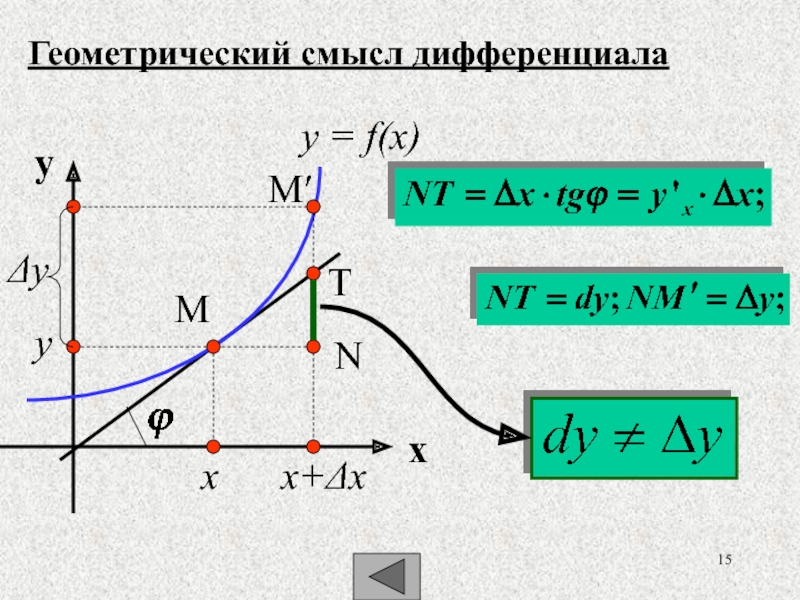
- 15. Геометрический смысл дифференциалаTy = f(x)xy y NMMx+x
- 16. Свойства дифференциалов
- 17. Приближенное вычисление малых приращений функции при помощи дифференциала.
- 18. Дифференциалы высших порядков.
- 19. Слайд 19
- 20. Формулы для дифференциалов высших порядковОкончательно
- 21. Слайд 21
- 22. Основные теоремы анализа.I. Теорема Ролля (о нуле производной)
- 23. Тогда:
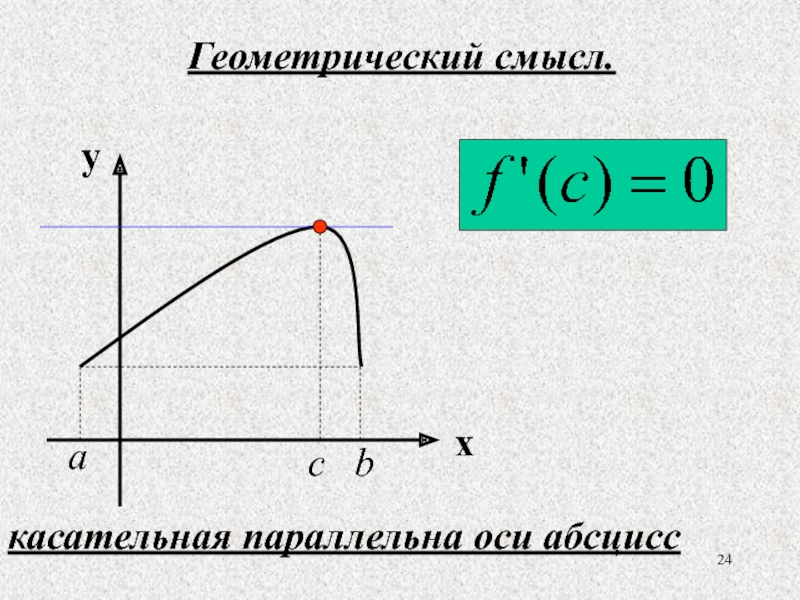
- 24. Геометрический смысл. a b c касательная параллельна оси абсцисс
- 25. Следствие. Теорема Ролля позволяет узнать об обращении производной в ноль без ее вычисления. Пример.Решение.Три отрезка:
- 26. На каждом выполнены условия теоремы Ролля Три
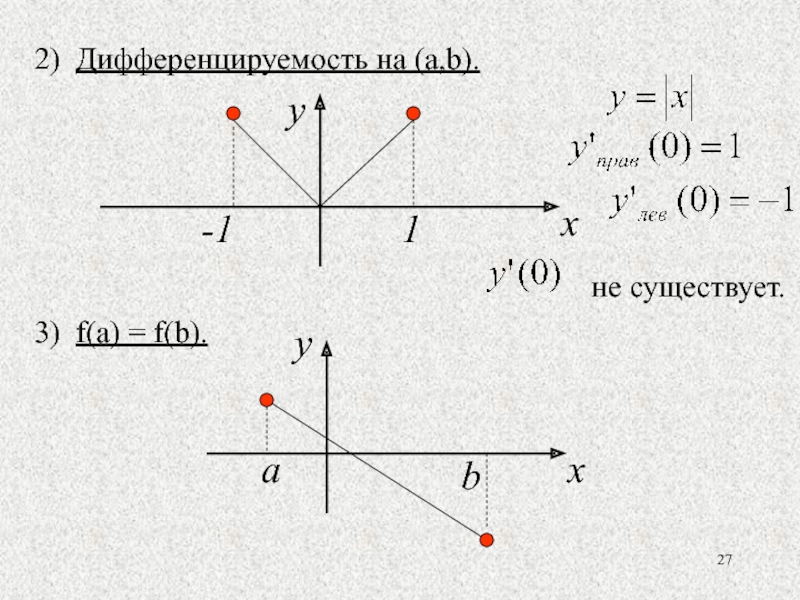
- 27. 2) Дифференцируемость на (a,b). 3) f(a) = f(b).
- 28. II. Теорема Лагранжа (формула конечныхприращений)
- 29. Тогда:
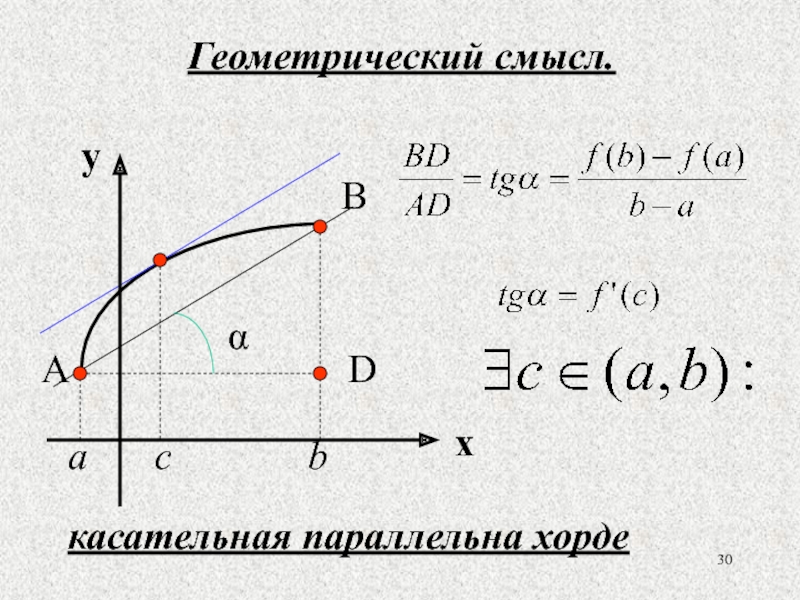
- 30. Геометрический смысл. касательная параллельна хорде
- 31. Замечания.1) Теорему Лагранжа можно использовать для приближенных вычислений значений функции. Можно записатьa b c
- 32. 2) Теорема Ролля является частным случаем теоремы Лагранжа.III. Теорема Коши.
- 33. Тогда:
- 34. Замечание.Если (x) = x, - формула Коши
- 35. IV. Правило Лопиталя
- 36. Тогда:
- 37. Смысл.Предел отношения бесконечно малых функций равен пределу отношения их производных, при условии существования последнего.
- 38. Замечания.3) Правило Лопиталя можно применять несколько раз
- 39. Слайд 39
- 40. Скачать презентанцию
Лекция 113. Приближенное вычисление малых приращений функции 4. Дифференциалы высших порядков5. Основные теоремы анализа 2. Дифференциал функции1. Производные высших порядков
Слайды и текст этой презентации
Слайд 2Лекция 11
3. Приближенное вычисление малых
приращений функции
4. Дифференциалы высших порядков
Производные высших порядковСлайд 3 Производной второго порядка от
функции
называется производная
от ее первой производной.Производные высших порядков
Обозначение:




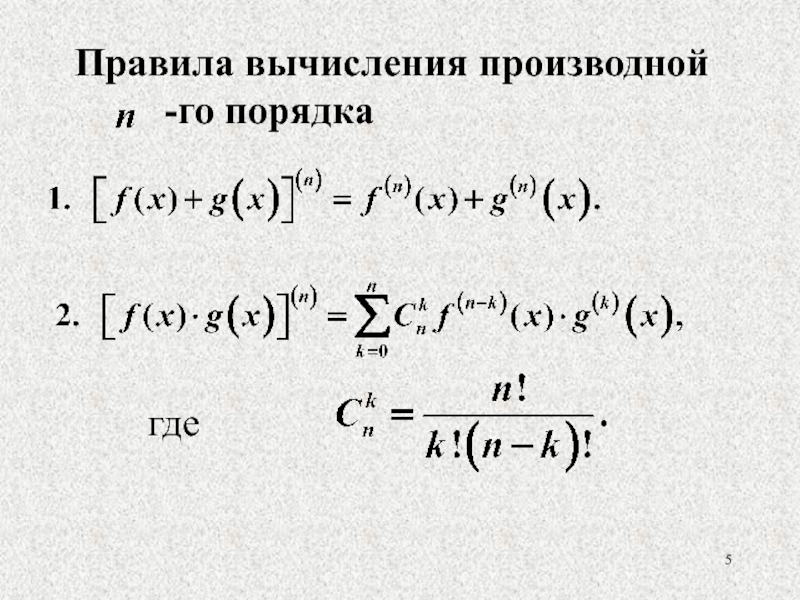







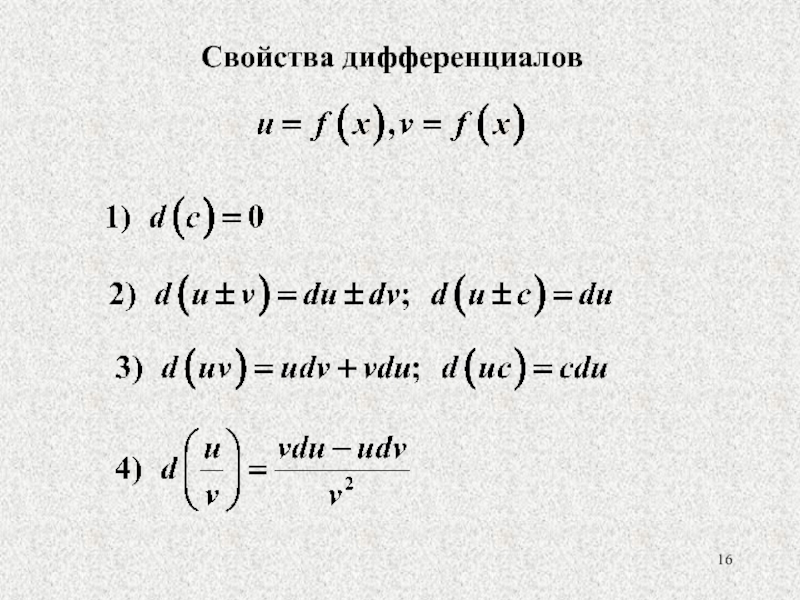


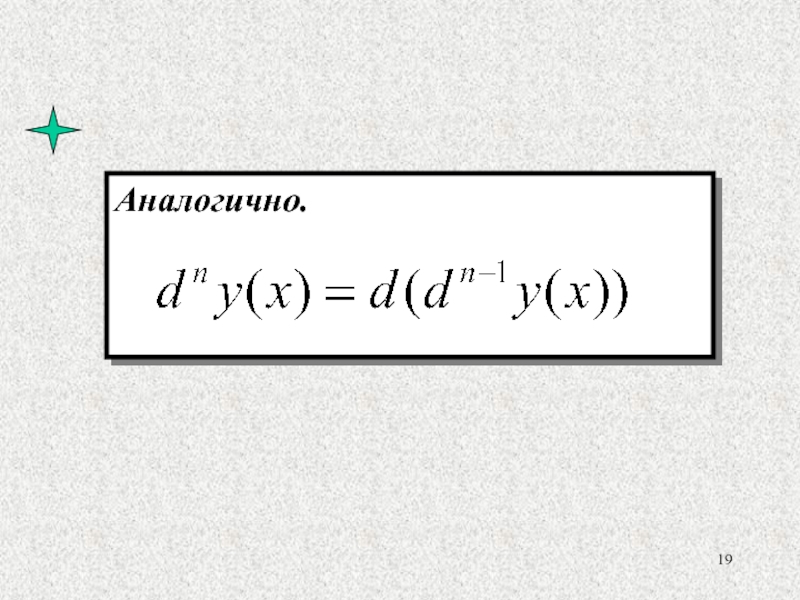

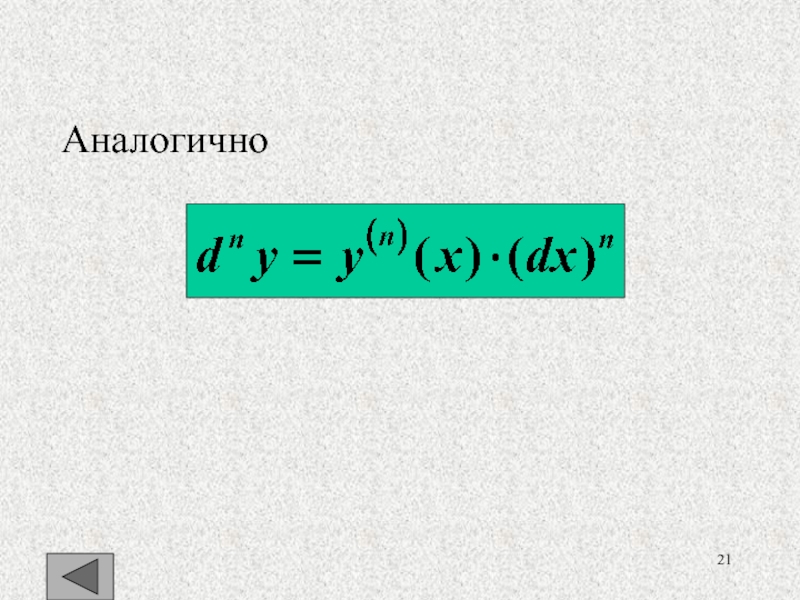

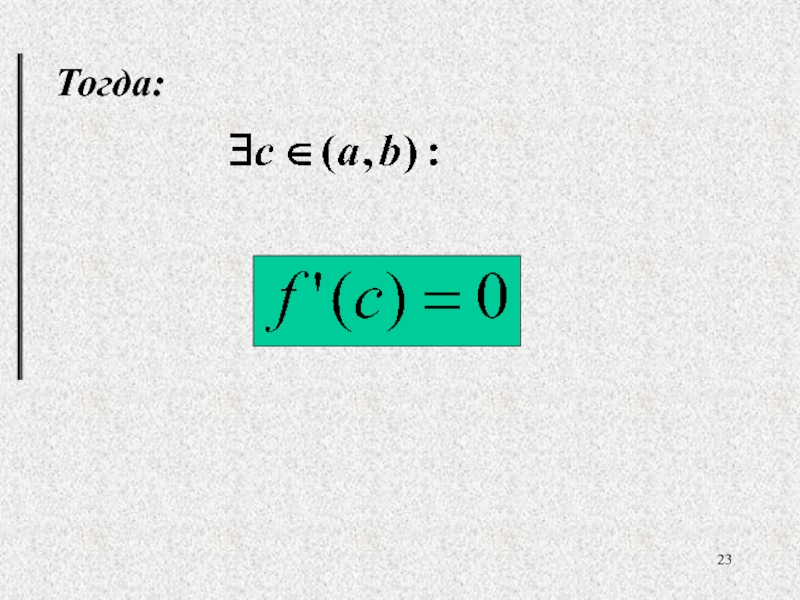

![Математика Часть 1 На каждом выполнены условия теоремы Ролля Три корня! Замечание.Все условия теоремы На каждом выполнены условия теоремы Ролля Три корня! Замечание.Все условия теоремы Ролля важны. 1) Непрерывность на [a,b].](/img/thumbs/67097622726ae215eb5bf4fed1190f9e-800x.jpg)