Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод электронного парамагнитного резонанса в исследованиях свойств биосистем
Содержание
- 1. Метод электронного парамагнитного резонанса в исследованиях свойств биосистем
- 2. Метод ЭПР является основным методом для изучения
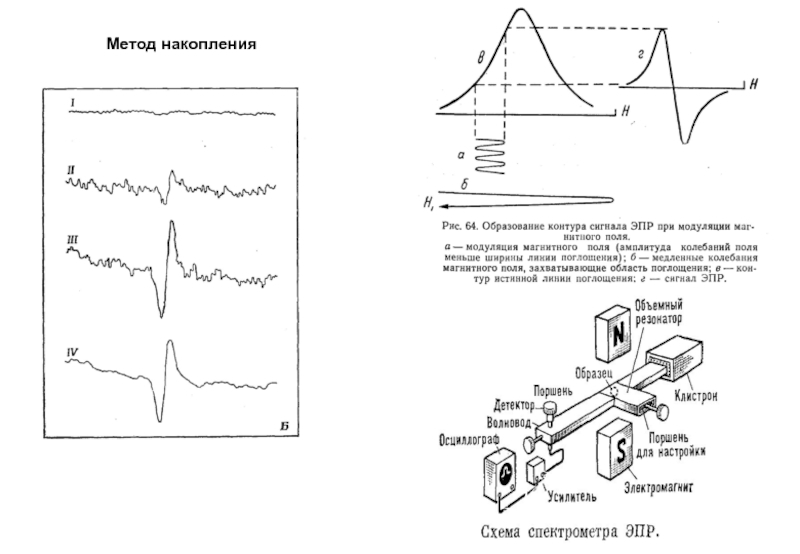
- 3. Метод накопления
- 4. Индукция магнитного поля лежит в диапазоне (0,34-1,25
- 5. Орбитальные механический и магнитный моменты электронаОрбитальный момент
- 6. Спиновые механический и магнитный моментыСпиновый магнитный момент
- 7. Магнетон Бора Для n=1 величина μ называется магнетоном
- 8. эффект ЗееманаРаспределение БольцманаПарамагнитные частицы могут обмениваться энергией
- 9. Характеристики спектров ЭПРАмплидута сигналаПлощадь под кривой поглощения
- 10. Тонкая структура спектров ЭПРСверхонкая структура спектров ЭПРВместо
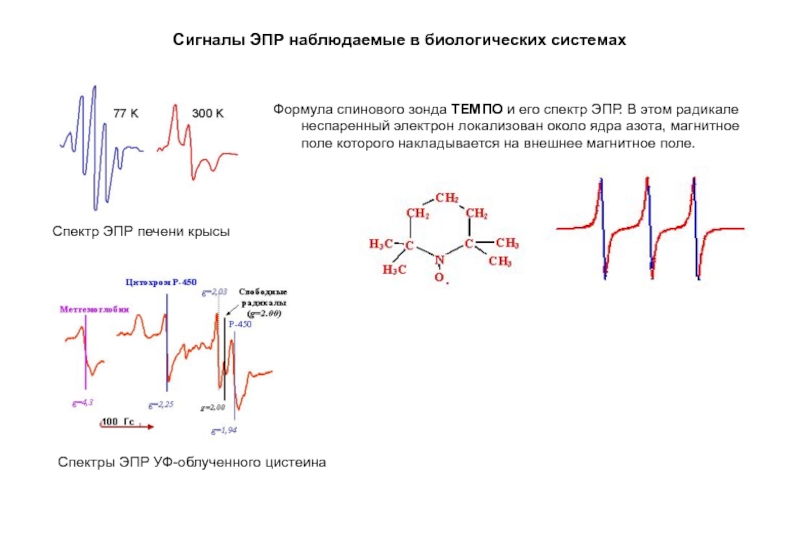
- 11. Сигналы ЭПР наблюдаемые в биологических системахСпектр ЭПР
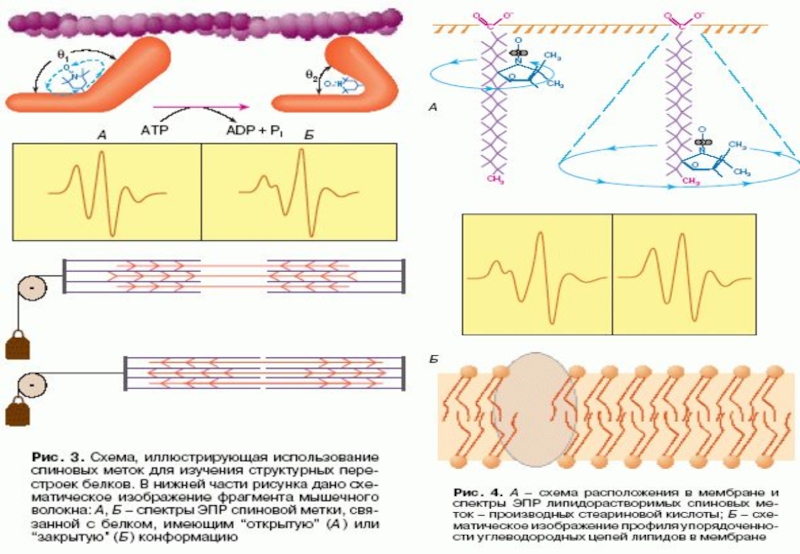
- 12. Слайд 12
- 13. Двойной электронно-ядерный резонанс (ДЭЯР) (самостоятельный разбор)___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
- 14. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Метод электронного парамагнитного резонанса в исследованиях свойств биосистем
Спектрометр ЭПР
ВИГТ.421400.012
на диоде Ганна.Слайд 2Метод ЭПР является основным методом для изучения парамагнитных частиц присутствующих
в биологических системах.
Метод ЭПР был открыт в 1944 г.
в Казанском Университете Евгением Константиновичем ЗАВОЙСКИМ при исследовании поглощения электромагнитной энергии парамагнитными солями металлов. Позволяет избирательно детектировать и изучать электронное строение различных парамагнитных частиц.
Современные спектрометры позволяют изучать парамагнитные молекулы непосредственно в процессе функционирования нативных биологических систем
Можно изучать даже небольших животных помещенных в специально сконструированный резонатор спектрометра
Позволяет обнаруживать неспаренные электроны при низкой их концентрации (10-5 М) в любом веществе, не разрушая и не видоизменяя его.
Методом ЭПР можно определять концентрацию и идентифицировать парамагнитные частицы в любом агрегатном состоянии, что незаменимо для исследования кинетики и механизма процессов, происходящих с их участием
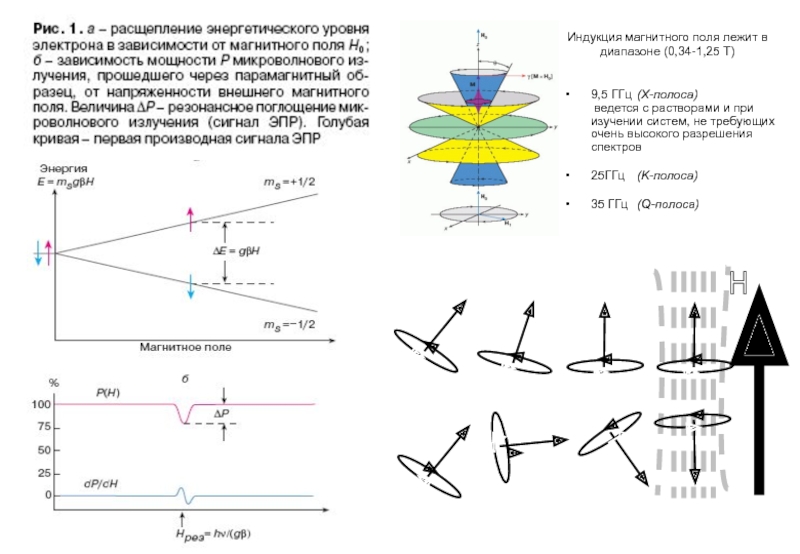
Слайд 4Индукция магнитного поля лежит в диапазоне (0,34-1,25 Т)
9,5 ГГц (X-полоса)
ведется с растворами и при изучении систем, не требующих очень
высокого разрешения спектров25ГГц (K-полоса)
35 ГГц (Q-полоса)
Слайд 5Орбитальные механический и магнитный моменты электрона
Орбитальный момент количества движения электрона
Р по орбите радиуса R равен (1) где m- масса электрона,
v - его скоростьОрбитальному механическому моменту соответствует орбитальный магнитный момент (2) где I - сила тока в контуре, а S - площадь контура
С другой стороны, из атомной физики известно, что орбитальный механический момент выражается через орбитальное квантовое число следующим образом (3)
n - орбитальное квантовое число, принимающее значения 0, 1, 2 и т.д
Тогда магнитный орбитальный момент будет выглядеть
(4)
S = πR2
где e - заряд электрона
Слайд 6Спиновые механический и магнитный моменты
Спиновый магнитный момент электрона связан со
спиновым движением электрона, которое можно представить, как движение вокруг собственной
оси. Спиновый механический момент электрона равен где S - спиновое квантовое число равное ½Магнитный и механический спиновые моменты связаны соотношением где MS - магнитное квантовое число равное +1/2
В большинстве случаев орбитальный магнитный момент равен нулю (L=0)
поэтому при обсуждении принципа метода ЭПР рассматривается только спиновый магнитный момент
Слайд 7Магнетон Бора
Для n=1 величина μ называется магнетоном Бора и является
единичным магнитным моментом.
Эта величина равна 9,27*10-21 Дж/м*Тл (5)
Гиромагнитное отношение (γ)
Отношение
магнитного момента к механическому называется гиромагнитным отношением (g)
Для орбитального
Для спинового
g - фактор
Для гиромагнитного отношения электронов, имеющих различный вклад орбитального и спинового движения, вводят коэффициент пропорциональности g, такой, что
Этот коэффициент пропорциональности называется g-фактором.
когда отсутствует спиновое движение электрона и существует только орбитальное g=1 (S=0)
если отсутствует орбитальное движение и существует только спиновое (например, для свободного электрона)
g=2 (L=0)
Формула Ланде
1 < g < 2
Если свободный атом содержит несколько электронов, то их орбитальные и спиновые моменты складываются
В этом случае магнитные свойства атома будут определяться значениями квантовых чисел
L (суммарный орбитальный момент) и S (суммарный спиновый момент), а также полным квантовым числом J.
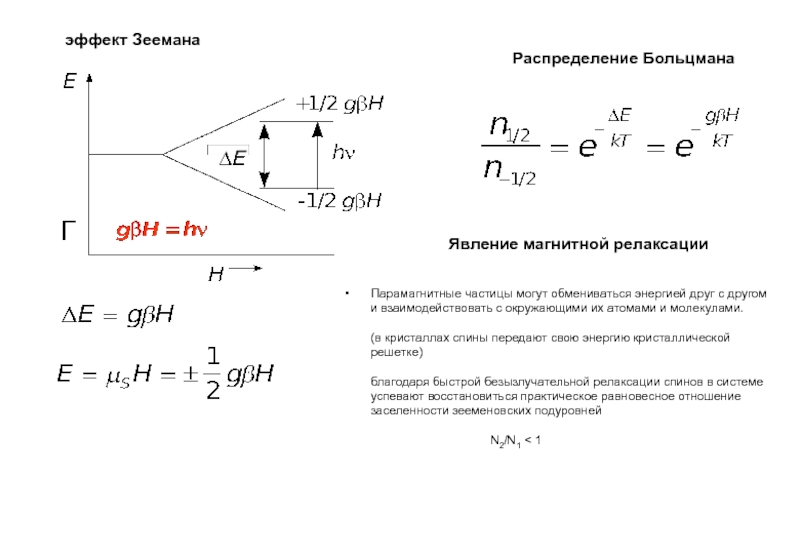
Слайд 8эффект Зеемана
Распределение Больцмана
Парамагнитные частицы могут обмениваться энергией друг с другом
и взаимодействовать с окружающими их атомами и молекулами. (в кристаллах спины
передают свою энергию кристаллической решетке) благодаря быстрой безызлучательной релаксации спинов в системе успевают восстановиться практическое равновесное отношение заселенности зееменовских подуровней N2/N1 < 1Явление магнитной релаксации
Слайд 9Характеристики спектров ЭПР
Амплидута сигнала
Площадь под кривой поглощения пропорциональна, при прочих
равных условиях, количеству парамагнитных частиц в образце
Общепринятым стандартом для таких
измерений является
дифенил-пикрилгидразил
(C6H5)2N-N-C6H5(NO2)3, который на 100% состоит из радикалов (неспаренных электронов на 1 г вещества)Форма линии
Функция Лоренца
Ширина спектра ЭПР зависит от взаимодействия магнитного момента электрона с магнитными моментами окружающих ядер (решетки) и электронов
Механизм релаксации заключается в передаче кванта электромагнитной энергии решетке или окружающим электронам и возвращении электрона на низкоэнергетический уровень
Позволяет судить о реальных взаимодействиях, которые испытывает неспаренный электрон и которые приводят к неизбежному «размазыванию» его энергии.
Ширина линии
Величина Т1 называется временем спин-решеточной релаксации (взаимодействия магнитного момента неспаренного электрона с решеткой ) и характеризует среднее время жизни спинового состояния
Величина Т2 называется временем спин-спиновой релаксации (взаимодействия магнитного момента неспаренного электрона с магнитными моментами других электронов)
Это взаимодействие приводит к уменьшению времени релаксации и тем самым к уширению линии спектра ЭПР
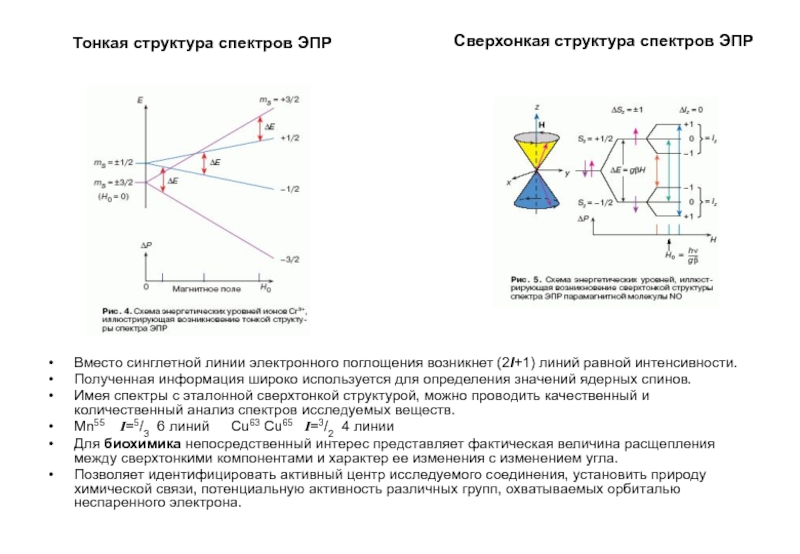
Слайд 10Тонкая структура спектров ЭПР
Сверхонкая структура спектров ЭПР
Вместо синглетной линии электронного
поглощения возникнет (2I+1) линий равной интенсивности.
Полученная информация широко используется для
определения значений ядерных спинов.Имея спектры с эталонной сверхтонкой структурой, можно проводить качественный и количественный анализ спектров исследуемых веществ.
Mn55 I=5/3 6 линий Cu63 Cu65 I=3/2 4 линии
Для биохимика непосредственный интерес представляет фактическая величина расщепления между сверхтонкими компонентами и характер ее изменения с изменением угла.
Позволяет идентифицировать активный центр исследуемого соединения, установить природу химической связи, потенциальную активность различных групп, охватываемых орбиталью неспаренного электрона.