Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод параллельного проектирования. Изображение пространственных фигур на
Содержание
- 1. Метод параллельного проектирования. Изображение пространственных фигур на
- 2. Итак, мы приступили к изучению стереометрии –
- 3. АВыберем в пространстве произвольную плоскость (её
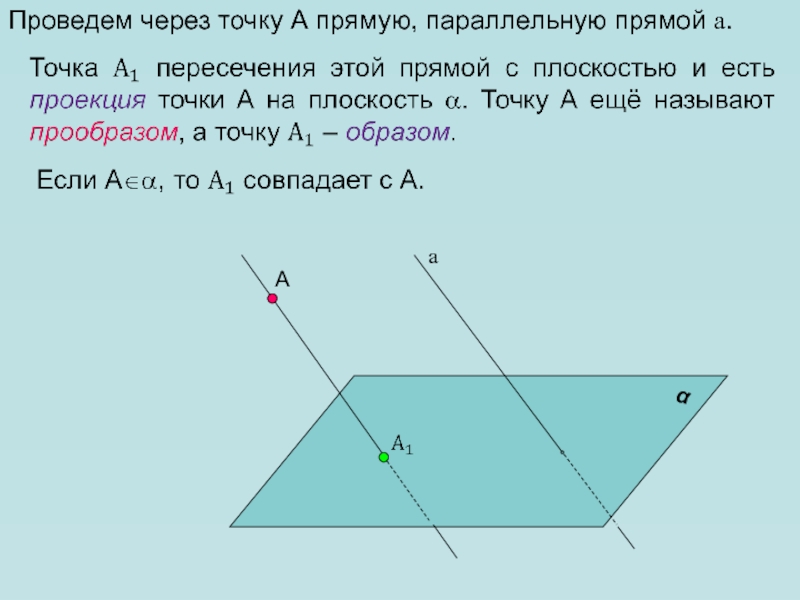
- 4. АаПроведем через точку А прямую, параллельную прямой а.
- 5. Рассматривая любую геометрическую фигуру как множество точек,
- 6. Что такое проекция фигуры на плоскость?
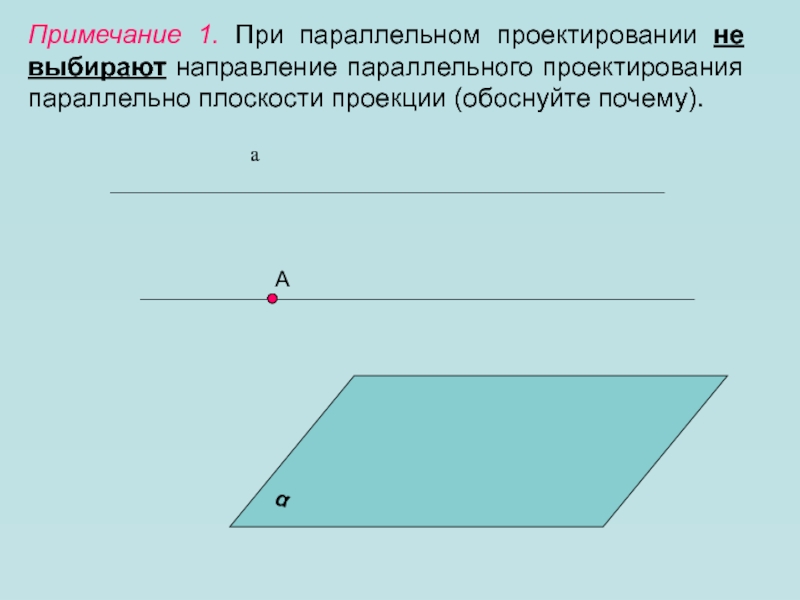
- 7. Примечание 1. При параллельном проектировании не выбирают направление параллельного проектирования параллельно плоскости проекции (обоснуйте почему).Аа
- 8. Примечание 2. При параллельном проектировании плоских фигур
- 9. Примечание 3. Если направление параллельного проектирования перпендикулярно
- 10. Примечание 4. Если плоскость проекций и плоскость,
- 11. Параллельное проектирование обладает свойствами:1) параллельность прямых (отрезков, лучей) сохраняется;аADCB
- 12. 2) отношение длин отрезков, лежащих на
- 13. Параллельное проектирование обладает свойствами:параллельность прямых (отрезков, лучей)
- 14. В каком случае параллельной проекцией прямой будет
- 15. Какие фигуры могут служить проекциями двух пересекающихся
- 16. Какие фигуры могут служить проекциями двух параллельных
- 17. Какие фигуры могут служить проекциями двух скрещивающихся
- 18. Сохраняются ли при параллельном проектировании величины углов? Сохраняются ли при параллельном проектировании длины отрезков?B1?
- 19. Как на параллельной проекции треугольника построить проекцию
- 20. Итак, построим изображение куба:Далее разберем примеры изображения некоторых плоских фигур…
- 21. Фигура в пространствеЕё изображение на плоскостиПроизвольный треугольникПроизвольный треугольникПрямоугольный треугольникПроизвольный треугольникРавнобедренный треугольникПроизвольный треугольник
- 22. Фигура в пространствеЕё изображение на плоскостиРавносторонний треугольникПроизвольный треугольникПараллелограммПроизвольный параллелограммПрямоугольникПроизвольный параллелограмм
- 23. Фигура в пространствеЕё изображение на плоскостиКвадратПроизвольный параллелограммТрапецияПроизвольная трапецияПроизвольный параллелограммРомб
- 24. Фигура в пространствеЕё изображение на плоскостиРавнобокая трапецияПроизвольная трапецияПрямоугольная трапецияПроизвольная трапецияКруг (окружность)Овал (эллипс)
- 25. ABCDEFOРазберемся, как построить изображение правильного шестиугольника.FABCDEРазобьем правильный
- 26. ABCDEКак построить изображение правильного пятиугольника.Разобьем фигуру на
- 27. S AB1C =S ABC cosТеорема 16:
- 28. Слайд 28
- 29. Теорема: Площадь проекции
- 30. Через сторону АС = 10 см равностороннего
- 31. Слайд 31
- 32. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Метод параллельного проектирования. Изображение пространственных фигур на плоскости.
Воробьев Леонид Альбертович,
г.Минск
Слайд 2Итак, мы приступили к изучению стереометрии – геометрии в пространстве.
Как всегда нам необходимо уметь изображать геометрические фигуры, причем все
чертежи мы по-прежнему выполняем на плоскости (на странице тетради, на доске и т.д.). Каким образом пространственную фигуру (например, куб) можно «уложить» в плоскость?Для решения этой задачи применяется метод параллельного проектирования. Выясним его суть на примере простейшей геометрической фигуры – точки.
Итак, у нас есть геометрическая фигура в пространстве – точка А.
А
Слайд 3А
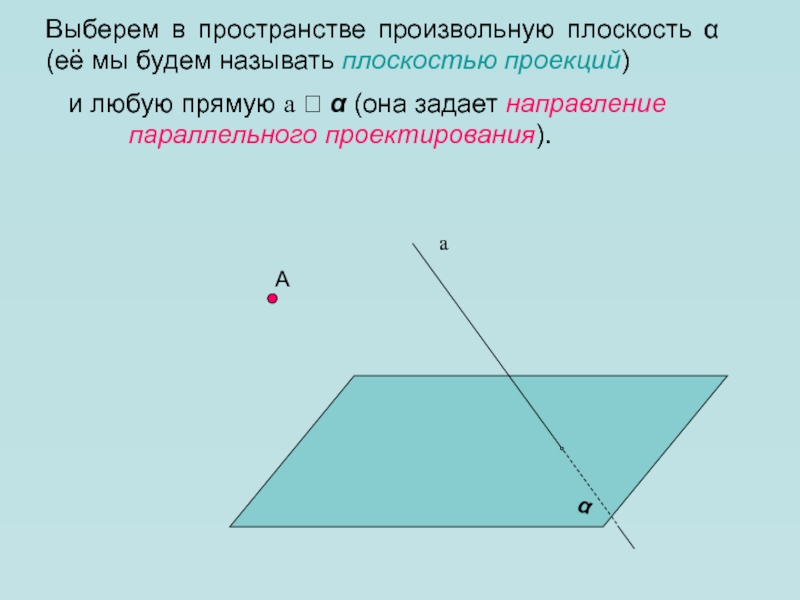
Выберем в пространстве произвольную плоскость (её мы будем называть
плоскостью проекций)
и любую прямую a (она задает направление
параллельного
проектирования).а
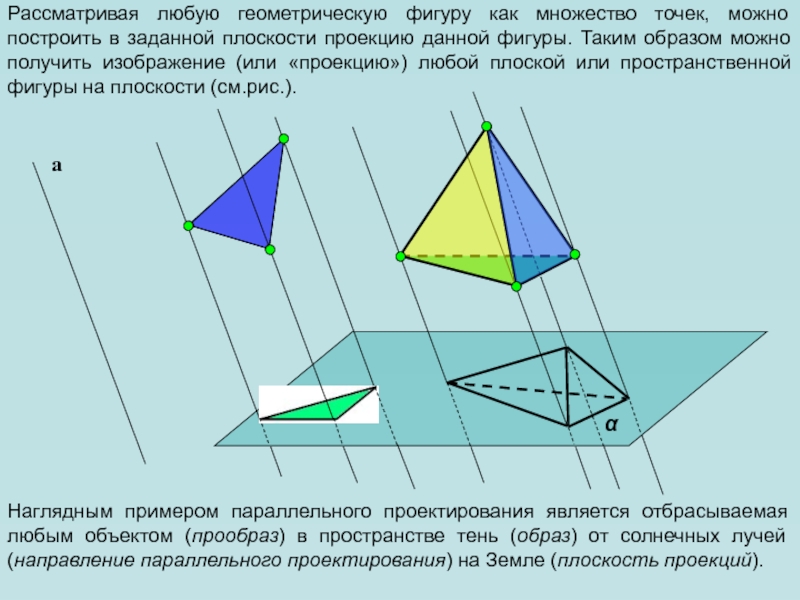
Слайд 5Рассматривая любую геометрическую фигуру как множество точек, можно построить в
заданной плоскости проекцию данной фигуры. Таким образом можно получить изображение
(или «проекцию») любой плоской или пространственной фигуры на плоскости (см.рис.).а
Наглядным примером параллельного проектирования является отбрасываемая любым объектом (прообраз) в пространстве тень (образ) от солнечных лучей (направление параллельного проектирования) на Земле (плоскость проекций).
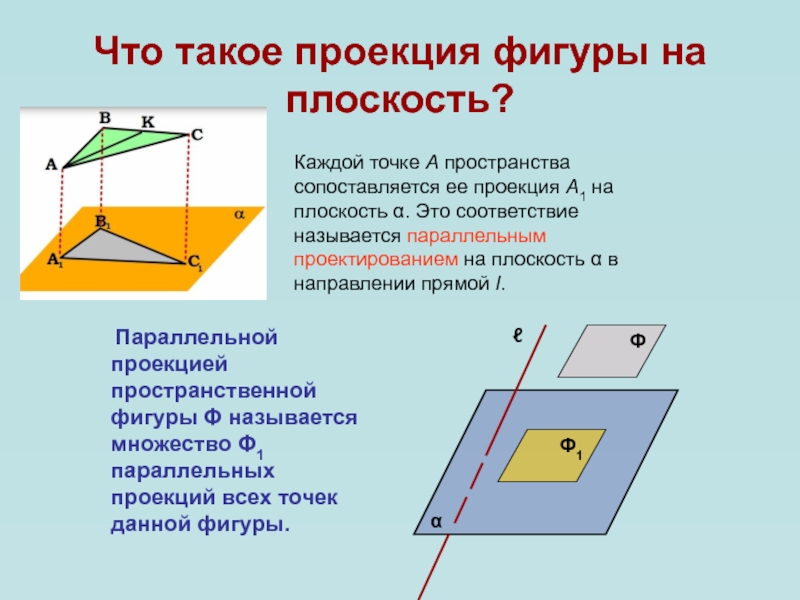
Слайд 6Что такое проекция фигуры на плоскость?
Параллельной
проекцией пространственной фигуры Φ называется множество Φ1 параллельных проекций всех
точек данной фигуры.Каждой точке A пространства сопоставляется ее проекция A1 на плоскость . Это соответствие называется параллельным проектированием на плоскость в направлении прямой l.
Слайд 7Примечание 1. При параллельном проектировании не выбирают направление параллельного проектирования
параллельно плоскости проекции (обоснуйте почему).
А
а
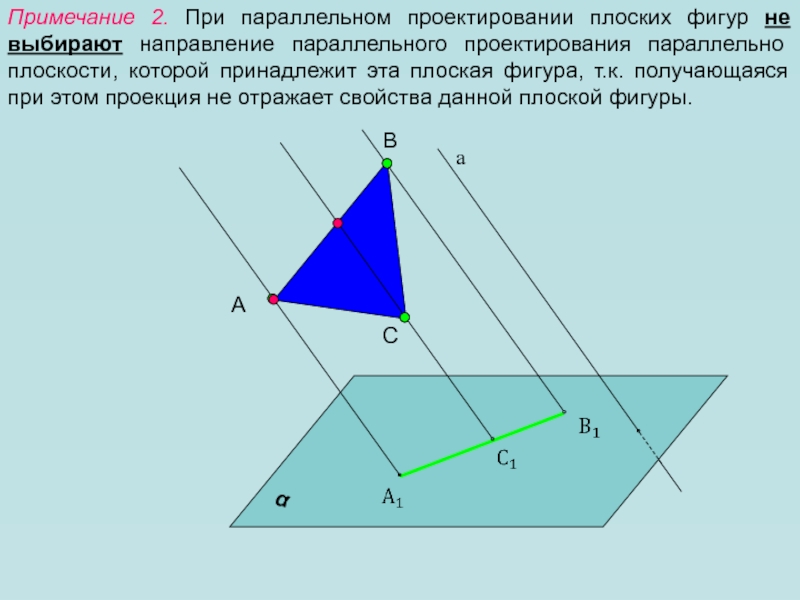
Слайд 8Примечание 2. При параллельном проектировании плоских фигур не выбирают направление
параллельного проектирования параллельно плоскости, которой принадлежит эта плоская фигура, т.к.
получающаяся при этом проекция не отражает свойства данной плоской фигуры.А
а
B
C
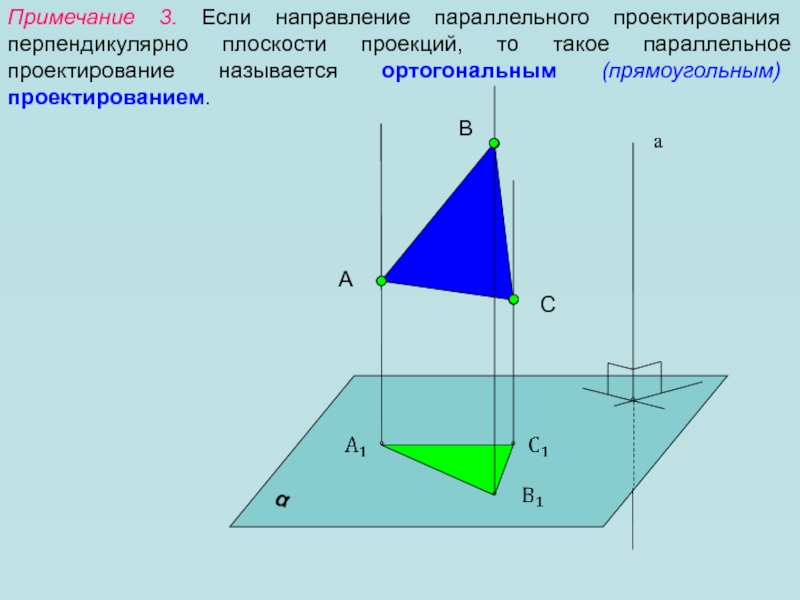
Слайд 9Примечание 3. Если направление параллельного проектирования перпендикулярно плоскости проекций, то
такое параллельное проектирование называется ортогональным (прямоугольным) проектированием.
А
а
B
C
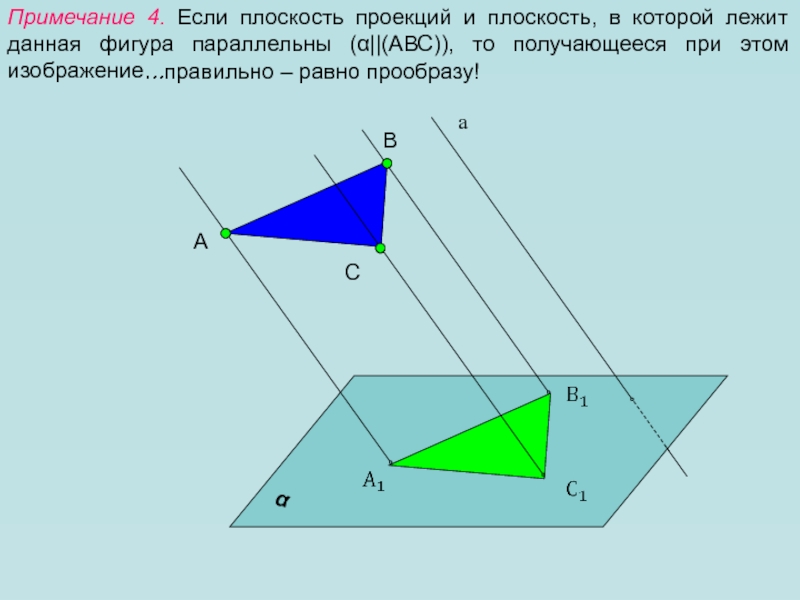
Слайд 10Примечание 4. Если плоскость проекций и плоскость, в которой лежит
данная фигура параллельны (||(АВС)), то получающееся при этом изображение…
А
а
B
C
…правильно
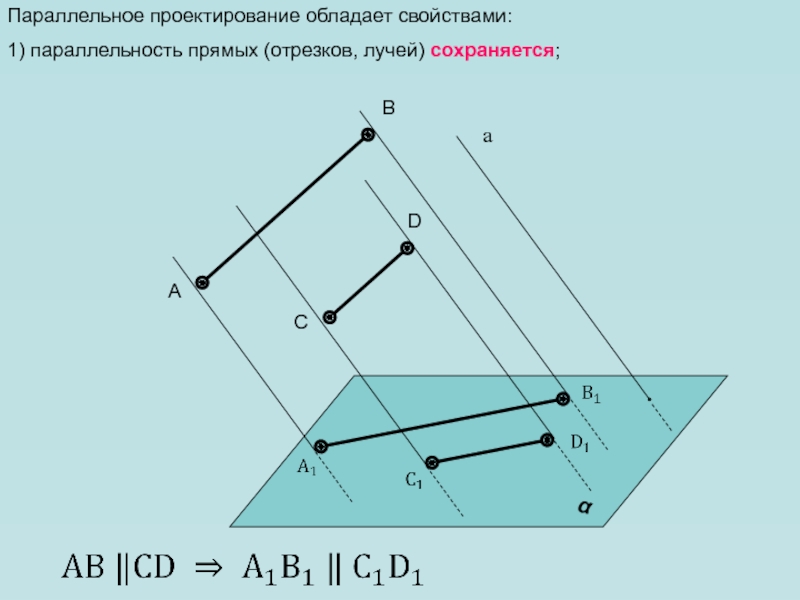
– равно прообразу! Слайд 11Параллельное проектирование обладает свойствами:
1) параллельность прямых (отрезков, лучей) сохраняется;
а
A
D
C
B
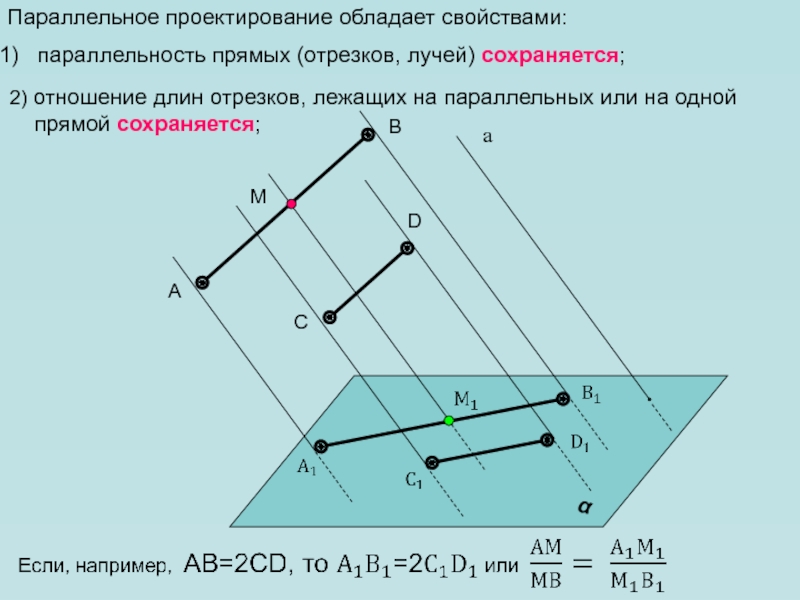
Слайд 12 2) отношение длин отрезков, лежащих на параллельных или на
одной прямой сохраняется;
Параллельное проектирование обладает свойствами:
параллельность прямых (отрезков, лучей) сохраняется;
а
A
D
C
B
М
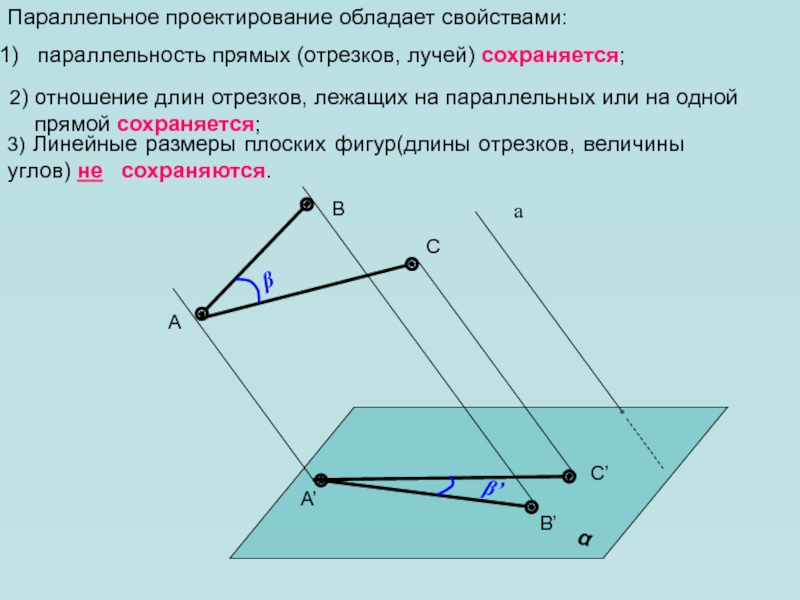
Слайд 13Параллельное проектирование обладает свойствами:
параллельность прямых (отрезков, лучей) сохраняется;
а
A
B
A’
B’
3) Линейные размеры
плоских фигур(длины отрезков, величины углов) не сохраняются.
2) отношение
длин отрезков, лежащих на параллельных или на одной прямой сохраняется;β
β’
C
C’
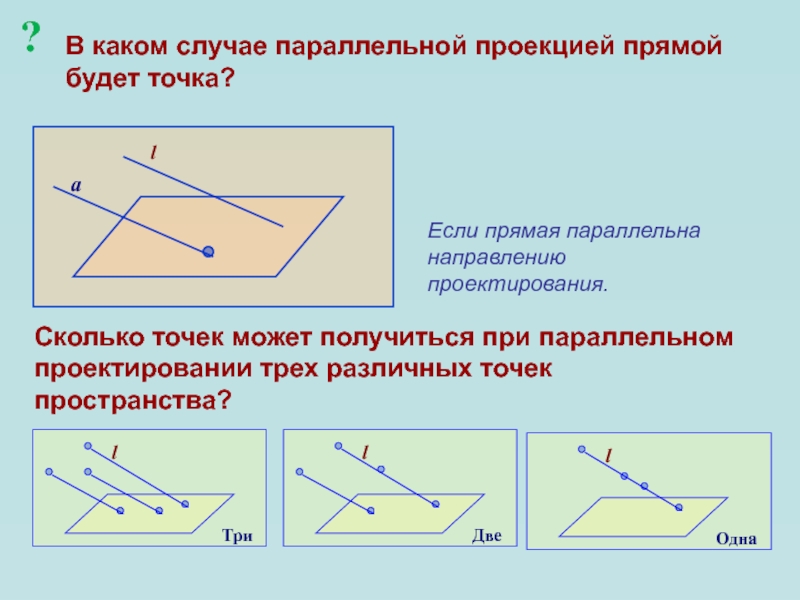
Слайд 14В каком случае параллельной проекцией прямой будет точка?
Если прямая
параллельна направлению проектирования.
Сколько точек может получиться при параллельном проектировании трех
различных точек пространства??
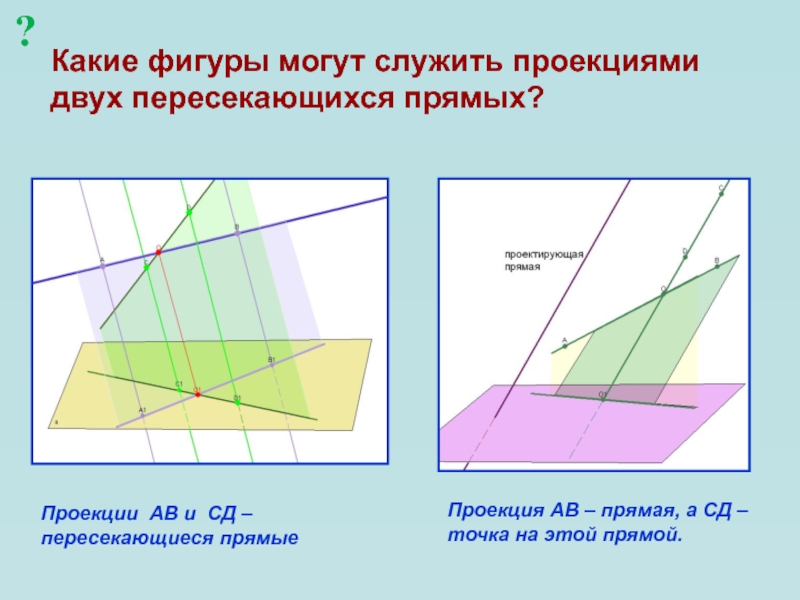
Слайд 15Какие фигуры могут служить проекциями двух пересекающихся прямых?
?
Проекции АВ и
СД – пересекающиеся прямые
Проекция АВ – прямая, а СД –
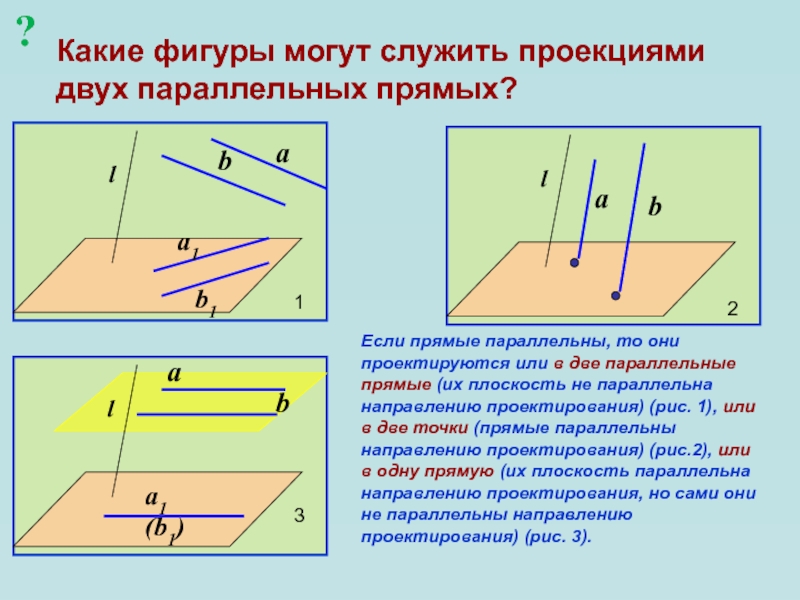
точка на этой прямой.Слайд 16Какие фигуры могут служить проекциями двух параллельных прямых?
1
2
3
Если прямые параллельны,
то они проектируются или в две параллельные прямые (их плоскость
не параллельна направлению проектирования) (рис. 1), или в две точки (прямые параллельны направлению проектирования) (рис.2), или в одну прямую (их плоскость параллельна направлению проектирования, но сами они не параллельны направлению проектирования) (рис. 3).?
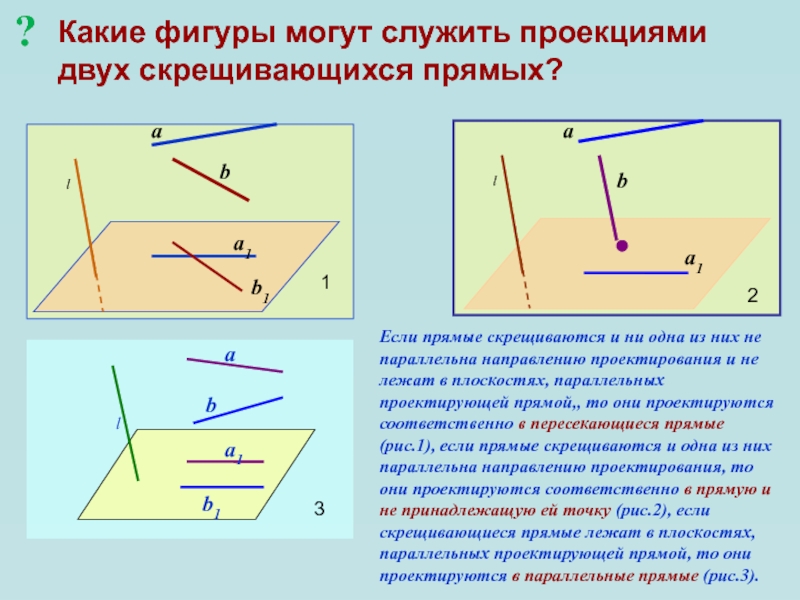
Слайд 17Какие фигуры могут служить проекциями двух скрещивающихся прямых?
Если прямые скрещиваются
и ни одна из них не параллельна направлению проектирования и
не лежат в плоскостях, параллельных проектирующей прямой,, то они проектируются соответственно в пересекающиеся прямые (рис.1), если прямые скрещиваются и одна из них параллельна направлению проектирования, то они проектируются соответственно в прямую и не принадлежащую ей точку (рис.2), если скрещивающиеся прямые лежат в плоскостях, параллельных проектирующей прямой, то они проектируются в параллельные прямые (рис.3).1
2
3
?
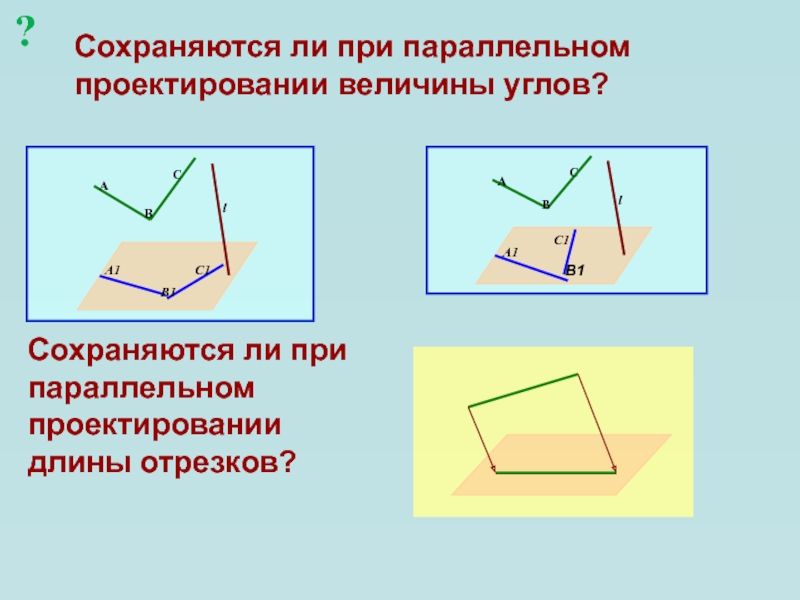
Слайд 18Сохраняются ли при параллельном проектировании величины углов?
Сохраняются ли при параллельном
проектировании длины отрезков?
B1
?
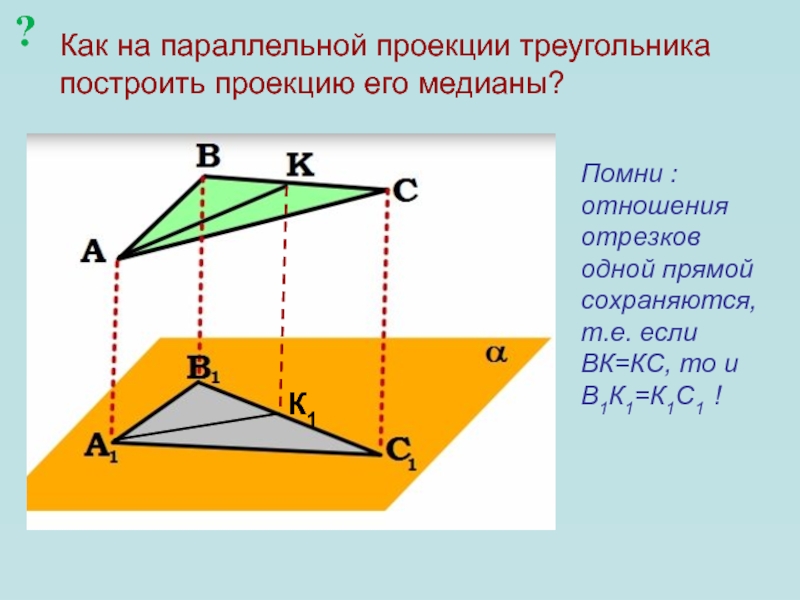
Слайд 19Как на параллельной проекции треугольника построить проекцию его медианы?
К1
Помни :
отношения отрезков одной прямой сохраняются, т.е. если ВК=КС, то и
В1К1=К1С1 !?
Слайд 20
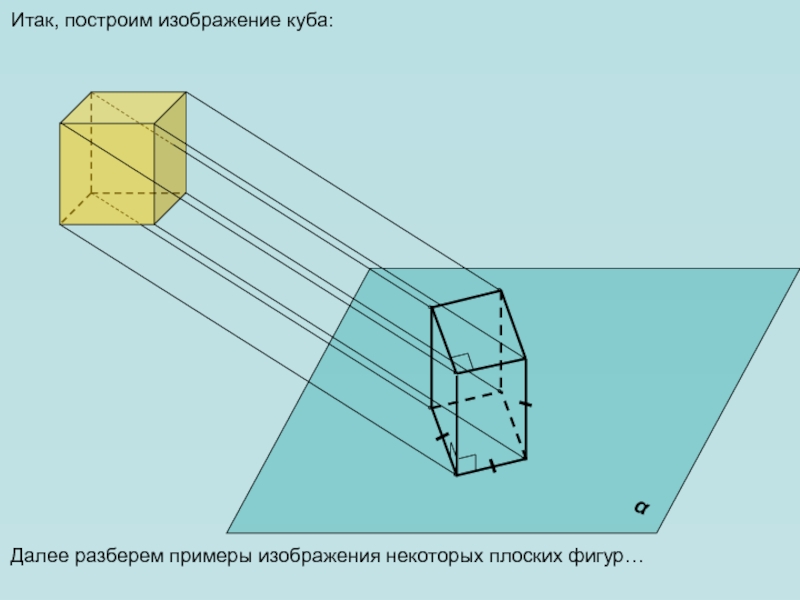
Итак, построим изображение куба:
Далее разберем примеры изображения некоторых плоских фигур…
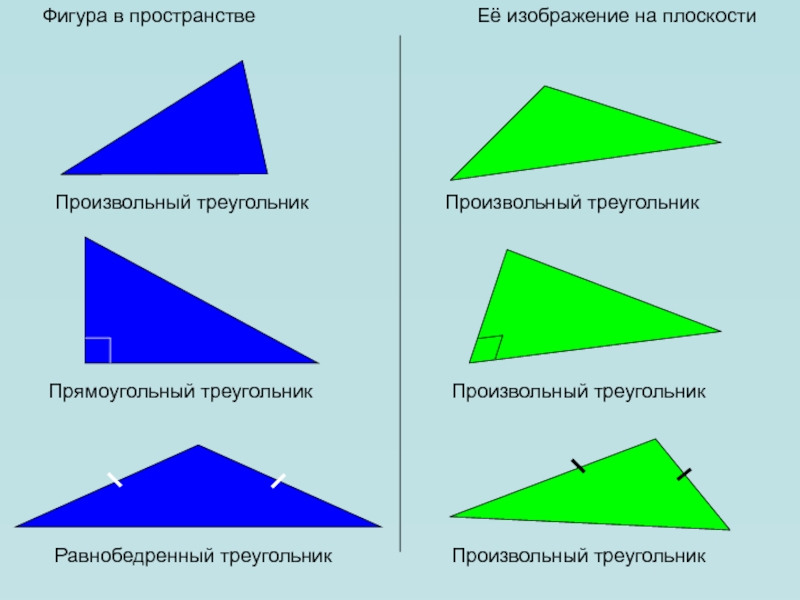
Слайд 21Фигура в пространстве
Её изображение на плоскости
Произвольный треугольник
Произвольный треугольник
Прямоугольный треугольник
Произвольный треугольник
Равнобедренный
треугольник
Произвольный треугольник
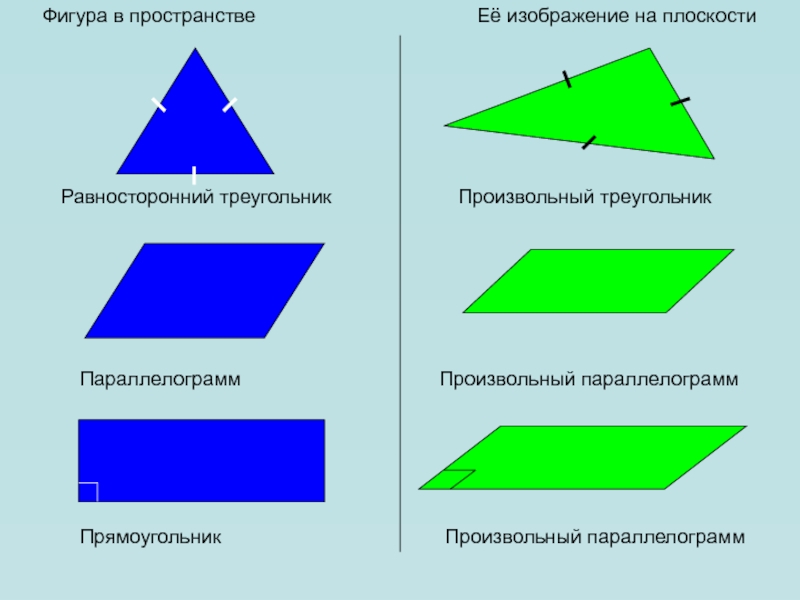
Слайд 22Фигура в пространстве
Её изображение на плоскости
Равносторонний треугольник
Произвольный треугольник
Параллелограмм
Произвольный параллелограмм
Прямоугольник
Произвольный параллелограмм
Слайд 23Фигура в пространстве
Её изображение на плоскости
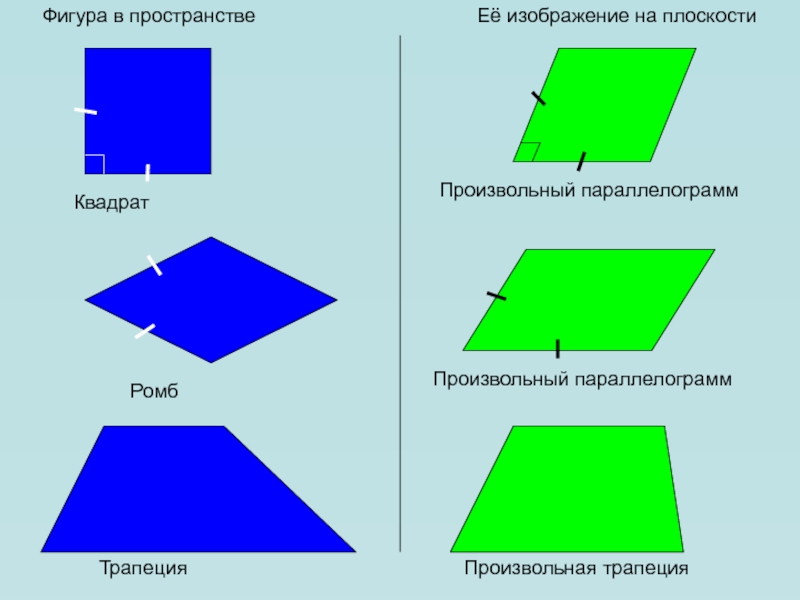
Квадрат
Произвольный параллелограмм
Трапеция
Произвольная трапеция
Произвольный параллелограмм
Ромб
Слайд 24Фигура в пространстве
Её изображение на плоскости
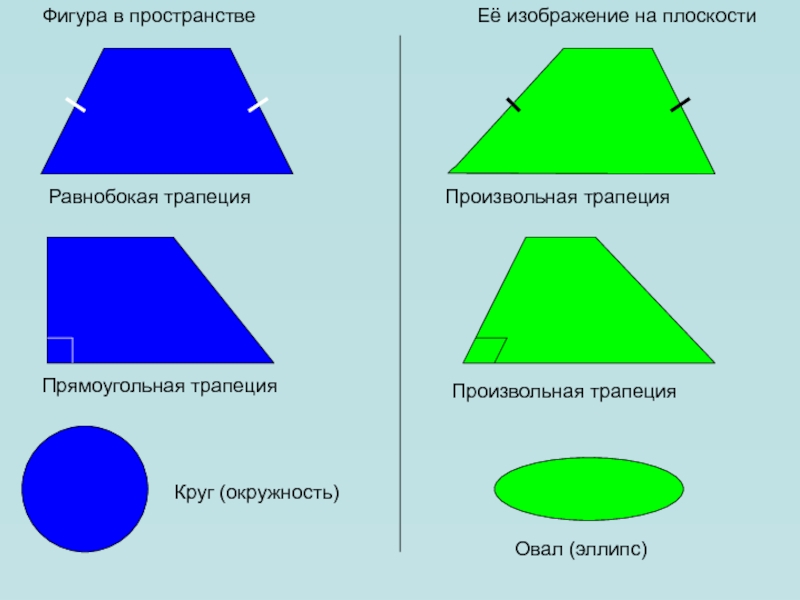
Равнобокая трапеция
Произвольная трапеция
Прямоугольная трапеция
Произвольная трапеция
Круг
(окружность)
Овал (эллипс)
Слайд 25A
B
C
D
E
F
O
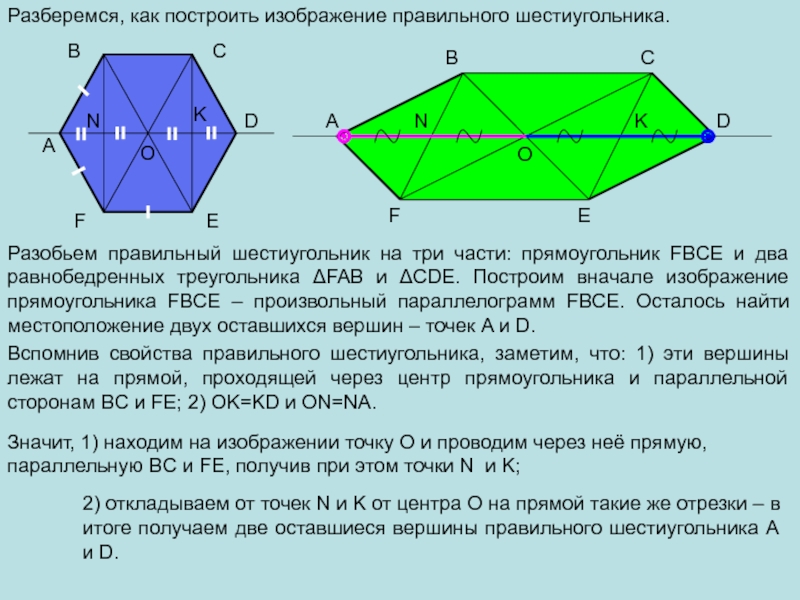
Разберемся, как построить изображение правильного шестиугольника.
F
A
B
C
D
E
Разобьем правильный шестиугольник на три
части: прямоугольник FBCE и два равнобедренных треугольника ΔFAB и ΔCDE.
Построим вначале изображение прямоугольника FBCE – произвольный параллелограмм FBCE. Осталось найти местоположение двух оставшихся вершин – точек A и D.Вспомнив свойства правильного шестиугольника, заметим, что: 1) эти вершины лежат на прямой, проходящей через центр прямоугольника и параллельной сторонам BC и FE; 2) OK=KD и ON=NA.
K
N
Значит, 1) находим на изображении точку О и проводим через неё прямую, параллельную BC и FE, получив при этом точки N и K;
O
N
K
2) откладываем от точек N и K от центра О на прямой такие же отрезки – в итоге получаем две оставшиеся вершины правильного шестиугольника A и D.
Слайд 26A
B
C
D
E
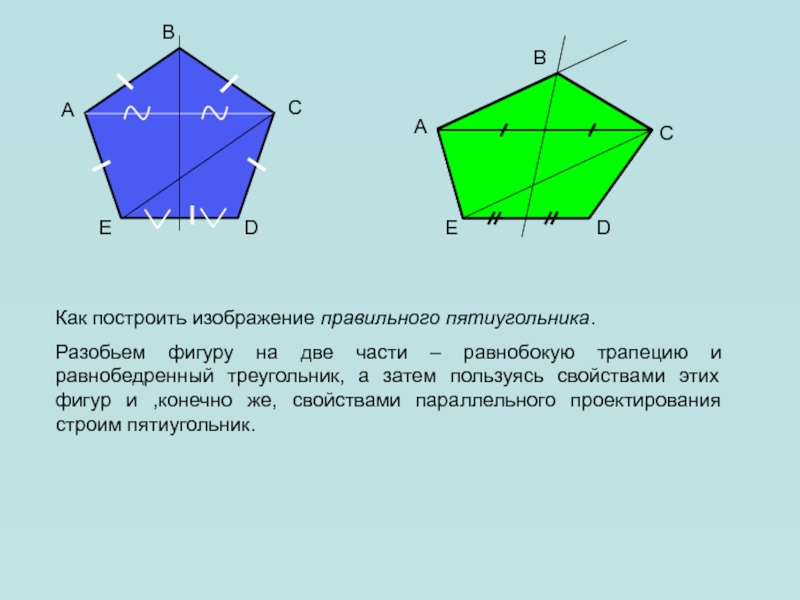
Как построить изображение правильного пятиугольника.
Разобьем фигуру на две части –
равнобокую трапецию и равнобедренный треугольник, а затем пользуясь свойствами этих
фигур и ,конечно же, свойствами параллельного проектирования строим пятиугольник.A
C
D
E
B
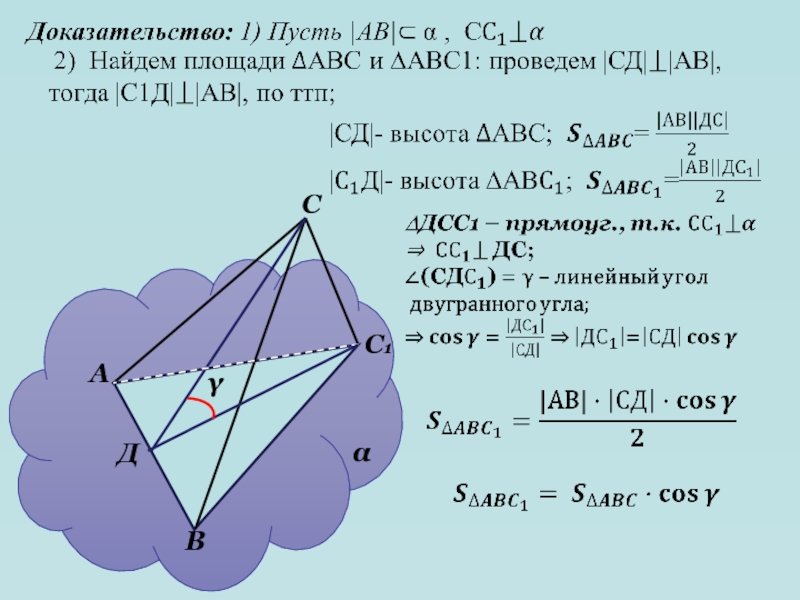
Слайд 27S AB1C =S ABC cos
Теорема 16: Площадь ортогональной проекции
треугольника равна произведению площади треугольника на косинус угла между их
плоскостями.Дано: АВС
АВС1 – ортогональная
проекция на плоскость .
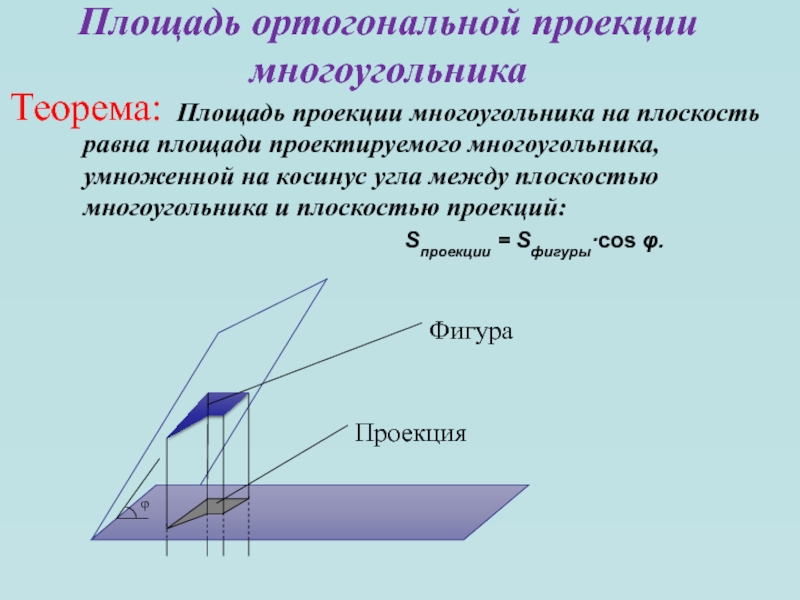
Слайд 29Теорема:
Площадь проекции многоугольника на плоскость
равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью
многоугольника и плоскостью проекций:Sпроекции = Sфигуры·cos φ.
Площадь ортогональной проекции многоугольника
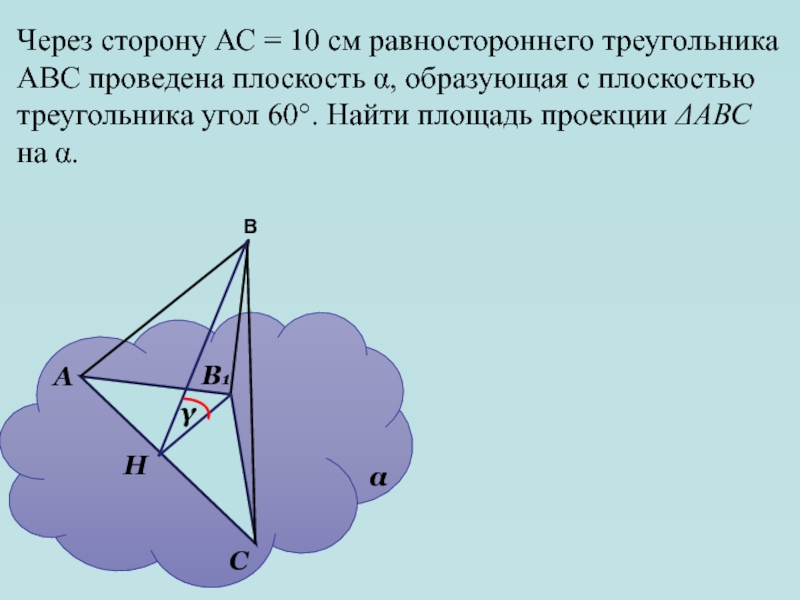
Слайд 30Через сторону АС = 10 см равностороннего треугольника АВС проведена
плоскость α, образующая с плоскостью треугольника угол 60°. Найти площадь
проекции АВСна α.
А
С
В1
Н
В