Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методика изучения площади
Содержание
- 1. Методика изучения площади
- 2. Площадь-это…1)…некая величина, характеризующая геометрическую фигуру, расположенную на
- 3. История развития понятия площади и её измерения.
- 4. Около 4 000 лет назад египтяне использовали
- 5. Для того чтобы найти площадь трапеции египтяне
- 6. Так же нужно отметить, что в Египте пользовались формулой нахождения площади четырехугольника:S = a+b∙c+d
- 7. В математических трудах Герона, Евклида и многих
- 8. Греческие математики всерьёз заинтересовались задачами на деление
- 9. Еще с давних времен математики стремились превращать
- 10. Далее из параллелограмма делали равновеликий ему прямоугольник
- 11. Измерение площади на РусиНа Руси впервые заговорили
- 12. Книга сошного письмаСошное письмо«Книга сошного письма» -
- 13. Л.Ф.МагницкийВ 1701 году при Петре I в
- 14. Труды многих ученых повлияли на современное восприятие
- 15. Свойства площади:1) площадь фигуры не изменяется при
- 16. Мерки для измерения площадейДля измерения площадей используют
- 17. Отличие площади от объемаОбъем - это пространство,
- 18. Слайд 18
- 19. В методике выделяют следующие этапы изучения величин
- 20. Методика изучения площади фигур1 этап. Уточнение жизненных
- 21. 2 этап. Сравнение площадей разными способами (
- 22. В) использование различных мерок. Создаем проблемную ситуацию,
- 23. Дети подсчитывают количество мерок, поместившихся в каждой
- 24. Сначала дети закрывают фигуры моделями квадратных см
- 25. Предлагаем прямоугольник, разбитый на квадраты , нужно
- 26. 4 этап. Сложение и вычитание величин, выраженных
- 27. Учитель предлагает детям рассмотреть рисунок 2.С помощью
- 28. Далее дети читают и записывают таблицу единиц
- 29. Знакомство с аром и гектаромДалее учитель знакомит
- 30. М4М ч.1 с. 431) посчитаем число полных
- 31. 6 этап. Сложение и вычитание величин, выраженных
- 32. 7 этап. Умножение и деление величины на
- 33. Площадь фигуры(Аргинская)1 этап. Уточнение жизненных представлений, введение
- 34. Какая фигура занимает больше места на странице?
- 35. А3М ч.1 с.5В) использование различных мерок. Создаем
- 36. 3этап. Введение единой меры ( единицы измерения)
- 37. На следующем уроке учащихся знакомят с правилом
- 38. 4 этап. Сложение и вычитание величин, выраженных
- 39. Площадь и ее величиныА3М ч.1 с.32
- 40. 6 этап. Сложение и вычитание величин, выраженных
- 41. Площадь фигуры (Демидова, козлова, Тонких)1 этап.
- 42. Фигуры из задания 1 разбили на квадраты
- 43. Дети сравнивают площади фигурБ) Сравнение способом наложения .Сформулировать ответ на основной вопрос урока
- 44. В) использование различных мерок. Создаем проблемную ситуацию,
- 45. Слайд 45
- 46. 3 этап. Введение единой меры ( единицы
- 47. Слайд 47
- 48. Вводим палетку. Это прозрачная пленка, расчерченная на
- 49. Слайд 49
- 50. 4 этап. Сложение и вычитание величин, выраженных
- 51. Учитель спрашивает, смогли ли они выполнить задание?
- 52. 6 этап. Сложение и вычитание величин, выраженных
- 53. 7 этап. Умножение и деление величины на
- 54. Спасибо за внимание!
- 55. Скачать презентанцию
Площадь-это…1)…некая величина, характеризующая геометрическую фигуру, расположенную на плоскости или на иной поверхности;
Слайды и текст этой презентации
Слайд 1«Методика изучения площади»
Выполнила: студент 4 курса
Пыжикова А.А.
группа ЗНО-116
Приняла: старший преподаватель
Болотова
Т.В.
Слайд 2Площадь-это…
1)…некая величина, характеризующая геометрическую фигуру, расположенную на плоскости или на
иной поверхности;
или2)…место, которое занимает фигура на плоскости.
Обозначается эта величина буквой S.
Площадь принято определять у плоских замкнутых фигур.
Слайд 3История развития понятия площади и её измерения.
Более 4 тысяч
лет назад площади земельных участков в форме трапеции и
прямоугольника, научились
вычислять в квадратных единицах еще вВавилоне. В то время за единицу измерения площади брали квадрат,
потому что именно он обладал подходящими свойствами. К этим
свойствам можно отнести: равные стороны, прямые и равные углы, ось и
центр симметрии. Квадраты легко строить, с их помощью можно покрыть
фигуру любой формы.
Слайд 4Около 4 000 лет назад египтяне использовали те же приемы,
что и мы, для определения площади прямоугольника, параллелограмма,
треугольника и трапеции.
Таким образом, чтобы определить площадьпрямоугольника, египтяне умножали длину на ширину; чтобы найти
площадь треугольника, основание треугольника делили пополам и
умножали на высоту.
Слайд 5Для того чтобы найти площадь трапеции египтяне находили сумму параллельных
сторон, делили пополам и умножали на высоту. При разбиении многоугольника
на треугольники, прямоугольники и трапеции находили и его площадь. Египтяне использовали множество других способов, которые помогали им быстро вычислить площадь земельных участков. Например, они использовали такой прием, как обход участка по его границе, но чаще всего результат измерения получался с некоторой погрешностью.Слайд 6Так же нужно отметить, что в Египте пользовались формулой нахождения
площади четырехугольника:
S = a+b∙c+d
Слайд 7В математических трудах Герона, Евклида и многих других ученых было
отмечено, что греки и индусы ушли намного дальше. По мнению
Евклида, фигура – это часть плоскости, ограниченная той или иной замкнутой линией, следовательно, под понятием фигуры уже подразумевается ее площадь. Евклид не выражал результат измерения площади числом. Он сравнивал площади различных фигур между собой.Слайд 8Греческие математики всерьёз заинтересовались задачами на деление площади фигур с
помощью пересекающих прямых, а так же превращением одной фигуры в
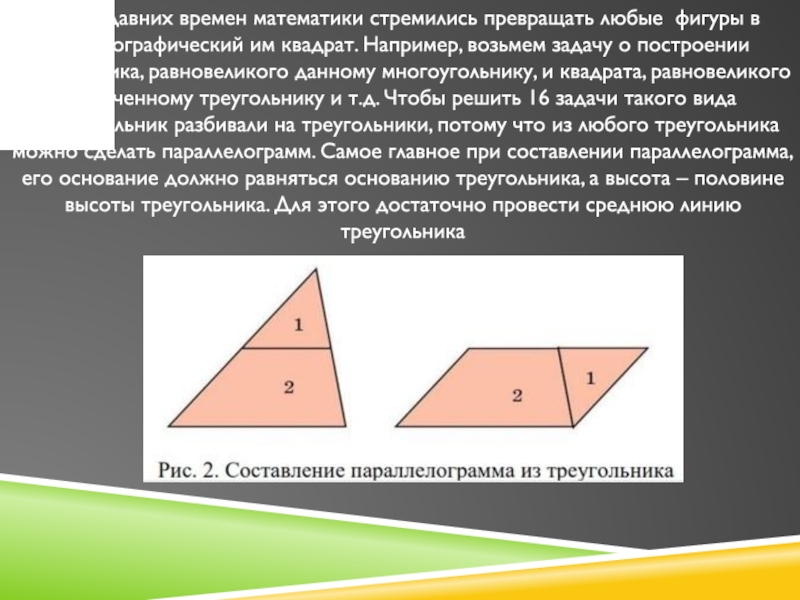
другую. Превращение происходило при помощи разрезания фигуры на части и составления из них новой фигуры. Именно задачи данного типа выдвигались землемерием и архитектурными работами.Слайд 9Еще с давних времен математики стремились превращать любые фигуры в
гомолографический им квадрат. Например, возьмем задачу о построении треугольника, равновеликого
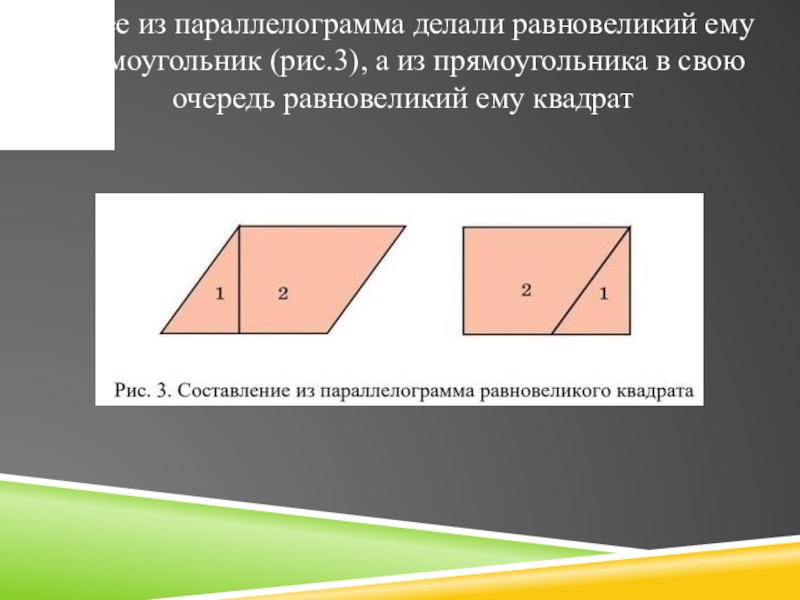
данному многоугольнику, и квадрата, равновеликого полученному треугольнику и т.д. Чтобы решить 16 задачи такого вида многоугольник разбивали на треугольники, потому что из любого треугольника можно сделать параллелограмм. Самое главное при составлении параллелограмма, его основание должно равняться основанию треугольника, а высота – половине высоты треугольника. Для этого достаточно провести среднюю линию треугольникаСлайд 10Далее из параллелограмма делали равновеликий ему прямоугольник (рис.3), а из
прямоугольника в свою очередь равновеликий ему квадрат
Слайд 11Измерение площади на Руси
На Руси впервые заговорили об измерении площади
и расстояния примерно в XI веке. В Государственном Эрмитаже хранится
камень с надписью о том, что в 1068 году было измерено расстояние через Керченский пролив от города Тамань до города Керчь. Это расстояние равнялось 14 тысячам сажень или 29,8704 километров.На Руси выдвигали общие правила для вычисления площади, которые были верными в некоторых случаях. Во второй половине XVI в. создавались рукописи с геометрическим содержанием, т.к. возросли потребности в измерении площади земли, в развитии артиллерийского дела и строительстве городов.
Слайд 12Книга сошного письма
Сошное письмо
«Книга сошного письма» - это древнейший экземпляр
из сохранившихся рукописей о правилах измерения площади. Этот экземпляр относится
к 1629 г., но имеются предположения, что в 1556 г. Иваном Грозным был составлен оригинал. В этой книге имеется глава «О земном верстании, как земля верстать», но в ней много неверного материала о способах измерения площадей. Если задуматься, то эти искажения могли появиться из-за переписывания от руки.Слайд 13Л.Ф.Магницкий
В 1701 году при Петре I в Москве открыли «Математические
и навигатские школы». Данная школа принесла огромный вклад в изучение
геометрического материала. В программу обучения были включены такие дисциплины, как алгебра, геометрия, арифметика и тригонометрия. Эти науки преподавал выписанный из-за границы профессор-математик Форварсон и математик-самоучка Леонтий Магницкий.Слайд 14Труды многих ученых повлияли на современное восприятие понятия. Многие тысячелетия
изучались свойства фигур и их измерение. Люди с легкостью могут
представить, что такое площадь комнаты или участка земли. Так же они могут определить, что если земельные участки одинаковы, то их площадь равна, а площадь квартиры складывается из площади комнат. Все это складывается в обыденное представление понятие, но даже это относится к геометрическому материалу.Слайд 15Свойства площади:
1) площадь фигуры не изменяется при изменении ее положения
на плоскости;
2) часть предмет всегда меньше целого;
3) из одних и
тех же заданных фигур можно составить различные геометрические фигуры Слайд 16Мерки для измерения площадей
Для измерения площадей используют разные мерки. Квадратный
сантиметр – это квадрат со стороной в 1 см, квадратный
дециметр – это квадрат со стороной в 1 дм, квадратный метр – это квадрат со стороной в 1 мДля измерения больших площадей используют квадратный километр – это квадрат, сторона которого равна 1 км.
Слова «квадратный километр» сокращенно при числе записывают так – 1 км2, 3 км2, 12 км2. В квадратных километрах измеряют, например, площади городов, площадь Москвы S = 1091 км2.
Слайд 17Отличие площади от объема
Объем - это пространство, которое занимает фигура,
(то есть, сколько внутрь воды поместится)
Площадь - это то,
чем она ограничена. (то есть, какого размера будет лист бумаги, которым ее обклеят снаружиСлайд 19В методике выделяют следующие этапы изучения величин :
1 этап. Ознакомление
с величиной на основе уточнения жизненных представлений учащихся.
2 этап. Сравнение
величин разными способами:- «на глаз» или с помощью ощущений;
- с помощью приемов наложения или приложения;
- с помощью различных мерок
3 этап. Введение единицы измерения. Формирование измерительных навыков
4 этап. Сложение и вычитание величин, выраженных в одной единице измерения
5 этап. Введение других единиц измерения величины. Перевод из одной единицы в другую.
6 этап. Сложение и вычитание величин, выраженных в единицах двух наименований
7 этап. Умножение и деление величин на число .
Слайд 20Методика изучения площади фигур
1 этап. Уточнение жизненных представлений, введение понятия
«Площадь».
М3Мч.1 стр. 56
При введении площади на специальном уроке к доске
прикрепляем несколько фигур.На доске несколько кругов разного размера . Предлагаем сравнить их между собой
Чем похожи? ( формой)
Чем отличаются? ( цветом, размером)
Что понимают под размером в этом случае?
Учитель сообщает, что на данном этапе под размером понимают площадь фигуры. Это место, которое фигура занимает на поверхности чего- либо. Обводим круги на доске мелом, снимаем их . Дети видят, что круги занимают разное место на поверхности доски, значит площадь некоторых кругов больше , других меньше.
Слайд 212 этап. Сравнение площадей разными способами ( этот этап идет
одновременно с первым)
А) «на глаз» - визуально . Предлагаем для
сравнения контрастные по площади фигуры .Дети сравнивают и в ответах использую терминологию .Например : площадь красного круга больше площади зеленого квадрата и т.д.Б) Сравнение способом наложения .
Если одна фигура полностью помещается внутри другой , то площадь первой фигуры меньше площади второй.
М3Мч.1 стр. 56
Слайд 22В) использование различных мерок. Создаем проблемную ситуацию, когда способы А
и В неудобны
Предлагаем сравнить эти фигуры по площади , но
способы А и Б не дают результатов . переворачиваем фигуры , а там они расчерчены на мерки ( квадраты)Слайд 23Дети подсчитывают количество мерок, поместившихся в каждой фигуре, и сравнивают
эти числа.
Далее даем множество упражнений на нахождение площадей с помощью
различных мерок.( Смотри в М3Мч.1 стр. 56-57 ). Сначала дети закрывают фигуру мерками и считают их, но затем мерок не хватает Тогда расчерчиваем фигуру на мерки ( на фигуре должны появится квадраты ) .Фигуры лучше вырезать из клетчатой бумаги3 этап. Введение единой меры ( единицы измерения) площади.
М3Мч.1 стр.58
Площадь квадрата, сторона которого 1см, - это единица площади - квадратный сантиметр.
Выдаем на парту фигуры, состоящие из целого числа см2
Слайд 24Сначала дети закрывают фигуры моделями квадратных см полностью .
Потом создаем
проблемную ситуацию: моделей не хватает , чтобы полностью закрыть фигуру
расчерчиваем ее на см2. Но это неудобно , ( Таких заданий 1-2)Вводим палетку. Это прозрачная пленка, расчерченная на см2. Кладем ее на фигуру и считаем см2 .
На следующем уроке учащихся знакомят с правилом нахождения площади прямоугольника
М3М ч.1 с.60
Слайд 25Предлагаем прямоугольник, разбитый на квадраты , нужно найти площадь прямоугольника.
Эту задачу можно решить 2 способами.
1) Замечаем, что прямоугольник разбит
на столбцы, их 8 и в каждом по 3 квадрата.3*8=48 см2
Чем являются числа 3 и 8 на данном рисунке? ( это числовые значения длин сторон длину одной стороны * на длину второй стороны. Или длину * на ширину. Замечаем, что на рисунке можно выделить 3 одинаковые строки ,каждая по 8 квадратов: 8*3=24 Аналогично 8 и 3числовые значения длин сторон .Длину * на ширину получаем площадь .Делаем общий вывод .
Чтобы вычислить площадь прямоугольника , нужно длину умножить на ширину.
Пользуясь этим правилом, учимся находить площадь прямоугольника.
Слайд 264 этап. Сложение и вычитание величин, выраженных в единицах одного
наименования.
Например: площадь квадрата 16 см2 , а площадь прямоугольника на
24 см2 больше.Найти площадь прямоугольника.
16 см2+ 24 см2
5 этап. Введение других единиц измерения величины. Перевод из одной единицы в другую.
Учитель повторяет с детьми единицы площади, начиная с квадратного сантиметра.
Далее сообщает, что для измерения больших площадей используют квадратный километр. Это площадь квадрата , сторона которого равна 1 км. Слова «квадратный километр» записывают так: 1 км2, 8 км2, 140 км2. Например, площадь России занимает более 17 000 000 км2.
Так же на данном этапе урока изучают квадратный миллиметр-площадь квадрата, сторона которого равна 1 мм ,который используют для измерения маленьких площадей.
Сокращенно записывают 1 мм2, 9 мм2, 70 мм2.
М4М ч.1 с.39
Для черчения и измерения фигур дети используют миллиметровую бумагу.
Далее дети переходят к практическим заданиям.
Слайд 27Учитель предлагает детям рассмотреть рисунок 2.
С помощью миллиметровой бумаги, они
сравнивают 2 изображенных фигуры и узнают длину и ширину каждой
из этих фигур. Затем, зная формулу нахождения площади, они сравнивают эти фигуры и узнают, какая из них больше другой.Дети выполняют следующее задание.
Нужно найти площадь прямоугольника ABCD и квадрата KMOE в квадратных сантиметрах и выразить ее в квадратных миллиметрах.
С помощью линейки дети измеряют длину и ширину прямоугольника. Т.к в квадрате все стороны равны, то длина=ширине. Поэтому дети замеряют одну сторону квадрата. Тем самым , по формуле площади мы узнаем площадь квадрата и прямоугольника. Нам известно, что 1 кв.см=100 кв.мм.
Поэтому площадь из см2 переводим в мм2
М4М ч.1 с.39
Слайд 28Далее дети читают и записывают таблицу единиц площади.
М4М ч.1 с.41
Пользуясь
таблицей выше , дети закрепляют пройденный материал, но чтобы им
было легче, разбираем способ вычисления этих значенийМ4М ч.1с.41
Любая единица площади -это квадрат с определенной стороной, надо найти его площадь
Например:1 км2
1км2- это квадрат со стороной 1км. 1км=1000м. Площадь квадрата = 1000м*1000м=1000 000 м
Далее дают задания на перевод из одной единицы в другую . Например: 3а=......м2
На этом этапе детей продолжают знакомить с палеткой , но здесь палетку используют для измерения площадей фигур с неровными краями.
Слайд 29
Знакомство с аром и гектаром
Далее учитель знакомит детей с аром
и гектаром
Ар- это площадь квадрата со стороной 10м.
1а= 100м2, потому
его часто называют соткойГектар - это площадь квадрат со стороной 100м.
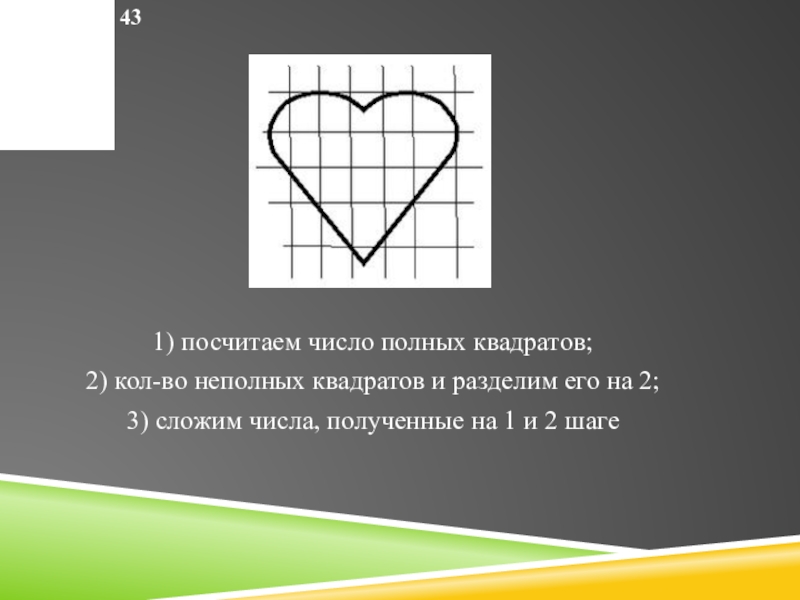
Слайд 30М4М ч.1 с. 43
1) посчитаем число полных квадратов;
2) кол-во неполных
квадратов и разделим его на 2;
3) сложим числа, полученные на
1 и 2 шагеСлайд 316 этап. Сложение и вычитание величин, выраженных в единицах двух
наименований.
Дети выполняют устные и письменные выражения
Случаи без перехода через меру
рассматривают устно. С переходом - письменно в столбикТакие вычисления проводят без перевода из одной меры в другую.
а) устные вычисления. - в строчку:
3км2 46м2+ 2м213см2=3км2 48м2 213см2
б) письменные вычисления - с предварительным переводом в более мелкие меры
54га 15 а -28га57а
5415
-
2857
________________ 2558а=25га28а
2558
Слайд 327 этап. Умножение и деление величины на число.
М;М ч.1 с.76
Рассматривают
2 случая:
а) устные;
3га15а*8=25га20аб) письменные.
26м 85см*7=187 м 95см
2685
* 7
________
18795
Слайд 33Площадь фигуры(Аргинская)
1 этап. Уточнение жизненных представлений, введение понятия «Площадь».
А3М ч.1
с.3
При введении площади на специальном уроке рассматриваем в учебнике 2
рисункаУчитель задает вопрос, знают ли дети, что такое площадь?
Что они понимают под этим словом?
В каких случаях слово «площадь»
имеет значение математическое?
Слайд 34Какая фигура занимает больше места на странице? Говорят,что у этой
фигуры площадь больше. У какой фигуры площадь меньше?
Дети сравнивают площади
обложек учебника математики и альбома для рисования, дневника и тетради.2 этап. Сравнение площадей разными способами ( этот этап идет одновременно с первым)
А) «на глаз» - визуально. Предлагаем для сравнения контрастные по площади фигуры .Дети сравнивают и в ответах использую терминологию .Например : площадь красного круга больше площади зеленого квадрата и т.д
Б) Сравнение способом наложения .
Слайд 35А3М ч.1 с.5
В) использование различных мерок. Создаем проблемную ситуацию, когда
способы А и В неудобны .
Какую мерку вы считаете
наиболее удобной?Почему?
Слайд 363этап. Введение единой меры ( единицы измерения) площади.
А3М ч.1 с.14
Площадь
квадрата, сторона которого 1см, - это единица площади - квадратный
сантиметр .Выдаем на парту фигуры, состоящие из целого числа см2
Сначала дети закрывают фигуры моделями квадратных см полностью .
Потом создаем проблемную ситуацию: моделей не хватает , чтобы полностью закрыть фигуру расчерчиваем ее на см2. Но это неудобно , ( Таких заданий 1-2)
Алгоритм приближённого вычисления площади фигуры с помощью палетки:
1. Положить палетку на чертёж фигуры так, чтобы палетка полностью покрывала фигуру.
2. Сосчитать число квадратов, которые целиком лежат внутри фигуры.
З. Сосчитать число квадратов, через которые проходит контур фигуры и которыe лежат частью вне, частью внутри фигуры.
4. Разделить число неполных квадратов на 2.
5. Сложить число квадратов, которые целиком лежат внутри фигуры, и половину числа квадратов, через которыe проходит контур
фигуры
Слайд 37На следующем уроке учащихся знакомят с правилом нахождения площади прямоугольника
А3М
ч.1 с.24
Дети рассматривают таблицу. Площади этих прямоугольников находили, разбивая их
на квадратные сантиметры.- Умножь длину каждого прямоугольника на его ширину. Что получилось?
Слайд 384 этап. Сложение и вычитание величин, выраженных в единицах одного
наименования.
Например: площадь квадрата 14 см2 , а площадь прямоугольника на
26 см2 большеНайти площадь прямоугольника
14 см2+26 см2
5 этап. Введение других единиц измерения величины. Перевод из одной единицы в другую.
Слайд 406 этап. Сложение и вычитание величин, выраженных в единицах двух
наименований.
устные и письменные вычисления
а) устные вычисления. - в строчку:
5км2 46м2+
3м213см2=5 км2 49м2 213 см2б) письменные вычисления - с предварительным переводом в более мелкие меры
29га 15 а -15 га57а
2915
- 1557
________ 13га58а
1358
7 этап. Умножение и деление величины на число.
Рассматривают 2 случая: 1825
а) устные; *
13га5а*9=121га5а 6
б) письменные. ___________
18га25а*6= 10950
109га50а
Слайд 41Площадь фигуры
(Демидова, козлова, Тонких)
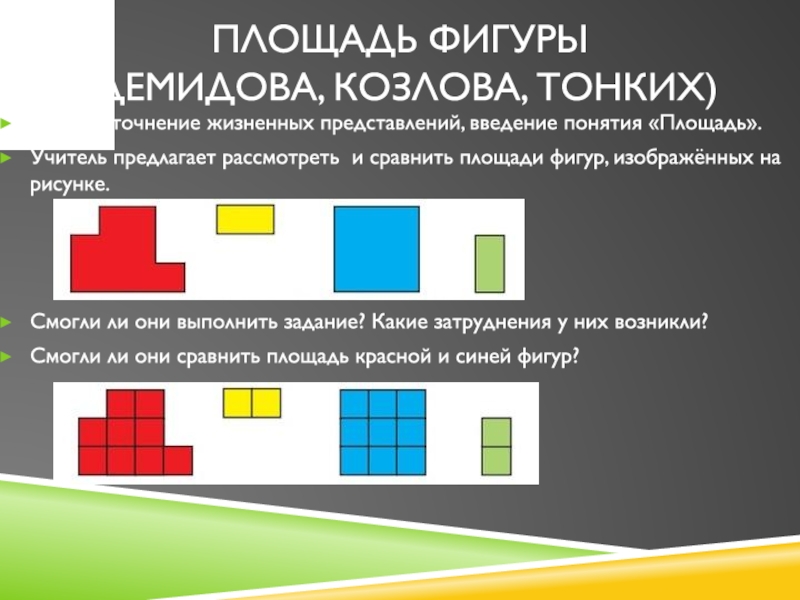
1 этап. Уточнение жизненных представлений, введение
понятия «Площадь».
Учитель предлагает рассмотреть и сравнить площади фигур, изображённых на
рисунке.Смогли ли они выполнить задание? Какие затруднения у них возникли?
Смогли ли они сравнить площадь красной и синей фигур?
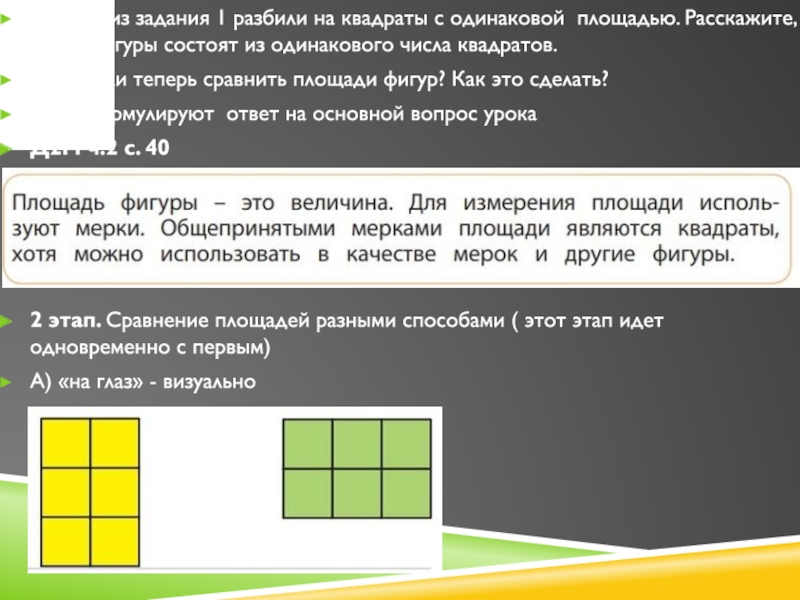
Слайд 42Фигуры из задания 1 разбили на квадраты с одинаковой площадью.
Расскажите, какие фигуры состоят из одинакового числа квадратов.
Можно ли теперь
сравнить площади фигур? Как это сделать?Дети формулируют ответ на основной вопрос урока
Д2М ч.2 с. 40
2 этап. Сравнение площадей разными способами ( этот этап идет одновременно с первым)
А) «на глаз» - визуально
Слайд 43Дети сравнивают площади фигур
Б) Сравнение способом наложения .
Сформулировать ответ на
основной вопрос урока
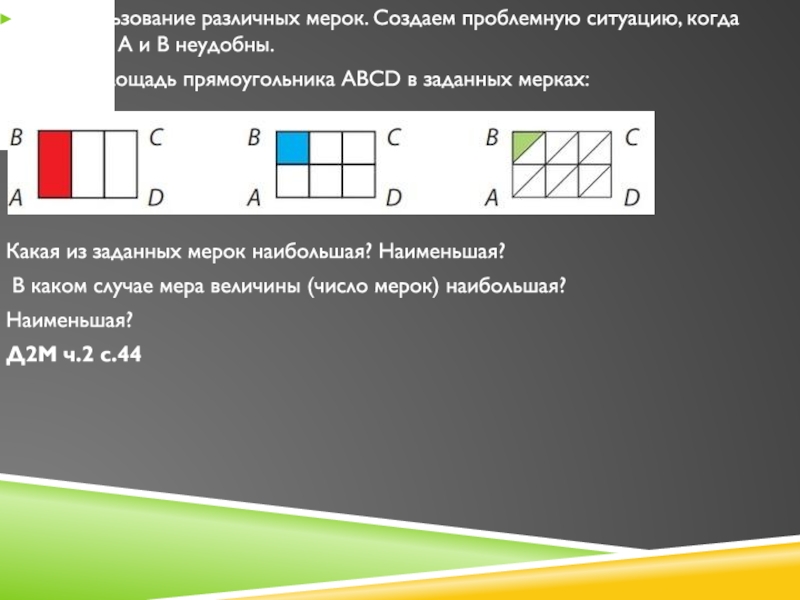
Слайд 44В) использование различных мерок. Создаем проблемную ситуацию, когда способы А
и В неудобны.
Найдите площадь прямоугольника ABCD в заданных мерках:
Какая из
заданных мерок наибольшая? Наименьшая?В каком случае мера величины (число мерок) наибольшая?
Наименьшая?
Д2М ч.2 с.44
Слайд 463 этап. Введение единой меры ( единицы измерения) площади.
Как узнать,
сколько квадратных метров в одном квадратном километре?
Сколько квадратных миллиметров в
одном квадратном сантиметре?Сформулируйте ответ на основной вопрос урока
Д4М ч.1 с.90
Слайд 48Вводим палетку. Это прозрачная пленка, расчерченная на см2. Кладем ее
на фигуру и считаем см2
Д4М ч.2 с.2
Пример:
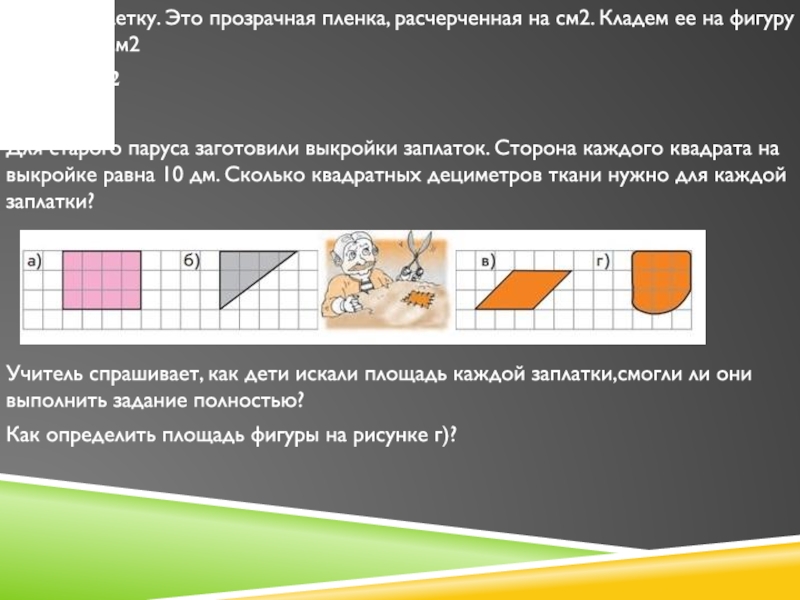
Для старого паруса заготовили
выкройки заплаток. Сторона каждого квадрата на выкройке равна 10 дм. Сколько квадратных дециметров ткани нужно для каждой заплатки?Учитель спрашивает, как дети искали площадь каждой заплатки,смогли ли они выполнить задание полностью?
Как определить площадь фигуры на рисунке г)?
Слайд 504 этап. Сложение и вычитание величин, выраженных в единицах одного
наименования.
Д2М ч.2 с.46
Например,
Площадь фигуры 16 дм2. Часть, площадью 6
дм2 закрашена зеленым цветом. Сколько дм2 закрашено голубым цветом?16дм2-6дм2=10 дм2
5 этап. Введение других единиц измерения величины. Перевод из одной единицы в другую.
Д4М ч.1 с.92
Учитель просит выписать величины в порядке возрастания.
Площадь посёлка Кашино – один квадратный километр, площадь
картофельного поля за посёлком – один гектар, а детская площадка
в центре Кашино занимает один ар.
Слайд 51Учитель спрашивает, смогли ли они выполнить задание? Все ли названные
в нём единицы измерения площади им известны?
Слайд 526 этап. Сложение и вычитание величин, выраженных в единицах двух
наименований.
Дети выполняют устные и письменные вычисления
а) устные вычисления. - в
строчку:20дм2-16дм2=4дм2
б) письменные вычисления - с предварительным переводом в более мелкие меры
35га 16 а -30га25а
3516
- Ответ:4га91а
3025
_________
491
Слайд 537 этап. Умножение и деление величины на число.
Рассматривают 2 случая:
а)
устные;
21га5а*5=107га5а
б) письменные
4 км2 750м2 * 5 = 23км2 750м2
4750*
5
___________
23750