Слайд 1Множества и операции над ними
1. Понятие множества и элемента множества.
2. Способы задания множеств. Отношения между множествами и их свойства.
3. Операция пересечения множеств. Свойства пересечения.
4. Операция объединения множеств. Свойства объединения.
5. Вычитание множеств. Дополнение. Свойства вычитания множеств
6. Классификация
7. Декартово произведение множеств
Слайд 2Множества
Понятие множества является одним из основных понятий математики и
поэтому не определяется через другие.
Обозначение:
А, В, С -
множества;
а, b, с - элементы множества
аА -объект а принадлежит множеству А;
аА -объект а не принадлежит множеству А.
Множество, не содержащее никаких элементов, называют пустым и обозначают .
Множества бывают конечными и бесконечными.
Слайд 3Способы задания множеств
Множество задано, если о любом объекте можно сказать,
принадлежит он этому множеству или не принадлежит.
Способы задания множества:
1. Перечисление
всех элементов множества.
Например, А ={2, 4, 6, 8 }.
2. Указание характеристического свойства элементов, т.е. такого свойства, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
Например, А ={ х х N и х 175}
Слайд 4Отношения между множествами
Если множества A и B имеют общие элементы,
т.е. элементы, принадлежащие одновременно A и B, то говорят, что
эти множества пересекаются.
Если множества A и B не имеют общих элементов, т.е. нет элементов, принадлежащих одновременно A и B, то говорят, что эти множества не пересекаются.
Множество В называется подмножеством множества А, если каждый элемент множества В является также элементом множества А. (В А)
Пустое множество считают подмножеством любого множества. ( А )
Любое множество является подмножеством самого себя. (А А )
Если число элементов множества B равно n, то число различных подмножеств данного множества 2n.
Множества А и В называются равными, если А В и В А. (А=В)
Задача. В каком отношении находятся множества А= {1,2, 3, 4,5} , В= {1,5,7, 9 }, C= {7, 9} D= {7, 9, 5, 1} ?
Слайд 5Круги Эйлера
Отношения между множествами наглядно представляют с помощью особых чертежей,
кругов Эйлера.
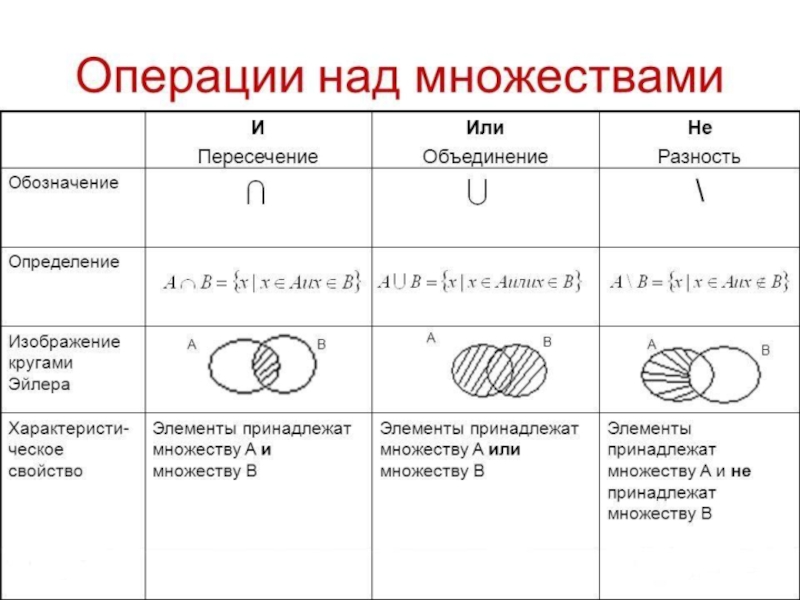
Слайд 7Пересечение множеств
Пересечением множеств А и В называется множество, состоящее из
тех и только тех элементов, которые принадлежат как множеству А,
так и множеству В. (обоз. A B )
A B = {x | x A и x B}.
Пересечение любых множеств А и В всегда существует, и оно единственно.
Когда множества А и В не имеют общих элементов, то говорят, что их пересечение пусто ( АВ= ).
Операция, при помощи которой находят пересечение множеств, называется также пересечением.
Слайд 8Свойства пересечения множеств
1)А=;
2) АА=А;
3)АВ=ВА; - коммутативность операции пересечения
4) А
(ВС) = (АВ) С=АВС; - ассоциативность операции пересечения
5)
АВ АВ=А;
Слайд 9Объединение множеств
Объединением множеств А и В называется множество, состоящее из
тех и только тех элементов, которые принадлежат хотя бы одному
из множеств А и В. (обоз. A B )
A B = {х | х A или х B}.
Объединение любых множеств А и В всегда существует, и оно единственно.
Операция, при помощи которой находят объединение множеств, называется также объединением.
Слайд 10Свойства объединения множеств
1. AU=A;
2.AA=A;
3. AUB=BUA;
4. А (ВС) = (АВ)
С=АВС;
5. АВ АВ=В;
Слайд 11Свойства, связывающие операции пересечения и объединения множеств
А(ВА)=А.
A(BUA)=A.
AU(BC)=(AUB)(AUC).
A(BUC)=(AB)U(AC).
Если
в выражении есть знаки пересечения и объединения множеств и нет
скобок, то сначала выполняют пересечение, так как считают, что пересечение более «сильная» операция, чем объединение.
Слайд 12Вычитание множеств
Разностью множеств A и B называется множество, содержащее те
и только те элементы, которые принадлежат множеству A и не
принадлежат множеству B. (обоз. A \ B).
A \ B = {x | x A и x B}.
Операция, при помощи которой находят разность множеств, называется вычитанием.
Если A B= , A \ B = A
Если A B, A \ B =
Слайд 13Дополнение множеств
Пусть B A. Дополнением множества B до множества
A называется множество, содержащее те и только те элементы множества
A, которые не принадлежат множеству B. (обоз.BA)
B A, A\B = BA
Задача. Пусть A = {1, 2, 3, 4, 5}, а B = {2, 4}. Найдите BA.
Слайд 14Порядок выполнения действий в выражениях
Условились считать, что пересечение – более «сильная»
операция, чем вычитание. Объединение и вычитание множеств считают равноправными.
Задача. Расставьте
порядок действий в выражении A \ B C D.
Слайд 15Свойства вычитания множеств
1. (A \ B) \ C = (A
\ C) \ B;
2. (A B) \ C =
(A \ C) (B \ C);
3. (A \ B) C = (A C) \ (B C);
4. A \ (B C) = (A \ B) (A \ C);
5. A \ (B C) = (A \ B) (A \ C).
Слайд 16Разбиение множества на классы
Множество X разбито на классы X1, X2,
..., Xn, если:
1) подмножества X1, X2, ..., Xn попарно не
пересекаются;
2) объединение подмножеств X1, X2, ..., Xn совпадает с множеством X.
Пример правильной классификации: множество Х треугольников разбили на классы остроугольных, тупоугольных, прямоугольных.
Пример неправильной классификации: множество X треугольников разбили на классы равнобедренных, равносторонних и разносторонних треугольников
Слайд 17Дихотомическая классификация
Так как разбиение множества на классы связано с
выделением его подмножеств, то классификацию можно выполнять при помощи свойств
элементов множеств.
Вообще, если на множестве X задано одно свойство, то это множество разбивается на два класса. Первый – это класс объектов, обладающих этим свойством, а второй – дополнение первого класса до множества X. Во втором классе содержатся такие объекты множества X, которые заданным свойством не обладают. Такую классификацию называют дихотомической.
Слайд 18Задача 1. Составьте слоги, состоящие из двух букв, из которых
первая — любая согласная из П, Р, С, а вторая
— любая гласная из А, У?
С={П, Р, С} и V = {А, У}
S={(П; A), (П; У), (Р; A), (Р; У), (С; A), (С; У)}
Задача 2. Составьте слоги, состоящие из двух букв, из которых первая — любая гласная из А, У, а вторая — любая согласная из П, Р, С?
С={П, Р, С} и V = {А, У}
М={(А; П), (У; П), (А; Р), (У; Р), (А; С), (У; С)}
Слайд 19Декартово произведение множеств
Декартовым произведением множеств А и В называется множество
всех пар, первая компонента которых принадлежит множеству А, а вторая
принадлежит множеству В. (обоз. A х B )
А х В = {(х; у) хА и уВ}.
Если какое-либо из множества А и В пусто, то декартово произведение А х В считается пустым множеством.
Слайд 20Кортежи
Упорядоченные наборы называют кортежами и различают по длине. Длина кортежа –
это число элементов, из которых он состоит.
Например, (3; 6;
7) – это кортеж длины 3, (м, а, т, е, м, а, т, и, к, а) – это кортеж длины 10.
Слайд 21Декартово произведение n множеств
Декартовым произведением множеств A1, A2, ... ,
An называется множество всех кортежей длины n, первая компонента которых
принадлежит множеству A1, вторая – множеству A2, ..., n-я – множеству An. (A1 A2 ... An).
Слайд 22Свойства декартова произведения множеств
А х В В х
А
(А х В) х С А х
(В х С )
1. (АВ) х С = (АхС) (ВхС)
2. (А\В) х С = (АхС) \ (ВхС)
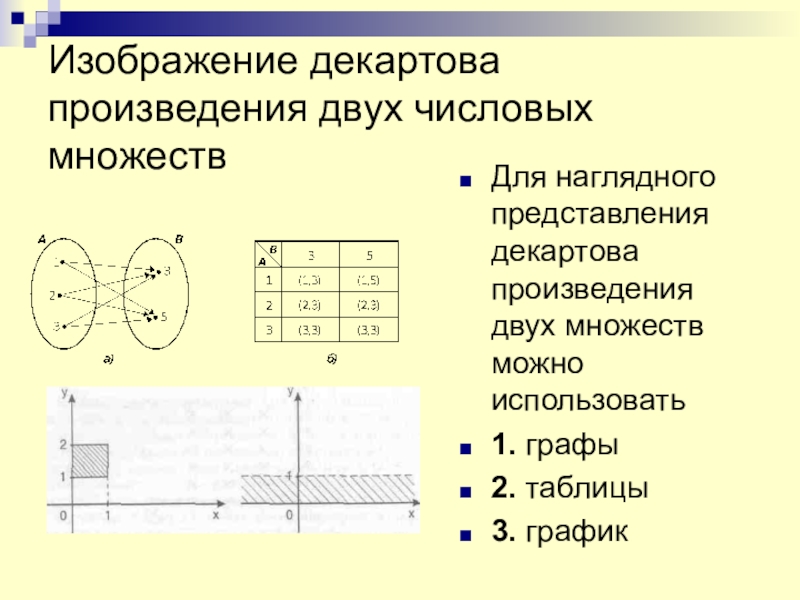
Слайд 23Изображение декартова произведения двух числовых множеств
Для наглядного представления декартова произведения
двух множеств можно использовать
1. графы
2. таблицы
3. график
Слайд 24Число элементов в объединении, разности и декартовом произведении конечных множеств
n(A)
= a - множество A содержит a элементов
n(A B)
= n(A) + n(B) = a + b, если А и В не пересекаются
n(A1 A2 ... At) = n(A1) + n(A2) + ... + n(At), если множества попарно не пересекаются
n(A B) = n(A) + n(B) – n(A B), если А и В пересекаются
Если B A, то n(BA) = n(A) – n(B)
n(A B) = n(A)n(B) = аb
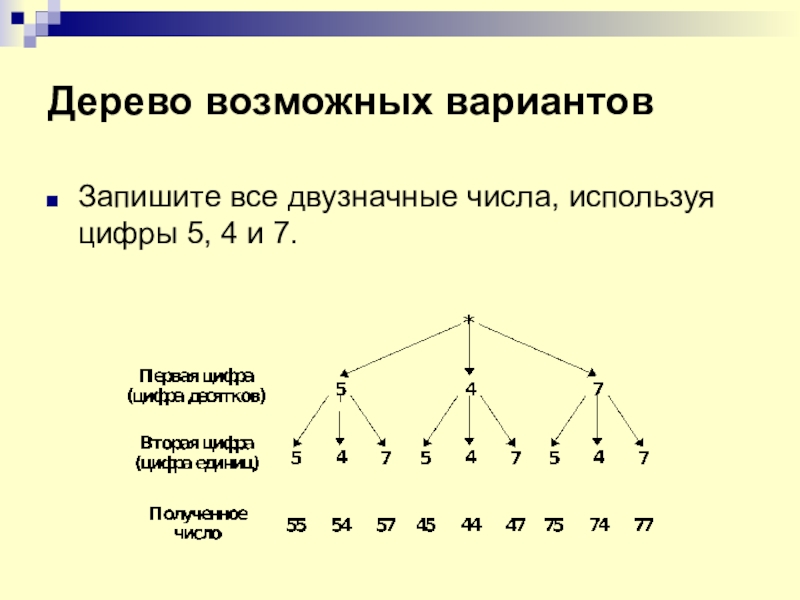
Слайд 25Дерево возможных вариантов
Запишите все двузначные числа, используя цифры 5, 4
и 7.