Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МОДЕЛЬ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Содержание
- 1. МОДЕЛЬ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
- 2. Пример: Множественная регрессияМы хотим определить связь между
- 3. МОДЕЛЬ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИДля оценки необходима выборка (большое количество семей)
- 4. доходы i-й семьиn – объем выборкипотребительские расходы i-й семьи доход i-й семьи размер i-й семьи
- 5. Чтобы подобрать наилучшие
- 6. Модель строим с помощью Сервис – Анализ
- 7. Модель строим с помощью Сервис – Анализ
- 8. ИНТЕРПРЕТАЦИЯ ПАРАМЕТРОВ ЛИНЕЙНОЙ МНОЖЕСТВЕННОЙ РЕГРЕССИИИнтерпретация: коэффициент регрессии
- 9. Модель строим с помощью Сервис – Анализ
- 10. Модель строим с помощью Сервис – Анализ
- 11. Сравнение влияния на зависимую переменную различных объясняющих
- 12. Сравнение влияния на зависимую переменную различных объясняющих
- 13. Как оценить качество построенной модели?Вычисляем прогноз по моделиB=57.34-0.938P+9.892YD
- 14. Как оценить качество построенной модели?Вычисляем остатки
- 15. Как оценить качество построенной модели?Находим относительную ошибку аппроксимацииПроцентный формат
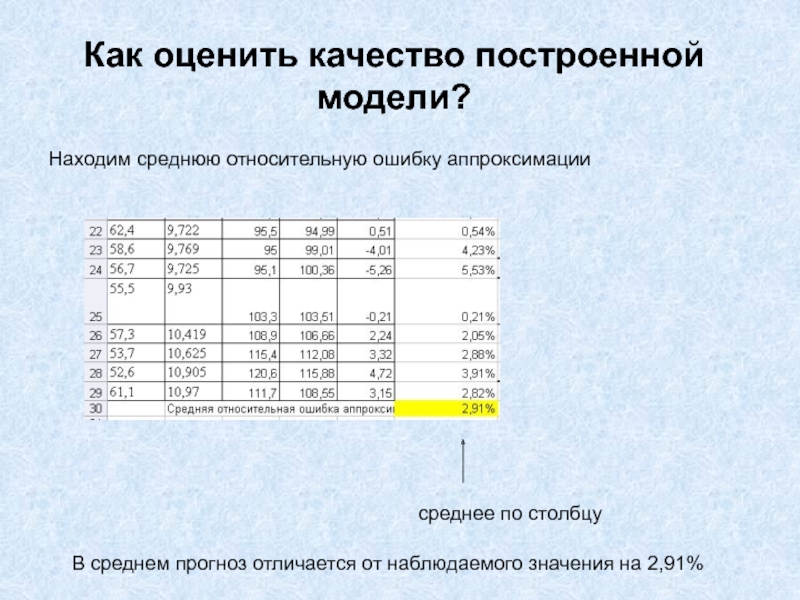
- 16. Как оценить качество построенной модели?Находим среднюю относительную
- 17. Как оценить качество построенной модели?Еще один показатель
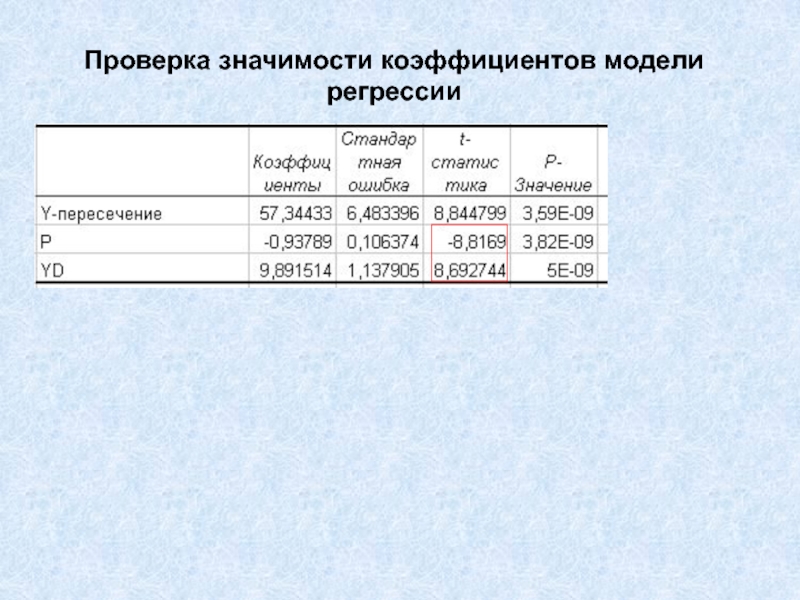
- 18. Проверка значимости коэффициентов модели регрессииПостроено уравнение Необходимо
- 19. Проверка значимости коэффициентов модели регрессииПостроено уравнение Необходимо
- 20. Проверка значимости коэффициентов модели регрессии
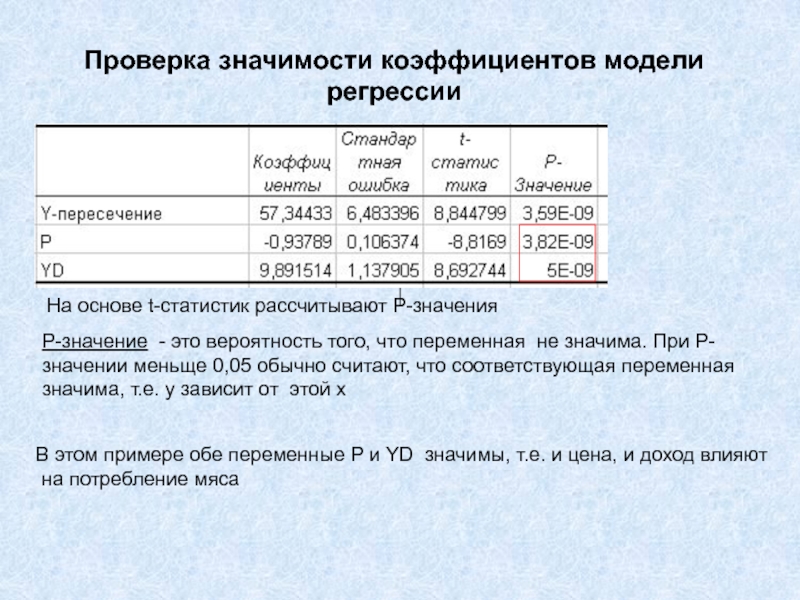
- 21. Проверка значимости коэффициентов модели регрессииР-значение - это
- 22. Проверка значимости уравнения регрессии в целомУравнение регрессии
- 23. Проверка значимости уравнения регрессии в целомУравнение регрессии
- 24. Проверка значимости уравнения регрессии в целомУравнение регрессии
- 25. Модели множественной нелинейной регрессииПостроим теперь степенную модель зависимости потребления мяса от цены и дохода:
- 26. Модели множественной нелинейной регрессииПостроим теперь степенную модель зависимости потребления мяса от цены и дохода:Прологарифмируем модель
- 27. Модели множественной нелинейной регрессииПостроим теперь степенную модель зависимости потребления мяса от цены и дохода:Прологарифмируем модель
- 28. Модели множественной нелинейной регрессииПостроим теперь степенную модель
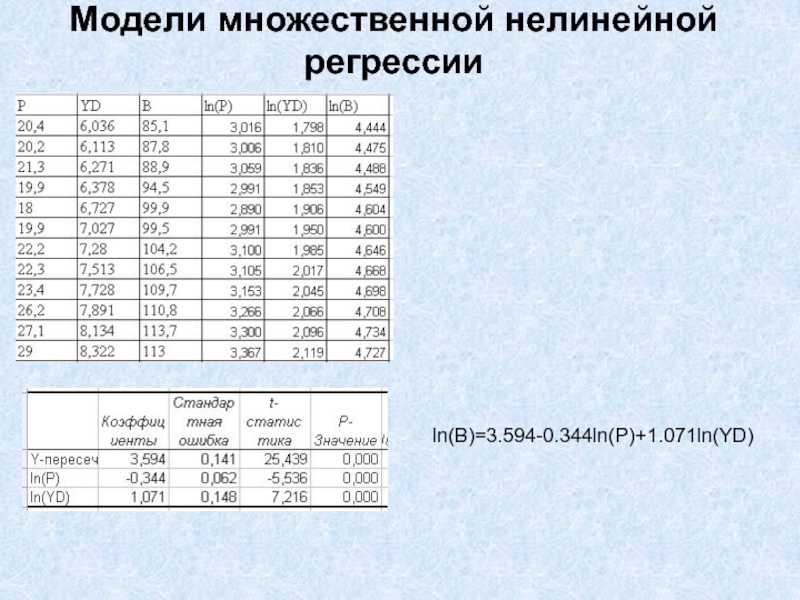
- 29. Модели множественной нелинейной регрессииln(B)=3.594-0.344ln(P)+1.071ln(YD)
- 30. Модели множественной нелинейной регрессииln(B)=3.594-0.344ln(P)+1.071ln(YD)
- 31. Модели множественной нелинейной регрессииln(B)=3.594-0.344ln(P)+1.071ln(YD)
- 32. Модели множественной нелинейной регрессииln(B)=3.594-0.344ln(P)+1.071ln(YD)степенная модель множественной регрессииКоэффициенты - эластичности
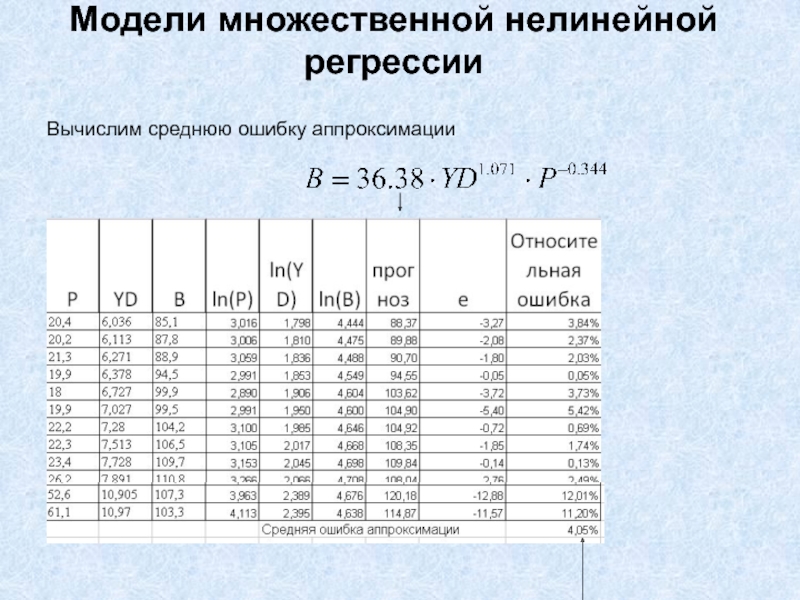
- 33. Модели множественной нелинейной регрессииВычислим среднюю ошибку аппроксимации
- 34. Скачать презентанцию
Пример: Множественная регрессияМы хотим определить связь между потреблением, доходом семьи, финансовыми активами семьи и размером семьи.y – потребительские расходы.x1 – доход семьи x2 – финансовые активы семьи x3 – размер семьи
Слайды и текст этой презентации
Слайд 1МОДЕЛЬ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
В модели множественной регрессии переменная y зависит
от нескольких
Слайд 2Пример:
Множественная регрессия
Мы хотим определить связь между потреблением, доходом семьи, финансовыми
активами семьи и размером семьи.
y – потребительские расходы.
x1 – доход
семьи x2 – финансовые активы семьи
x3 – размер семьи
Слайд 3МОДЕЛЬ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Для оценки необходима выборка (большое количество семей)
Слайд 4доходы i-й семьи
n – объем выборки
потребительские расходы i-й семьи
доход
i-й семьи
размер i-й семьи
Слайд 6Модель строим с помощью Сервис – Анализ данных - регрессия
Пример:
Имеются данные о потреблении мяса в США B в 1980
– 2007 годах(фунты на душу населения), и его зависимости от цены P (центы за фунт) и
личного располагаемого дохода YD (тысячи долларов в расчете на душу
населения).
Построим модель зависимости потребления мяса от цены и дохода
Слайд 7Модель строим с помощью Сервис – Анализ данных - регрессия
Пример:
Имеются данные о потреблении мяса в США B в 1980
– 2007 годах(фунты на душу населения), и его зависимости от цены P (центы за фунт) и
личного располагаемого дохода YD (тысячи долларов в расчете на душу
населения).
Построим модель зависимости потребления мяса от цены и дохода
B=57.34-0.938P+9.892YD
Слайд 8ИНТЕРПРЕТАЦИЯ ПАРАМЕТРОВ ЛИНЕЙНОЙ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Интерпретация: коэффициент регрессии при переменной xi
показывает на сколько единиц изменится переменная y при изменении переменной
xi на 1 единицу, при условии постоянства других переменных:
Слайд 9Модель строим с помощью Сервис – Анализ данных - регрессия
Пример:
Имеются данные о потреблении мяса в США B в 1980
– 2007 годах(фунты на душу населения), и его зависимости от цены P (центы за фунт) и
личного располагаемого дохода YD (тысячи долларов в расчете на душу
населения).
Построим модель зависимости потребления мяса от цены и дохода
B=57.34-0.938P+9.892YD
При увеличении цены на мясо на 1 цент за фунт потребление сократится на
0,938 фунтов на душу населения
Слайд 10Модель строим с помощью Сервис – Анализ данных - регрессия
Пример:
Имеются данные о потреблении мяса в США B в 1980
– 2007 годах(фунты на душу населения), и его зависимости от цены P (центы за фунт) и
личного располагаемого дохода YD (тысячи долларов в расчете на душу
населения).
Построим модель зависимости потребления мяса от цены и дохода
B=57.34-0.938P+9.892YD
Какой фактор цена или доход влияет сильнее на потребление мяса?
Слайд 11Сравнение влияния на зависимую переменную различных объясняющих переменных
Средняя эластичность по
цене. Показывает на сколько % изменится потребление мяса, если цена
увеличится на 1% процент.Расчет средних эластичностей
Слайд 12Сравнение влияния на зависимую переменную различных объясняющих переменных
Средняя эластичность по
доходу. Показывает на сколько % изменится потребление мяса, если доход
увеличится на 1% процент.Расчет средних эластичностей
Чем больше эластичность по абсолютной величине, тем сильнее влияние
Слайд 15Как оценить качество построенной модели?
Находим относительную ошибку аппроксимации
Процентный формат
Слайд 16Как оценить качество построенной модели?
Находим среднюю относительную ошибку аппроксимации
среднее по
столбцу
В среднем прогноз отличается от наблюдаемого значения на 2,91%
Слайд 17Как оценить качество построенной модели?
Еще один показатель качества – коэффициент
детерминации. Он
показывает долю вариации зависимой переменной, объясненную
включенными в
модель факторами.76,4% вариации потребления мяса объясняется ценой и доходом.
Слайд 18Проверка значимости коэффициентов модели регрессии
Построено уравнение
Необходимо проверить значимость коэффициентов
а и b
Если коэффициент a незначим, то потребление мяса
не зависитот цены. Если коэффициент b незначим, то потребление мяса не зависит от
дохода
Слайд 19Проверка значимости коэффициентов модели регрессии
Построено уравнение
Необходимо проверить значимость коэффициентов
а и b
Если коэффициент a незначим, то потребление мяса
не зависитот цены. Если коэффициент b незначим, то потребление мяса не зависит от
дохода
Для проверки значимости коэффициентов рассчитываются величины T
Слайд 21Проверка значимости коэффициентов модели регрессии
Р-значение - это вероятность того, что
переменная не значима. При Р-значении меньще 0,05 обычно считают, что
соответствующая переменная значима, т.е. y зависит от этой хВ этом примере обе переменные P и YD значимы, т.е. и цена, и доход влияют
на потребление мяса
На основе t-статистик рассчитывают Р-значения
Слайд 22Проверка значимости уравнения регрессии в целом
Уравнение регрессии считается незначимым, если
ни одна из переменных,
включенных в уравнение не влияет на переменную
yДля проверки значимости уравнения регрессии в целом, рассчитывается
F-статистика
Слайд 23Проверка значимости уравнения регрессии в целом
Уравнение регрессии считается незначимым, если
ни одна из переменных,
включенных в уравнение не влияет на переменную
yДля проверки значимости уравнения регрессии в целом, рассчитывается
F-статистика
Значимость F показывает вероятность того, что уравнение незначимо, т.е
y не зависит от включенных в уравнение переменных х. Обычно считают,
что если Значимость F<0.05, то уравнение регрессии значимо, т.е. хотя бы
одна из включенных в уравнение переменных влияет на y.
Слайд 24Проверка значимости уравнения регрессии в целом
Уравнение регрессии считается незначимым, если
ни одна из переменных,
включенных в уравнение не влияет на переменную
yДля проверки значимости уравнения регрессии в целом, рассчитывается
F-статистика
В нашем случае уравнение регрессии значимо.
Слайд 25Модели множественной нелинейной регрессии
Построим теперь степенную модель зависимости потребления мяса
от цены и дохода:
Слайд 26Модели множественной нелинейной регрессии
Построим теперь степенную модель зависимости потребления мяса
от цены и дохода:
Прологарифмируем модель
Слайд 27Модели множественной нелинейной регрессии
Построим теперь степенную модель зависимости потребления мяса
от цены и дохода:
Прологарифмируем модель
Слайд 28Модели множественной нелинейной регрессии
Построим теперь степенную модель зависимости потребления мяса
от цены и дохода:
Прологарифмируем модель
Теперь построим линейную модель с помощью
сервиса Анализ данных, задав в качестве зависимой переменной ln(b), а в качестве регрессоров ln(YD) и ln(P)
Слайд 32Модели множественной нелинейной регрессии
ln(B)=3.594-0.344ln(P)+1.071ln(YD)
степенная модель множественной регрессии
Коэффициенты - эластичности
