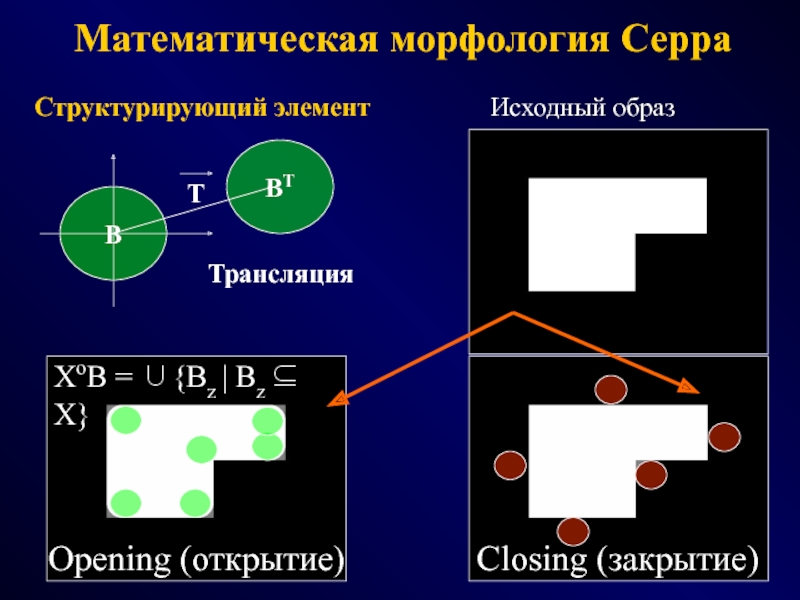
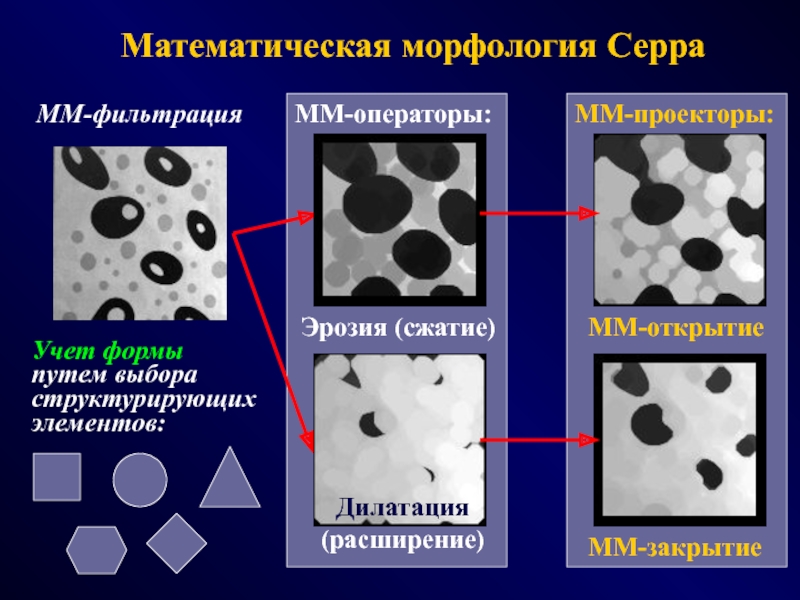
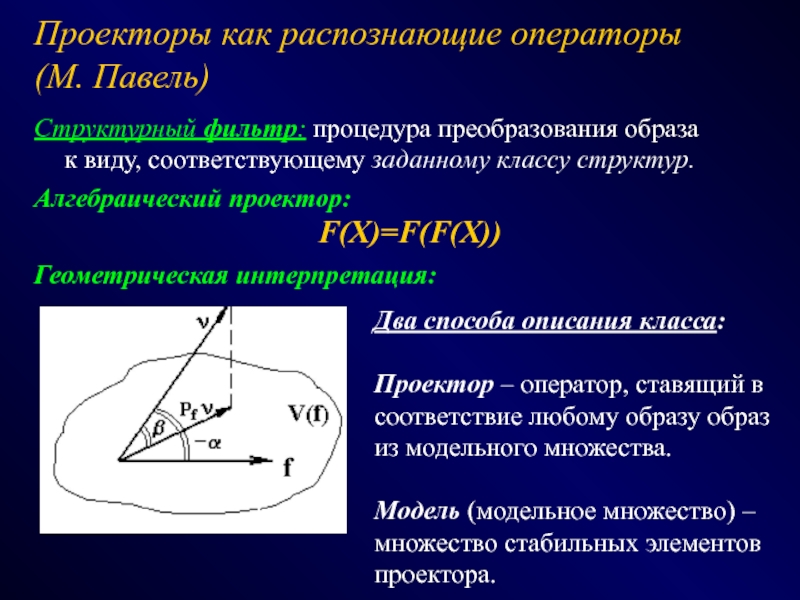
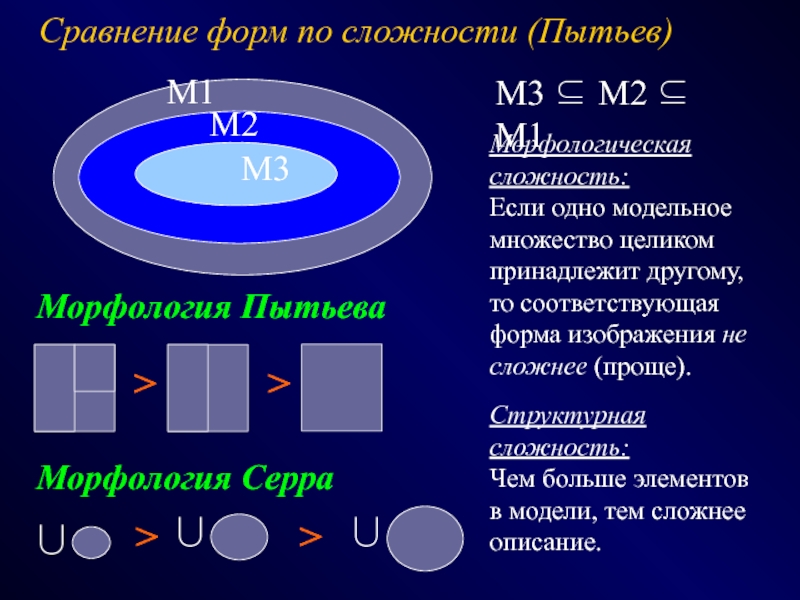
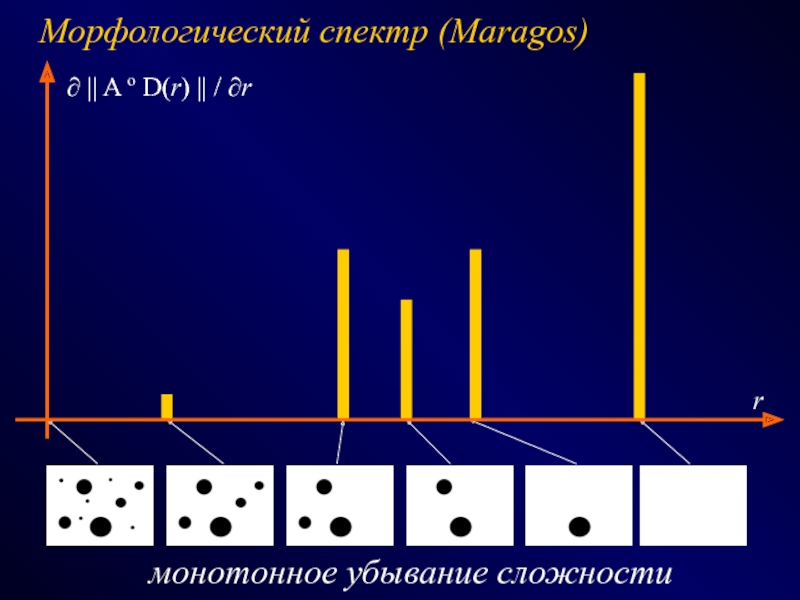
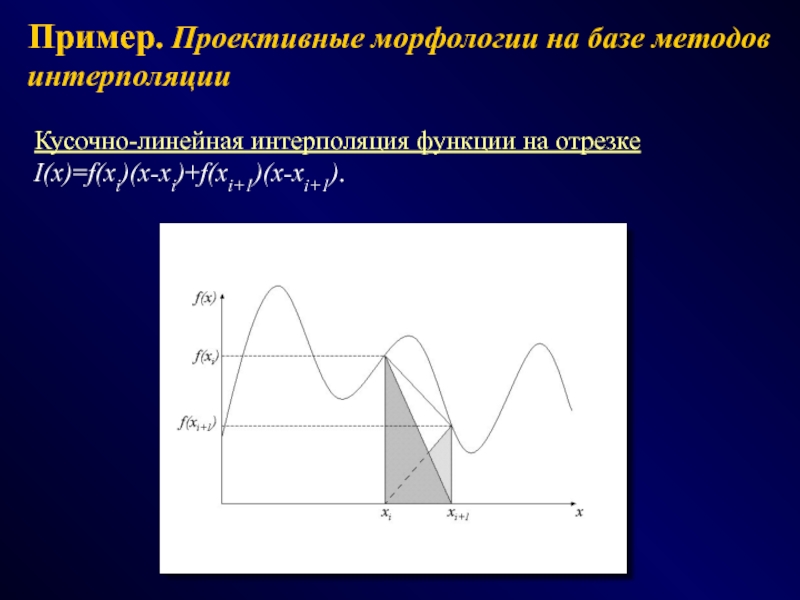
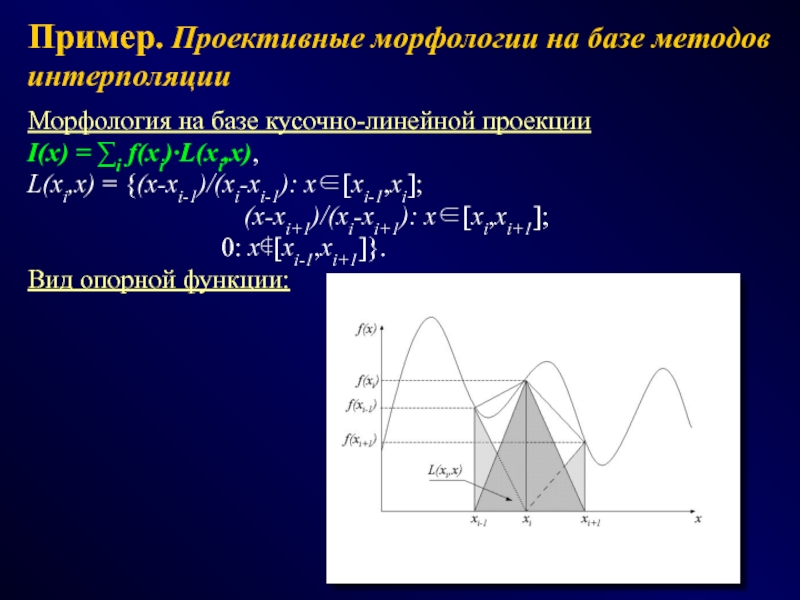
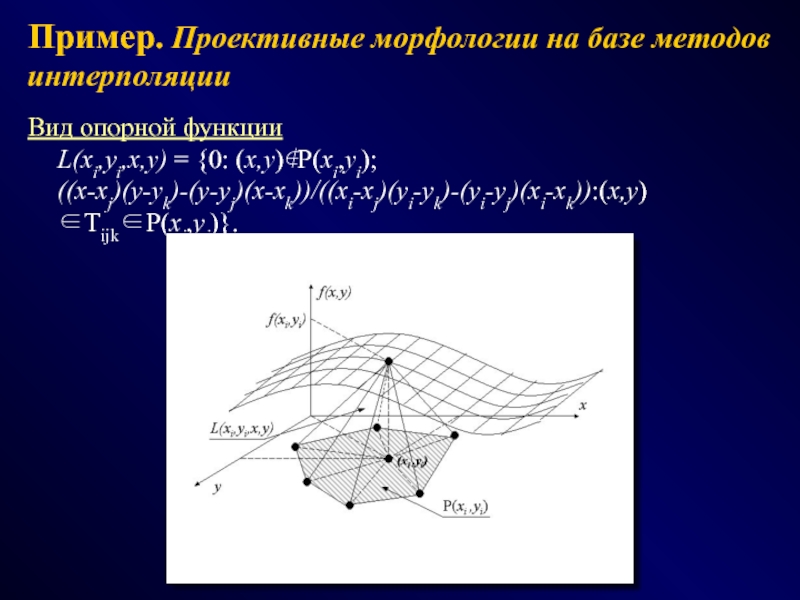
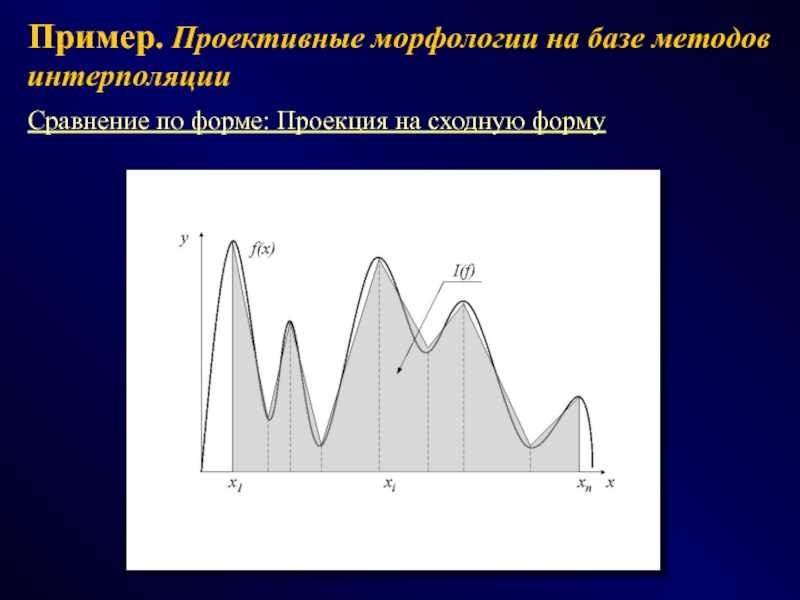
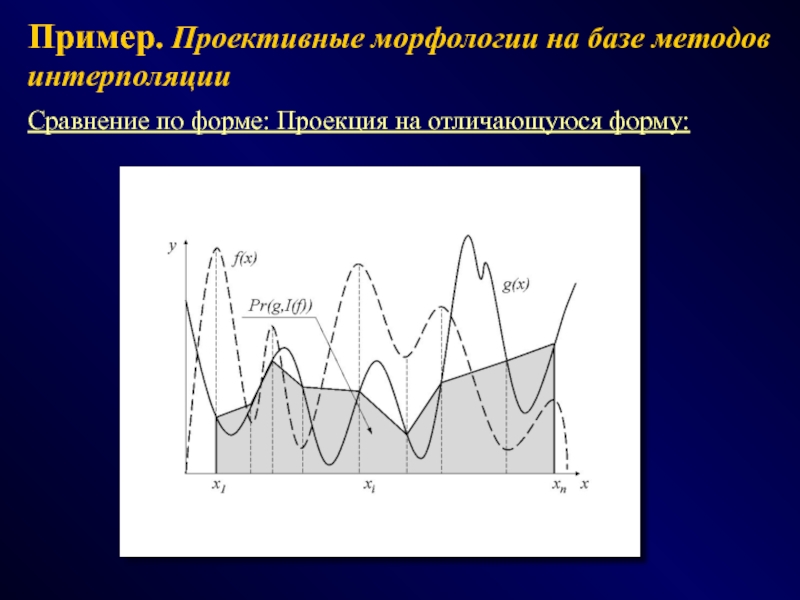
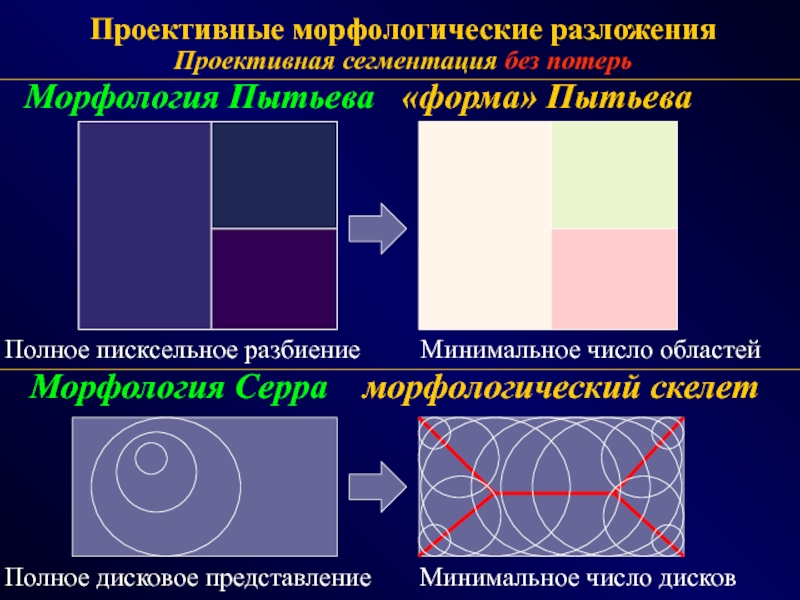
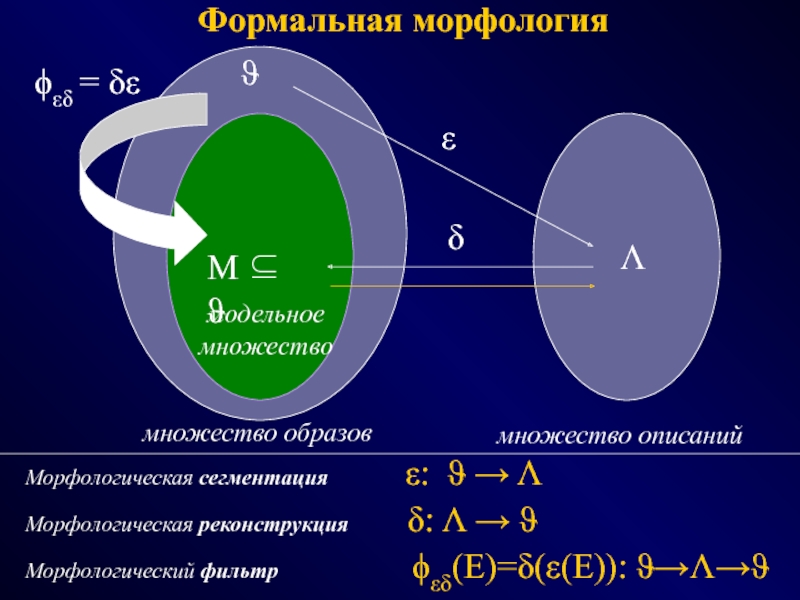
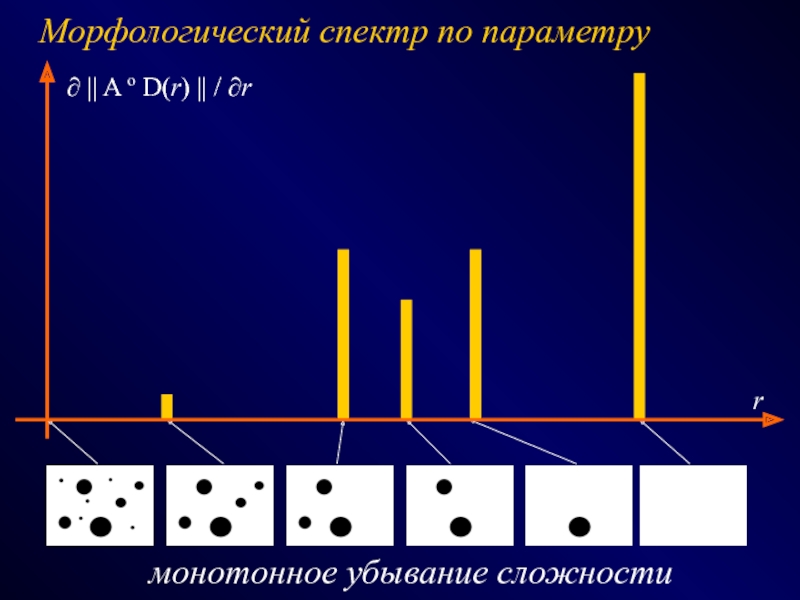
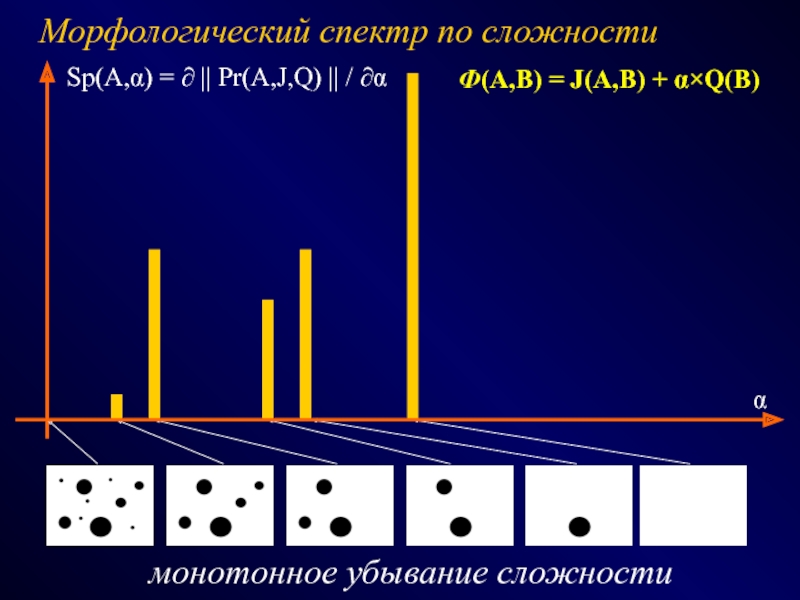
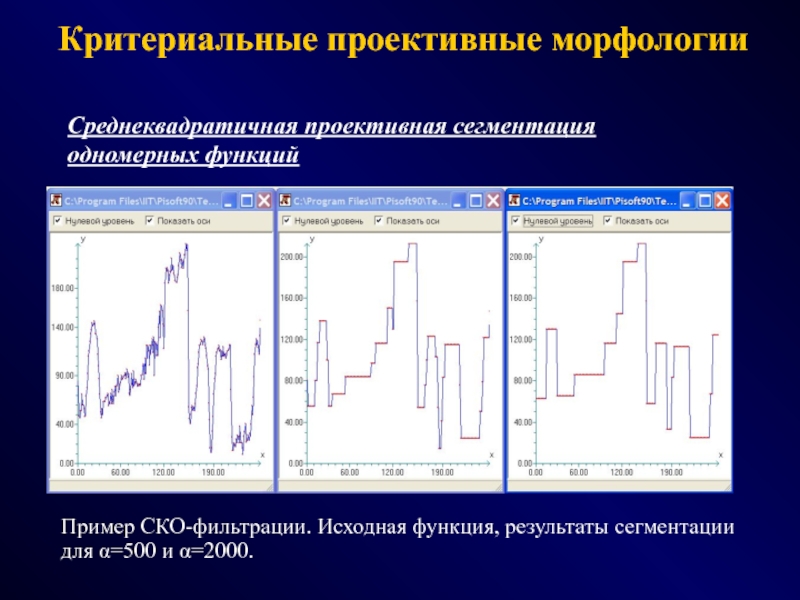
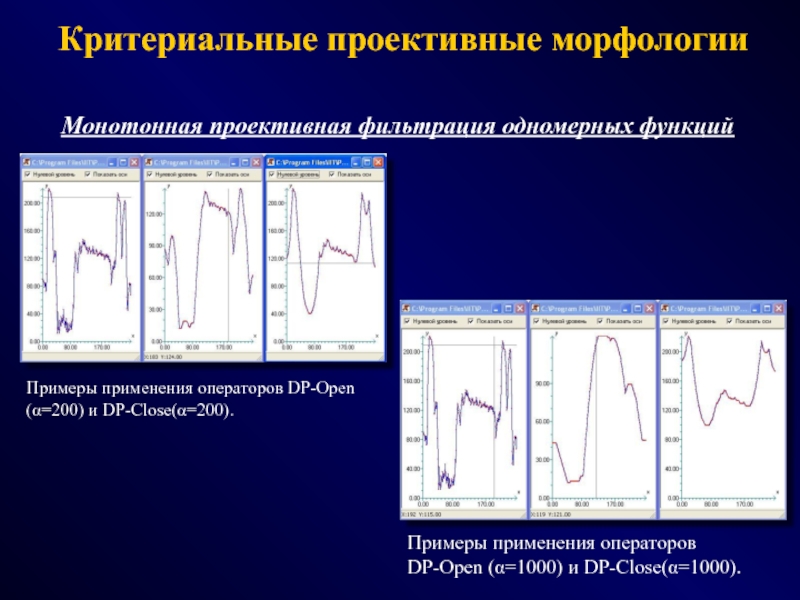
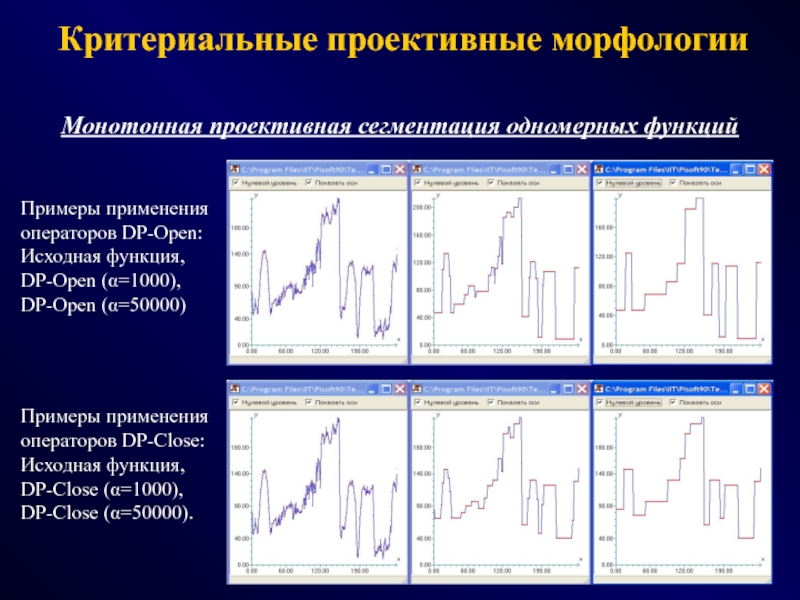
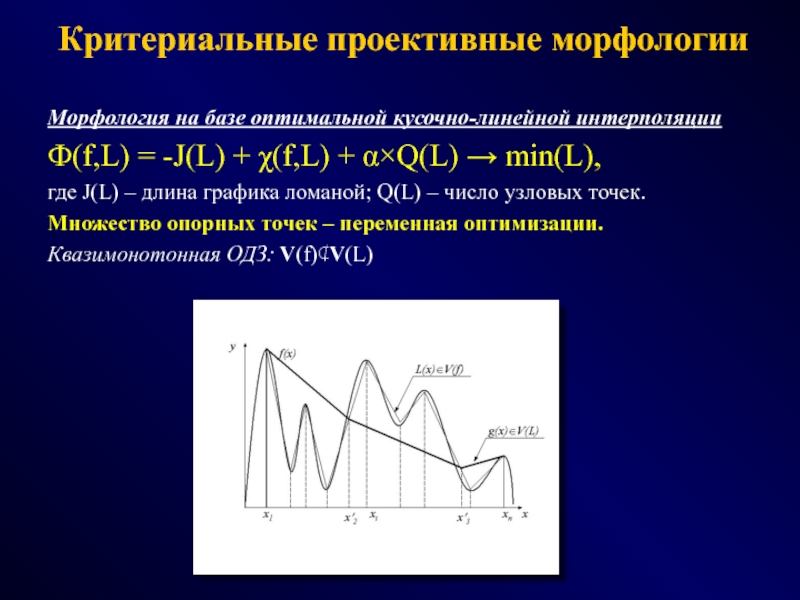
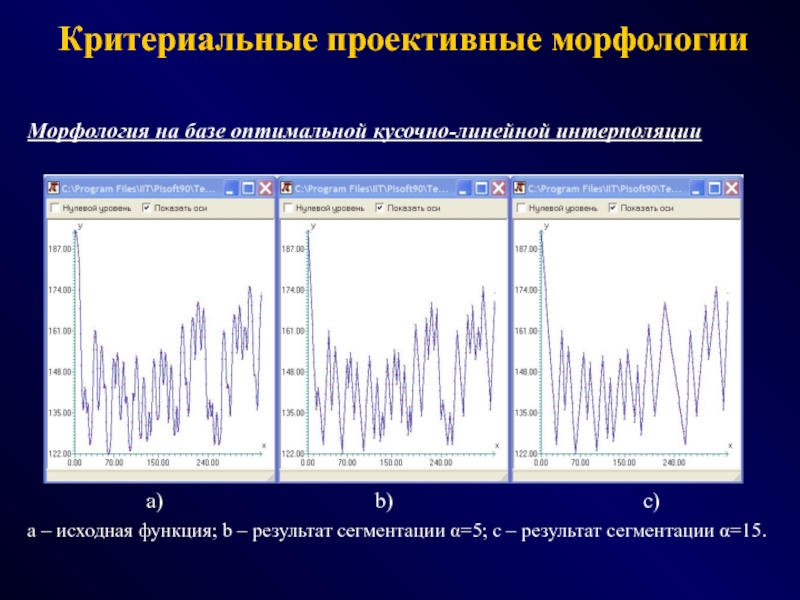
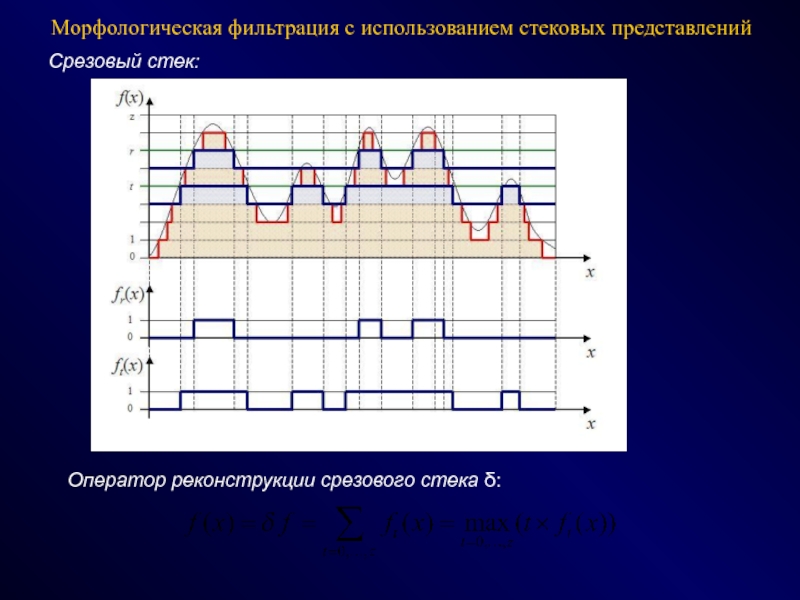
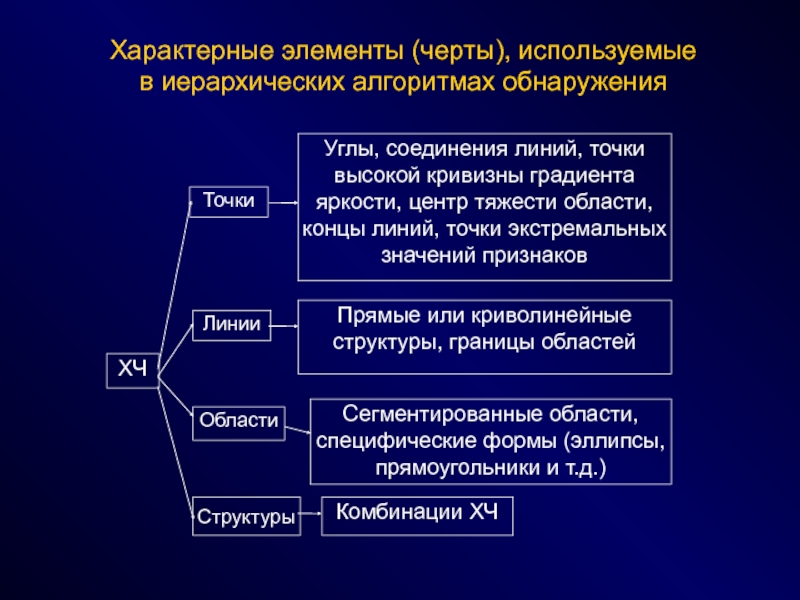
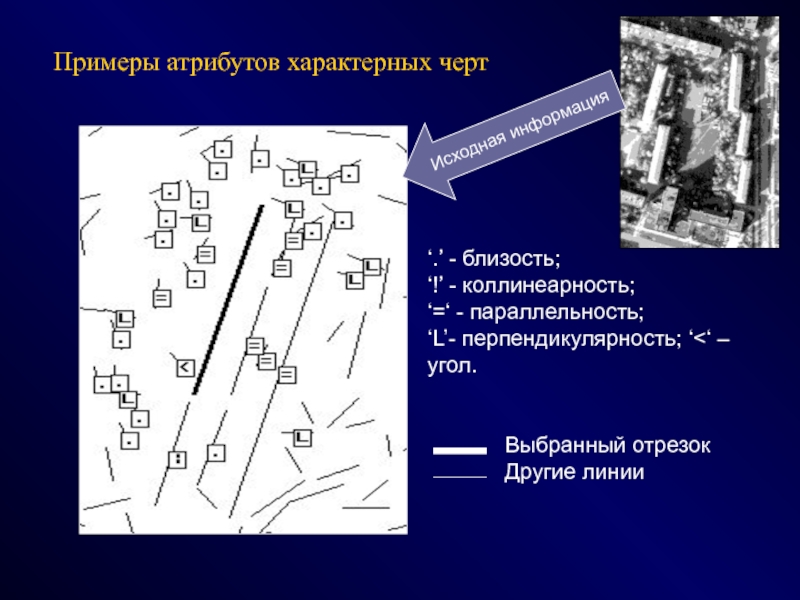
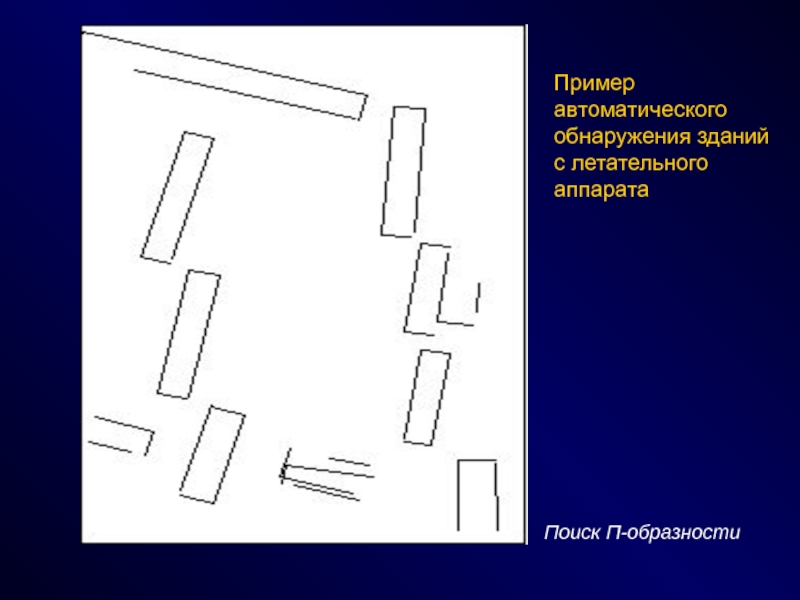
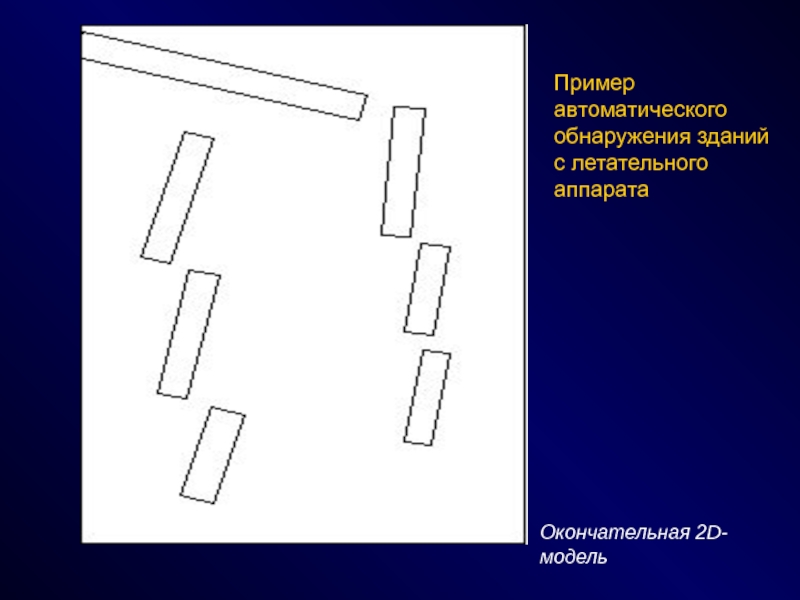
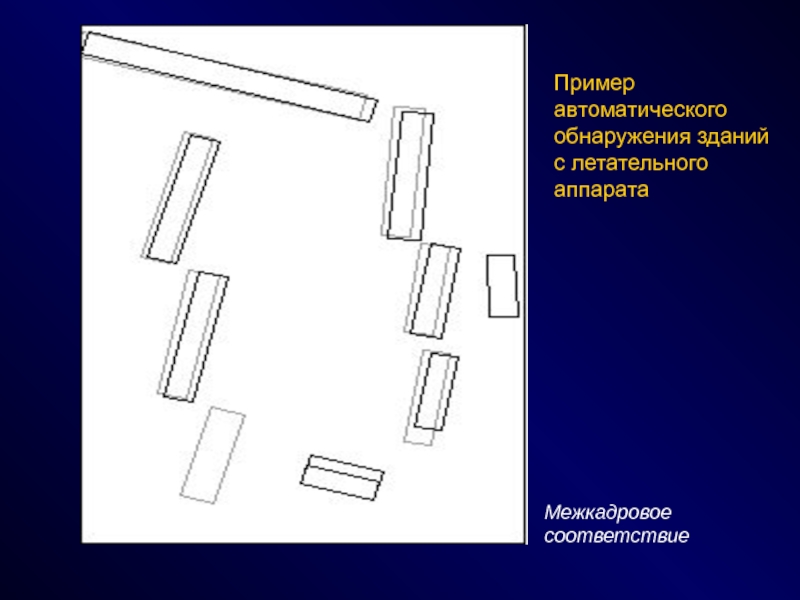
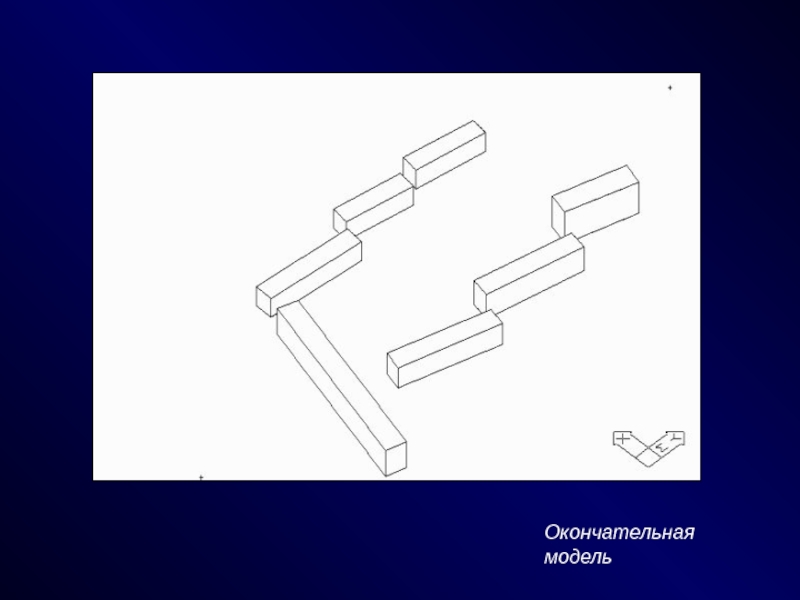
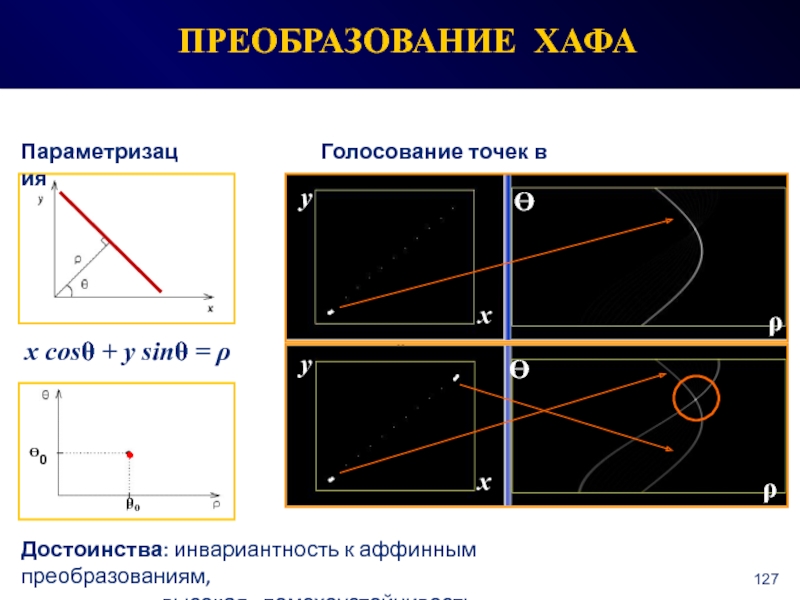
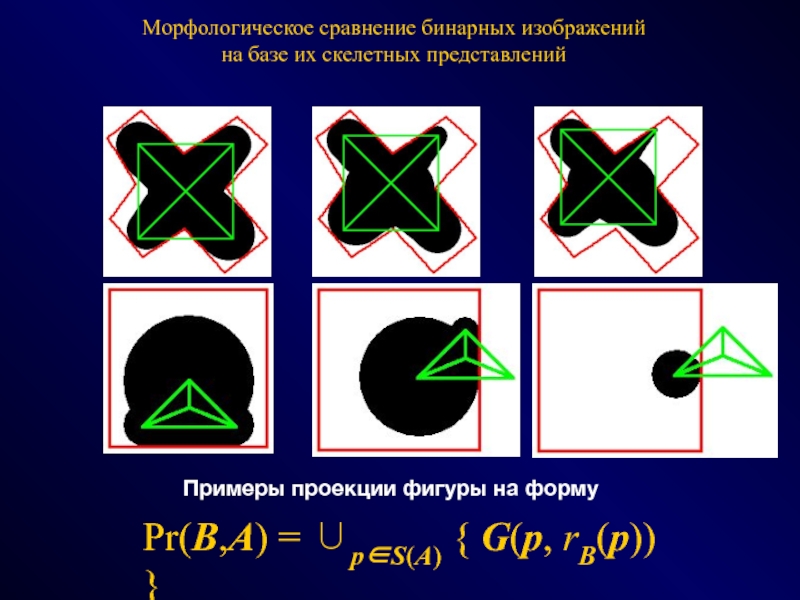
СПОСОБЫ - эвристики, эксперименты
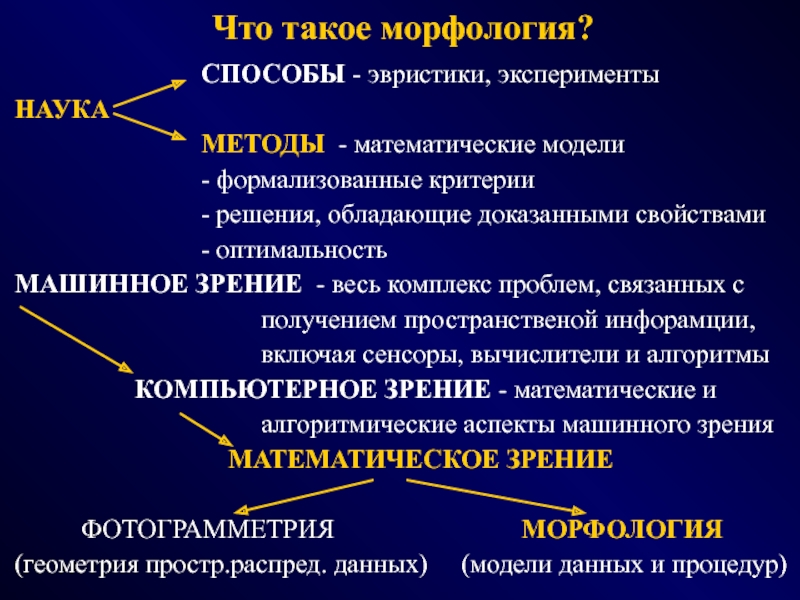
НАУКА
МЕТОДЫ - математические модели
- формализованные критерии
- решения, обладающие доказанными свойствами
- оптимальность
МАШИННОЕ ЗРЕНИЕ - весь комплекс проблем, связанных с
получением пространственой инфорамции,
включая сенсоры, вычислители и алгоритмы
КОМПЬЮТЕРНОЕ ЗРЕНИЕ - математические и
алгоритмические аспекты машинного зрения
МАТЕМАТИЧЕСКОЕ ЗРЕНИЕ
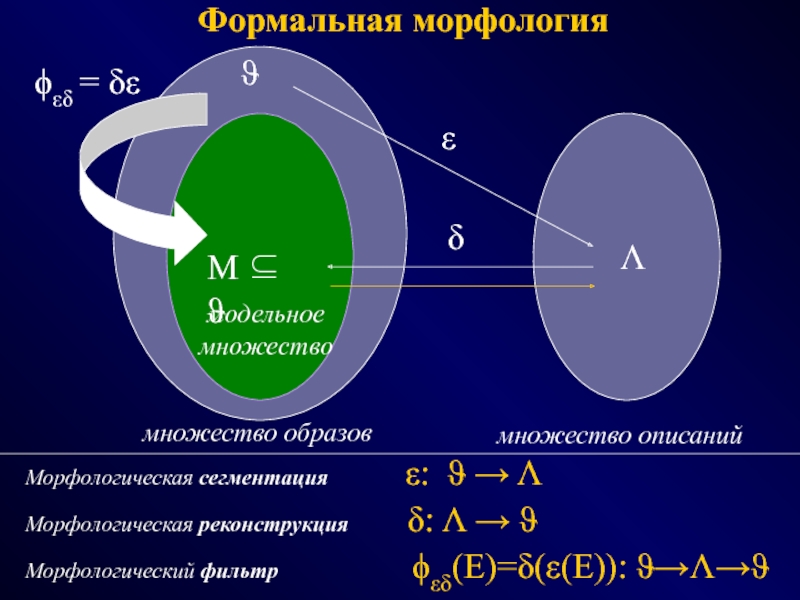
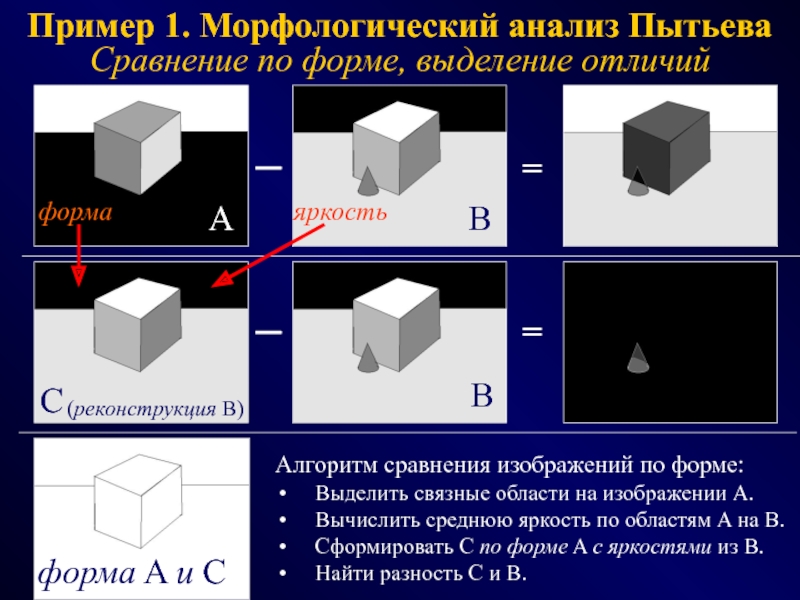
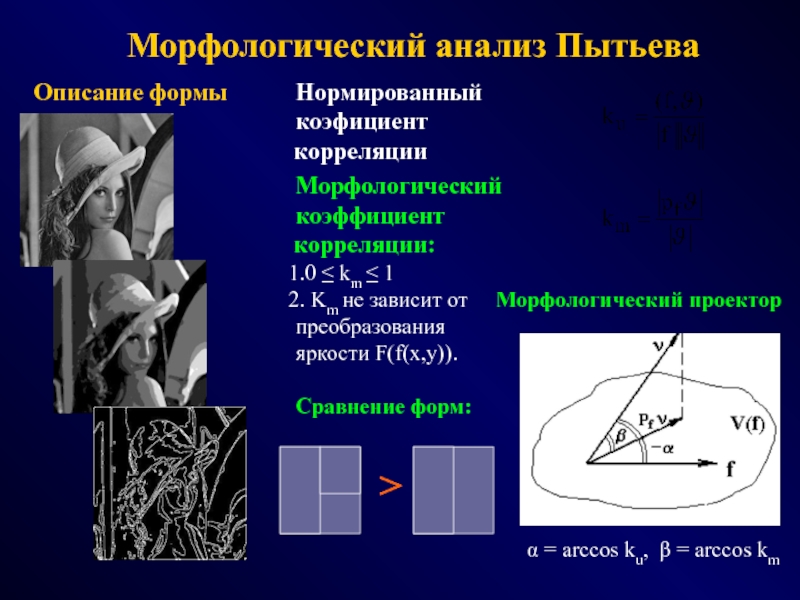
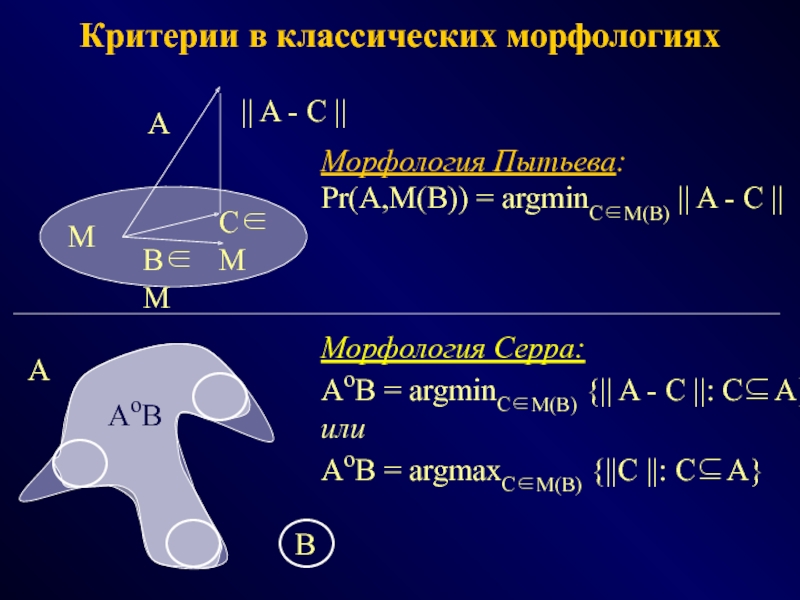
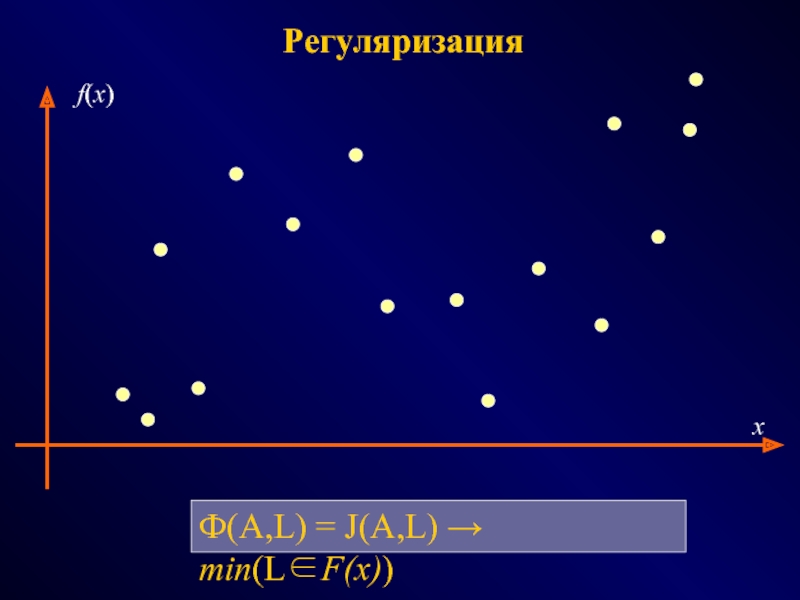
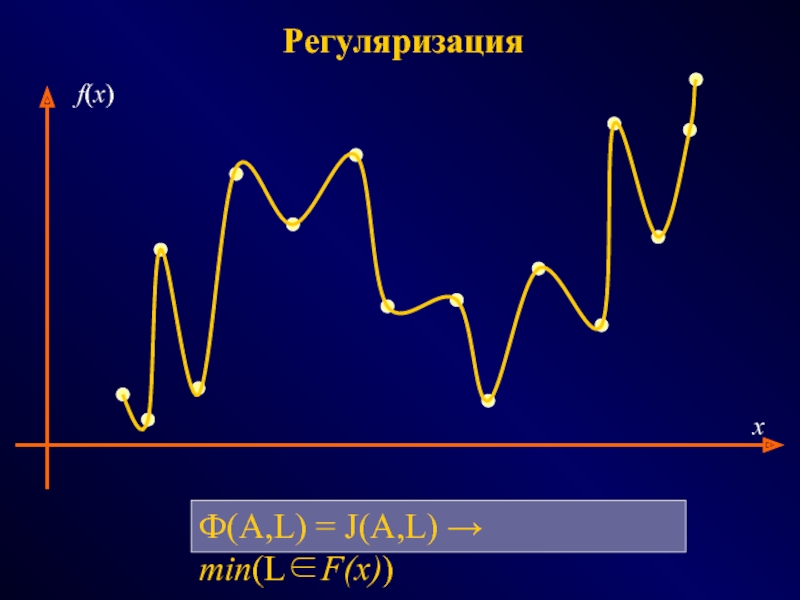
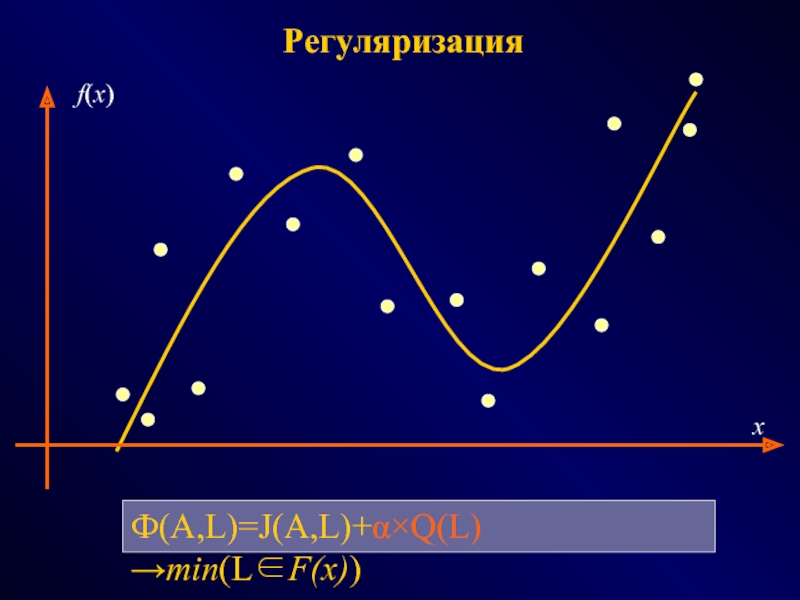
ФОТОГРАММЕТРИЯ МОРФОЛОГИЯ
(геометрия простр.распред. данных) (модели данных и процедур)