Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
НАДЁЖНОСТЬ ПОДВИЖНОГО СОСТАВА
Содержание
- 1. НАДЁЖНОСТЬ ПОДВИЖНОГО СОСТАВА
- 2. 2ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ5.1. ПОНЯТИЕ СИСТЕМЫ
- 3. 35.1. ПОНЯТИЕ СИСТЕМЫЛюбая конструкция состоит из отдельных
- 4. 4Под системой понимают упорядоченное определённым образом множество
- 5. 5ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМЛюбая система имеет:элементный составструктурный
- 6. 6Под элементом системы понимают её составную часть,
- 7. 75.2. ТЕХНОЛОГИЯ ПОСТРОЕНИЯ РАСЧЁТНОЙ СХЕМЫ СИСТЕМЫ (ВАГОНА)При
- 8. 8Для построения расчётной схемы системы нужно определить:Элементный
- 9. 9Все элементы можно разбить на пять групп:ТЕМА
- 10. 10ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ4. Элементы, отказы которых за
- 11. 11При анализе структуры выделяют три случая:ТЕМА 5
- 12. 12Каждый элемент следует отнести к одному из
- 13. 13Если надёжность всех элементов системы обеспечена, то
- 14. 145.3. СТРУКТУРНЫЕ ФУНКЦИИ СИСТЕМРассмотрим способы задания структурных
- 15. 15В зависимости от конкретной структуры системы это
- 16. 16Последовательная структура системыСтруктура, при которой отказ хотя
- 17. 17Параллельная структура системыСтруктура, при которой система работоспособна,
- 18. 18Структура с m исправными из n (или
- 19. 19Пример структуры «2 из 3»ТЕМА 5 НАДЁЖНОСТЬ
- 20. 20Более часто можно встретить смешанное соединение элементов – параллельно-последовательноеТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ(х1*х2)х3(х4*х5)=j(x)=(1–(1 –х1)(1 –х2))х3(1–(1 –х4)(1 –х5))31245
- 21. 215.4. СИСТЕМЫ С ПРИВОДИМОЙ И НЕПРИВОДИМОЙ СТРУКТУРОЙК
- 22. х21х2222На 2 шаге каждый элемент заменяется на
- 23. х5х323Для таких структур просто строить структурные функции.
- 24. 24ЗАМЕЧАНИЕ Для определения надёжности системы с учётом
- 25. 255.5. МЕТОД СТРУКТУРНЫХ СХЕМЗАМЕЧАНИЕ:Далее будем рассматривать только
- 26. 26Элементы могут иметь различные типовые соединения:ТЕМА 5
- 27. 27Надёжность системы с последовательным соединением элементовТЕМА
- 28. 28ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМВБР: рС =ЕСЛИ ОТКАЗЫ ВНЕЗАПНЫЕ
- 29. 29ЕСЛИ все элементы одинаковые: li= const=lТЕМА 5
- 30. 30Надёжность системы с параллельным соединением элементовТЕМА
- 31. 31ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМр1 · р2 ·
- 32. 33ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМС увеличением числа элементов в системе надёжность - увеличиваетсяНапример20,9150,998
- 33. 33ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМРассмотрим надёжность структурной схемы
- 34. 345.6. МЕТОД ПЕРЕБОРА СОСТОЯНИЙТехнология:ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ1.
- 35. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1НАДЁЖНОСТЬ
ПОДВИЖНОГО СОСТАВА
1
Автор:
кандидат технических наук, доцент
кафедры «Вагоны и
вагонное хозяйство»
Александр Анатольевич Иванов
Слайд 33
5.1. ПОНЯТИЕ СИСТЕМЫ
Любая конструкция состоит из отдельных деталей, каждая из
которых должна безотказно работать в течение определённых промежутков времени, величина
которых зависит от заложенного ресурса и периодичности их контрольных проверок (освидетельствований)ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
Предполагая известными показатели надёжности составных частей, рассмотрим подходы к анализу надёжности конструкции в целом.
Для решения этой задачи нужно некоторое идеализированное представление конструкции как системы элементов, находящихся в определённом соотношении,
т.е. нужна РАСЧЁТНАЯ СХЕМА конструкции
Слайд 44
Под системой понимают упорядоченное определённым образом множество элементов,
связанных между
собой и отображающих некоторое целостное единство, т.е. для любой системы
характерно наличие интегративных качеств (свойств) (которые не сводятся к свойствам тех или иных элементов)ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
ОПРЕДЕЛЕНИЕ
Слайд 55
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
Любая система имеет:
элементный состав
структурный состав
Под структурой системы
понимают математическое представление связей:
а) между элементами системы
(типа элемент-элемент)
б) между элементом и
системой
(типа элемент-система)Слайд 66
Под элементом системы понимают её составную часть, которая может характеризоваться
собственными входными и выходными параметрами и рассматриваться как неделимая в
рамках решаемой задачи.ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
Выходной параметр – параметр, который характеризует и обобщает результат использования объекта по назначению
НАПРИМЕР:
надрессорная балка – прочность,
часы – точность
ОПРЕДЕЛЕНИЕ
ОПРЕДЕЛЕНИЕ
Слайд 77
5.2. ТЕХНОЛОГИЯ ПОСТРОЕНИЯ РАСЧЁТНОЙ СХЕМЫ СИСТЕМЫ (ВАГОНА)
При построении расчётной схемы
системы нужно проанализировать её составляющие. Существует много критериев, по которым
элементы включают в расчётную схему. Их выбор зависит от постановки задачи, свойств конструкции, организации эксплуатации и возможностей моделированияТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
Порядок системы – количество элементов, входящих в расчётную схему надёжности системы
ОПРЕДЕЛЕНИЕ
порядок системы ограничен техническими возможностями методов анализа надёжности систем
Чем больше порядок системы, тем ближе расчётная схема к реальной конструкции, однако
Слайд 88
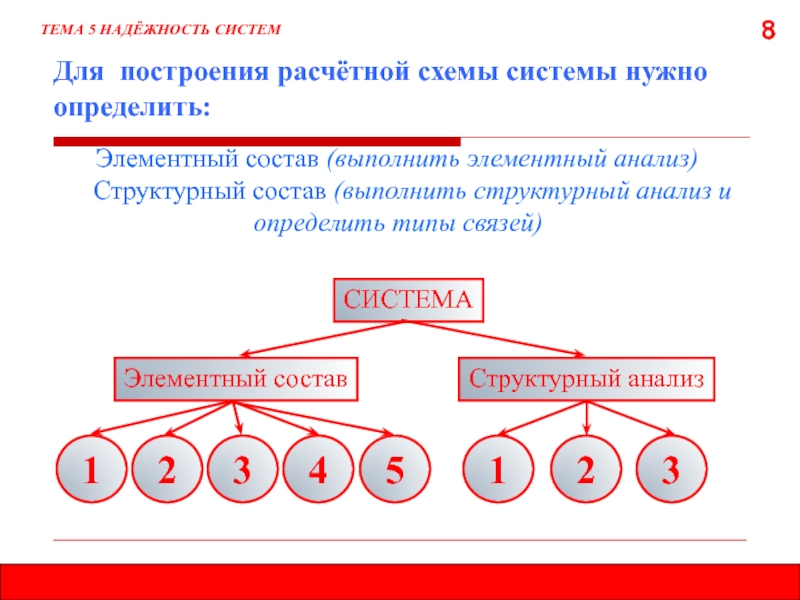
Для построения расчётной схемы системы нужно определить:
Элементный состав (выполнить элементный
анализ)
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
СИСТЕМА
Структурный состав (выполнить структурный анализ и определить
типы связей)Элементный состав
Структурный анализ
1
5
2
3
4
3
2
1
Слайд 99
Все элементы можно разбить на пять групп:
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
1. Элементы,
отказы которых практически не влияют на работоспособность вагона
2. Элементы, работоспособность которых
практически не изменяется за рассматриваемый период времени3. Элементы контролепригодные и ремонтопригодные, контроль технического состояния и ремонт которых возможны не прерывая графика движения поездов (за время стоянки поезда на станции, погрузках и разгрузках)
Слайд 1010
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
4. Элементы, отказы которых за рассматриваемый период времени
могут привести к отказу вагона
5. Элементы, которые: имеют ограниченную контролепригодность при
непосредственном использовании по назначению, могут привести к рушению поезда и для ремонта которых нужны стационарные условия вагонных депоВ расчётную схему «ВАГОН»
нужно включать элементы 5 и 4 групп
Слайд 1111
При анализе структуры выделяют три случая:
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
1. Выходной параметр
элемента не участвует в формировании выходного параметра системы, кроме того
изменение выходного параметра не влияет на состояние других элементов2. Выходной параметр элемента участвует в формировании одного или нескольких
выходных параметров системы
3. Выходной параметр элемента влияет на состояние других элементов. Его изменение эквивалентно изменению внешних условий работы (увеличению нагрузки, температуры и т.п.)
Слайд 1212
Каждый элемент следует отнести к одному из этих случаев.
ТЕМА 5
НАДЁЖНОСТЬ СИСТЕМ
Если в расчётную схему системы входят только элементы, попадающие
только под первый случай, то имеем систему с расчленяемой структурой
(для таких систем надёжность элементов может быть заранее определена вне системы, этот случай характерен для электроники)Если в расчётную схему системы входят элементы второй и третьей групп, то имеем систему со связанной структурой
(для таких систем анализировать надёжность элементов вне системы нужно с большой осторожностью)
Если в расчётную схему входят элементы всех трёх групп, то система имеет комбинированную структуру, которая характерна для вагона
Слайд 1313
Если надёжность всех элементов системы обеспечена, то обычно считают, что
система обязательно работоспособна. Однако это верно только для расчленяемых структур.
ТЕМА
5 НАДЁЖНОСТЬ СИСТЕМБезотказная работа элементов является лишь необходимым, но не достаточным условием безотказной работы системы. Это связано с тем, что допуски на входные параметры элементов системы, как правило, назначаются без учёта всех возможных взаимодействий и взаимовлияний.
Незначительные отклонения свойств отдельных элементов в системах со связанной структурой ощутимо сказываются на выходных параметрах системы в целом. Малые изменения параметров элементов (в пределах допуска) могут тать такое их сочетание, которое скажется на работоспособности всей системы.
Слайд 1414
5.3. СТРУКТУРНЫЕ ФУНКЦИИ СИСТЕМ
Рассмотрим способы задания структурных функций – математических
моделей систем
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
Для обозначения состояния i-го элемента системы
введём булевы переменные:При выводе структурных функций будет учитываться только связи типа «ЭЛЕМЕНТ – СИСТЕМА»
х=(х1, х2, х3, … , хn)
Тогда состояние системы, состоящей из n элементов, можно характеризовать n-мерным вектором:
если i-й элемент в работоспособном состоянии
хi
=
1,
если i-й элемент в неработоспособном состоянии
0,
Множество всех различных состояний системы состоит из 2n штук
Слайд 1515
В зависимости от конкретной структуры системы это множество состояний системы
может быть разбито на два подмножества:
система в работоспособном состоянии
ТЕМА
5 НАДЁЖНОСТЬ СИСТЕММожно задать булеву функцию j(x), которая называется структурной функцией:
система в неработоспособном состоянии
j =j(x), т.е. j =j(х1, х2, х3, … , хn)
Поскольку состояние системы полностью определяется состоянием её элементов, то можем записать:
если система в работоспособном состоянии
j
=
1,
если система в неработоспособном состоянии
0,
Рассмотрим некоторые простейшие структуры систем и соответствующие булевы функции
Слайд 1616
Последовательная структура системы
Структура, при которой отказ хотя бы одного элемента
системы приводит к её отказу
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
Математически это представляется
в виде формулы:min(х1, х2, х3, … , хn)
Которую называют структурной функцией последовательной системы
j(x)
=
П
i=1
n
хi
≡
Архитектура этой структуры:
1
2
3
п
…
Слайд 1717
Параллельная структура системы
Структура, при которой система работоспособна, когда по крайней
мере один элемент в работоспособном состоянии
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
Структурная функция:
mах(х1,
х2, х3, … , хn)j(x)
=
i=1
n
хi
≡
Архитектура этой структуры:
1
1 –
здесь
i=1
n
хi
≡
П
i=1
n
(1– хi)
2
.
n-1
n
=
1– (1– х1)(1– х2)× …×(1– хn)
х1*х2 =1– (1– х1)(1– х2)
Слайд 1818
Структура с m исправными из n (или структура типа «m
из n»)
Структура, при которой система работоспособна, когда по крайней мере
m элементов в работоспособном состоянииТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
Структурная функция:
Структура «п из п» – последовательная
Структура «1 из п» – параллельная
Последовательная и параллельная структуры являются частными случаями систем с «m из n»
если
j(х)
=
1,
если
0,
Слайд 1919
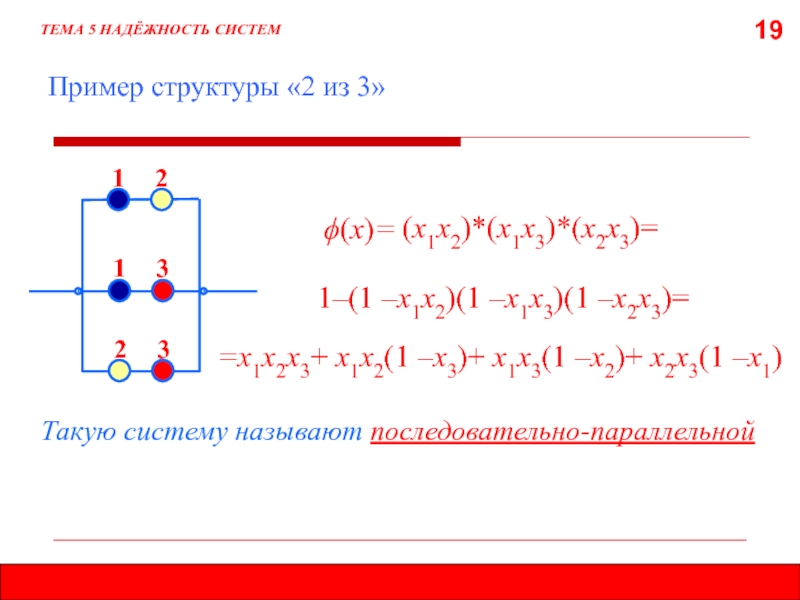
Пример структуры «2 из 3»
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
Такую систему называют
последовательно-параллельной
1
1
2
2
3
3
(х1х2)*(х1х3)*(х2х3)=
j(x)=
1–(1 –х1х2)(1 –х1х3)(1 –х2х3)=
=х1х2х3+ х1х2(1 –х3)+ х1х3(1 –х2)+ х2х3(1 –х1)
Слайд 2020
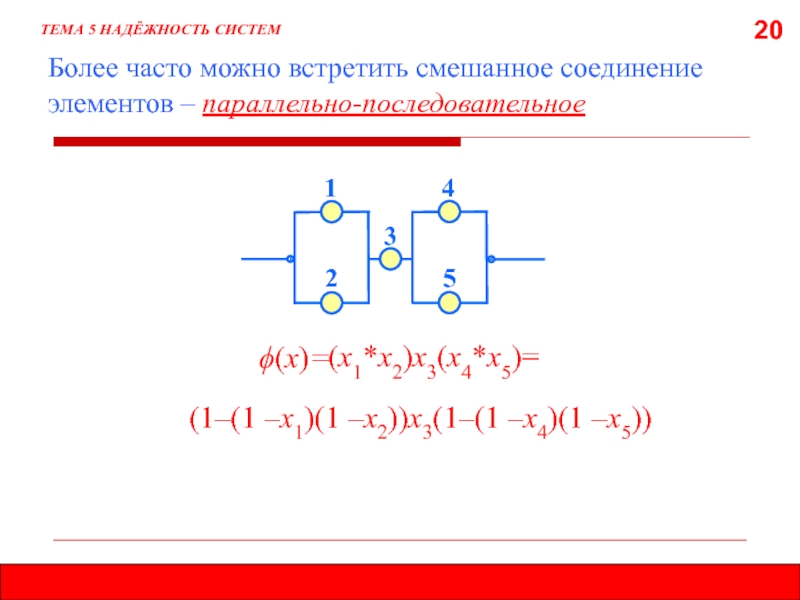
Более часто можно встретить смешанное соединение элементов – параллельно-последовательное
ТЕМА 5
НАДЁЖНОСТЬ СИСТЕМ
(х1*х2)х3(х4*х5)=
j(x)=
(1–(1 –х1)(1 –х2))х3(1–(1 –х4)(1 –х5))
3
1
2
4
5
Слайд 2121
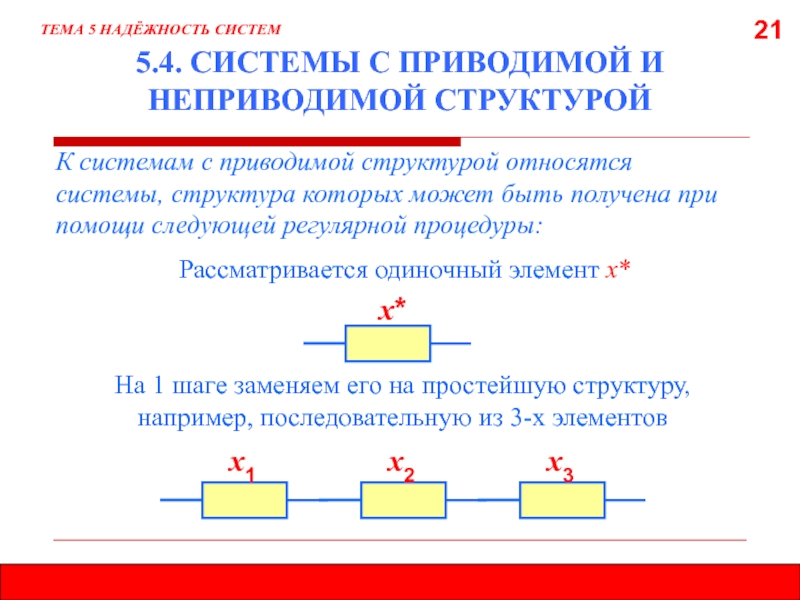
5.4. СИСТЕМЫ С ПРИВОДИМОЙ И НЕПРИВОДИМОЙ СТРУКТУРОЙ
К системам с приводимой
структурой относятся системы, структура которых может быть получена при помощи
следующей регулярной процедуры:ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
Рассматривается одиночный элемент х*
На 1 шаге заменяем его на простейшую структуру, например, последовательную из 3-х элементов
х*
х1
х2
х3
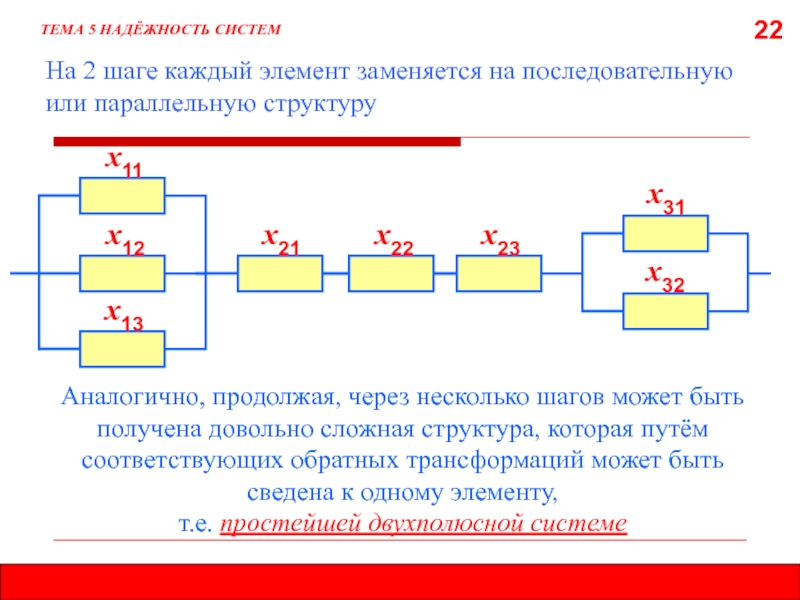
Слайд 22х21
х22
22
На 2 шаге каждый элемент заменяется на последовательную или параллельную
структуру
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
Аналогично, продолжая, через несколько шагов может быть
получена довольно сложная структура, которая путём соответствующих обратных трансформаций может быть сведена к одному элементу,
т.е. простейшей двухполюсной системех11
х31
х32
х12
х13
х23
Слайд 23х5
х3
23
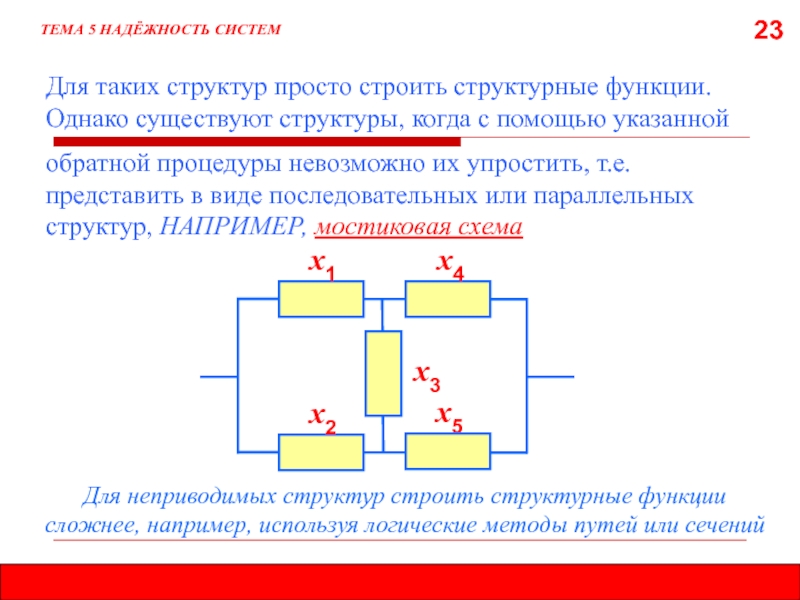
Для таких структур просто строить структурные функции.
Однако существуют структуры, когда
с помощью указанной
обратной процедуры невозможно их упростить, т.е. представить
в виде последовательных или параллельных структур, НАПРИМЕР, мостиковая схемаТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
Для неприводимых структур строить структурные функции сложнее, например, используя логические методы путей или сечений
х1
х4
х2
Слайд 2424
ЗАМЕЧАНИЕ
Для определения надёжности системы с учётом её структуры используют:
метод структурных
схем;
метод перебора состояний;
метод логических схем с применением алгебры логики (например,
метод путей или метод сечений);метод дерева событий или дерева отказов; графовый метод.
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
Слайд 2525
5.5. МЕТОД СТРУКТУРНЫХ СХЕМ
ЗАМЕЧАНИЕ:
Далее будем рассматривать только расчленяемые системы
ТЕМА 5
НАДЁЖНОСТЬ СИСТЕМ
Реальная система отображается в виде структурной схемы работы её
элементовКаждый элемент, включённый в расчётную схему надёжности представляется в виде блока
ДОПУЩЕНИЯ:
- элементы имеют независимые отказы
- связи элементов абсолютно надёжны, их отказы невозможны
- элементы имеют только два состояния:
0 – неработоспособное,
1 – работоспособное)
Слайд 2626
Элементы могут иметь различные типовые соединения:
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
- последовательное
-
параллельное
- с m исправными из n
- мостиковое
- с ненагруженным резервом
-
комбинированноеСлайд 2727
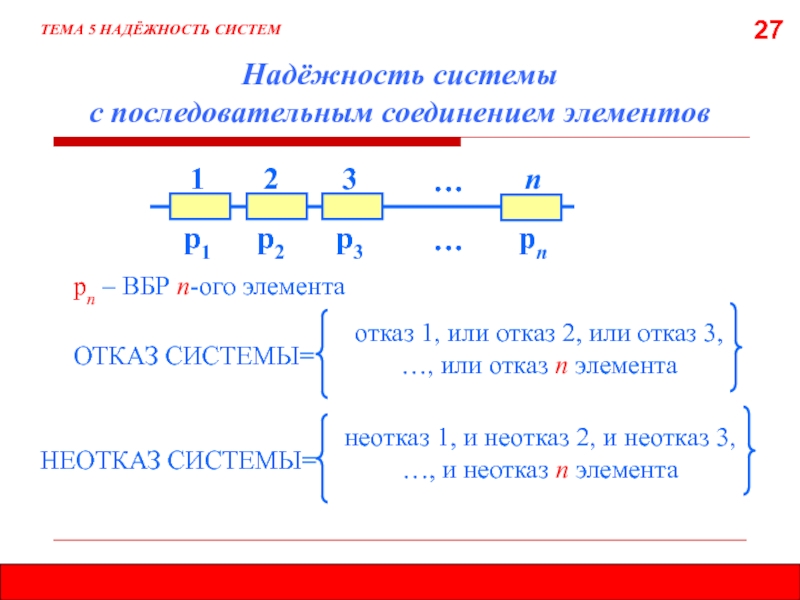
Надёжность системы
с последовательным соединением элементов
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
рп –
ВБР п-ого элемента
ОТКАЗ СИСТЕМЫ=
р1
р2
р3
рп
…
1
2
3
п
…
отказ 1, или отказ 2,
или отказ 3, …, или отказ п элементаНЕОТКАЗ СИСТЕМЫ=
неотказ 1, и неотказ 2, и неотказ 3, …, и неотказ п элемента
Слайд 2828
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
ВБР: рС =
ЕСЛИ ОТКАЗЫ ВНЕЗАПНЫЕ
e–lit
р1 ·
р2 ·
р3 × …
× рп =
П
i=1
n
рi
FС =
1 –
рC
=1 –
П
i=1
n
рi
=1– e–lit
р
при этом, среднее время безотказной работы:
EXP(–lit )=
П
i=1
n
Мx=
C
(t)=
EXP(–Slit )=
i=1
n
EXP(–lSt )
Т
=
1
lS
lS – суммарная интенсивность отказов элементов системы
pi(t)=
Fi(t)
Слайд 2929
ЕСЛИ все элементы одинаковые: li= const=l
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
С увеличением
числа элементов в системе
надёжность - снижается
Например
р
е
– nlt
C
(t)=
i
(t)
=р
10
0,912
100
0,398
n
Слайд 3030
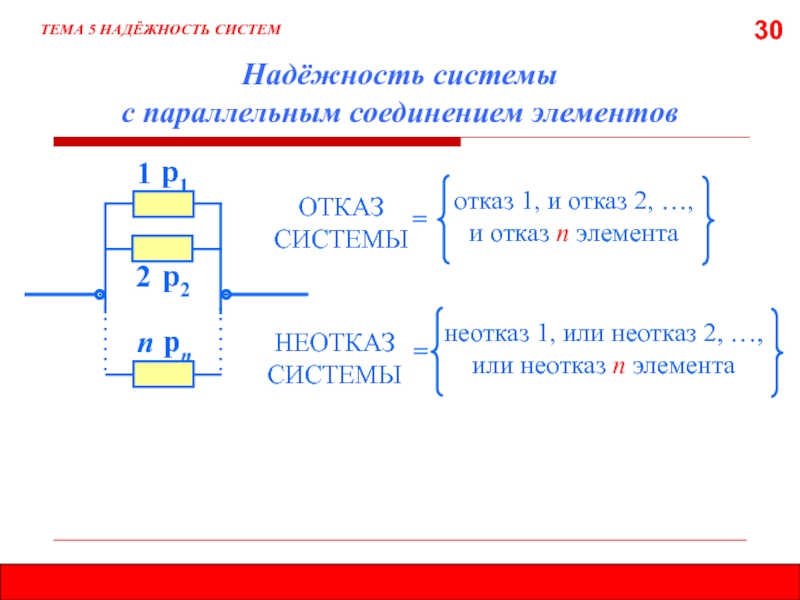
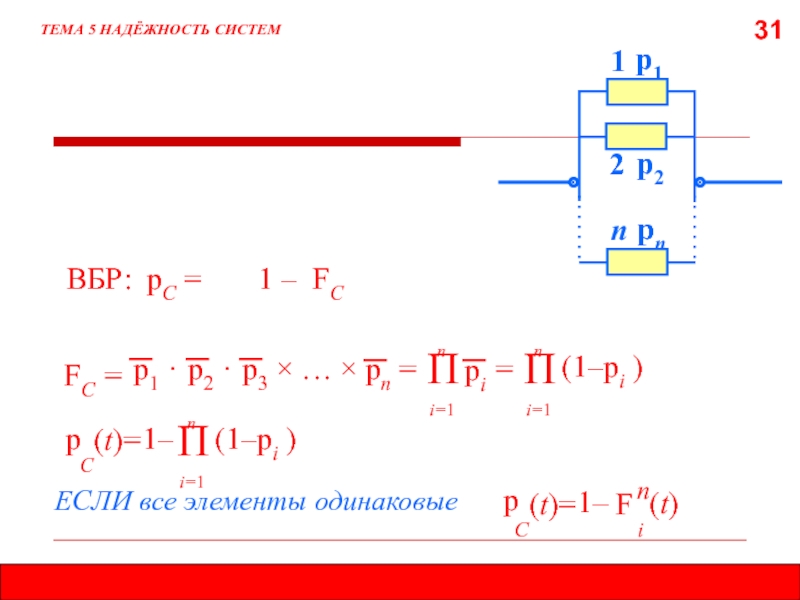
Надёжность системы
с параллельным соединением элементов
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
р1
р2
рп
1
2
п
отказ 1,
и отказ 2, …,
и отказ п элемента
ОТКАЗ СИСТЕМЫ
=
неотказ 1,
или неотказ 2, …,
или неотказ п элементаНЕОТКАЗ СИСТЕМЫ
=
Слайд 3131
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
р1 ·
р2 ·
р3 × …
× рп =
П
i=1
n
рi
ВБР: рС =
1 –
FC
р
C
(t)=
FС
=
П
i=1
n
рi
=
(1–
)
1–
П
i=1
n
рi
(1–
)
ЕСЛИ все
элементы одинаковыер
1–
C
(t)=
i
(t)
F
n
Слайд 3233
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
С увеличением числа элементов в системе
надёжность
- увеличивается
Например
2
0,91
5
0,998
Слайд 3333
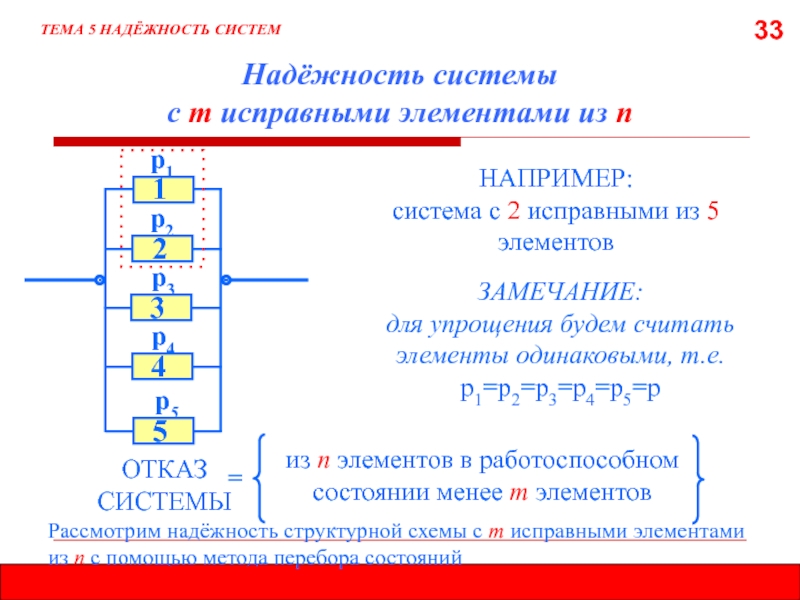
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
Рассмотрим надёжность структурной схемы с m исправными
элементами из n с помощью метода перебора состояний
р1
р3
р5
из n элементов
в работоспособном состоянии менее т элементовОТКАЗ СИСТЕМЫ
=
р2
2
5
р4
4
1
3
НАПРИМЕР:
система с 2 исправными из 5 элементов
ЗАМЕЧАНИЕ:
для упрощения будем считать элементы одинаковыми, т.е. р1=р2=р3=р4=р5=р
Надёжность системы
с т исправными элементами из п
Слайд 3434
5.6. МЕТОД ПЕРЕБОРА СОСТОЯНИЙ
Технология:
ТЕМА 5 НАДЁЖНОСТЬ СИСТЕМ
1. Составить таблицу состояний
элементов системы
2. Определить для каждого случая состояние системы (работоспособное или неработоспособное)
3. Определить
вероятность каждого состояния системы4. Определить вероятность безотказной работы системы