Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Некоторые элементы МС
Содержание
- 1. Некоторые элементы МС
- 2. Основная задача МСОценка и анализ параметров распределения
- 3. Основные цели МСПрогнозирование поведения СВПроверка соответствия значений, полученных оценок некоторым регламентированным характеристикам
- 4. Генеральная совокупностьГенеральной совокупностью называется вероятностное пространство с
- 5. Статистическая оценкаСтатистической оценкой некоторого параметра
- 6. Выборочное значениеКонкретное значение статистической оценки на данной конкретной выборке называют выборочным значением или выборочной оценкой
- 7. Распределение выборкиОписание и систематизацию выборки удобно проводить
- 8. Вариационный рядБудем предполагать при этом, что выборка
- 9. Статистический рядНаряду с вариационным рядом рассматривается статистический
- 10. Эмпирическая функция распределения (ФР)Эмпирическая ФР есть функция,
- 11. Мода СВМодой непрерывной СВ называют
- 12. Пример: Пусть дсв распределена по закону: тогда её
- 13. Выборочная совокупностьВыборочной совокупностью (выборкой) называется совокупность случайно
- 14. Выборки и их характеристикиОбъёмом выборки называется число
- 15. Относительные частоты Пусть имеется выборка объёма «n» где
- 16. О таблице:В таблице: -
- 17. Ещё о таблице:Таблица, устанавливающая соответствие между значениями
- 18. Ещё о таблице:Если СВ является непрерывной СВ,
- 19. Ещё о таблице:Если СВ
- 20. Полигон распределенияПри большом объёме выборки не имеет
- 21. ГистограммыДля иллюстрации распределения н.с.в. Пользуются диаграммами, называемые
- 22. ПримерВ результате испытания СВ приняла следующие значения: Требуется: 1) составить таблицу распределения 2) изобразить полигон частот
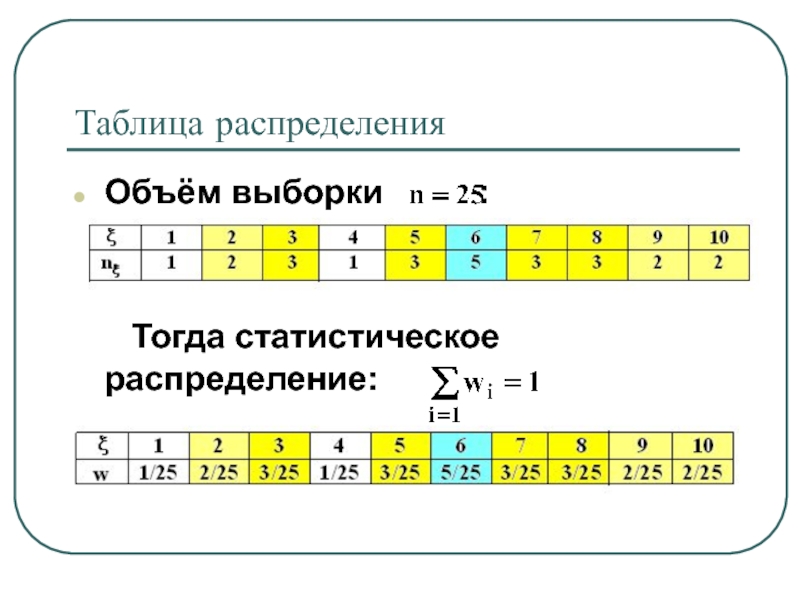
- 23. Таблица распределенияОбъём выборки : Тогда статистическое распределение:
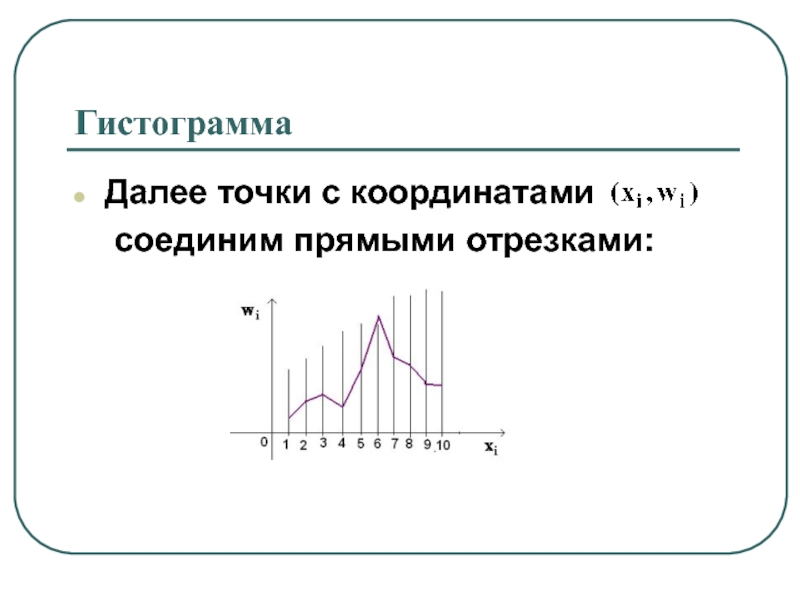
- 24. ГистограммаДалее точки с координатами соединим прямыми отрезками:
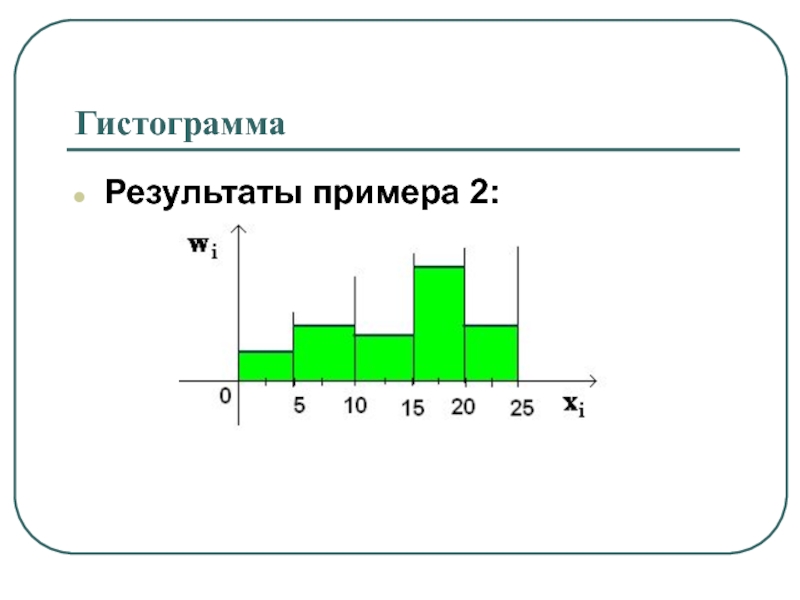
- 25. Пример2:В результате испытания СВ приняла значения: Требуется:
- 26. ГистограммаРезультаты примера 2:
- 27. Статистическая функция распределенияПусть
- 28. Скачать презентанцию
Основная задача МСОценка и анализ параметров распределения изучаемой случайной величины (СВ) или самого вида (типа) распределения по данным выборки её значений
Слайды и текст этой презентации
Слайд 3Основные цели МС
Прогнозирование поведения СВ
Проверка соответствия значений, полученных оценок некоторым
регламентированным характеристикам
Слайд 4Генеральная совокупность
Генеральной совокупностью называется вероятностное пространство с определённой на нём
СВ
Совокупность значений
СВ из генеральной совокупности называется случайной выборкой объёма,
равного n Слайд 5Статистическая оценка
Статистической оценкой некоторого параметра распределения СВ называется
функция, определённая на множестве выборок значений СВ:
,
значения которой
близки к теоретическому значению Слайд 6Выборочное значение
Конкретное значение статистической оценки на данной конкретной выборке называют
выборочным значением или выборочной оценкой
Слайд 7Распределение выборки
Описание и систематизацию выборки удобно проводить с помощью понятия
распределения выборки: распределением выборки
называется распределение вероятностей вспомогательной СВ
принимающей значенияс одинаковой вероятностью
Слайд 8Вариационный ряд
Будем предполагать при этом, что выборка
является вариационным рядом
из элементов выборки, расположенных в неубывающем порядке:Разность называется размахом выборки
Слайд 9Статистический ряд
Наряду с вариационным рядом рассматривается статистический ряд:
где
называются частотами,
число элементов выборки, значения которых
равны значениям . При этом Слайд 10Эмпирическая функция распределения (ФР)
Эмпирическая ФР есть функция, определяемая формулой:
- число элементов выборки, не превосходящих
«x»Слайд 11Мода СВ
Модой непрерывной СВ называют то её возможное
значение, которому соответствует локальный максимум плотности распределения СВ.
Модой дискретной
СВ называется её наиболее вероятное значение.Слайд 12Пример:
Пусть дсв распределена по закону:
тогда её модой является число:
Пусть дана нсв, для которой плотность задана:
Тогда, находя локальный максимум
её получим: Слайд 13Выборочная совокупность
Выборочной совокупностью (выборкой) называется совокупность случайно отобранных однородных объектов.
Генеральной
совокупностью называется совокупность всех однородных объектов, из которых производится выборка.
Слайд 14Выборки и их характеристики
Объёмом выборки называется число объектов этой совокупности.
Выборка
называется репрезентативной (представительной), если достаточно хорошо представляет количественные соотношения генеральной
совокупности.Слайд 15Относительные частоты
Пусть имеется выборка объёма «n»
где - значения
СВ соответственно в -
ом испытании. Среди проверенных значений могут быть и равные. Объединив равные значения СВ получим таблицу:Слайд 16О таблице:
В таблице: - число появлений значений
, называемое частотами соответствующих значений
случайной величины- объем выборки. Отношения называются относительными частотами.
Слайд 17Ещё о таблице:
Таблица, устанавливающая соответствие между значениями СВ и их
относительными частотами называется статистическим распределением СВ:
Слайд 18Ещё о таблице:
Если СВ является непрерывной СВ, то её статистическое
распределение представляется в виде:
здесь - относительные частоты попадания
СВ в соответствующий интервал Слайд 19Ещё о таблице:
Если СВ принимает
значений, равных , то в случае чётного
числаполовину значений можно относить к к соседним интервалам: т.е. половину значений к интервалу , а вторую половину к интервалу . При нечётном значении : к одному из интервалов отнести значений, к другому
значений.