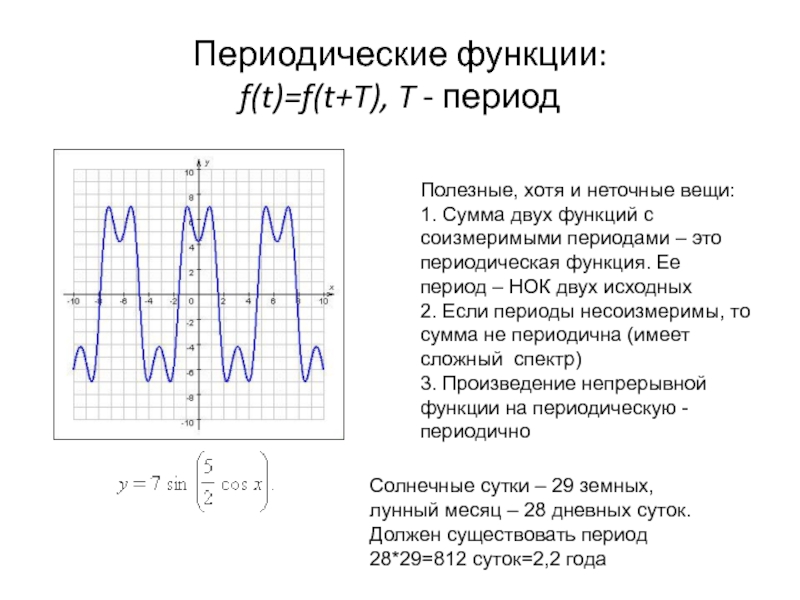
Слайд 2Полезные, хотя и неточные вещи:
1. Сумма двух функций с соизмеримыми
периодами – это периодическая функция. Ее период – НОК двух
исходных
2. Если периоды несоизмеримы, то сумма не периодична (имеет сложный спектр)
3. Произведение непрерывной функции на периодическую - периодично
Периодические функции:
f(t)=f(t+T), T - период
Солнечные сутки – 29 земных, лунный месяц – 28 дневных суток.
Должен существовать период 28*29=812 суток=2,2 года
Слайд 3Частным случаем таких функций являются гармонические функции
где A – амплитуда
гармоники, ωt+ϕ - ее фаза. Фаза гармоники не меняется, если
к ней алгебраически прибавить 2π – период гармоник.
Важнейшими для использования в задачах динамической метеорологии свойствами гармоник являются:
Теоремы сложения аргументов, например, теорема косинусов
Формулы преобразования суммы в произведение и произведения в суммы, например,
Слайд 4Амплитудно-фазовое представление гармоник
Слайд 5
Комплексное представление гармоник
Слайд 6Зачем нужно ?
Комплексное представление удобно, если нужно преобразовывать функцию
Дело в
том, что экспонента переходит сама в себя при дифференцировании или
интегрировании
Это важно для теоретического анализа
Слайд 7а — одиночная волна; б — цуг волн; в —
бесконечная синусоидальная волна.
Только бесконечная периодическая функция разлагается в ряд Фурье.
Пакеты и импульсы конечной длины представимы только интегралом Фурье.
Волны в природе и теории
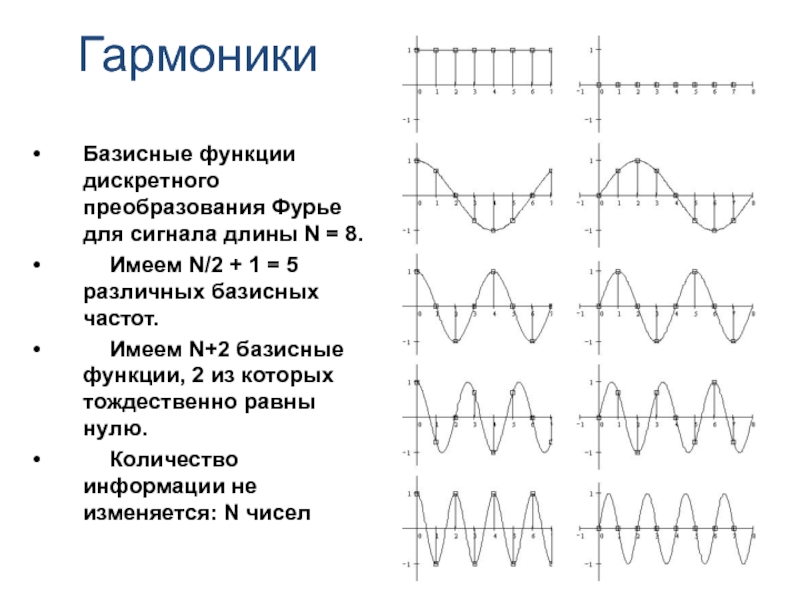
Слайд 8Гармоники
Базисные функции дискретного преобразования Фурье для сигнала длины N =
8.
Имеем N/2 + 1 = 5 различных базисных частот.
Имеем N+2
базисные функции, 2 из которых тождественно равны нулю.
Количество информации не изменяется: N чисел
Слайд 9Гармонический анализ = разложение в ряд Фурье
Все метеорологические поля периодичны
по долготе и по широте вследствие близкой к сфере формы
земной поверхности. Если функция имеет период L, то ее можно представить в виде бесконечного ряда Фурье по синусам и косинусам в виде
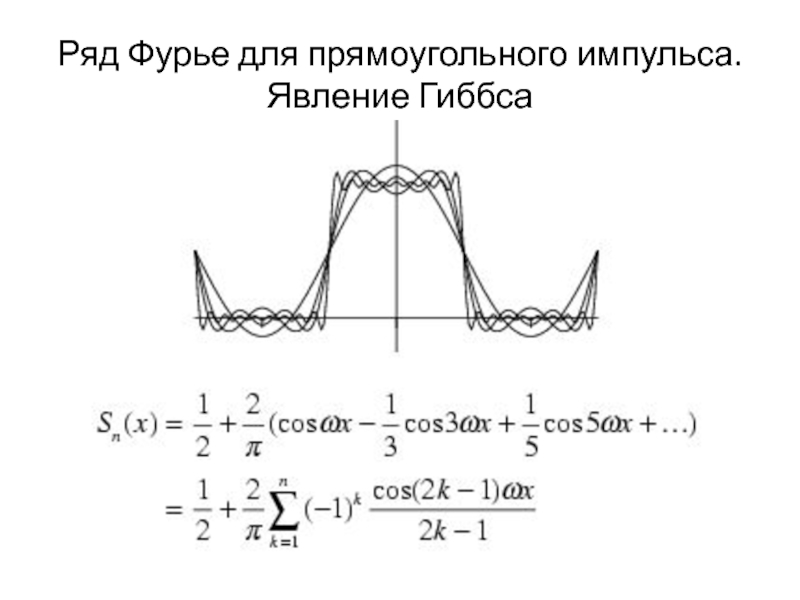
Слайд 10Ряд Фурье для прямоугольного импульса. Явление Гиббса
Слайд 11Используя экспоненциальное представление гармоник, ряд Фурье можно записать в виде:
Слайд 12Если функция не периодична, то она представима интегралом Фурье
Замена функции
на ее интеграл Фурье называется преобразованием Фурье.
Оно представляет функцию
не в физическом пространстве, а в «пространстве волновых чисел» или «пространстве частот колебаний»
Слайд 13Колебания – это периодические изменения параметра (параметров) во времени.
Виды колебаний:
собственные
свободные
затухающие
вынужденные
вызываемые периодическим воздействием
автоколебания, вызываемые непериодическим воздействием
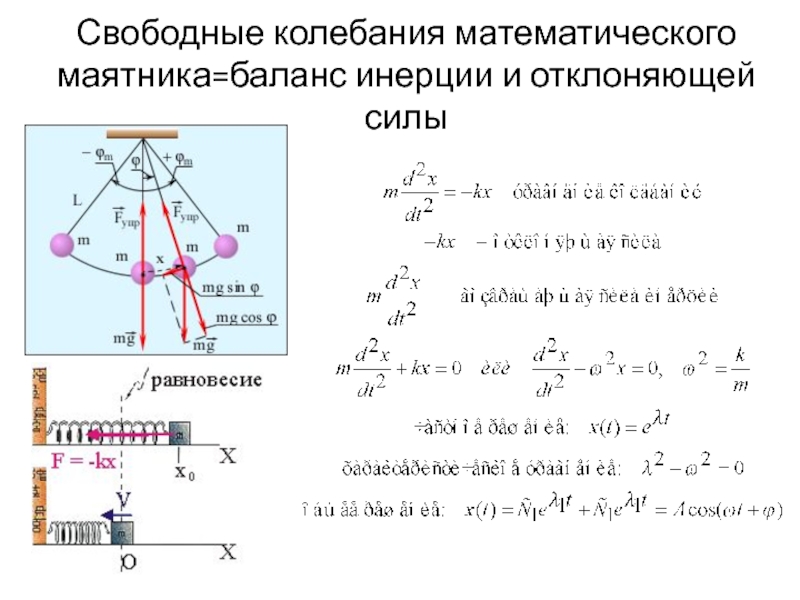
Слайд 14Свободные колебания математического маятника=баланс инерции и отклоняющей силы
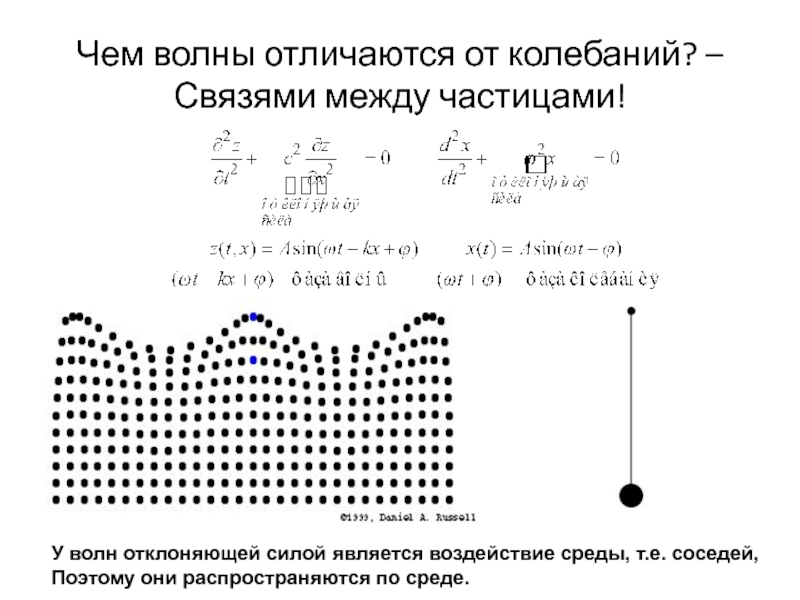
Слайд 15Чем волны отличаются от колебаний? – Связями между частицами!
У волн
отклоняющей силой является воздействие среды, т.е. соседей,
Поэтому они распространяются по
среде.
Слайд 16Виды волн – по направление движения частиц: продольные поперечные, вертикальные
Слайд 17Сравнение математического
Описания колебания и волны
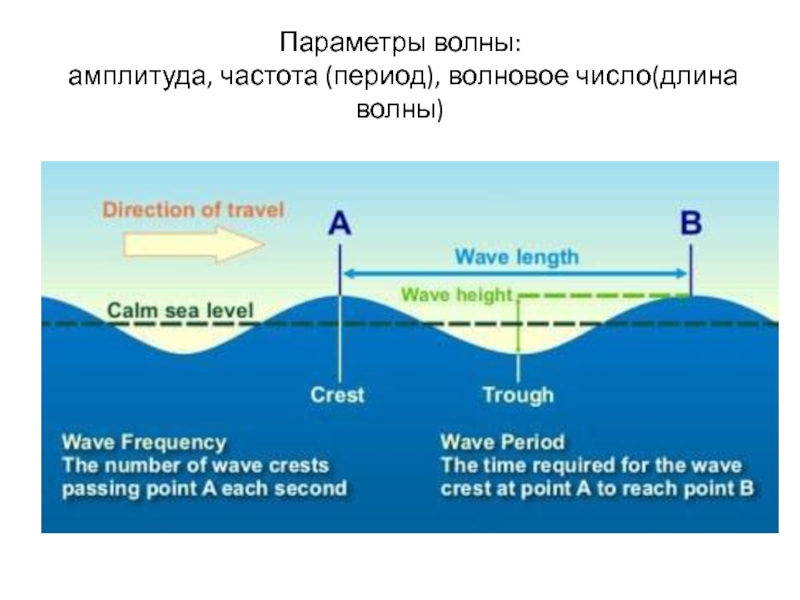
Слайд 18Параметры волны:
амплитуда, частота (период), волновое число(длина волны)
Слайд 19 Фазовая скорость одномерной волны
Слайд 20Дисперсия и групповая скорость волн
(одномерный случай)
При сложении колебаний с близкими
частотами возникают биения.
Фазовая скорость распространения огибающей волнового пакета называется
групповой скоростью
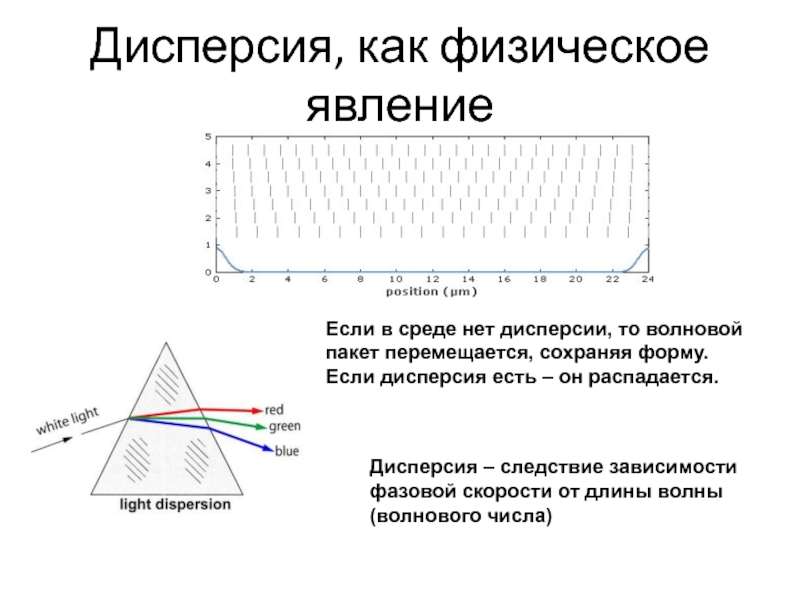
Слайд 21Дисперсия, как физическое явление
Дисперсия – следствие зависимости фазовой скорости от
длины волны (волнового числа)
Если в среде нет дисперсии, то волновой
пакет перемещается, сохраняя форму.
Если дисперсия есть – он распадается.
Слайд 23Линейные волны
Волновой вектор k=k1i+k2j
Слайд 25Линейные волновые явления
(отражение, преломление, диффракция, интерференция, резонанс, эффект Допплера)
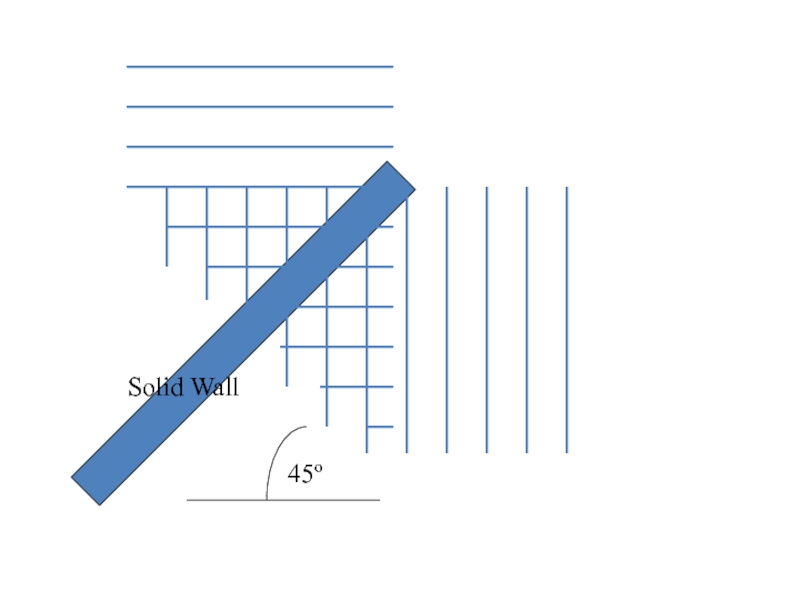
Слайд 26WHEN WAVES HIT A SOLID SURFACE THEY REFLECT
THE ANGLE OF
REFLECTION IS THE SAME AS THE ANGLE OF INCIDENCE
r =
i
REFLECTION
REFLECTION
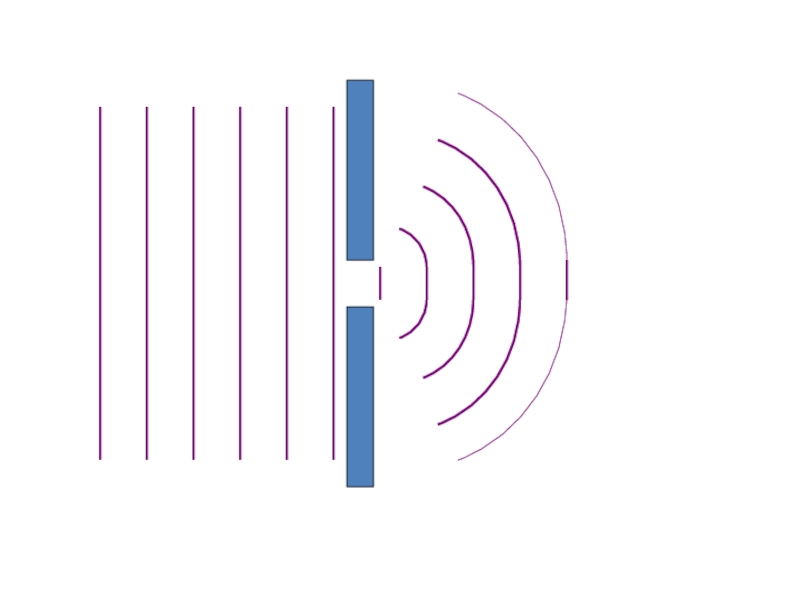
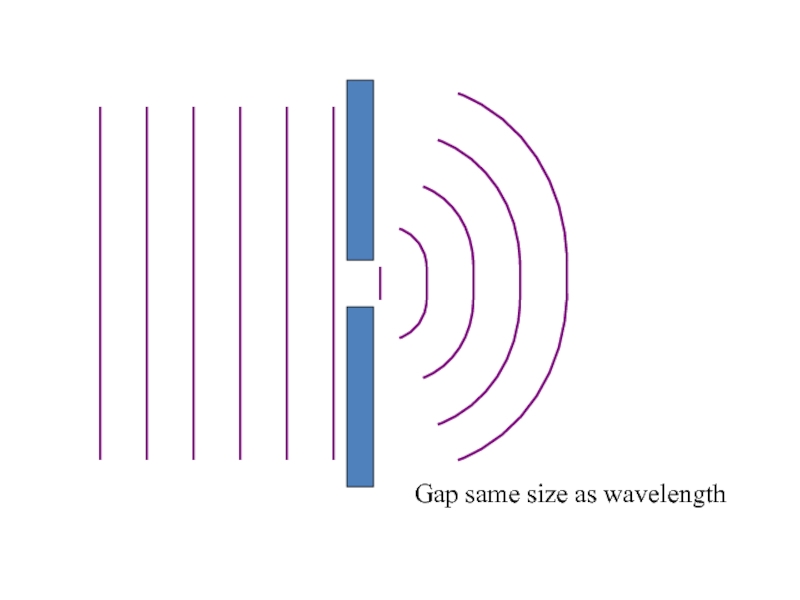
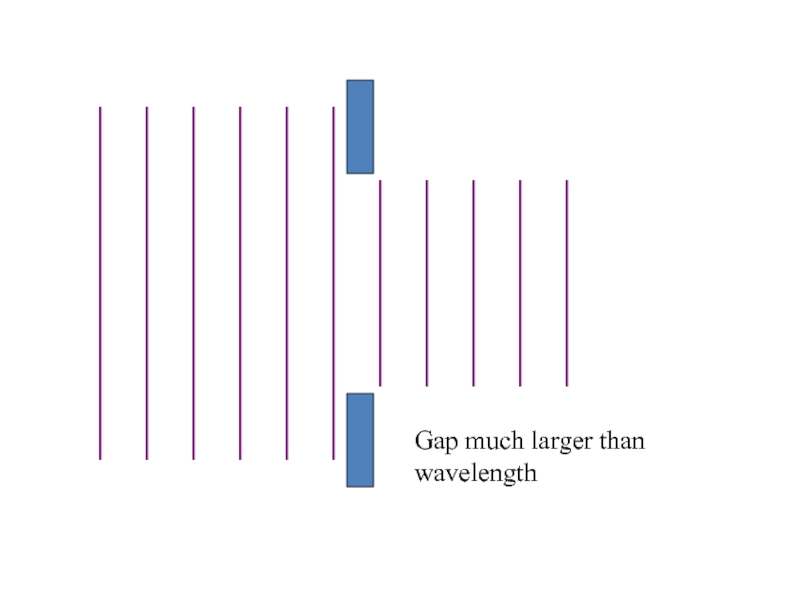
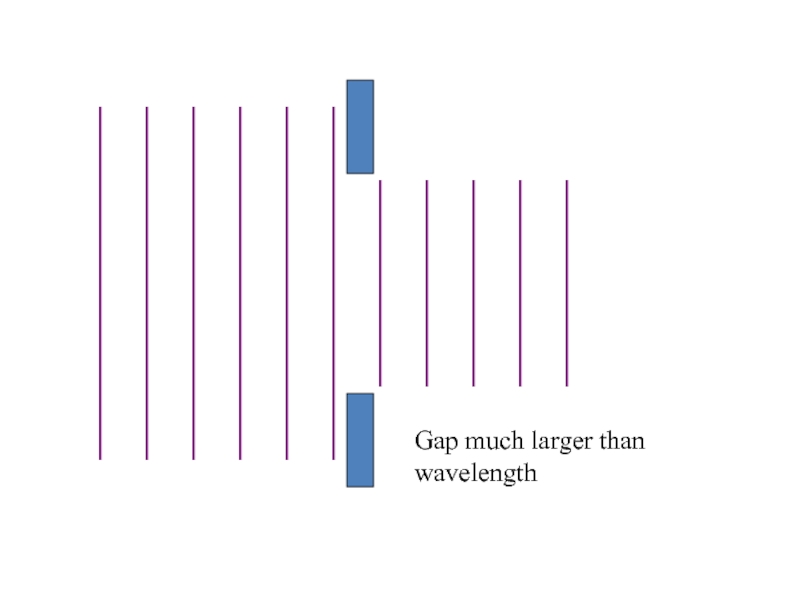
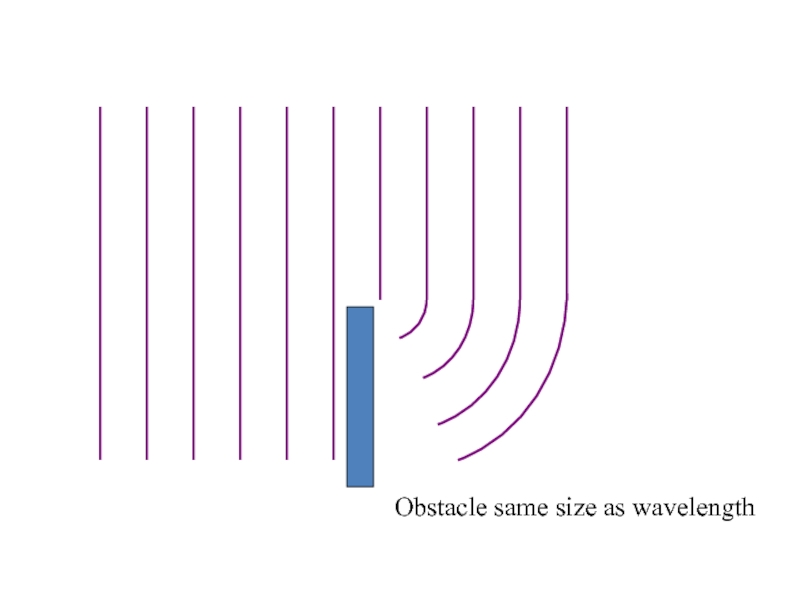
Слайд 29Diffraction
When waves pass through a gap they can bend round
the edges of the gap
The effect is most noticeable when
the gap size is similar to the wavelength
Слайд 34
Obstacle same size as wavelength
Слайд 35
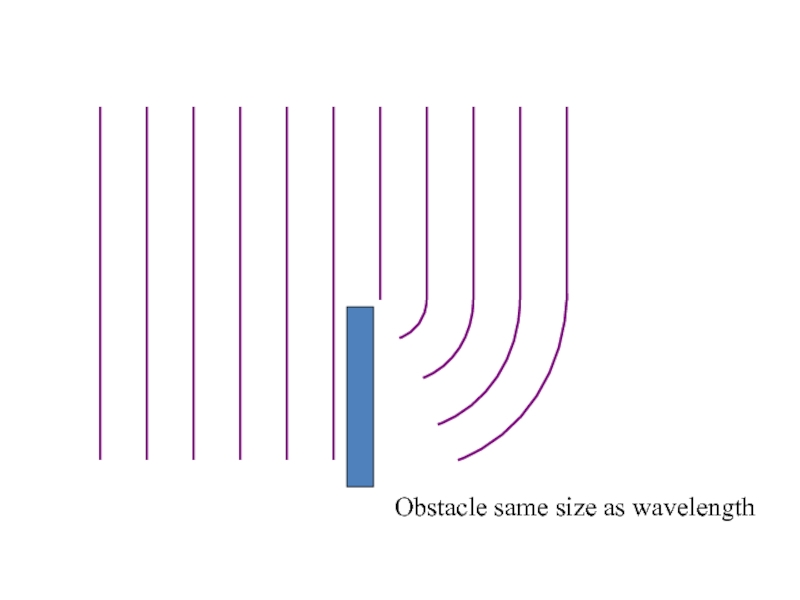
Obstacle same size as wavelength
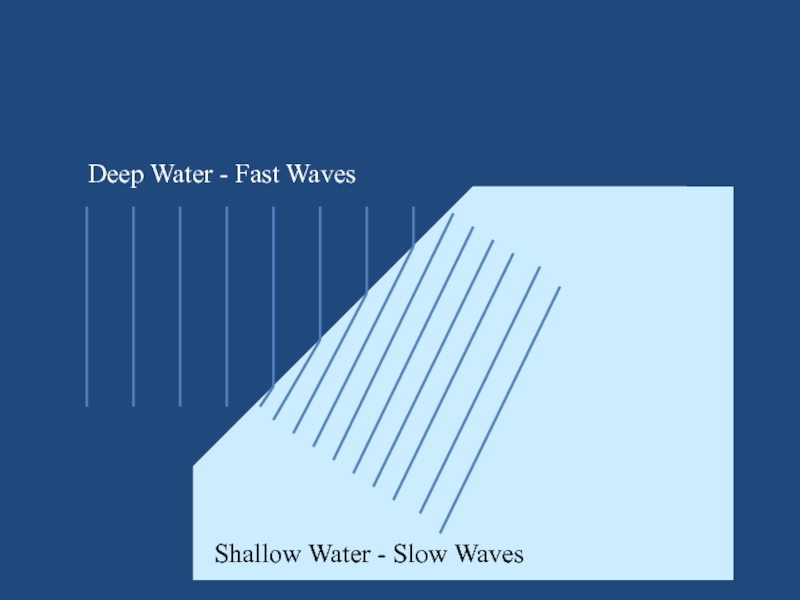
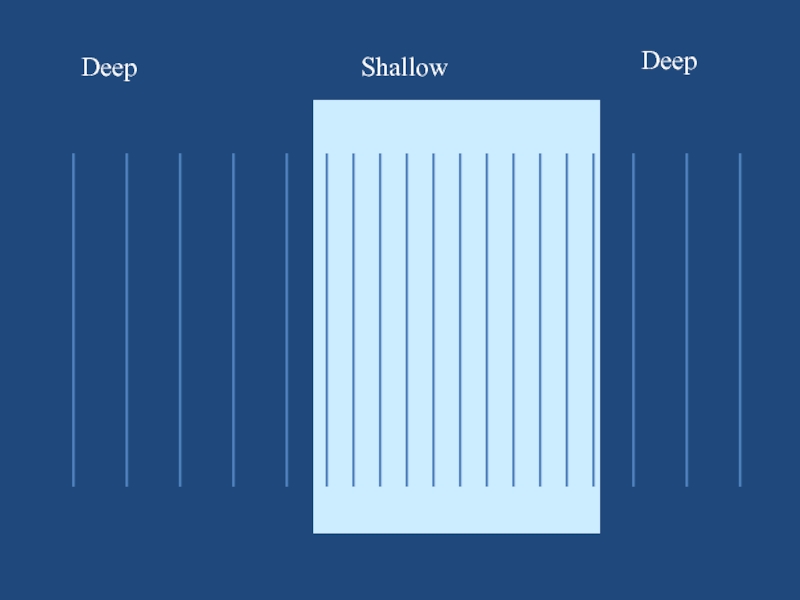
Слайд 36Refraction
When wavefronts slow down they may change direction.
Water waves slow
down in shallow water
Слайд 37Deep Water - Fast Waves
Shallow Water - Slow Waves
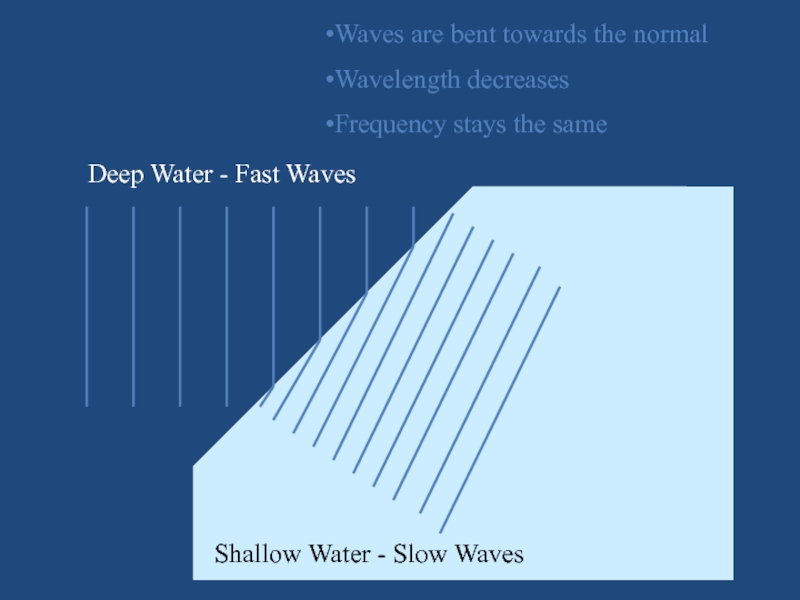
Слайд 38Deep Water - Fast Waves
Shallow Water - Slow Waves
Waves are
bent towards the normal
Wavelength decreases
Frequency stays the same
Слайд 40
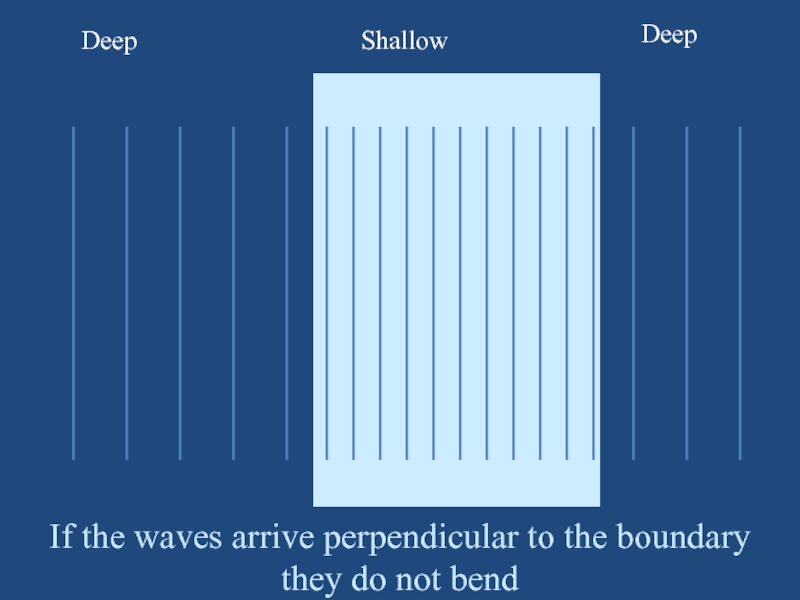
Deep
Deep
Shallow
If the waves arrive perpendicular to the boundary they do
not bend
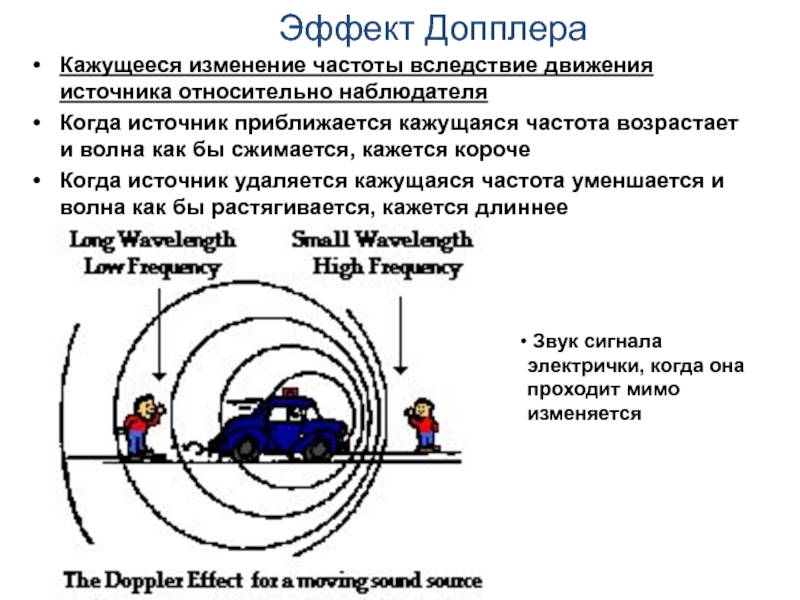
Слайд 42Эффект Допплера
Кажущееся изменение частоты вследствие движения источника относительно наблюдателя
Когда источник
приближается кажущаяся частота возрастает и волна как бы сжимается, кажется
короче
Когда источник удаляется кажущаяся частота уменшается и волна как бы растягивается, кажется длиннее
Звук сигнала электрички, когда она проходит мимо изменяется
Слайд 43Резонанс
7 ноября 1940 г. Новый и широко разрекламированный подвесной мост
на р. Такома (США)
Развалился под действием ветра в результате возникновения
резонанса
Слайд 44Нелинейные волновые явления
Самофокусировка.
Солитоны
Слайд 45Нелинейность волн – зависимость скорости распространения волны от ее амплитуды
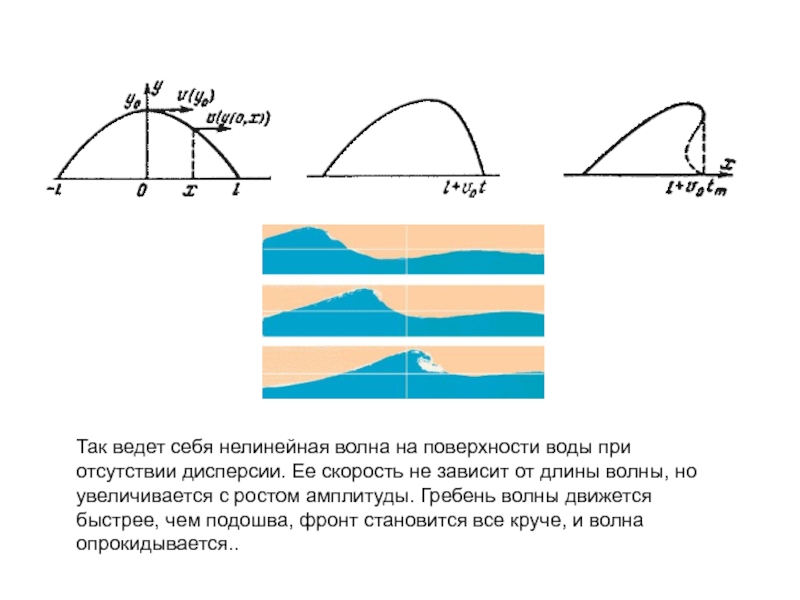
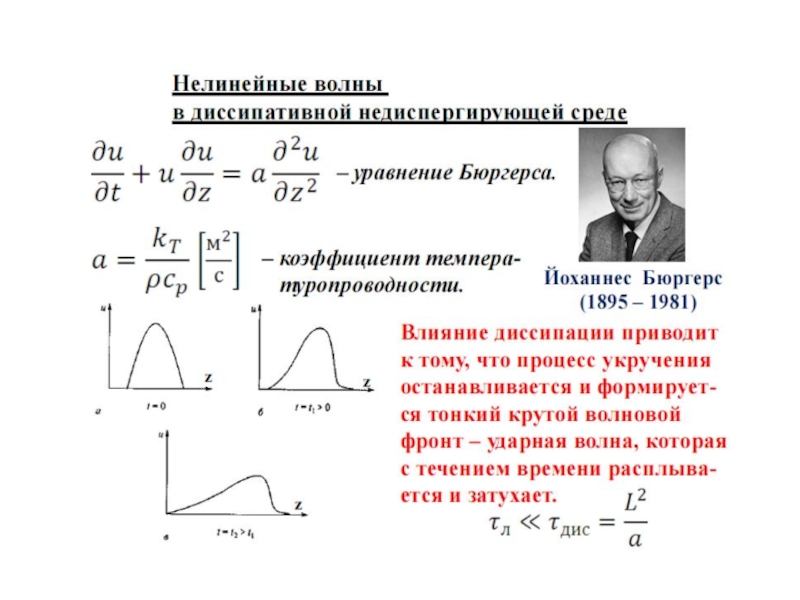
Слайд 47Так ведет себя нелинейная волна на поверхности воды при отсутствии
дисперсии. Ее скорость не зависит от длины волны, но увеличивается
с ростом амплитуды. Гребень волны движется быстрее, чем подошва, фронт становится все круче, и волна опрокидывается..
Слайд 50Солитон Джона Рассела. 1834
"Я следил за движением баржи, которую быстро
тянула по узкому каналу пара лошадей, когда баржа неожиданно остановилась.
Но масса воды, которую баржа привела в движение, собралась около носа судна в состоянии бешеного движения, затем неожиданно оставила его позади, катясь вперед с огромной скоростью и принимая форму большого одиночного возвышения - округлого, гладкого и четко выраженного водяного холма. Он продолжал свой путь вдоль канала, нисколько не меняя своей формы и не снижая скорости. Я последовал за ним верхом, и когда нагнал его, он по-прежнему катился вперед со скоростью примерно 8-9 миль в час, сохранив свой первоначальный профиль возвышения длиной около тридцати футов и высотой от фута до полутора футов. Его высота постепенно уменьшалась, и после одной или двух миль погони я потерял его в изгибах канала".
Слайд 53
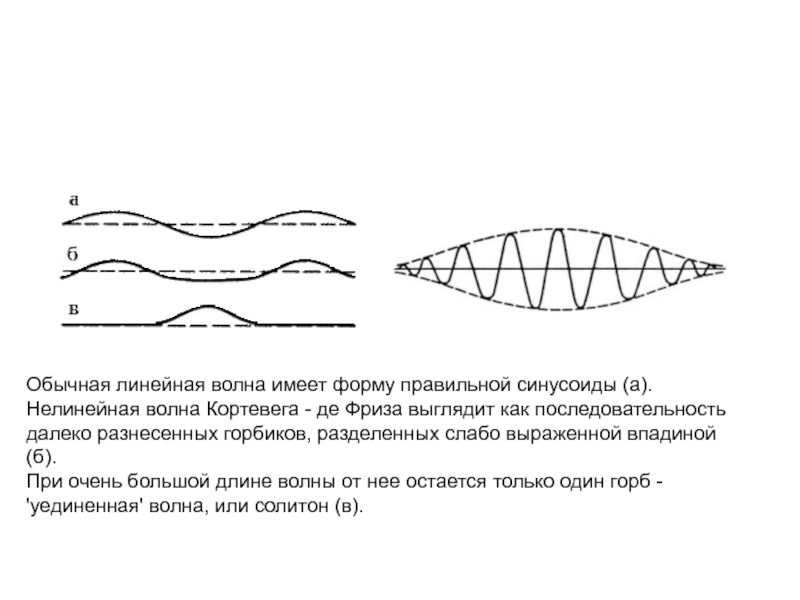
Обычная линейная волна имеет форму правильной синусоиды (а).
Нелинейная волна
Кортевега - де Фриза выглядит как последовательность далеко разнесенных горбиков,
разделенных слабо выраженной впадиной (б).
При очень большой длине волны от нее остается только один горб - 'уединенная' волна, или солитон (в).
Слайд 54
Но уединенный горб на воде можно представить в виде суммы
составляющих с разной длиной волны. Если среда обладает дисперсией, длинные
волны в ней побегут быстрее коротких, выравнивая крутизну фронта. В определенных условиях дисперсия полностью компенсирует влияние нелинейности, и волна будет долго сохранять свою первоначальную форму - образуется солитон
Слайд 55Так выглядит групповой солитон природе.
Это не 'уединенная' волна, а группа
из 14-20 волн (цуг, или волновой пакет) с одной длиной
волны, но с различной амплитудой, которая распространяется как одно целое, сохраняя форму огибающей. Самая высокая волна находится посередине группы; это и есть знаменитый 'девятый вал'.
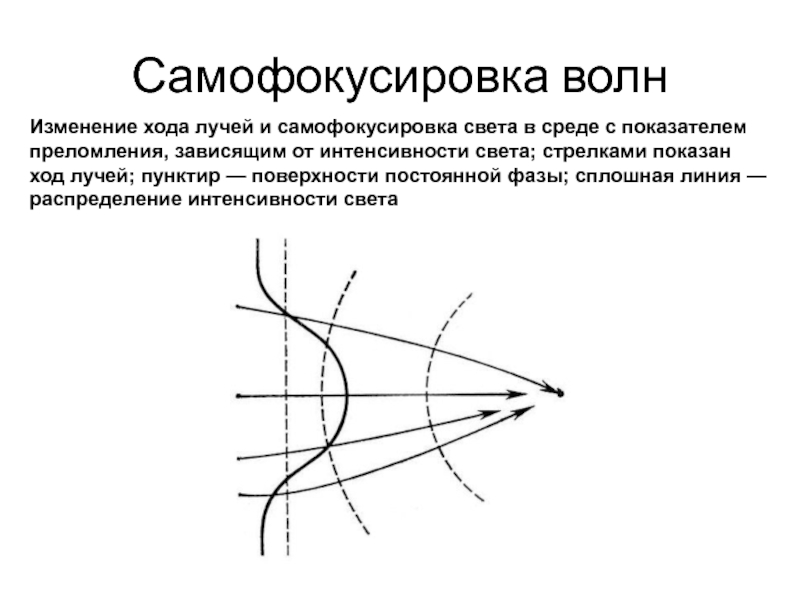
Слайд 56Самофокусировка волн
Изменение хода лучей и самофокусировка света в среде с
показателем преломления, зависящим от интенсивности света; стрелками показан ход лучей;
пунктир — поверхности постоянной фазы; сплошная линия — распределение интенсивности света
Слайд 57Самофокусировка света
В этом случае возникает так называемая нелинейная рефракция: в
поле ограниченного пучка однородная нелинейная среда: в поле ограниченного пучка
однородная нелинейная среда становится неоднородной; мощный луч электромагнитного излучения: в поле ограниченного пучка однородная нелинейная среда становится неоднородной; мощный луч электромагнитного излучения, проходя сквозь вещество, изменяет его свойства, что, в свою очередь, искривляет путь самого луча. Поэтому в зависимости от того, увеличивается или уменьшается показатель преломления в поле пучка (то есть от знака нелинейности), наблюдается концентрация энергии или, наоборот, ее рассеяние.
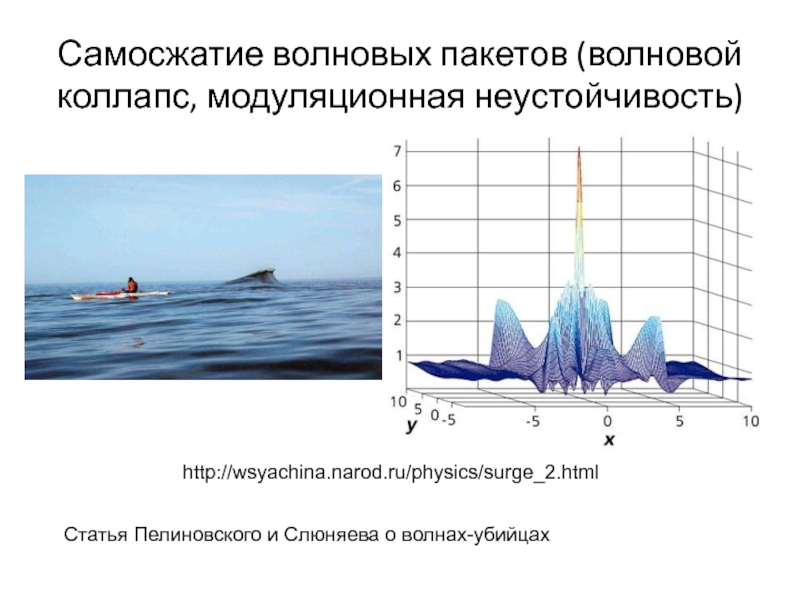
Слайд 58Самосжатие волновых пакетов (волновой коллапс, модуляционная неустойчивость)
http://wsyachina.narod.ru/physics/surge_2.html
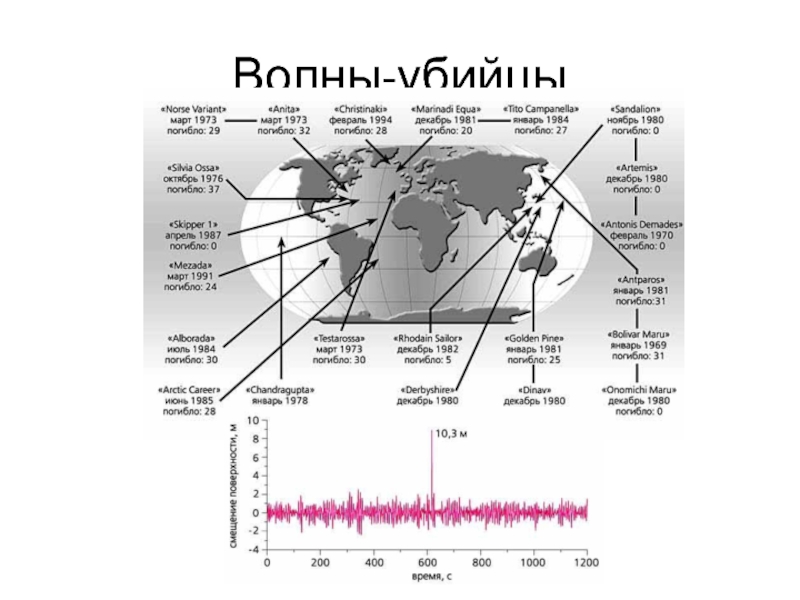
Статья Пелиновского и Слюняева
о волнах-убийцах