Обобщение и систематизация знаний по разделам стереометрии. Подготовка к ОКР

Задача . Из вершины треугольника АВС
восставлен перпендикуляр ВD к

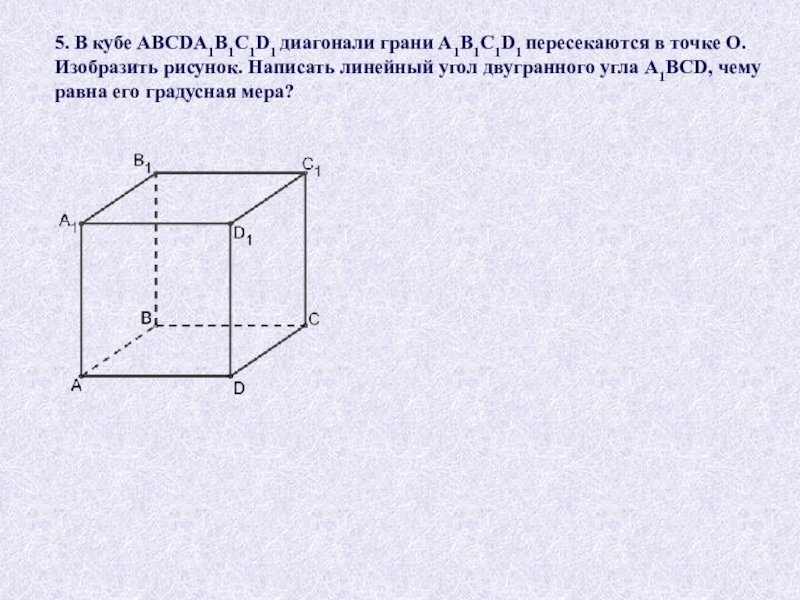
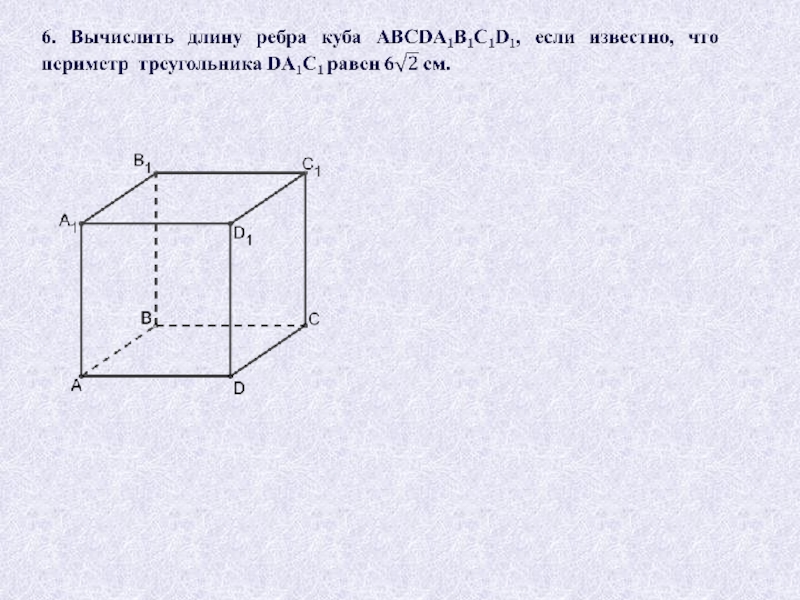
плоскости треугольника. Найдите расстояние от точки D до стороны АС,

А

В

С

D

15 см

20 см

7 см

9 см

Решение: Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из данной точки до прямой. Поэтому, из точки D опустим перпендикуляр DF на прямую АС.

F

По теореме о трёх перпендикулярах BF AC.

BF найдём из треугольника АВС.

Вычислим площадь треугольника АВС по формуле Герона.

p = (a+b+c)/2 = (15+20+7)/2 = 21,

S =

=

=

=

7·6 = 42 (см2).

S= AC·BF,

BF = 2·S/AC= 2·42 / 7 = 12 см.

12 см

Треугольник DFB – прямоугольный.

По теореме Пифагора DF2 = DB2 + BF2 ,

DF 2 = 81 + 144 = 225, DF = 15 см.

Ответ: 15 см.

15 см

лежат в одной плоскости.
Указать: 1) плоскости, которым принадлежит: а) прямая

Указать грань, в плоскости которой лежит прямая AD и точка

4. Дана четырехугольная пирамида SABCD. Точки K, P и T – середины ребер SD, AD и DC соответственно.

Какое из утверждений является верным:
А) PKT ∥ ASB,
Б) PKT ∥ BSC,
В) PKT ∥ ASC ?

О. Изобразить рисунок. Написать линейный угол двугранного угла А1ВСD, чему

см. Точки M, T, O и P – середины ребер

в двух перпендикулярных плоскостях, опущены перпендикуляры АС и ВD на

•

А

•

В

С

D

Дано: , А , В , АС CD, BD CD
АС = 6 м, ВD = 7 м, СD = 6 м.
Найти: АВ.

6 м

7 м

6 м

?

Решение: BCD – прямоугольный,

900

по теореме Пифагора ВС2 = СD2 + BD2,

ВС2 = 36 +49 = 85, ВС = м.

АВС – прямоугольный,

900

по теореме Пифагора АВ2 = АС2 + ВС2,

АВ2 = 36 + 85 = 121, АВ = 11 м.

Ответ : 11 м.

– соответственно середины ребер BC, DC, и AC тетраэдра DABC.