Слайд 1Обработка экспериментальных данных
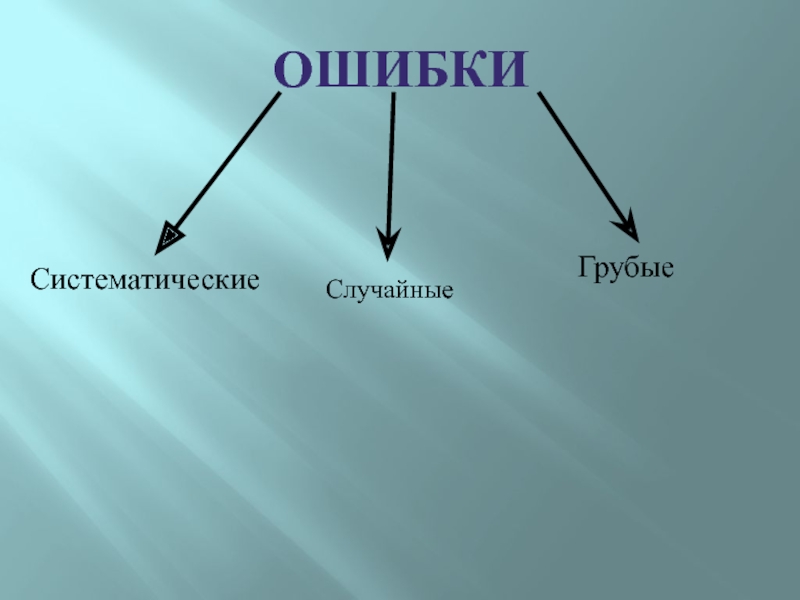
Слайд 2Ошибки
Систематические
Грубые
Случайные
Слайд 3Систематические ошибки –
обычно дают отклонение в одну сторону от
истинного значения измеряемой величины.
Причины появления:
условия эксперимента (влажность, температура
среды и др.),
дефект измерительного прибора,
его плохая регулировка (например, смещение указательной стрелки от нулевого положения) и т. д.
Методы устранения:
наладка аппаратуры
введение соответствующих поправок.
Слайд 4Случайные ошибки -
Имеют случайный (несистематический) характер, дают отклонения от
средней величины в ту или другую стороны при повторении измерений
и не могут быть устранены в эксперименте, как бы тщательно он ни проводился.
Причины появления:
Случайность
Методы устранения:
Статистическая обработка экспериментальных данных при повторении измерений достаточное число раз, поскольку с вероятностной точки зрения математическое ожидание случайной ошибки равно нулю.
Слайд 5Грубые ошибки -
явно искажают результат измерения; они чрезмерно большие и
обычно пропадают при повторении опыта.
Причины появления:
Случайность
Ошибка при проведении
опыта
Ошибка при записи результата
Методы устранения:
Повторное проведение опыта
Отбрасывание измерения с такими ошибками (в расчет при окончательной обработке результатов измерений эти точки не принимаются)
Слайд 6Найти φ(х)=?, такую что φ(xi)≈yi
Эмпирические формулы
Слайд 7График аппроксимационной (эмпирической) зависимости, вообще говоря, не проходит через заданные
точки (xi, yi), как в случае интерполяции.
Это приводит к
тому, что экспериментальные данные в некоторой степени сглаживаются, а интерполяционная формула повторила бы все ошибки, имеющиеся в экспериментальных данных.
Слайд 8Построение эмпирической формулы
подбора общего вида формулы
определения наилучших значений содержащихся в
ней параметров.
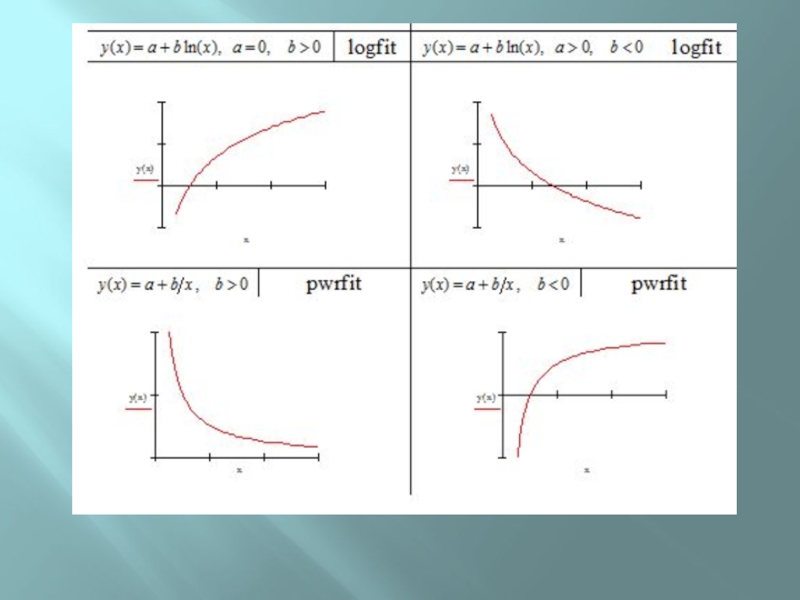
Слайд 9Общий вид формулы иногда известен из физических соображений.
Связь между напряжением,
u, и током, i, в резисторе определяется законом Ома:
u
= R∙ i ,
где R - активное сопротивление.
Задача сводится к определению одного неизвестного параметра R по известной линейной зависимости.
Слайд 10Если характер зависимости неизвестен, то вид эмпирической формулы может быть
произвольным.
Первоначально выбирается из геометрических соображений: экспериментальные точки наносятся на
график и примерно угадывается общий вид зависимости путем сравнения полученной кривой с графиками известных функций (многочлена, показательной или логарифмической функций и т. п.).
Слайд 11Линейная зависимость –
простейшая эмпирическая формула(легко просматривается после построения графика
данной экспериментальной зависимости)
Проверка линейности:
Если при этом k ≈ const, то
точки (xi, yi) расположены приблизительно на одной прямой
Слайд 12Приведение к линейной зависимости-
выравнивание данных
Для получения линейной зависимости
исходная формула
должна быть записана в виде
Слайд 14Возможность использования этой формулы для случая равноотстоящих точек xi можно
проверить путем вычисления вторых разностей:
При Δ2yi ≈ const квадратичный
трехчлен может быть выбран в качестве эмпирической формулы
Квадратный трехчлен
Слайд 15Определение параметров эмпирической зависимости.
Пусть тип эмпирической формулы выбран и
ее можно представить в виде
где φ - известная
функция, ai - неизвестные постоянные параметры, которые необходимо определить.
Слайд 16Определение параметров эмпирической зависимости.
Задача состоит в том, чтобы определить
такие значения параметров, при которых эмпирическая формула дает хорошее приближение
данной функции.
Здесь не ставится условие (как в случае интерполяции) совпадения опытных данных yi со значениями эмпирической функции в точках xi. Разность между этими значениями (отклонения) обозначают через εi
И задача нахождения наилучших значений параметров a0, a1,…, am сводится к некоторой минимизации отклонений εi. Существует несколько способов решения этой задачи.
Слайд 17Определение параметров эмпирической зависимости:
Метод выбранных точек
По заданным экспериментальным значениям на
координатной плоскости наносится система точек. Затем проводится простейшая плавная линия
(например, прямая), которая наиболее близко примыкает к данным точкам. На этой линии выбираются точки, которые, вообще говоря, не принадлежат исходной системе точек. Число выбранных точек должно быть равным количеству искомых параметров эмпирической зависимости. Координаты этих точек тщательно измеряются и используются для записи условия прохождения графика эмпирической функции через выбранные точки
Слайд 18Метод средних
Он состоит в том, что параметры эмпирической зависимости определяются
с использованием условия равенства нулю суммы отклонений во всех точках
xi:
Из одного уравнения нельзя однозначно определить все m+1 параметров. Однако, поскольку других условий нет, то имеющееся равенство путем группировки (достаточно произвольной) отклонений εi разбивается на систему, состоящую из m+1 уравнений.
Слайд 20Метод наименьших квадратов
Параметры a0, a1,…, am эмпирической формулы находят из
условия минимума функции S = S(a0,a1,…,am).
Поскольку здесь параметры a0, a1,…,
am - независимые переменные функции S, то ее минимум находится из условия равенства нулю частных производных по этим переменным:
…
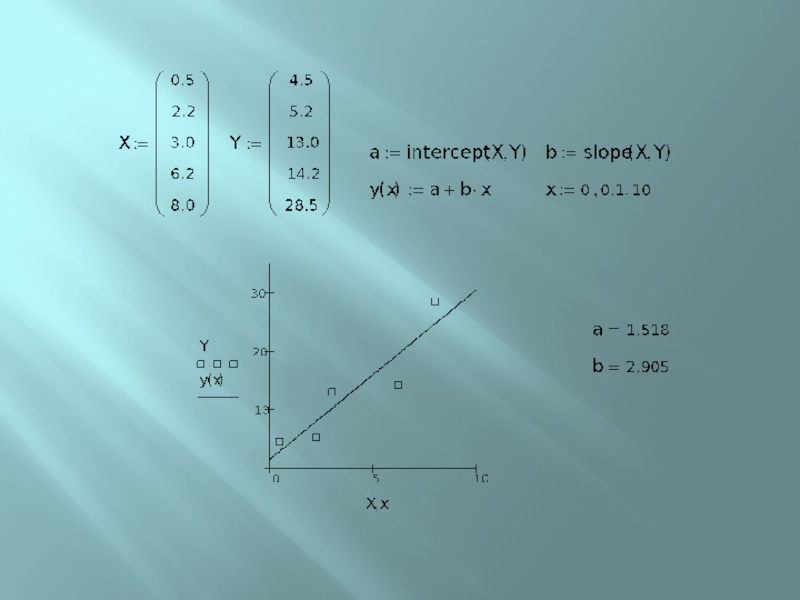
Слайд 21Линейная регрессия – вариант 1
Для нахождения коэффициентов уравнения прямой
используются
две функции
intercept (Х,Y)
slope (Х,Y).
Функция intercept (от англ. to
intercept – отсекать) возвращает значение коэффициента а.
Функция slope (англ. slope – наклон) – возвращает значение коэффициента b.
Слайд 23Линейная регрессия – вариант 2
Для нахождения коэффициентов уравнения прямой используется
одна функция:
line (Х,Y)
Функция возвращает вектор, первый элемент которого – значение
коэффициента а, в второй – значение коэффициента b, вычисленных по методу наименьших квадратов.
Пример использования этой функции :
Слайд 24Линейная регрессия – вариант3
Для нахождения коэффициентов уравнения прямой используется одна
функция:
medfit (Х,Y)
Функция возвращает вектор, первый элемент которого – значение коэффициента
а, в второй – значение коэффициента b, вычисленных по методу медиан.
Метод медиан довольно примитивен по сравнению с методом наименьших квадратов, и в большинстве случаев дает худший результат. Однако у метода медиан есть одно преимущество: он куда менее чувствителен к наличию в выборке промахов, то есть точек, полученных с недопустимо высокой погрешностью. Поэтому к нему нужно обращаться, если данные плохо ложатся на прямую.
Пример использования этой функции :
Слайд 25Коэффициента парной корреляции –
специальный показатель, количественно характеризующий на сколько
связь между парами точек близка к линейной
Чем меньше отличается абсолютная
величина r от единицы, тем ближе связь между парами точек к линейной.
Если коэффициент парной корреляции равен нулю, то переменные X и Y называют некоррелированными
Слайд 26Выборочный коэффициент корреляции
( выборочный линейный парный коэффициент корреляции К.
Пирсона)-
Если rn = 1, то связь линейна и a>0.
Если же rn = - 1, то связь линейна и a<0.
Коэффициент парной корреляции Пирсона вычисляют с помощью встроенной функции
corr(vx, vy),
vx и vy – вектора, содержащие анализируемые данные.
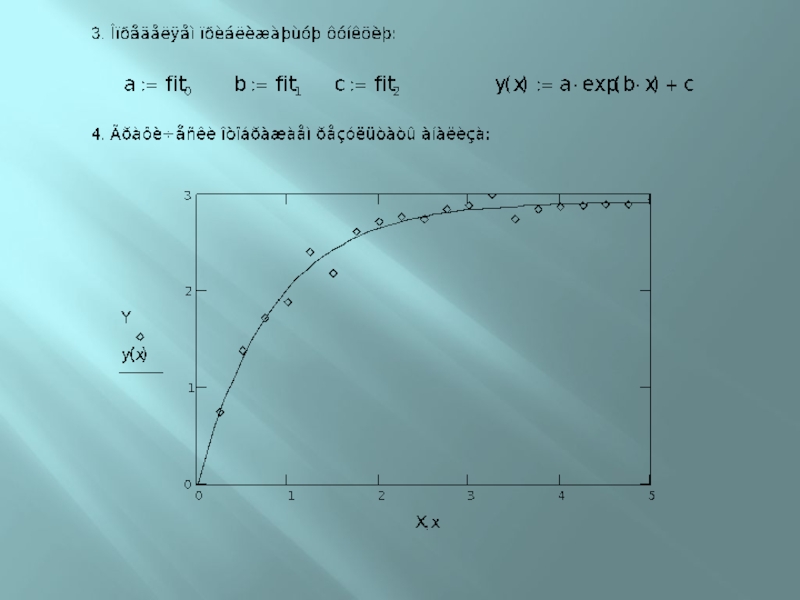
Слайд 27Определение коэффициентов нелинейных зависимостей
Вектора vx, vy содержат анализируемые данные
Вектору
vg, присваивают предполагаемые значения параметров a, b и с.
Слайд 32Аппроксимация обобщенным многочленом -
аппроксимирующую функцию выбирают в виде линейной
комбинации произвольных функций (обобщенного многочлена)
φ (х)– функции заданного вида (базисные
функции). Задача аппроксимации сводится к задаче нахождения коэффициентов с.
Слайд 33В пакете Mathcad задачу аппроксимации обобщенным многочленом решает функция
linfit(vx,
vy, F).
vx и vy – вектора, содержащие исходные данные
F –
вектор, каждый элемент которого является базисной функцией.
В качестве результата функция linfit возвращает вектор коэффициентов .
Слайд 36Аппроксимация обобщенным многочленом -
аппроксимирующую функцию выбирают в виде нелинейной
комбинации произвольных функций
Задача аппроксимации сводится к задаче нахождения
коэффициентов.
Из всех видов регрессии этот является наиболее универсальным, однако и наименее точной и трудной в использовании.
Огромное влияние на точность расчета неизвестных параметров с помощью нелинейной регрессии оказывает близость значений начального приближения коэффициентов к истинным их величинам.
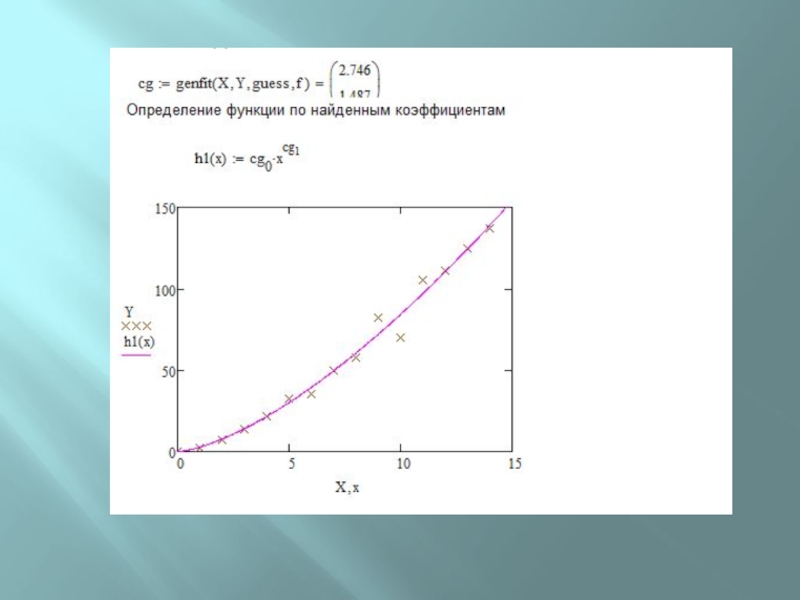
Слайд 37В пакете Mathcad задачу аппроксимации нелинейным многочленом решает функция
genfit(vx,
vy, g, F).
vx и vy – вектора, содержащие исходные данные
g — вектор приближений для неизвестных параметров.
F(x, g) — вектор-функция из n+1 элемента, где n — количество рассчитываемых параметров.
Первый элемент данной функции — это описывающая экспериментальную зависимость функция, параметры которой должны быть рассчитаны. Следующие n элементов вектор-функции F должны быть заполнены выражениями частных производных описывающей зависимость функции по искомым параметрам. Последовательность частных производных должна быть такой же, как последовательность приближений к соответствующим им параметрам в векторе g.
В качестве результата функция genfit возвращает вектор коэффициентов .
В отличие от всех остальных встроенных функций регрессии, точность результата вычислений с помощью genfit зависит от значения системной переменной TOL.
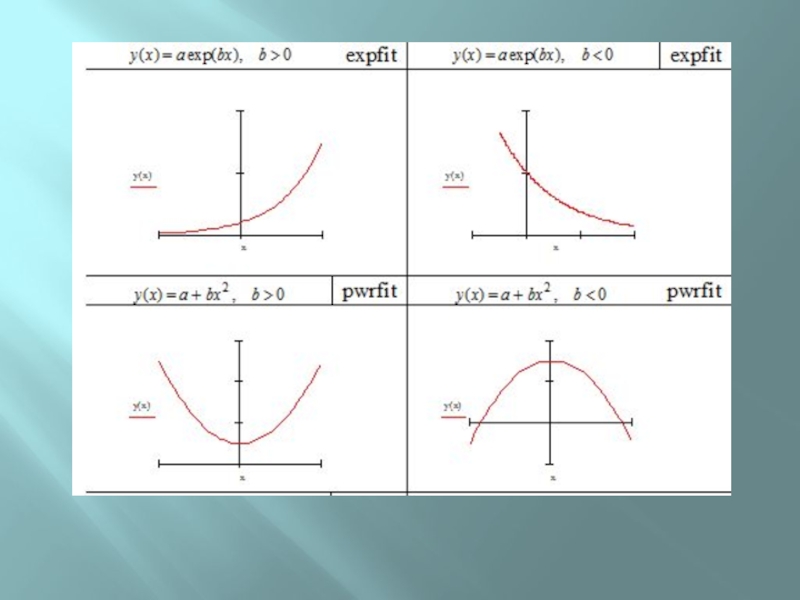
Слайд 40Аппроксимация степенным многочленом-
используется функция
regress(vx, vy, m )
vx и
vy – вектора, содержащие исходные данные;
m – степень многочлена
В качестве результата функция regress возвращает вектор, в котором первые три элемента содержат некоторые значения, используемые функцией interp, а остальные – значения коэффициентов полинома в порядке возрастания степеней, начиная со свободного члена.
Далее можно применить функцию interp.
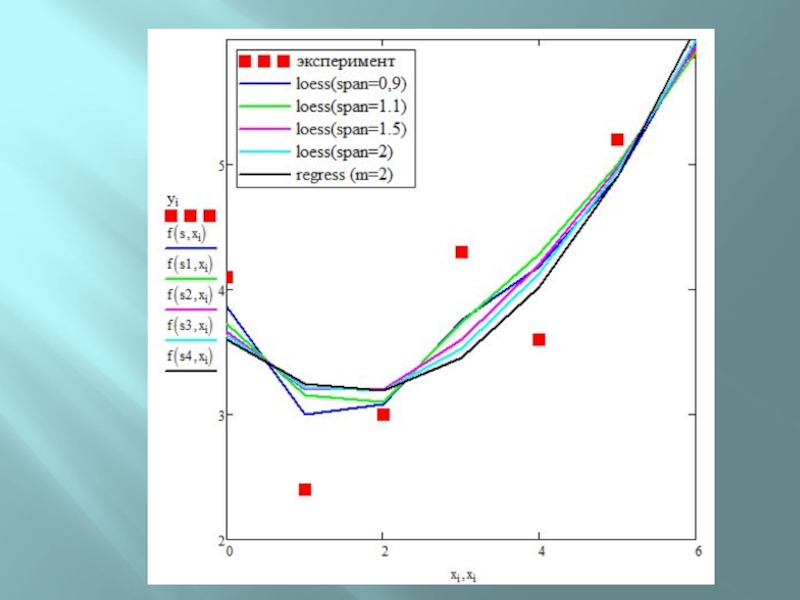
Слайд 41Регрессия отрезками полиномов -
регрессию сшивкой отрезков (участков) нескольких полиномов.
Для этого используется встроенная функция:
loess (х, у, span)
х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
у — вектор действительных данных значений того же размера;
span — параметр, определяющий размер отрезков полиномов (положительное число, хорошие результаты дает значение порядка span=0.75).
Функция возвращает вектор коэффициентов для построения регрессии данных отрезками полиномов.
Параметр span задает степень сглаженности данных. При больших значениях span регрессия практически не отличается от регрессии одним полиномом (span=2 дает почти тот же результат, что и приближение точек параболой).
Слайд 44Регрессия одним полиномом эффективна, когда множество точек выглядит как полином,
а регрессия отрезками полиномов оказывается полезной в противоположном случае.
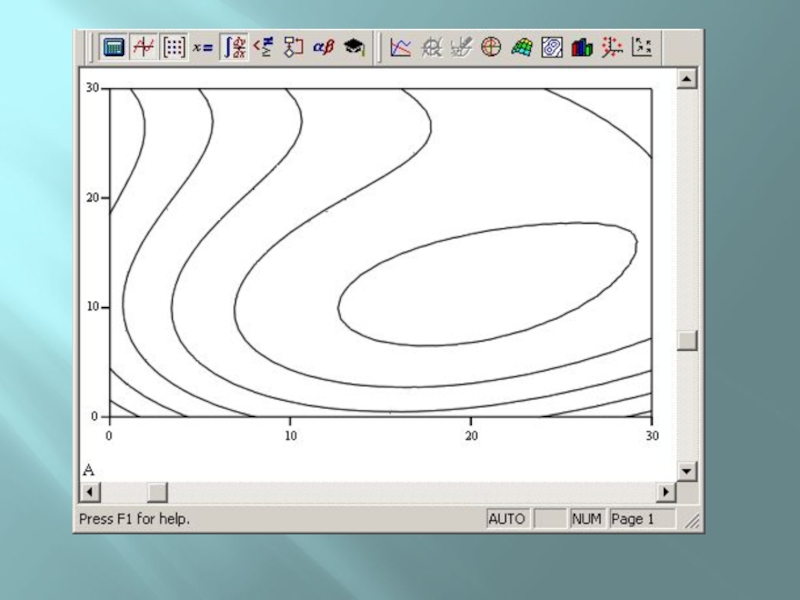
Слайд 45Двумерная полиномиальная регрессия:
regress (x,z,k) —
вектор коэффициентов для построения полиномиальной
регрессии данных.
loess (x, z, span) —
вектор коэффициентов
для построения регрессии данных отрезками полиномов.
interp(s,x,z,v) —
скалярная функция, аппроксимирующая данные выборки двумерного поля по координатам х и у кубическими сплайнами.
Слайд 46х — матрица размерности Nx2, определяющая пары значений аргумента (столбцы
соответствуют меткам х и у).
z — вектор действительных
данных размерности N.
k — степень полинома регрессии (целое положительное число).
span — параметр, определяющий размер отрезков полиномов.
s — вектор, созданный одной из сопутствующих функций loess или regress
v — вектор из двух элементов, содержащий значения аргументов х и у, для которых вычисляется интерполяция
Слайд 47Для построения регрессии не предполагается никакого предварительного упорядочивания данных (как,
например, для двумерной интерполяции, которая требует их представления в виде
матрицы NxN). В связи с этим данные представляются как вектор.
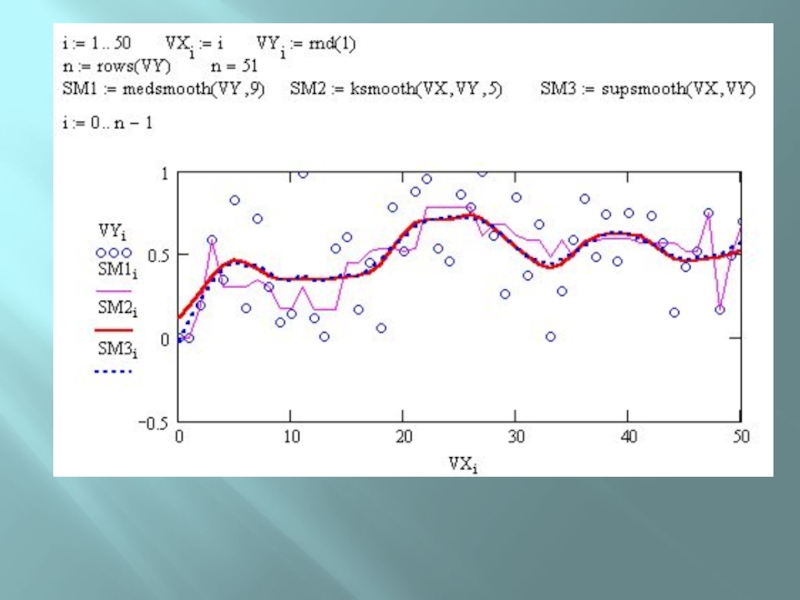
Слайд 50Сглаживание экспериментальных данных-
Сглаживание случайных составляющих погрешности экспериментов.
medsmooth(VY,n)
— для вектора
с m действительными числами возвращает m-мерный вектор сглаженных данных по методу скользящей
медианы, параметр n задает ширину окна сглаживания (n должно быть нечетным числом, меньшим m);
сглаживание алгоритмом «бегущих медиан»
Слайд 51ksmooth(VX, VY, b)
— возвращает n-мерный вектор сглаженных VY, вычисленных на основе распределения Гаусса. VX
и VY — n-мерные векторы действительных чисел. Параметр b (полоса пропускания) задает ширину
окна сглаживания ( b должно в несколько раз превышать интервал между точками по оси х );
сглаживание на основе функции Гаусса
Слайд 52supsmooth(VX, VY)
— возвращает n-мерный вектор сглаженных VY, вычисленных на основе использования процедуры
линейного сглаживания методом наименьших квадратов по правилу k-ближайших соседей с
адаптивным выбором k. VX и VY — n-мерные векторы действительных чисел. Элементы вектора VX должны идти в порядке возрастания;
локальное сглаживание адаптивным алгоритмом, основанное на анализе ближайших соседей каждой пары данных