Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Однофазные цепи синусоидального тока Астраханский государственный технический
Содержание
- 1. Однофазные цепи синусоидального тока Астраханский государственный технический
- 2. Содержание1. Основные теоретические сведения: основные понятия о
- 3. Основные теоретические сведенияПеременный электрический ток – это
- 4. Наиболее распространен переменный синусоидальный ток, являющийся синусоидальной
- 5. Мгновенное значения тока:i = Im sin (ωt
- 6. Аналогично выражаются мгновенные значения напряжения и ЭДС.u
- 7. Начальная фаза тока (ЭДС, напряжения) ψi, ψe,
- 8. Действующее значение переменного тока (ЭДС, напряжения) –
- 9. Представление синусоидальных величин вращающимися векторамиПродолжитьДля представления синусоидально
- 10. Представление синусоидальных величин вращающимися векторамиПродолжитьЕсли радиус-вектор вращать
- 11. В резистивном элементе происходит преобразование электрической энергии
- 12. Цепь переменного тока с резистивным элементомПродолжитьURm=R ImUR=R
- 13. Цепь переменного тока с индуктивным элементомИндуктивный элемент
- 14. Неразветвленная цепь переменного тока с резистивным и индуктивным элементамиПродолжить
- 15. Неразветвленная цепь переменного тока с резистивным и
- 16. Цепь с емкостным элементомЕмкостный элемент создает электрическое
- 17. Неразветвленная цепь переменного тока с резистивным и емкостным элементамиНапряжение на зажимах цепиДействующее значение напряженияРазность фазПродолжить
- 18. Неразветвленная цепь переменного тока с резистивным, индуктивным
- 19. Неразветвленная цепь переменного тока с резистивным, индуктивным
- 20. Мощности цепиАктивная мощность, Вт:P = U I
- 21. Резонанс напряженийВ неразветвленной цепи R-L-C при равенстве
- 22. Цепь с параллельными ветвями Рассмотрим разветвленную цепь,
- 23. Цепь с параллельными ветвями ПродолжитьАктивная проводимость цепи G равна арифметической сумме активных проводимостей параллельных ветвей:
- 24. Цепь с параллельными ветвями ПродолжитьРеактивная проводимость цепи
- 25. Цепь с параллельными ветвями ПродолжитьВ цепи можно
- 26. Компенсация реактивной мощностиПродолжитьИдея компенсации реактивной энергии индуктивного
- 27. Компенсация реактивной мощностиПродолжитьТок потребителя Iп отстает по
- 28. Компенсация реактивной мощностиПродолжитьНеобходимо включить параллельно индуктивному потребителю
- 29. Компенсация реактивной мощностиПродолжитьТок батареи конденсаторов IC, которая
- 30. Компенсация реактивной мощностиПродолжитьС другой стороны, ток IC=U/XC,
- 31. Практическое заданиеК однофазной цепи синусоидального тока напряжением
- 32. 1. Составление эквивалентной схемы замещения потребителейСхемы замещения
- 33. Для определения параметров схемы замещения рассматриваем каждую
- 34. Расчет двигателя:Сначала необходимо определить активную мощность, потребляемую
- 35. Расчет светильниковТак как мощность светильников одинакова, значит параметры светильников будут равны между собой:токиI1=I2=Pсв/U=60/220=0,273 АсопротивленияR1=R2=Pсв/I2=60/0,2732==805,056 ОмПродолжить
- 36. Свернем данную схему в ей эквивалентную методом
- 37. Определяем проводимости:реактивные:Bтр=XLтр/Zтр2=181,446/302,6132=0,001981 СмBдв=XLдв/Zдв2=112,714/148,3482= 0,005122 СмB1=B2=0Эквивалентная реактивная проводимость цепи: B=Bтр+Bдв=0,007103 СмЭквивалентная полная проводимость Продолжить
- 38. Определяем эквивалентные сопротивления всей цепи, индуктивность, ток и активную мощность:Zэкв=1/Y=1/0,0119=84,0336 ОмRэкв=G/Y2=67,1633 ОмXLэкв=B/Y2=50,1589 ОмLэкв=XLэкв/2πf=0,1597 ГнIэкв=U/Zэкв=2,618 АР=RэквIэкв2=460,3322 ВтПродолжить
- 39. Определяем:tg φп=tg φэкв=XLэкв/Rэкв==50,1589/67,1633=0,747По условию задачи tg φ=0.Продолжить2. Подключаем блок конденсаторов для снижения реактивной мощности
- 40. Параметры диаграммы:Iэкв=2,618 А
- 41. Iэкв=2,618 А
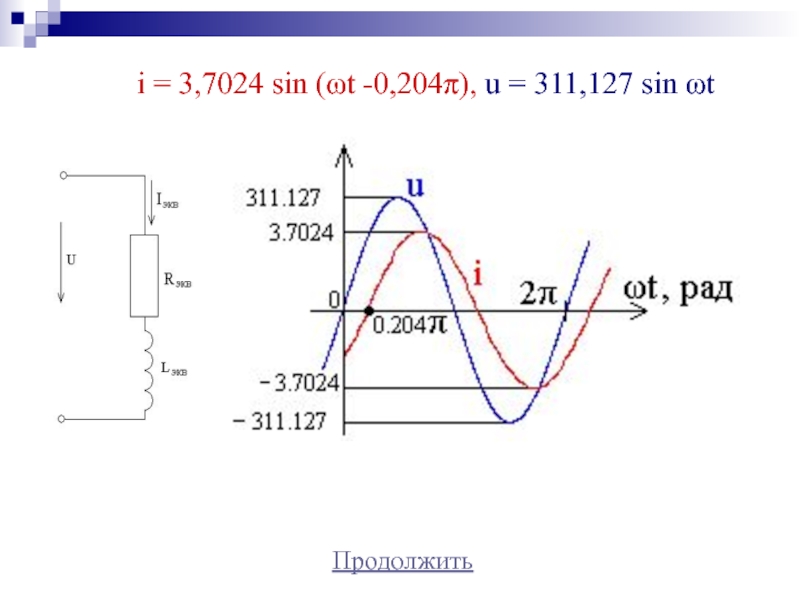
- 42. Продолжитьi = 3,7024 sin (ωt -0,204π), u = 311,127 sin ωt
- 43. IС=1,17 А
- 44. Продолжитьi = 1,65 sin (ωt +π/2), u = 311,127 sin ωt
- 45. Продолжитьi = 2,964 sin ωt , u
- 46. Задачи для самостоятельного решенияК однофазной цепи синусоидального
- 47. Слайд 47
- 48. Слайд 48
- 49. Слайд 49
- 50. Слайд 50
- 51. Закончить работу
- 52. ВекторыВектор – направленный отрезок, имеет определенную длину, направление указывает стрелка. ВекторВекторОтрезок AB Продолжить
- 53. Сложение векторовПравило параллелограмма: для векторов с общим
- 54. В нашем случае откладываем в качестве основного
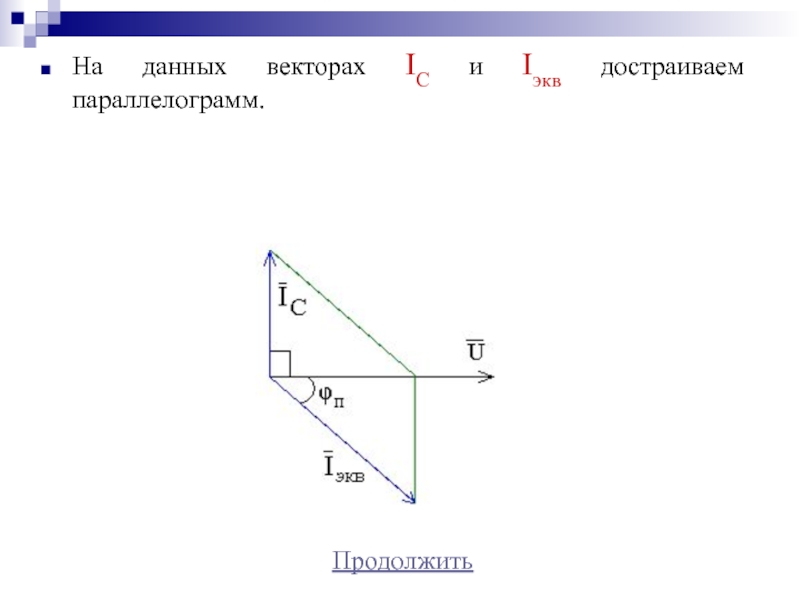
- 55. На данных векторах IС и Iэкв достраиваем параллелограмм.Продолжить
- 56. Тогда диагональ параллелограмма покажет вектор тока I
- 57. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Однофазные цепи синусоидального тока
Начать работу
Разработчик: ассистент Сенина О.А.
Научный консультант:
профессор Зайнутдинова Л.Х.
Слайд 2Содержание
1. Основные теоретические сведения: основные понятия о переменном токе, идеальные
и реальные элементы в цепи синусоидального тока.
2. Практическое задание: расчет
однофазной цепи синусоидального тока.3. Математическая поддержка: векторы и действия над ними.
4. Задачи для самостоятельного решения.
Продолжить
Слайд 3Основные теоретические сведения
Переменный электрический ток – это ток, изменяющийся с
течением времени.
Значение этой величины в рассматриваемый момент времени называется мгновенным
значением тока i.Продолжить
Слайд 4Наиболее распространен переменный синусоидальный ток, являющийся синусоидальной функцией времени.
Переменный синусоидальный
сигнал характеризуется:
периодом Т, который выражается в секундах (с),
частотой f
- величиной, обратной периоду, выражается в герцах (Гц).круговой частотой ω = 2πf (1/с).
Продолжить
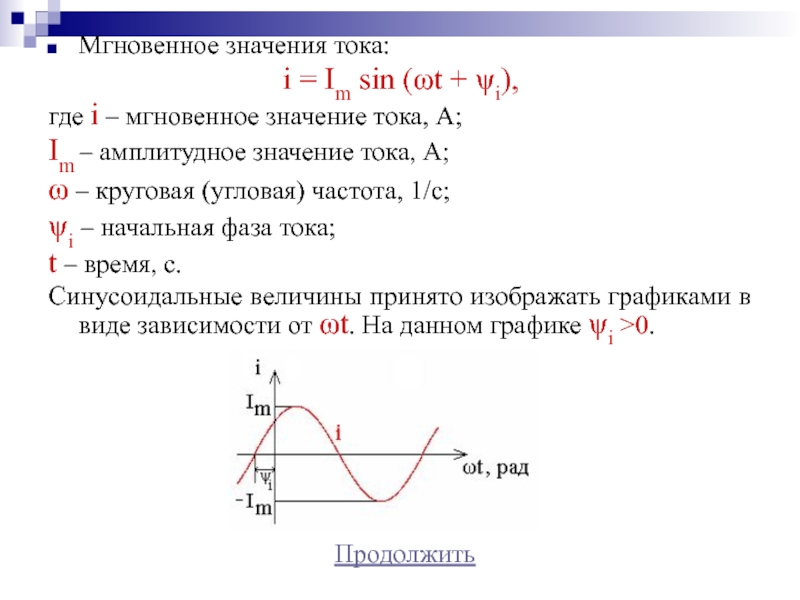
Слайд 5Мгновенное значения тока:
i = Im sin (ωt + ψi),
где i
– мгновенное значение тока, А;
Im – амплитудное значение тока,
А; ω – круговая (угловая) частота, 1/с;
ψi – начальная фаза тока;
t – время, с.
Синусоидальные величины принято изображать графиками в виде зависимости от ωt. На данном графике ψi >0.
Продолжить
Слайд 6Аналогично выражаются мгновенные значения напряжения и ЭДС.
u = Um sin
(ωt + ψu), e = Em sin (ωt +
ψe)Продолжить
На данных графиках ψu<0, ψe=0.
Слайд 7
Начальная фаза тока (ЭДС, напряжения) ψi, ψe, ψu – это
значение фазы в момент времени t = 0.
Разность начальных фаз
двух синусоидальных величин одной и той же частоты называют сдвигом фаз.Сдвиг фаз между напряжением и током определяется вычитанием начальной фазы тока из начальной фазы напряжения:
φ = ψu – ψi
Продолжить
Слайд 8Действующее значение переменного тока (ЭДС, напряжения) – это среднеквадратичное значение
переменного тока (ЭДС, напряжения) за период Т.
Если ток, ЭДС или
напряжение изменяются по синусоидальному закону, то действующее значение составляет :Продолжить
Слайд 9Представление синусоидальных величин вращающимися векторами
Продолжить
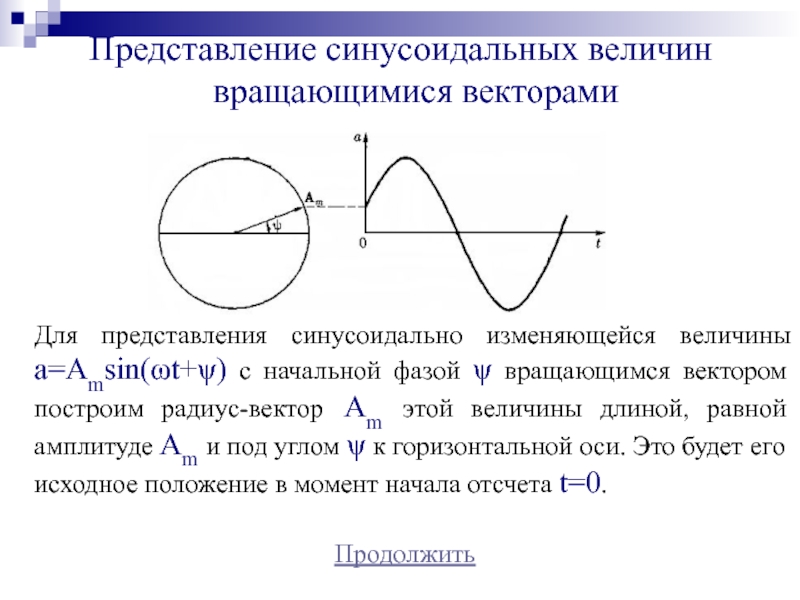
Для представления синусоидально изменяющейся величины a=Amsin(ωt+ψ)
с начальной фазой ψ вращающимся вектором построим радиус-вектор Am этой
величины длиной, равной амплитуде Am и под углом ψ к горизонтальной оси. Это будет его исходное положение в момент начала отсчета t=0.Слайд 10Представление синусоидальных величин вращающимися векторами
Продолжить
Если радиус-вектор вращать с постоянной угловой
скоростью
ω против направления движения часовой стрелки, то его проекция
на вертикальную ось будет равна Amsin(ωt+ψ) .Применение вращающихся векторов позволяет компактно представить на одном рисунке совокупность различных синусоидально изменяющихся величин одинаковой частоты.
Слайд 11В резистивном элементе происходит преобразование электрической энергии в тепловую.
Если приложено
синусоидально изменяющееся напряжение
u = Um sin ωt,
То, по закону Ома,
мгновенное значение тока в цепи:i = u/R = (Um/R) sin ωt = Im sin ωt
Продолжить
Цепь переменного тока с резистивным элементом
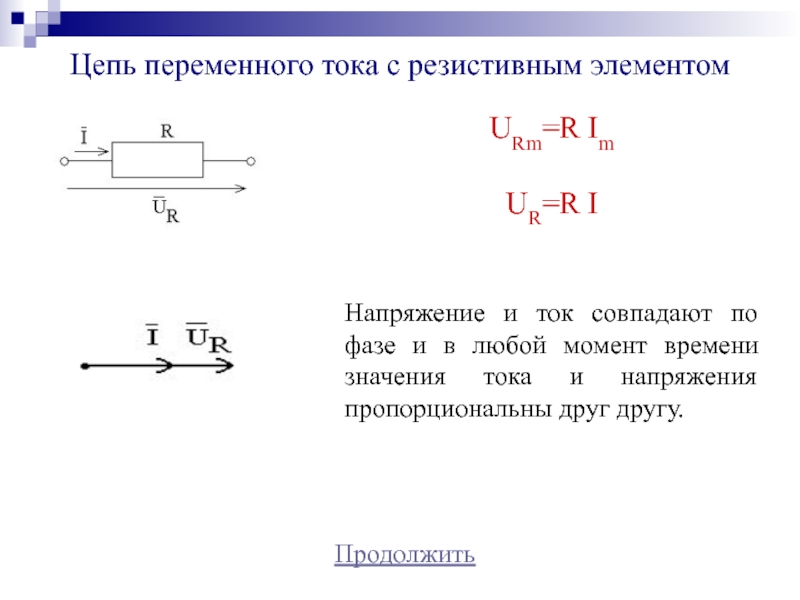
Слайд 12Цепь переменного тока с резистивным элементом
Продолжить
URm=R Im
UR=R I
Напряжение и ток
совпадают по фазе и в любой момент времени значения тока
и напряжения пропорциональны друг другу.Слайд 13Цепь переменного тока с индуктивным элементом
Индуктивный элемент создает магнитное поле.
Если
ток синусоидальный i = Im sin ωt, то тогда
u
= - e = L (d i/d t)= ULm cos ωt = ULm sin (ωt+π/2) Продолжить
ULm=ωL Im
Величина ХL =ωL – индуктивное сопротивление, Ом.
Напряжение на индуктивном элементе по фазе опережает ток на угол φ= π/2.
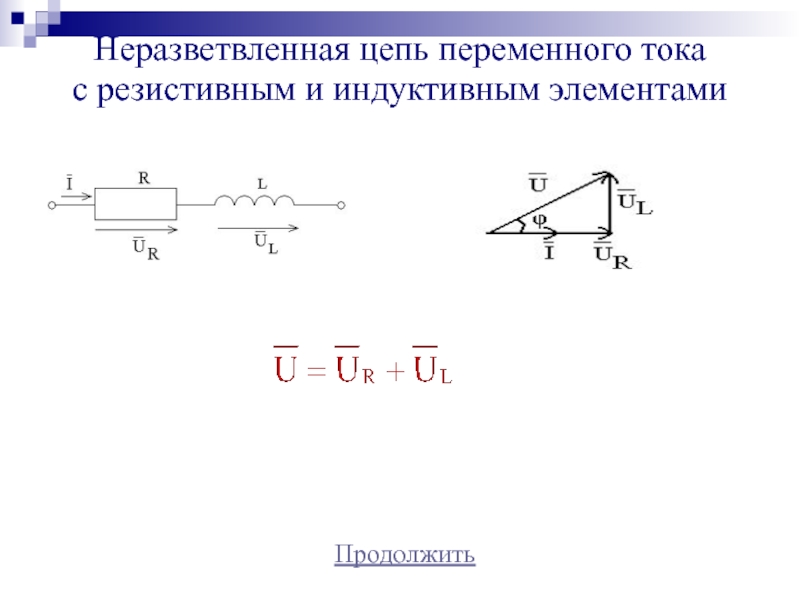
Слайд 15Неразветвленная цепь переменного тока
с резистивным и индуктивным элементами
Напряжение опережает
по фазе ток на угол φ:
Действующее значение напряжения U
(В): Полное сопротивление цепи Z (Ом):
Ток в цепи I (A):
Продолжить
Слайд 16Цепь с емкостным элементом
Емкостный элемент создает электрическое поле.
Если в цепи
проходит ток i=Imsin(ωt), i=dq/dt=C(duC/dt) , то тогда напряжение
то есть
напряжение отстает от тока на угол π/2.Действующее значение тока в цепи: I=U/XC, где ХС=1/(ωС) – емкостное сопротивление, Ом.
Продолжить
Слайд 17Неразветвленная цепь переменного тока
с резистивным и емкостным элементами
Напряжение на
зажимах цепи
Действующее значение напряжения
Разность фаз
Продолжить
Слайд 18Неразветвленная цепь переменного тока
с резистивным, индуктивным и емкостным элементами
Значение
напряжения на зажимах этой цепи равно сумме значений трех составляющих:
Действующее
значение Продолжить
Слайд 19Неразветвленная цепь переменного тока
с резистивным, индуктивным и емкостным элементами
Сдвиг
фаз между напряжением и током:
Продолжить
Х=XL-XC – реактивное сопротивление
Слайд 20Мощности цепи
Активная мощность, Вт:
P = U I cosφ = URI
= I2R
Реактивная мощность, вар:
Q = U I sinφ = (UL
– UC)I= I2XПолная мощность, ВА:
S = U I = I2Z =
Продолжить
Слайд 21Резонанс напряжений
В неразветвленной цепи R-L-C при равенстве реактивных сопротивлений XL=XC
наступает резонанс напряжений
Полное сопротивление принимает минимальное значение, равное активному сопротивлению:
Z = R.Падения напряжений UL и UC находятся в противофазе. При резонансе UL=UC равны между собой и приобретают максимальное значение. Ток в цепи имеет наибольшее значение I=U/R и совпадает по фазе с напряжением, то есть φ=0 и коэффициент мощности cos φ=1.
Продолжить
Слайд 22Цепь с параллельными ветвями
Рассмотрим разветвленную цепь, состоящую из двух
ветвей.
Ток неразветвленной части цепи может быть определен по закону Ома:
I = U/Z = UY, где Y-полная проводимость цепи.Продолжить
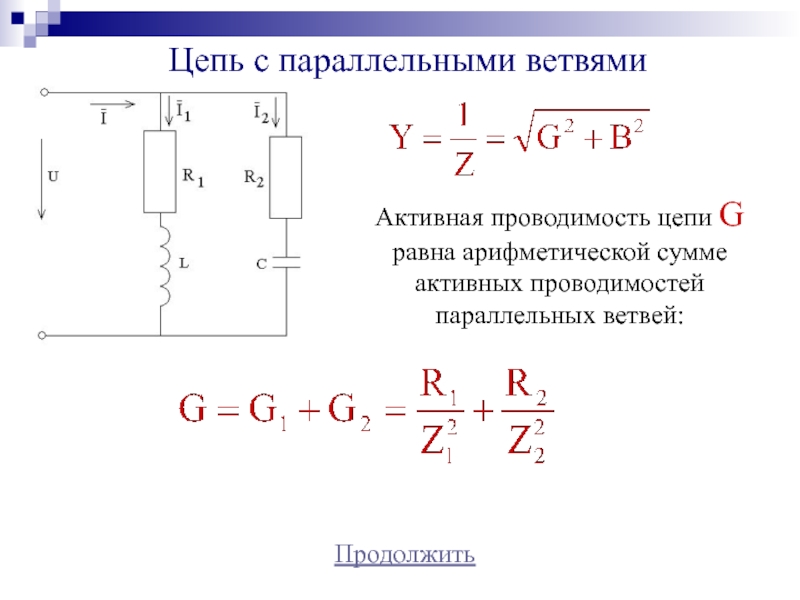
Слайд 23Цепь с параллельными ветвями
Продолжить
Активная проводимость цепи G равна арифметической
сумме активных проводимостей параллельных ветвей:
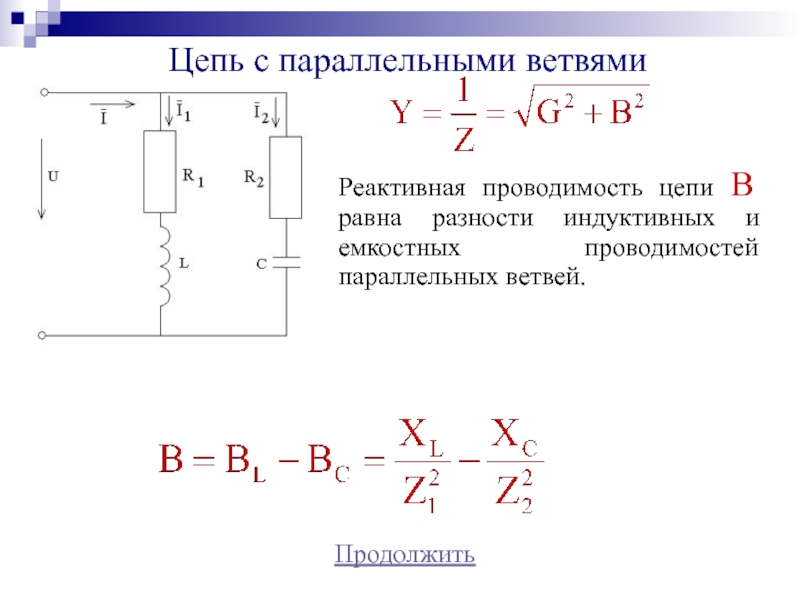
Слайд 24Цепь с параллельными ветвями
Продолжить
Реактивная проводимость цепи B равна разности
индуктивных и емкостных проводимостей параллельных ветвей.
Слайд 25Цепь с параллельными ветвями
Продолжить
В цепи можно получить резонанс токов
при условии равенства проводимостей BL=BC, тогда полная проводимость цепи Y=G.
Угол сдвига фаз φ между током I и напряжением U в неразветвленной части цепи равен нулю, так как реактивные составляющие токов в ветвях Ip1 и Ip2 равны между собой и находятся в противофазе.Цепь обладает только активной мощностью.
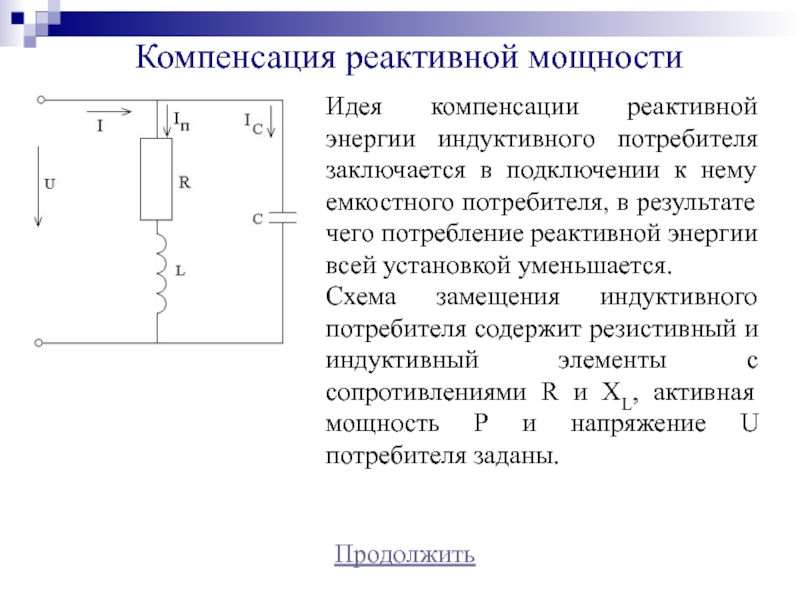
Слайд 26Компенсация реактивной мощности
Продолжить
Идея компенсации реактивной энергии индуктивного потребителя заключается в
подключении к нему емкостного потребителя, в результате чего потребление реактивной
энергии всей установкой уменьшается.Схема замещения индуктивного потребителя содержит резистивный и индуктивный элементы с сопротивлениями R и XL, активная мощность Р и напряжение U потребителя заданы.
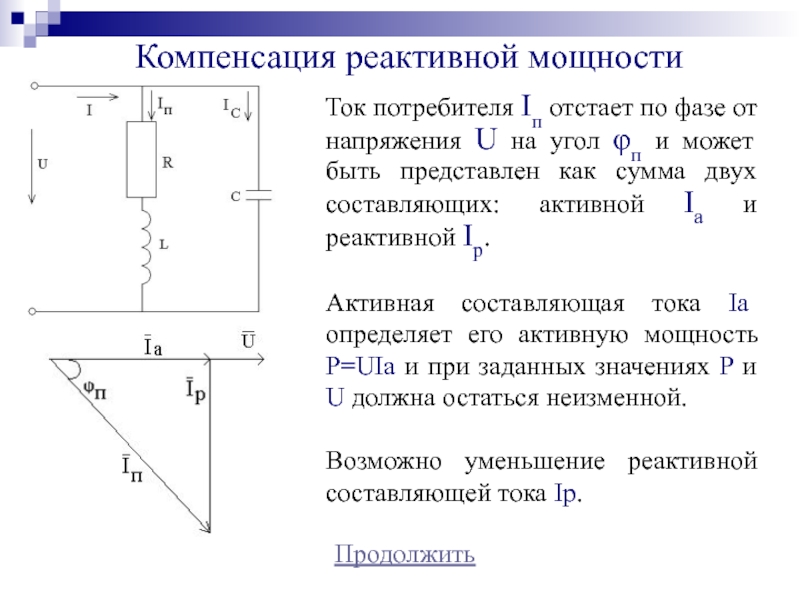
Слайд 27Компенсация реактивной мощности
Продолжить
Ток потребителя Iп отстает по фазе от напряжения
U на угол φп и может быть представлен как сумма
двух составляющих: активной Ia и реактивной Ip.Активная составляющая тока Ia определяет его активную мощность Р=UIa и при заданных значениях P и U должна остаться неизменной.
Возможно уменьшение реактивной составляющей тока Iр.
Слайд 28Компенсация реактивной мощности
Продолжить
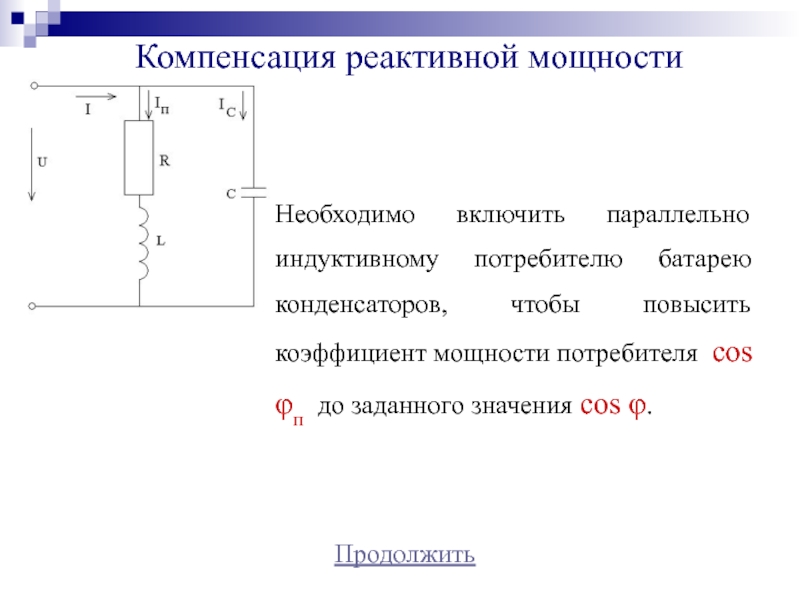
Необходимо включить параллельно индуктивному потребителю батарею конденсаторов, чтобы
повысить коэффициент мощности потребителя cos φп до заданного значения cos
φ.Слайд 29Компенсация реактивной мощности
Продолжить
Ток батареи конденсаторов IC, которая подключается параллельно индуктивному
потребителю, должен быть равен разности реактивных составляющих токов потребителя до
компенсации Ip и после компенсации Ip1.Слайд 30Компенсация реактивной мощности
Продолжить
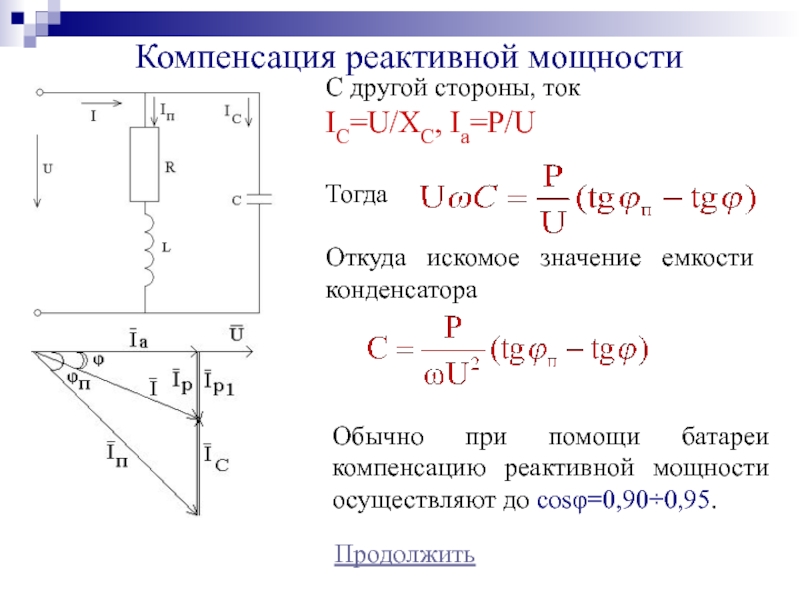
С другой стороны, ток
IC=U/XC, Ia=P/U
Тогда
Откуда искомое значение
емкости конденсатора
Обычно при помощи батареи компенсацию реактивной мощности осуществляют
до cosφ=0,900,95.Слайд 31Практическое задание
К однофазной цепи синусоидального тока напряжением Uном=220 В подключены
потребители:
однофазный трансформатор ОСМ-0,16, cos φ = 0,8;
однофазный асинхронный двигатель ДГ-2-0,14,
Рном=140Вт, η=66%, cos φ=0,65;светильники 60 Вт, 2 штуки.
Составить эквивалентную схему замещения потребителей и определить параметры ее элементов.
Рассчитать емкость батареи конденсаторов, которую нужно подключить к потребителю для снижения реактивной мощности до нуля.
Продолжить
Слайд 321. Составление эквивалентной схемы замещения потребителей
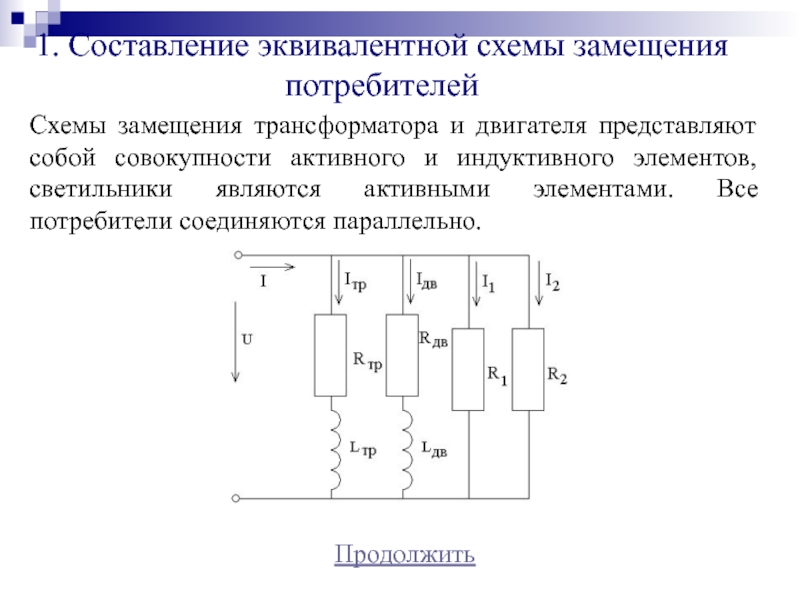
Схемы замещения трансформатора и двигателя
представляют собой совокупности активного и индуктивного элементов, светильники являются активными
элементами. Все потребители соединяются параллельно.Продолжить
Слайд 33Для определения параметров схемы замещения рассматриваем каждую из параллельных ветвей
цепи отдельно.
Расчет трансформатора:
Число 0,16 в маркировке трансформатора означает его полную
мощность, выраженную в киловольтамперах, то есть:Sтр=0,16 кВА =160 ВA Pтр=Sтрcosφтр=128 Вт
ток Iтр=Sтр/U=160/220=0,727 A
сопротивления: Zтр=U/Iтр=220/0,727=302,613 Ом
Rтр=Pтр/Iтр2=128/0,7272=242,182 Ом
Продолжить
индуктивность Lтр=ХL/2πf=0,578 Гн
Слайд 34Расчет двигателя:
Сначала необходимо определить активную мощность, потребляемую двигателем из сети:
Рдв=Рном/ηдв=140/0,66=212,121
Вт
полная мощность Sдв=Pдв/cosφдв=212,121/0,65=326,34 BA
ток Iдв=Sдв/U=326,34/220=1,483 A
сопротивления:
Zдв=U/Iдв=220/1,483=148,348 Ом
Rдв=Pдв/Iдв2=212,121/1,4832=96,45 Ом
Продолжить
индуктивность Lдв=ХLдв/2πf=0,359
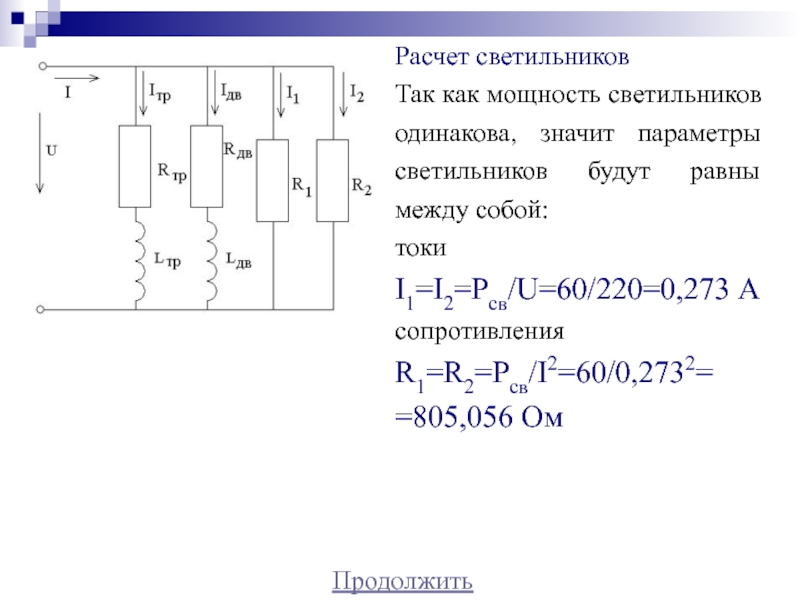
ГнСлайд 35Расчет светильников
Так как мощность светильников одинакова, значит параметры светильников будут
равны между собой:
токи
I1=I2=Pсв/U=60/220=0,273 А
сопротивления
R1=R2=Pсв/I2=60/0,2732=
=805,056 Ом
Продолжить
Слайд 36Свернем данную схему в ей эквивалентную методом активно-реактивных проводимостей
Определяем проводимости:
активные:
Gтр=Rтр/Zтр2=242,182/302,6132=0,002644
См
Gдв=Rдв/Zдв2=96,45/148,3482= 0,004383 См
G1=G2=1/R1=1/R2=1/805,056=0,001242 См
Эквивалентная активная проводимость цепи:
G=Gтр+Gдв+G1+G2=0,009511 См
Продолжить
Слайд 37Определяем проводимости:
реактивные:
Bтр=XLтр/Zтр2=181,446/302,6132=0,001981 См
Bдв=XLдв/Zдв2=112,714/148,3482= 0,005122 См
B1=B2=0
Эквивалентная реактивная проводимость цепи: B=Bтр+Bдв=0,007103 См
Эквивалентная
полная проводимость
Продолжить
Слайд 38Определяем эквивалентные сопротивления всей цепи, индуктивность, ток и активную мощность:
Zэкв=1/Y=1/0,0119=84,0336
Ом
Rэкв=G/Y2=67,1633 Ом
XLэкв=B/Y2=50,1589 Ом
Lэкв=XLэкв/2πf=0,1597 Гн
Iэкв=U/Zэкв=2,618 А
Р=RэквIэкв2=460,3322 Вт
Продолжить
Слайд 39Определяем:
tg φп=tg φэкв=XLэкв/Rэкв=
=50,1589/67,1633=0,747
По условию задачи
tg φ=0.
Продолжить
2. Подключаем блок конденсаторов
для снижения реактивной мощности
Слайд 40Параметры диаграммы:
Iэкв=2,618 А
IC=U/XC=U·2πfC=1,17 A
φп=φэкв=arctg(XLэкв/Rэкв)=arctg 0,747=36,8°
φ=0Масштаб выбираем произвольно, например 1см = 0,5 А
Продолжить
Построим векторную диаграмму токов
(повторить сложение векторов)
Таким образом, при полной компенсации реактивной мощности
I=Iэкв cos φпр=
=2,096 A
Слайд 41Iэкв=2,618 А
φп=36,8°
Продолжить
Покажем построение графиков мгновенных значений тока и напряжения
для эквивалентной схемыМгновенные значения токов и напряжения определяются:
i = Im sin (ωt + ψi)
u = Um sin (ωt + ψu)
φп= ψu – ψi=36,8°
Примем ψu=0, тогда ψi=-36,8°=
=-(36,8°/180°)π =-0,204π радиан
Слайд 43IС=1,17 А
φС= - 90°
Продолжить
Покажем построение графиков мгновенных значений для
емкостного элементаМгновенные значения токов и напряжения определяются:
i = Im sin (ωt + ψi)
u = Um sin (ωt + ψu)
Примем ψu=0, тогда
ψi= 90°= π/2 радиан
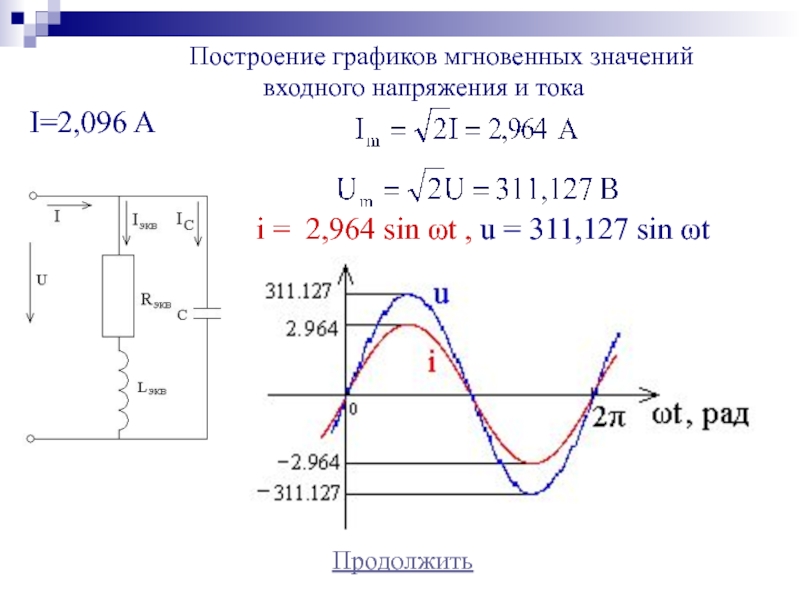
Слайд 45Продолжить
i = 2,964 sin ωt , u = 311,127 sin
ωt
Построение графиков мгновенных значений
входного напряжения и тока
I=2,096 AСлайд 46Задачи для самостоятельного решения
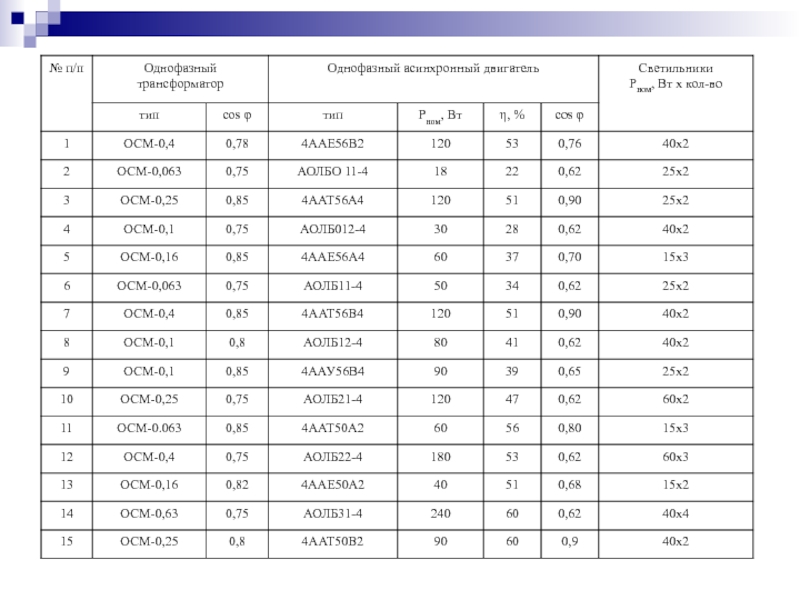
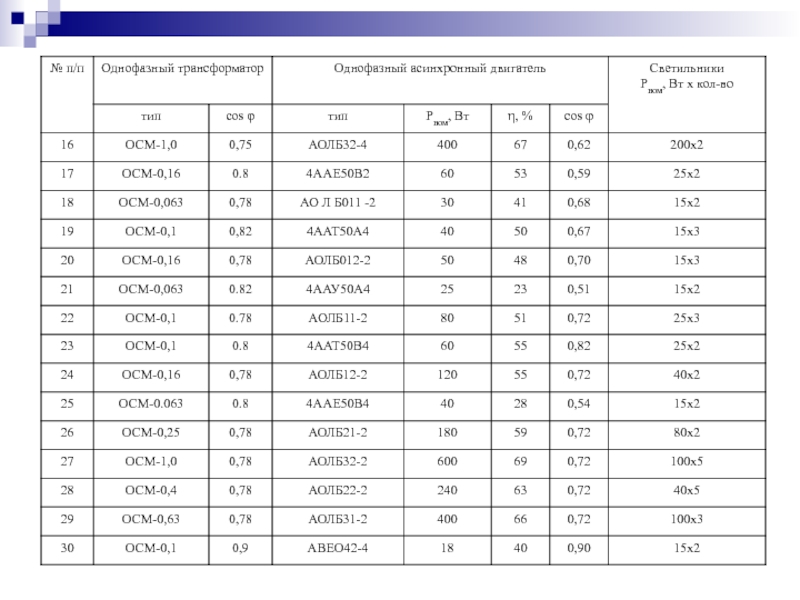
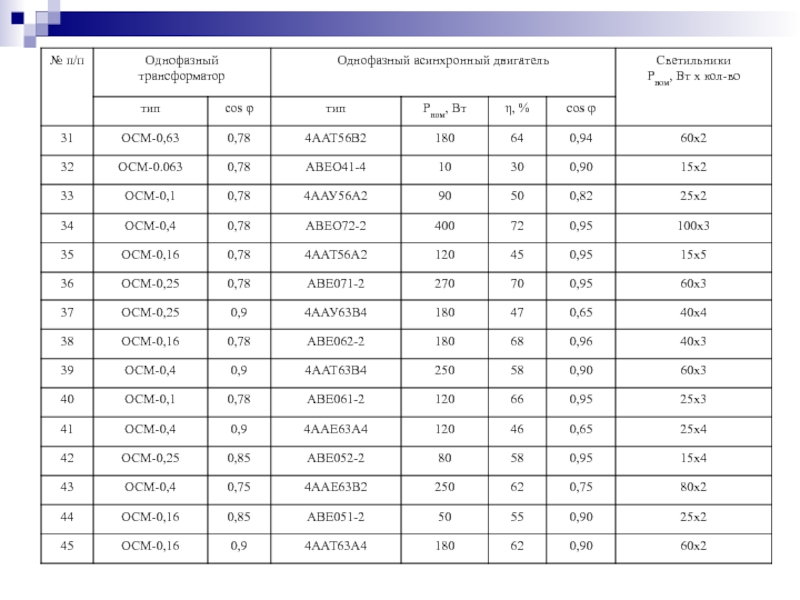
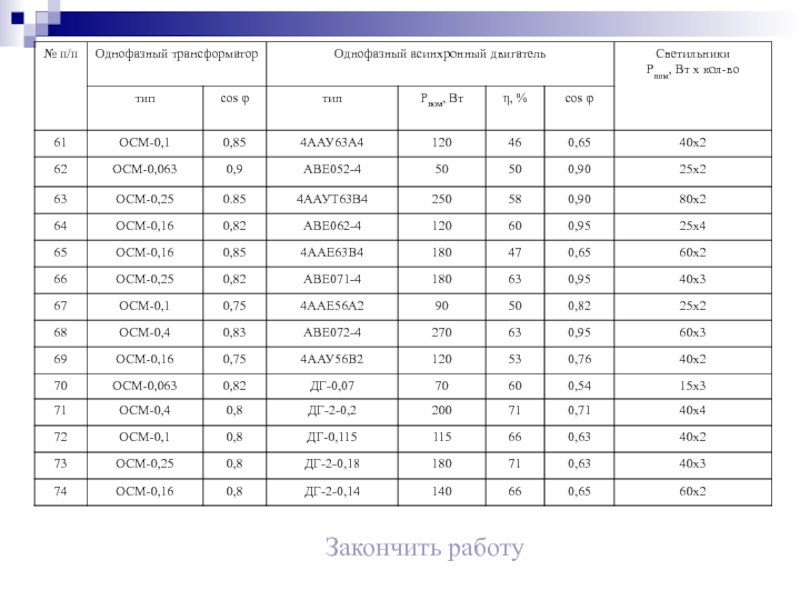
К однофазной цепи синусоидального тока напряжением Uн=220
В подключены потребители, типы и характеристики которых приведены в таблице.
Для
светильников cos φ=1.Составить эквивалентную схему замещения потребителей и определить параметры ее элементов.
Рассчитать емкость батареи конденсаторов, которую нужно подключить к потребителю для снижения реактивной мощности до нуля.
Слайд 52Векторы
Вектор – направленный отрезок, имеет определенную длину, направление указывает стрелка.
Вектор
Вектор
Отрезок AB
Продолжить
Слайд 53Сложение векторов
Правило параллелограмма: для векторов с общим началом их сумма
изображается диагональю параллелограмма, построенного на этих векторах.
Продолжить
Слайд 54В нашем случае откладываем в качестве основного вектор напряжения цепи.
Строим векторы тока в произвольно выбранном масштабе: ток IC на
конденсаторе опережает напряжение на угол 90°, ток Iэкв отстает на угол 36,8° (положительное направление угла – против часовой стрелки):Продолжить
Слайд 56Тогда диагональ параллелограмма покажет вектор тока I – сумму векторов
IС и Iэкв .
При правильном расчете и построении векторы тока
I и напряжения U должны совпадать по направлению (φ=0).Вернуться в задачу