Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы прикладной теории упругости
Содержание
- 1. Основы прикладной теории упругости
- 2. Напряженное состояние в точке
- 3. Напряженное состояние в точкеПравила знаковНормальные растягивающие напряжения
- 4. Тензор напряженийЗакон парности касательных напряженийНа двух взаимно-перпендикулярных
- 5. Главные напряжения
- 6. Инварианты тензора напряженийКонтроль правильности определения главных напряжений
- 7. Деформированное состояние в точке
- 8. Главные деформации
- 9. Объемная деформация– размеры параллелепипедаРазмеры параллелепипеда после деформации
- 10. Уравнения связи деформаций и перемещений в декартовой системе координатОдна из проекций параллелепипедадо деформации и после деформации
- 11. Уравнения Коши (геометрические уравнения)
- 12. Уравнения неразрывности деформацийЗависимости между составляющими деформаций в одной плоскости
- 13. Уравнения неразрывности деформацийЗависимости между составляющими деформаций в разных плоскостях
- 14. Уравнения неразрывности деформацийВсе 6 компонентов деформаций произвольно
- 15. Обобщенный закон Гука
- 16. Обобщенный закон Гука
- 17. Обобщенный закон Гука
- 18. Основные гипотезы предельных состоянийПредельное НС – НС,
- 19. Коэффициент запаса прочностиПод коэффициентом запаса понимается число,
- 20. 1. Гипотеза наибольшего нормального напряженияВ качестве критерия
- 21. 2. Гипотеза наибольших линейных деформацийОтрыв материала по
- 22. 3. Гипотеза максимальных касательных напряженийОбразование остаточных деформаций
- 23. 4. Гипотеза энергии формоизмененияВнутренняя потенциальная энергия =
- 24. 4. Гипотеза энергии формоизмененияГипотеза применима к оценке
- 25. Теория прочности МораОбщепризнанной в настоящее время является теория прочности Мора
- 26. Дифференциальные уравнения равновесия в декартовой системе координат
- 27. Дифференциальные уравнения равновесия в декартовой системе координат
- 28. Дифференциальные уравнения равновесия в декартовой системе координатX
- 29. Дифференциальные уравнения равновесия в декартовой системе координат
- 30. Дифференциальные уравнения равновесия в декартовой системе координатСтатические уравнения равновесия
- 31. Формулировка линейной задачи теории упругостиСтатические (или динамические)уравнения равновесия
- 32. Формулировка линейной задачи теории упругостиГеометрические уравнения
- 33. Формулировка линейной задачи теории упругостиФизические уравнения
- 34. Запись основных соотношений теории упругости в цилиндрической
- 35. Запись основных соотношений теории упругости в цилиндрической системе координат (осесимметричная задача)Физические соотношения:
- 36. Запись основных соотношений теории упругости в цилиндрической системе координат (осесимметричная задача)Уравнения равновесия:
- 37. Математические модели решения задач теории упругости1. Одномерные
- 38. Методы решения линейной задачи теории упругостиМетод перемещенийиз
- 39. Метод перемещений
- 40. Уравнения Коши (геометрические уравнения)
- 41. Метод сил (модель ПНС)Уравнения равновесия:Геометрические уравнения
- 42. Метод сил (модель ПНС)Физические уравнения
- 43. Метод сил (модель ПНС)Используем уравнение неразрывности
- 44. Метод сил (модель ПНС)
- 45. Метод сил (модель ПНС)Уравнение Леви
- 46. Метод сил (модель ПНС)Система дифференциальных уравнений
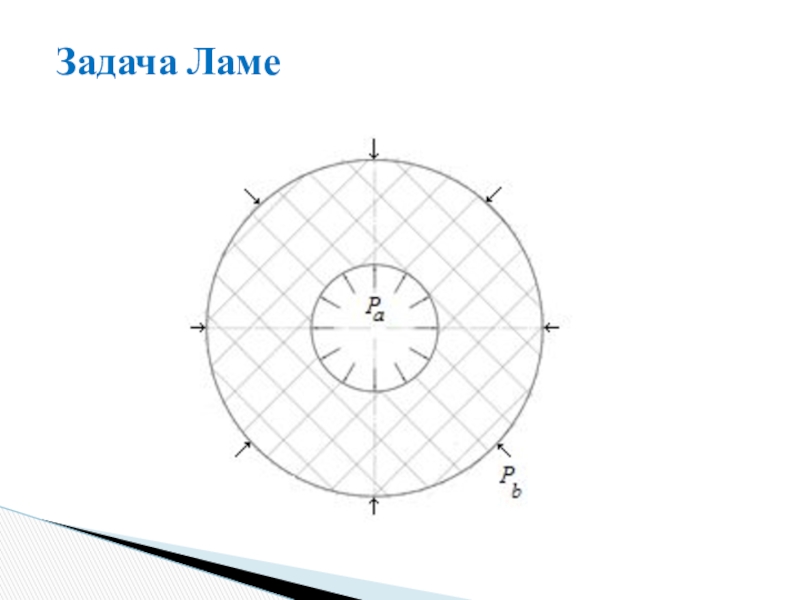
- 47. Задача Ламе
- 48. НДС прочноскрепленного заряда при действии внутреннего давления
- 49. Благодарю за внимание!
- 50. Скачать презентанцию
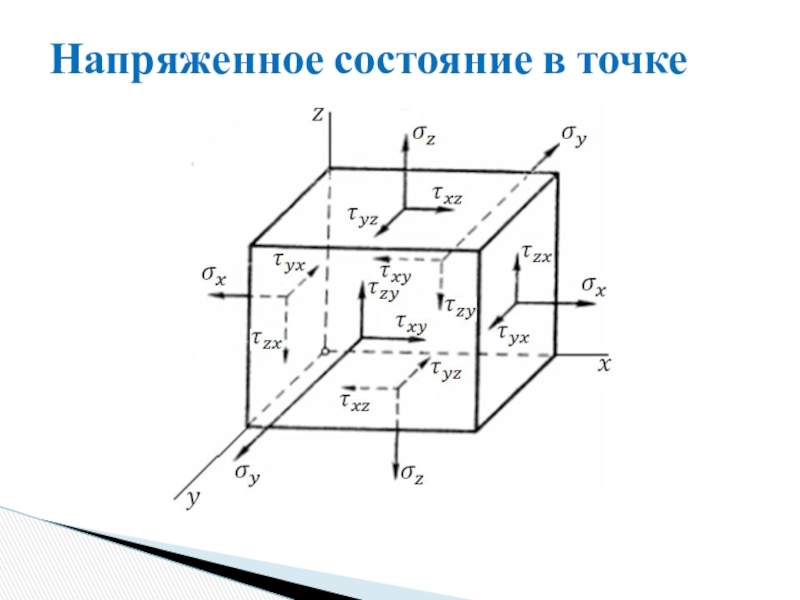
Напряженное состояние в точке
Слайды и текст этой презентации
Слайд 3Напряженное состояние в точке
Правила знаков
Нормальные растягивающие напряжения считаются положительными, сжимающие
– отрицательными.
координат, если направление растягивающих нормальных напряжений по той же площадке совпадает с положительным направлением соответствующей оси координат.Слайд 4Тензор напряжений
Закон парности касательных напряжений
На двух взаимно-перпендикулярных площадках составляющие касательных
напряжений, перпендикулярных общему ребру, равны и направлены обе либо к
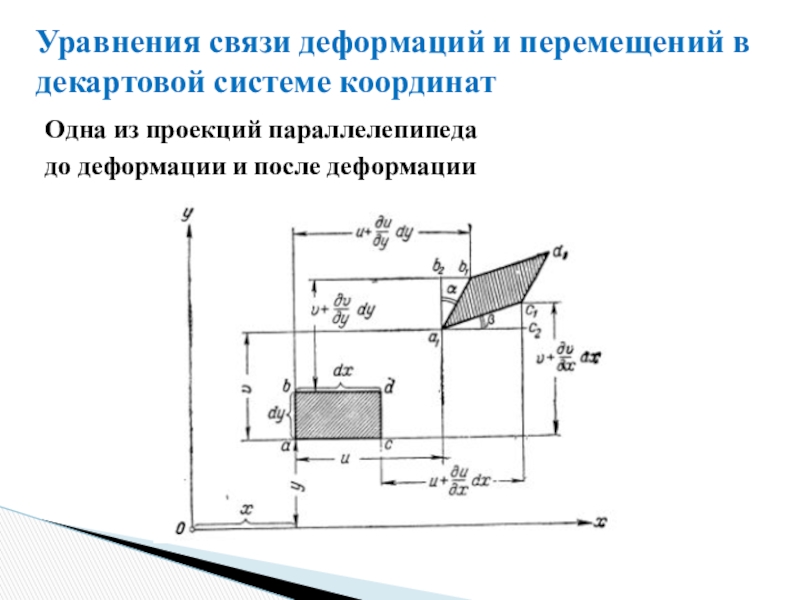
ребру, либо от ребра.Слайд 10Уравнения связи деформаций и перемещений в декартовой системе координат
Одна из
проекций параллелепипеда
до деформации и после деформации
Слайд 12Уравнения неразрывности
деформаций
Зависимости между составляющими деформаций в одной плоскости
Слайд 13Уравнения неразрывности
деформаций
Зависимости между составляющими деформаций в разных плоскостях
Слайд 14Уравнения неразрывности
деформаций
Все 6 компонентов деформаций произвольно задавать нельзя. Между ними
существуют зависимости, приведенные выше.
Физический смысл уравнений
Если, задаваясь деформациями, не учитывать
уравнения неразрывности деформаций, и для каждого параллелепипеда, на которые мысленно разбито тело, назначить 6 независимых составляющих деформаций, то из отдельных таких деформированных параллелепипедов нельзя собрать непрерывного деформированного тела.Тело, сплошное и непрерывное до деформации остается сплошным и непрерывным после деформации
Слайд 18Основные гипотезы
предельных состояний
Предельное НС – НС, при котором происходит качественное
изменение свойств материала – переход от одного механического состояния в
другое:пластический материал – возникновение заметных остаточных деформаций;
хрупкий материал – начало разрушения материала.
Предельное НС может рассматриваться как характеристика свойств материала.
Трудность создания теории предельных состояний – недостаточность наших представлений о внутренних процессах, происходящих в материале.
Задача решается в основном путем анализа и обобщения экспериментальных данных.
2 направления в ТПС
на основе гипотез;
феноменологический подход (применяется при описании явлений, детальный механизм которых недостаточно ясен: физика – закон всемирного тяготения; геология – при описании закономерностей расположения залежей полезных ископаемых).
Слайд 19Коэффициент запаса прочности
Под коэффициентом запаса понимается число, показывающее, во сколько
раз следует увеличить все компоненты НС, чтобы оно стало предельным.
Если
в двух НС коэффициенты запаса равны, то такие НС называются равноопасными.При растяжении
При сжатии
Слайд 201. Гипотеза наибольшего нормального напряжения
В качестве критерия прочности берется величина
наибольшего нормального напряжения 1.
Два других главных не учитываются.
Слайд 212. Гипотеза наибольших линейных деформаций
Отрыв материала по плоскости можно рассматривать
как результат нарушений межмолекулярных сил сцепления вследствие увеличения расстояния между
молекулами.Была выдвинута гипотеза использовать в качестве ПС наибольшую линейную деформацию.
Эта гипотеза получила довольно широкое распространение, однако детальная проверка обнаружила в ней ряд существенных недостатков.
Слайд 223. Гипотеза максимальных касательных напряжений
Образование остаточных деформаций в металлах происходит
сдвигом частиц друг относительно друга.
Поэтому критерием перехода от упругого состояния
в пластическое являются наибольшие касательные напряжения в точке.Это означает, что пластические деформации начинают образовываться тогда, когда максимальные касательные напряжения достигают некоторого предельного значения
Пластичные материалы – удовлетворительные результаты.
Недостатки – для материалов, имеющих различные механические характеристики на растяжение и сжатие.
Слайд 234. Гипотеза энергии формоизменения
Внутренняя потенциальная энергия = энергия изменения объема
+ энергия формоизменения.
В основе перехода из упругого состояния в
пластическое учитывается только энергия формоизменения.Слайд 244. Гипотеза энергии формоизменения
Гипотеза применима к оценке ПС пластичных материалов
и дает результаты менее удовлетворительные для материалов, неодинаково сопротивляющихся растяжению
и сжатию.Гипотезы 3 и 4 являются основными гипотезами ПС и сохраняют свое значение до настоящего времени.
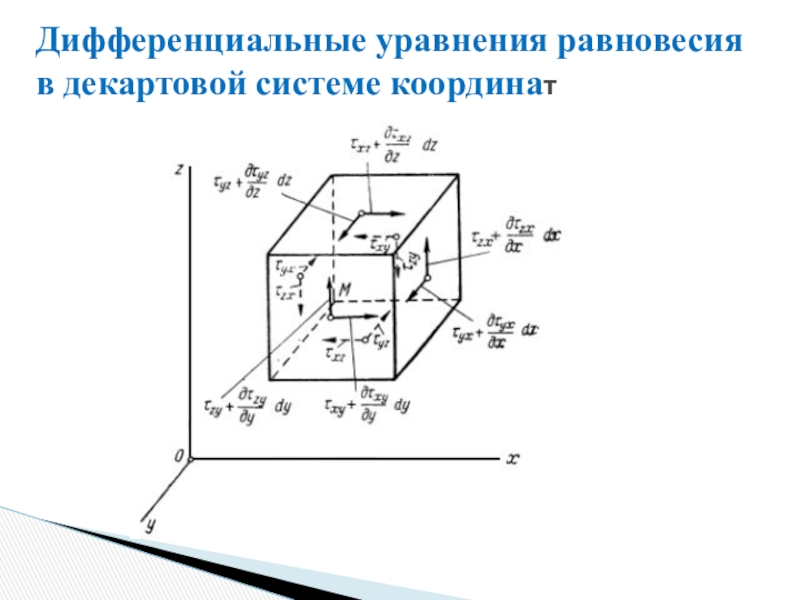
Слайд 28Дифференциальные уравнения равновесия
в декартовой системе координат
X – проекция на ось
x объемной силы, отнесенной к единице массы
Слайд 30Дифференциальные уравнения равновесия
в декартовой системе координат
Статические уравнения равновесия
Слайд 31Формулировка линейной задачи
теории упругости
Статические (или динамические)
уравнения равновесия
Слайд 34Запись основных соотношений теории упругости в цилиндрической системе координат (осесимметричная
задача)
r, θ, z – цилиндрические координаты;
u, w – перемещения.
Геометрические соотношения:
Слайд 35Запись основных соотношений теории упругости в цилиндрической системе координат (осесимметричная
задача)
Физические соотношения:
Слайд 36Запись основных соотношений теории упругости в цилиндрической системе координат (осесимметричная
задача)
Уравнения равновесия:
Слайд 37Математические модели решения задач теории упругости
1. Одномерные модели
Растяжение/сжатие, чистый сдвиг,
кручение
2. Плоские модели
плоское напряженное состояние;
плоское деформированное состояние;
обобщенная плоская деформация.
3. Осесимметричная
модель4. Плоские осесимметричные модели
осесимметричное ПНС;
осесимметричное ПДС.
5. Трехмерная модель
Слайд 38Методы решения линейной задачи
теории упругости
Метод перемещений
из уравнений обобщенного закона Гука
выразить напряжения через деформации;
выразить напряжения через перемещения, используя геометрические соотношения;
подставить
эти соотношения в уравнения равновесия.Метод сил: основные неизвестные – напряжения.
Смешанный метод: за основные неизвестные приняты некоторые из перемещений и некоторые из напряжений.