Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Особенности решения тригонометрических уравнений
Содержание
- 1. Особенности решения тригонометрических уравнений
- 2. Знать определение тригонометрического уравнения, их виды и
- 3. Тригонометрическая окружность
- 4. Арккосинус0π1-1arccos(-а)Арккосинусом числа а называется такое число (угол)
- 5. Арксинус
- 6. Арктангенс0arctgа = tАрктангенсом числа а называетсятакое число
- 7. Арккотангенсух0πarcctg а = tАрккотангенсом числа а называетсятакое
- 8. Формулы корней простейших тригонометрических уравнений1.cost = а
- 9. Формулы корней простейших тригонометрических уравнений2. sint
- 10. Формулы корней простейших тригонометрических уравнений3. tgt =
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
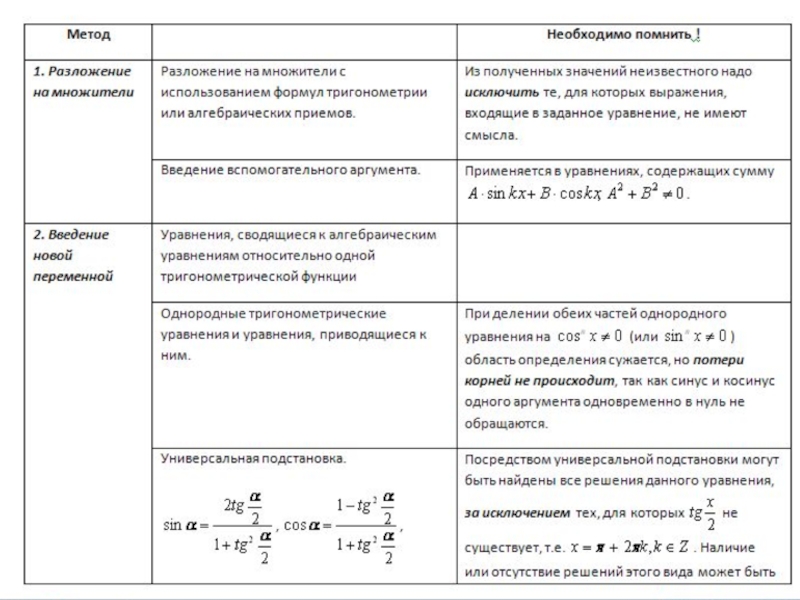
- 14. 1.Сводимые к квадратным Решаются методом введения новой
- 15. 2) Однородные уравнения второй степени:Решаются делением на
- 16. Формулы.
- 17. 1 способ. Путем введения вспомогательного аргумента.
- 18. Поскольку функция
- 19. 2 способ. С помощью универсальной подстановки.
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. 4 способ Возведение обеих частей равенства в квадрат и приведение к однородному уравнению.
- 24. Слайд 24
- 25. Простые советы.Увидел квадрат – понижай степень.Увидел произведение – делай сумму. Увидел сумму – делай произведение.
- 26. 1.Потеря корней: делим на g(х).опасные формулы (универсальная
- 27. Способы отбора корней Арифметический способАлгебраический способГеометрический способФункционально-графический способ
- 28. Спасибо завнимание!
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Особенности решения тригонометрических уравнений
Учитель математики
МАОУ лицей № 48 г.Краснодара
Гаврилова
Маргарита Петровна
Слайд 2Знать определение тригонометрического уравнения, их виды и способы решения;
Иметь представление
о методах решения тригонометрических уравнений;
Уметь применять тригонометрические формулы для упрощения
выраженийЗнать способы, позволяющие сделать отбор корней при решении тригонометрических уравнений;
Уметь распознавать вид тригонометрического уравнения, требующих для своего решения отбора корней;
Уметь правильно изображать на единичной окружности точки, соответствующие значениям тригонометрических функций, и в случае «табличных» значений уметь определять значения аргументов этих функций;
Владеть аппаратом способов решения тригонометрических уравнений, требующих для своего решения отбора корней.
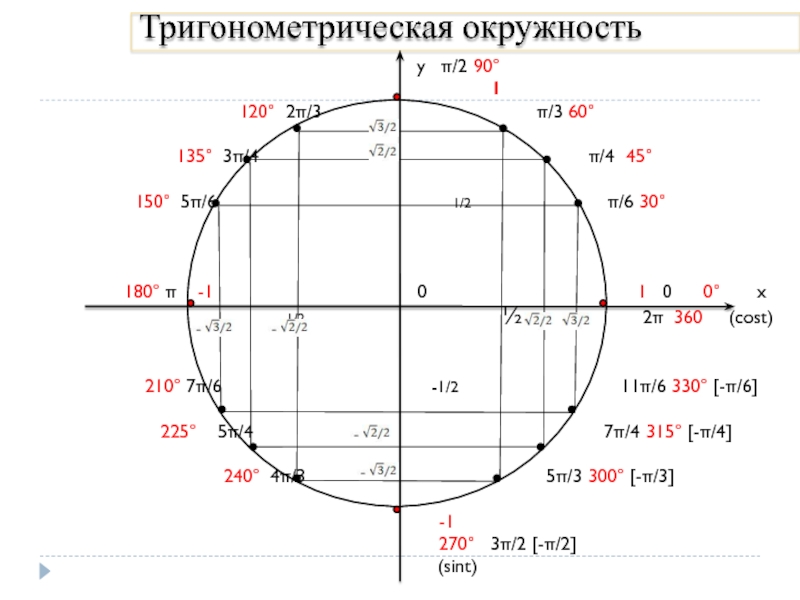
Слайд 3Тригонометрическая окружность
у π/2 90°
1
120° 2π/3 π/3 60°
135° 3π/4 π/4 45°
150° 5π/6 1/2 π/6 30°
180° π -1 0 1 0 0° x
-1/2 ½ 2π 360 (cost)
210° 7π/6 -1/2 11π/6 330° [-π/6]
225° 5π/4 7π/4 315° [-π/4]
240° 4π/3 5π/3 300° [-π/3]
-1
270° 3π/2 [-π/2]
(sint)
Слайд 4Арккосинус
0
π
1
-1
arccos(-а)
Арккосинусом числа а называется
такое число (угол) t из [0;π],
что
cos t = а.
Причём, | а |≤ 1.
arccos(-
а) = π- arccos аПримеры:
1)arccos(-1)
= π
2)arccos( )
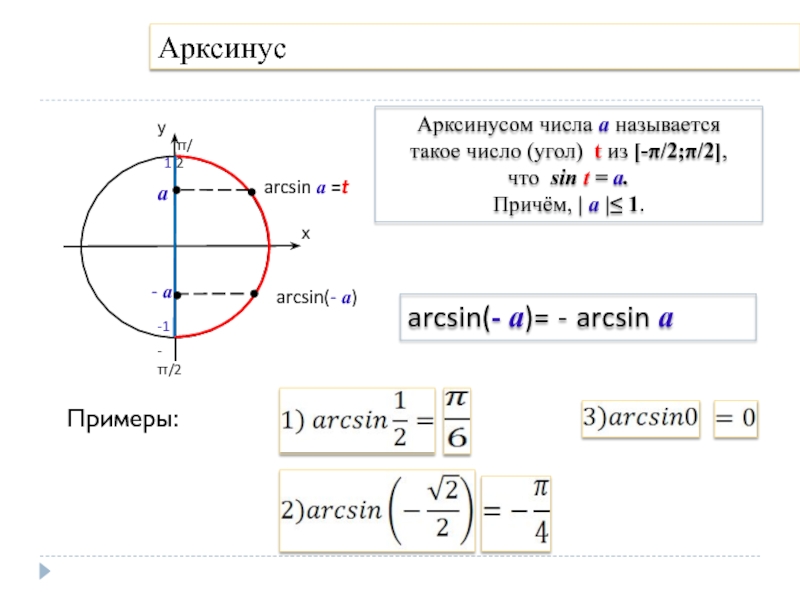
Слайд 5Арксинус
Примеры:
а
- а
arcsin(- а)= - arcsin а
Арксинусом числа а называется
такое число (угол) t из [-π/2;π/2],
что sin t = а.
Причём, | а |≤ 1.
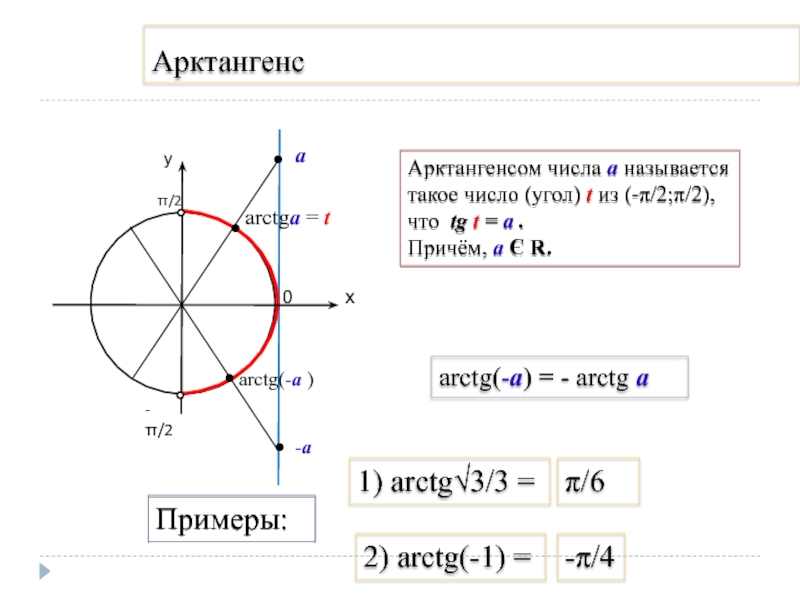
Слайд 6Арктангенс
0
arctgа = t
Арктангенсом числа а называется
такое число (угол) t из
(-π/2;π/2),
что tg t = а .
Причём, а Є R.
arctg(-а)
= - arctg а-а
arctg(-а )
Примеры:
1) arctg√3/3 =
π/6
2) arctg(-1) =
-π/4
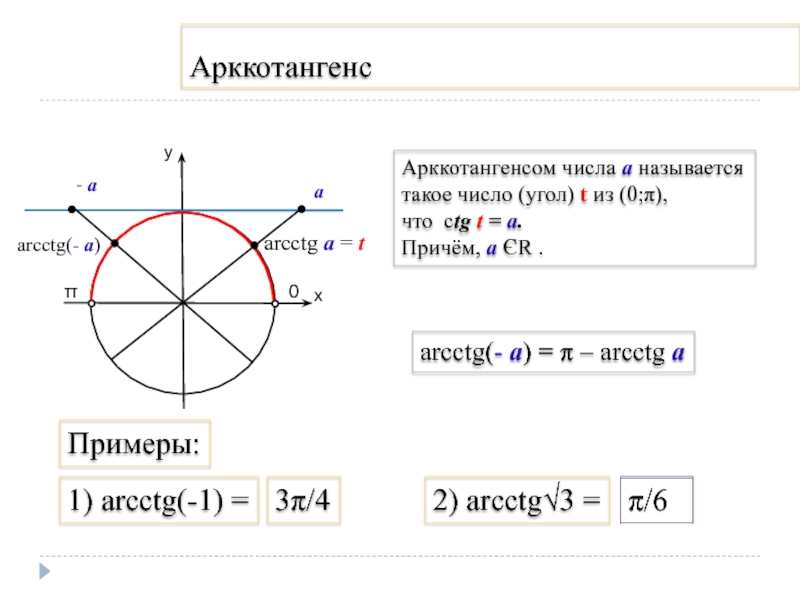
Слайд 7Арккотангенс
у
х
0
π
arcctg а = t
Арккотангенсом числа а называется
такое число (угол) t
из (0;π),
что ctg t = а.
Причём, а ЄR .
arcctg(- а) = π – arcctg а
- а
arcctg(- а)
1) arcctg(-1) =
Примеры:
3π/4
2) arcctg√3 =
π/6
Слайд 8Формулы корней простейших тригонометрических уравнений
1.cost = а , где |а|
≤ 1
или
Частные случаи
1) cost=0
t = π/2+πk‚ kЄZ
2) cost=1
t = 2πk‚ kЄZ 3) cost = -1
t = π+2πk‚ kЄZ
Слайд 9Формулы корней простейших тригонометрических уравнений
2. sint = а, где
| а |≤ 1
или
Частные случаи
1) sint=0
t =
πk‚ kЄZ2) sint=1
t = π/2+2πk‚ kЄZ
3) sint = - 1
t = - π/2+2πk‚ kЄZ
Слайд 10Формулы корней простейших тригонометрических уравнений
3. tgt = а, аЄR
t
= arctg а + πk‚ k ЄZ
4. ctgt = а,
а ЄRt = arcctg а + πk‚ kЄZ
Слайд 141.Сводимые к квадратным
Решаются методом введения новой переменной
a∙sin²x
+ b∙sinx + c=0
Пусть sinx = p, где |p| ≤1,
тогда a∙p² + b∙p + c = 0 Найти корни, вернуться к замене и решить простые уравнения.
2.Однородные
1)Первой степени:
Решаются делением на cos х (или sinx) и методом введения новой переменной.
a∙sinx + b∙cosx = 0
Т.к. sinx и cosx одновременно не равны нулю, то разделим обе части уравнения на cosx (или на sinx). Получим: простое уравнение
a∙tgx + b = 0 или tgx = m
Слайд 152) Однородные уравнения второй степени:
Решаются делением на cos² х (или
sin²x) и методом введения новой переменной.
a∙sin²x + b∙sinx∙cosx + c∙cos²x
= 0Разделим обе части на cos²x. Получим квадратное уравнение:
a∙tg²x + b∙tgx + c = 0.
3).Уравнение вида:
А sinx + B cosx = C. А, В, С 0
Слайд 16Формулы.
Универсальная
подстановка.
х + 2n;
Проверка обязательна!Понижение степени.
= (1 + cos2x ) : 2
= (1 – cos 2x) : 2
Метод вспомогательного аргумента.
Слайд 25Простые советы.
Увидел квадрат – понижай степень.
Увидел произведение – делай сумму.
Увидел сумму – делай произведение.
Слайд 261.Потеря корней:
делим на g(х).
опасные формулы (универсальная подстановка).
Этими операциями
мы сужаем область определения.
2. Лишние корни:
возводим в
четную степень.умножаем на g(х) (избавляемся от знаменателя).
Этими операциями мы расширяем область определения.
Потеря корней, лишние корни.


![Особенности решения тригонометрических уравнений Арккосинус0π1-1arccos(-а)Арккосинусом числа а называется такое число (угол) t из [0;π], чтоcos Арккосинус0π1-1arccos(-а)Арккосинусом числа а называется такое число (угол) t из [0;π], чтоcos t = а. Причём, | а](/img/thumbs/f95b9a9083d6651020d1e0c50d500a65-800x.jpg)