Плазма в електричному полі. Провідність плазми

Е (за умови В = 0) в плазмі виникає направлений

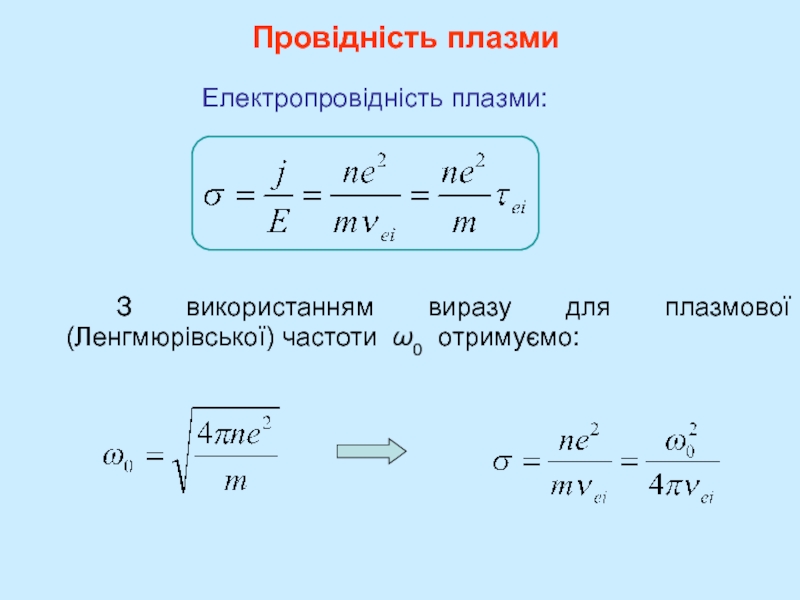
рух заряджених частинок – струм, густина якого

де ui, ue – середні швидкості руху іонів та електронів вздовж вектора .
Оскільки

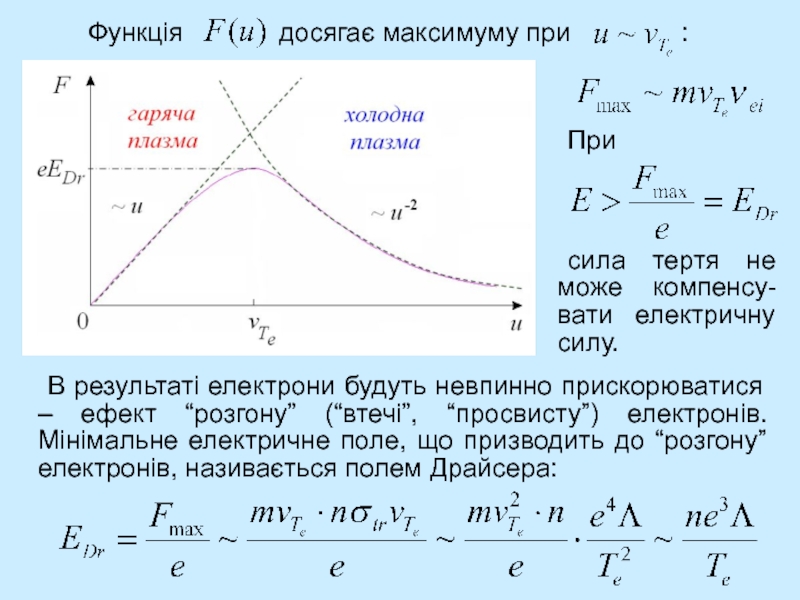
Під дією електричного поля перш за все починають прискорюватися електрони. В результаті виникає сила тертя з боку іонів, яка повинна компенсувати електричну силу:

u – середня швидкість електронів, що встановилась в результаті балансу цих сил.

плазми ( ) сила тертя

(див. попер. лекцію):

Враховуючи вирази для транспортного перерізу та частоти зіткнень

які оцінюємо для теплової швидкості електронів, отримуємо:

– середнє значення направленого імпульсу, що втрачається в кожному із зіткнень електронів з іонами (з частотою .

– випадкова складова швидкості. При усередненні за

проміжок часу, за який відбувається багато зіткнень, випадкова складова сили → 0 і залишається складова сили, що направлена проти швидкості .

2) Для холодної плазми ( ) частота зіткнень буде визначатися швидкістю направленого руху . В цьому випадку середня сила тертя (див. попер. лекцію):

Таким чином,

– гаряча плазма

– холодна плазма

:
При
В результаті

електрони будуть невпинно прискорюватися – ефект “розгону” (“втечі”, “просвисту”) електронів. Мінімальне електричне поле, що призводить до “розгону” електронів, називається полем Драйсера:

сила тертя не може компенсу-вати електричну силу.

для “розгону” основної групи електронів, що мають швидкість порядка теплової.

Але й при

плазма містить електрони із швидкістю, що значно перевищує теплову швидкість (т.з. максвелівський хвіст). Сила тертя на ці електрони мала і вони будуть прискорюватися навіть в полі, меншому за .

з іонами, пропорційна , і, відповідно росте ~

. При достатньо великій швидкості теплового руху направлена швидкість може досягнути величини того ж порядку, що й , чи навіть її перевищити. В такій ситуації спрощена модель, згідно з якою електрон набирає на довжині пробігу невелику направлену швидкість і повністю її втрачає при сильному зіткненні, непридатна.
В дійсності прискорення і гальмування електрона відбувається одночасно. Поки електрон набирає швидкість, резерфордівське розсіяння на іонах поступово змінює напрямок його руху. Електричне поле намагається випрямити траєкторію руху, в той час як взаємодія з іонами її згинає. Якщо приріст направленої компоненти швидкості не компенсується розсіянням, то рівновага сил не може встановитися і електрон переходить в процес безперервного прискорення.

“розгону” буде прискорюватися до тих пір, поки він знаходиться в

цьому полі.
В стан “розгону” полем переходять ті електрони, які встигають набрати на довжині вільного пробігу λ додаткову направлену швидкість u, що перевищує їх початкову швидкість vT.

Умова “розгону”:

Для водневої плазми:

Така умова задовольняється для електронів з We >> Te.

= 0.
Малое внешнее поле Е ускоряет электроны до тех

пор, пока сила трения об ионы не уравновесит электрическую силу.

З балансу електричної сили і сили тертя

частоти ω0 отримуємо:

плазми швидко зростає при збільшенні температури і практично не залежить

(слабка залежність через Λ) від густини n.

Λ ≈ 15 :

Для багатокомпонентної
плазми (Z1,

… , Zn):

де αk – парціальні концентрації іонів із зарядом Zk. Наявність багатозарядних іонів значно знижує провідність плазми.

– n = 1010 см-3
3 – n = 1015

см-3

Питомий опір, метали [ом·м]:
Мідь 1,7 · 10-8
Нержавіюча сталь 7,0 · 10-7
Ртуть 1,0 · 10-6

Питомий опір, плазма:

значення має механічна інерція електронів. Нехай напруженість поля:
а х

– зміщення електрона вздовж вектора .
Рівняння руху :

Розв’язок:

випадку постійного електричного поля (ω = 0) маємо раніше отриманий

вираз (слайд 9):

знехтувати. При νei

уявною:

Струм запізнюється по фазі відносно напруженості на 90º – інерція електронів.