Последовательности. Предел последовательности

…,  n – 1,  n, п + 1, …
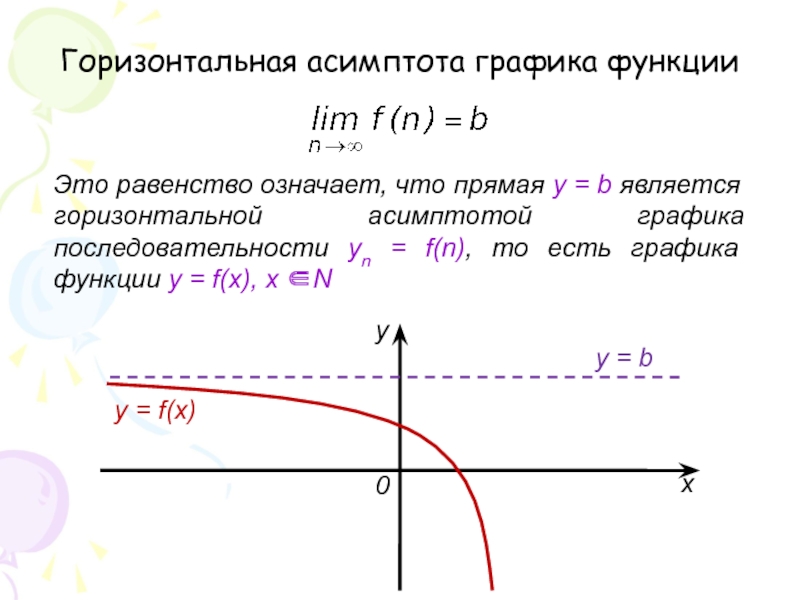
Функцию y

Обычно числовая последовательность задаётся некоторой формулой уn = f(n), позволяющей найти любой член последовательности по его номеру n;
эта формула называется формулой общего члена.

чисел;
2,  4,  6,  8,  10, … – ряд чётных чисел;
1,

Последовательность простых чисел:
2; 3; 5; 7; 11; 13; 17;

члены не больше некоторого числа.

Пример: -1, -4, -9, -16, …, -п2, … - ограничена сверху 0.

Последовательность {уn} ограниченна сверху, если существует число M такое, что для любого п выполняется неравенство
уп ≤ М
Число М называют верхней границей последовательности.

члены не меньше некоторого числа.

Пример: 1, 4, 9, 16, …, п2, … - ограничена снизу 1.

Последовательность {уn} ограниченна снизу, если существует число m такое, что для любого п выполняется неравенство
уп ≥ m
Число m называют нижней границей последовательности.

Если последовательность ограничена и сверху и снизу, то ее называют ограниченной последовательностью.

каждый ее член больше предыдущего:
у1 < y2 < y3

Пример: 1, 3, 5, 7, 9, 2п – 1, … - возрастающая последовательность.

Последовательность {уn} называют убывающей последовательностью, если каждый ее член меньше предыдущего:
у1 > y2 > y3 > y4 > … > yn > yn+1 > …

Пример: 1, 1/3, 1/5, 1/7, 1/(2п – 1), … - убывающая последовательность.

Возрастающие и убывающие последовательности называют монотонными

к некоторому числу a при увеличении порядкового номера n.
В

Число а называется пределом числовой последовательности {un}
если для любого ε > 0 найдется такое число N = N(ε), зависящее от ε, что │un – a│< ε при n > N

если её общий член неограниченно приближается к a  при возрастании 

Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.

то последовательность уn = q n расходится
Если mN, kR,

суммы равен сумме пределов:

постоянный множитель можно вынести за знак предела:

асимптотой графика последовательности yn = f(n), то есть графика функции

Горизонтальная асимптота графика функции

х

у

y = f(x)

0

у = b

b является горизонтальной асимптотой графика функции y = f(x).
х
у
y =

0

у = b

Будем говорить, что функция f(x) стремится к пределу b при x → ∞, если для произвольного малого положительного числа ε можно указать такое положительное число M, что для всех значений x, удовлетворяющих неравенству |x| > M, выполняется неравенство |f(x) − b| < ε.

b при x → a, если для каждого положительного числа

х

y = f(x)

0

b

у

а

x  a (или при x 

ПРИМЕР: Функция является бесконечно малой при x  3.
В других точках эта функция бесконечно малой не является!

Теорема. Если функция f (x) при x  a имеет предел, равный А, то ее можно представить в виде суммы предела A и бесконечно малой  (x) при x  a:

Свойства бесконечно малых

Теорема 1. Сумма двух бесконечно малых есть бесконечно малая величина.

Теорема 2. Произведение бесконечно малой на ограниченную функцию (в том числе на постоянную, на другую бесконечно малую функцию) есть бесконечно малая.

 a (или при x  ), если для любого,

Теорема 1. Если  (x) – бесконечно малая, то 1/(x) бесконечно большая.

Теорема 2. Если  (x) – бесконечно большая, то 1/(x) бесконечно малая.

Связь между б.м. и б.б.

называют эквивалентными при x  a (или при x 

функций равен сумме (разности) пределов:
Предел произведения двух функций равен произведению

Постоянный множитель можно выносить за знак предела:

предел знаменателя не равен нулю:
Предел степени с натуральным показателем равен

Предел показательно – степенной функции:

монотонна и ограничена при x < x0 или при
x

или ее правый предел:

f(x).
Если при этом получается конечное число, то предел равен этому

Если при подстановки предельного значения x0 в функцию f(x) получаются выражения вида:

то предел будет равен:

получаются выражения следующих видов:
Эти выражения называются неопределенности, а вычисление пределов

малая того же порядка, что и сам угол.

последовательности:



Это пример последовательности, которая монотонная и ограничена.