Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхности вращения
Содержание
- 1. Поверхности вращения
- 2. Поверхность α , образованная вращением образующей ℓ вокруг неподвижной оси i, называется поверхностью вращения
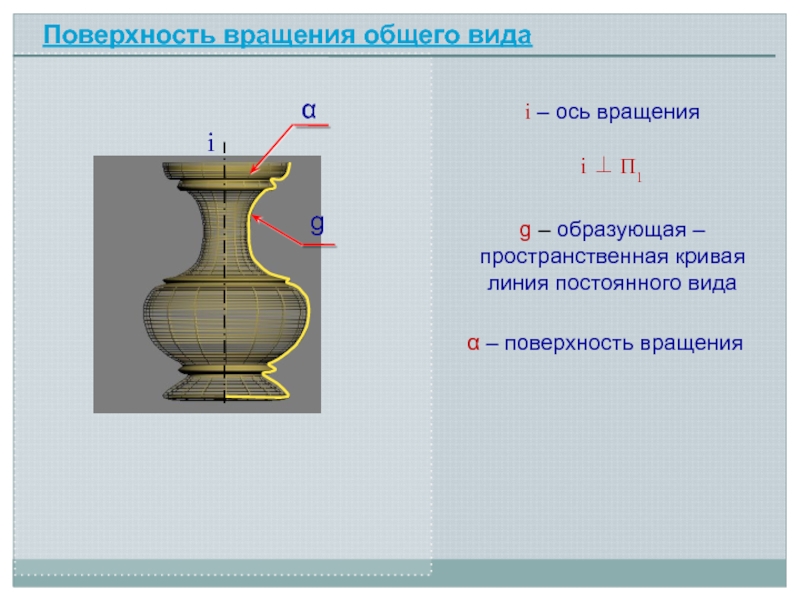
- 3. i – ось вращенияПоверхность вращения общего видаig
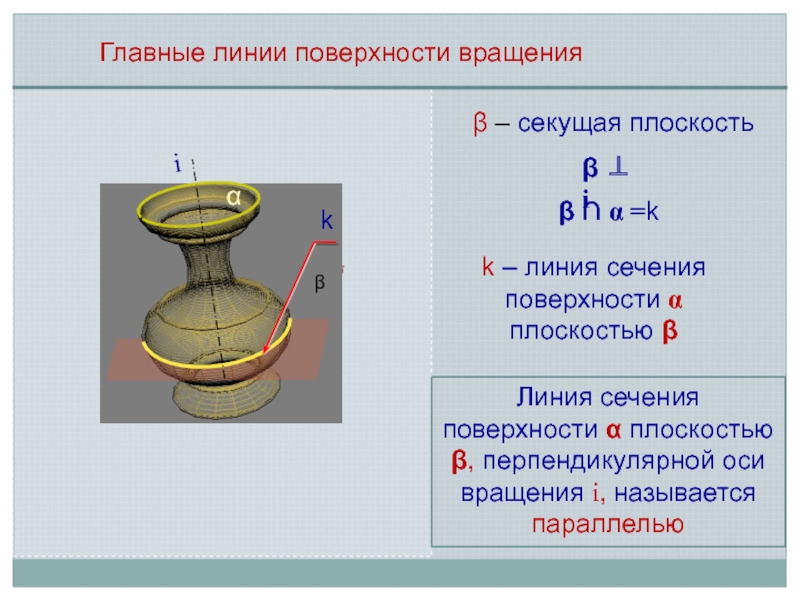
- 4. – секущая плоскостьГлавные линии поверхности вращенияk
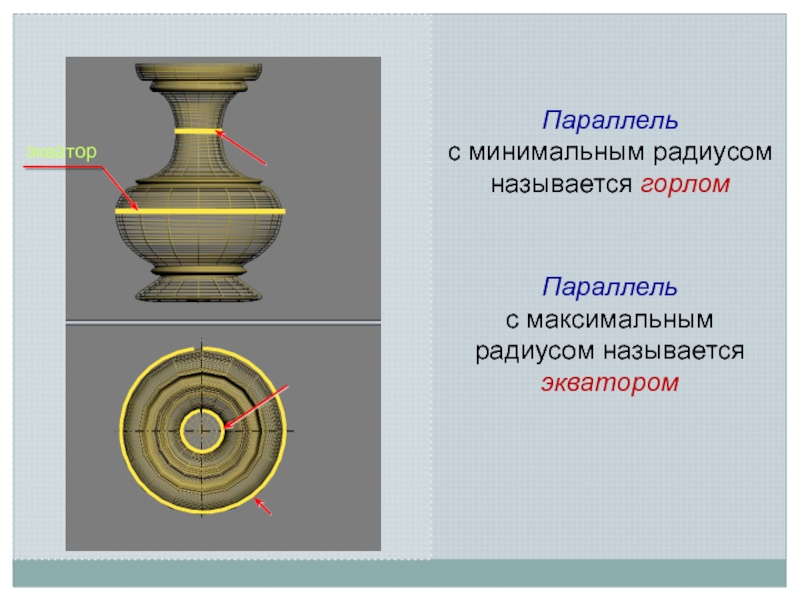
- 5. горлогорлоэкваторПараллель с минимальным радиусом называется горломПараллель с максимальным радиусом называется экваторомэкватор
- 6. iλλ – секущая плоскостьm – линия сечения
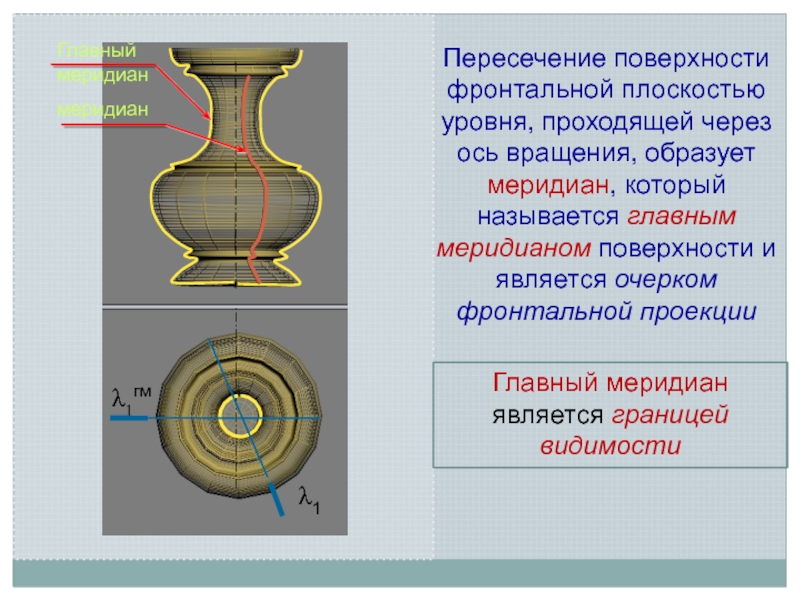
- 7. Главный меридианмеридианλ1гмПересечение поверхности фронтальной плоскостью уровня, проходящей
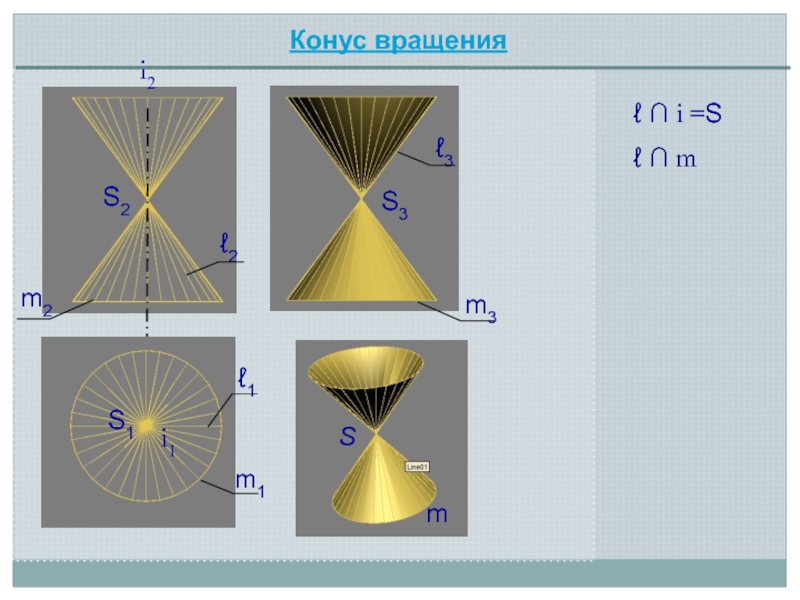
- 8. i2S2Sℓ i =Sℓ2S1S3i1ℓ1m1m2ℓ mm3mℓ3Конус вращения
- 9. Принадлежность точки поверхности
- 10. Точка принадлежит поверхности, если она принадлежит линии,
- 11. Среди точек кривой выделяют опорные точки:– экстремальные
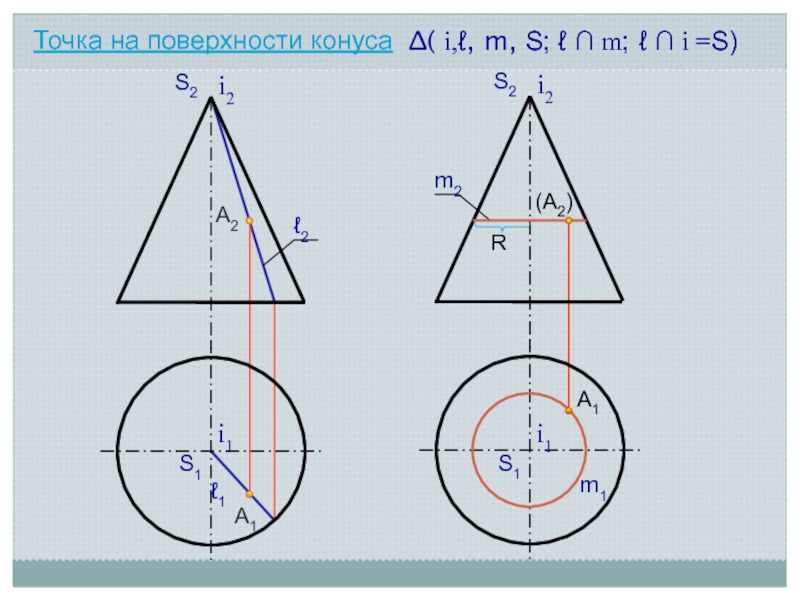
- 12. А2А1i2S2∆( i,ℓ, m, S; ℓ m; ℓ i =S)ℓ2S1i1ℓ1(А2)А1i2S2m2S1i1m1Точка на поверхности конусаR
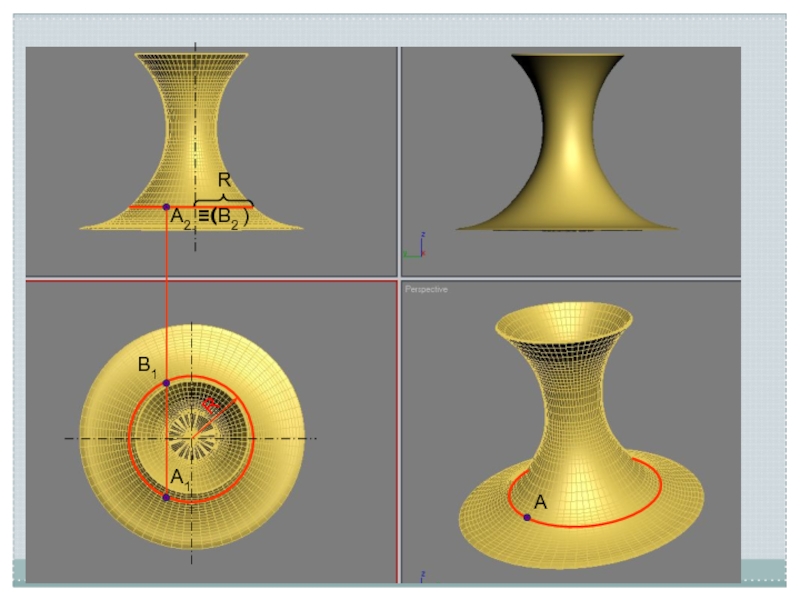
- 13. Вогнутый тор (глобоид)Поверхность, образованная внутренней стороной вращающейся дуги радиусом R, называется глобоидом
- 14. RRА2 (В2 ) А1АВ1
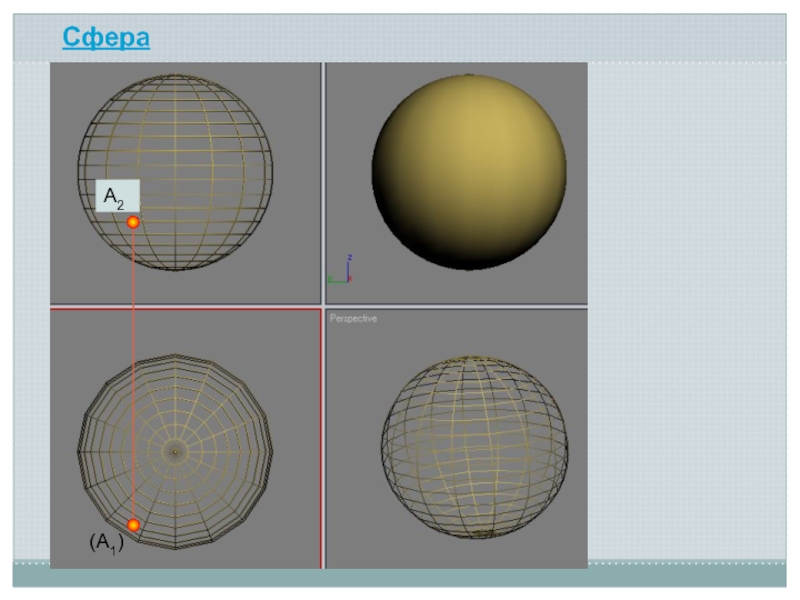
- 15. A2(A1)Сфера
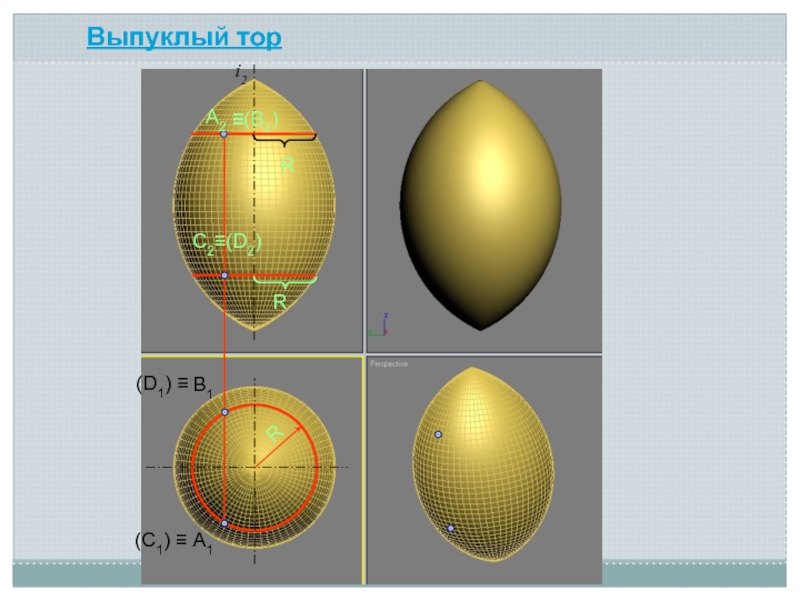
- 16. Выпуклый торRRА2А1RВ1С2(D2)(C1) (D1) (В2)i2
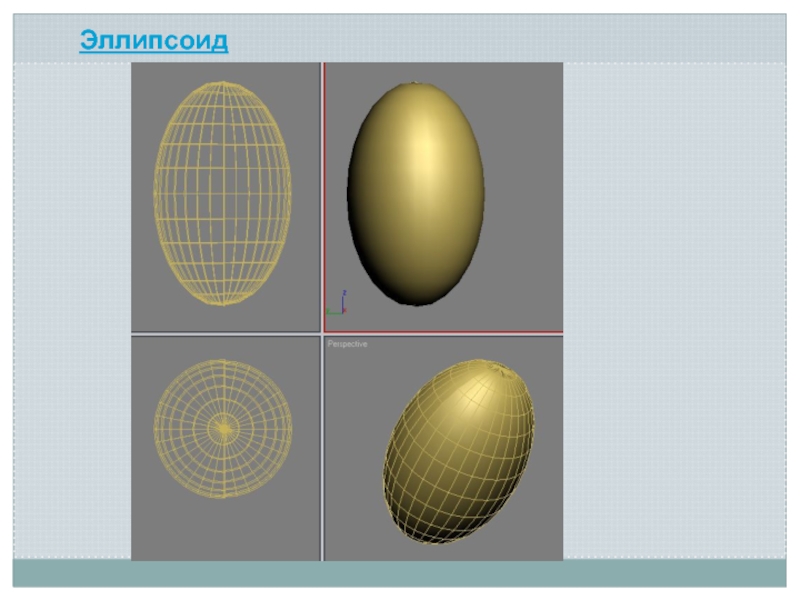
- 17. Эллипсоид
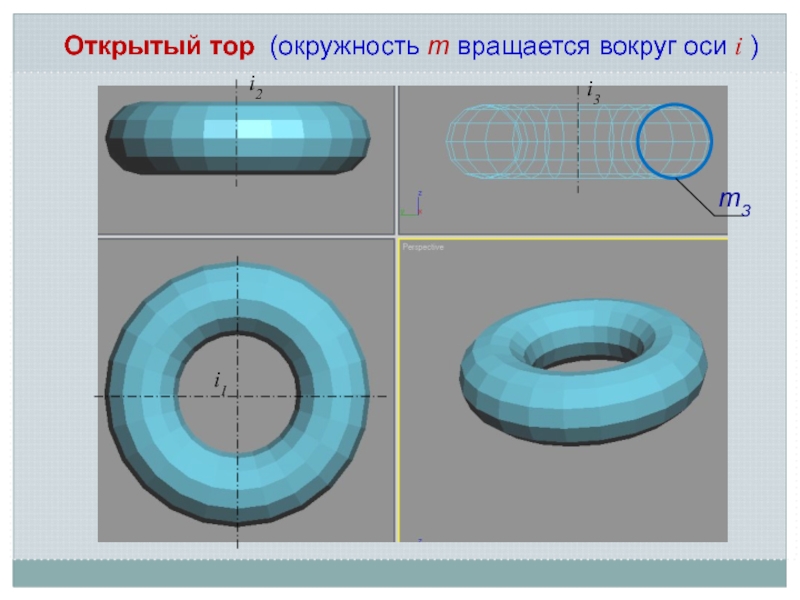
- 18. Открытый тор (окружность m вращается вокруг оси i )i2i1i3m3
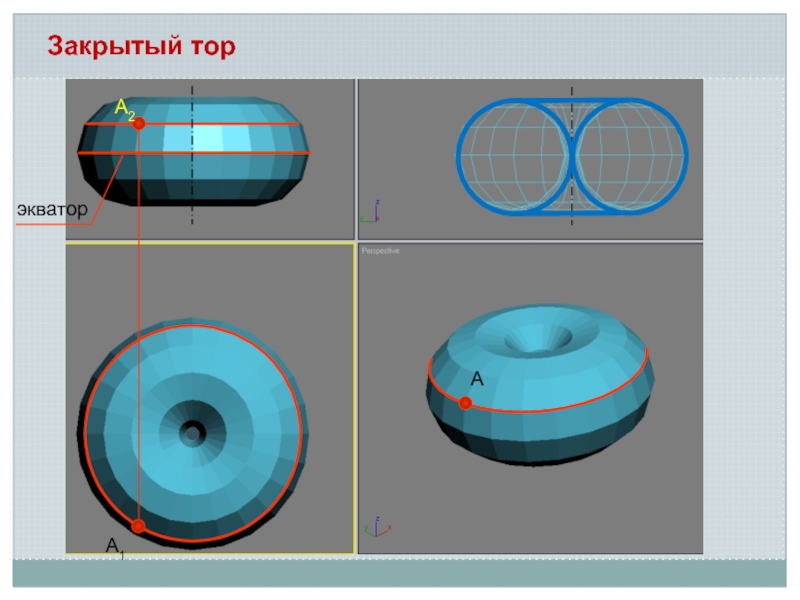
- 19. Закрытый торА2А1Аэкватор
- 20. Закрытый кольцевой тор (самопересекающийся)
- 21. Слайд 21
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Поверхность α , образованная вращением образующей ℓ вокруг неподвижной оси
i, называется поверхностью вращения
Слайд 3i – ось вращения
Поверхность вращения общего вида
i
g – образующая –
пространственная кривая линия постоянного вида
g
– поверхность вращения
i
П1 Слайд 4 – секущая плоскость
Главные линии поверхности вращения
k – линия сечения
поверхности плоскостью
k
i
i
Линия сечения поверхности плоскостью
, перпендикулярной оси вращения i, называется параллелью
=k
Слайд 5горло
горло
экватор
Параллель
с минимальным радиусом называется горлом
Параллель
с максимальным радиусом называется
экватором
экватор
Слайд 6i
λ
λ – секущая плоскость
m – линия сечения поверхности плоскостью
λ
λ ∈ i
Линия сечения поверхности плоскостью λ, проходящей через
ось вращения i, называется меридианом (случайным меридианом)
λ =m
m
Слайд 7Главный меридиан
меридиан
λ1гм
Пересечение поверхности фронтальной плоскостью уровня, проходящей через ось вращения,
образует меридиан, который называется главным меридианом поверхности и является очерком
фронтальной проекцииГлавный меридиан является границей видимости
λ1
Слайд 10Точка принадлежит поверхности, если она принадлежит линии, расположенной на этой
поверхности
Линия принадлежит поверхности, если каждая ее точка принадлежит этой поверхности
Слайд 11Среди точек кривой выделяют опорные точки:
– экстремальные точки – высшая
и низшая, крайняя левая и крайняя правая, самая далекая и
самая ближняя точки кривой;– граничные точки видимости кривой, принадлежащей поверхности, лежат на очерках поверхности и отделяют видимую часть поверхности от ее невидимой части