Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллельные прямые в пространстве
Содержание
- 1. Параллельные прямые в пространстве
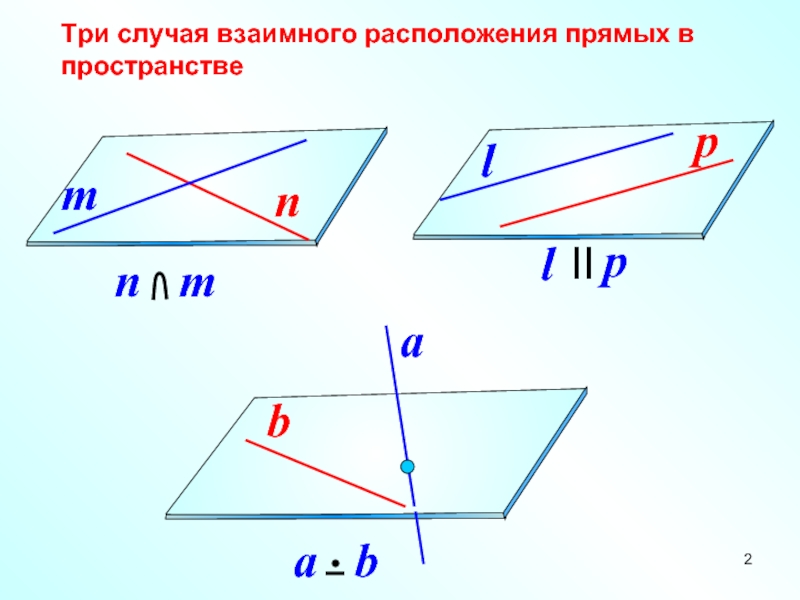
- 2. Три случая взаимного расположения прямых в пространстве
- 3. ПланиметрияСтереометрияДве прямые на плоскости называются параллельными, если
- 4. Две прямые в пространстве называются параллельными, если
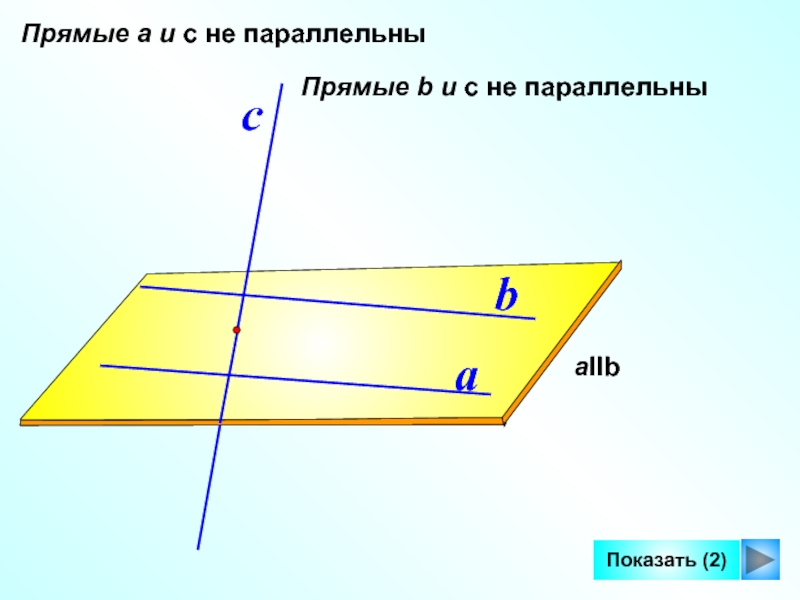
- 5. abaIIbсПрямые а и с не параллельныПоказать (2)Прямые b и с не параллельны
- 6. Две параллельные прямые определяют плоскость.(определение параллельных прямых)abПоказать (1)
- 7. Два отрезка называются параллельными, если они лежат
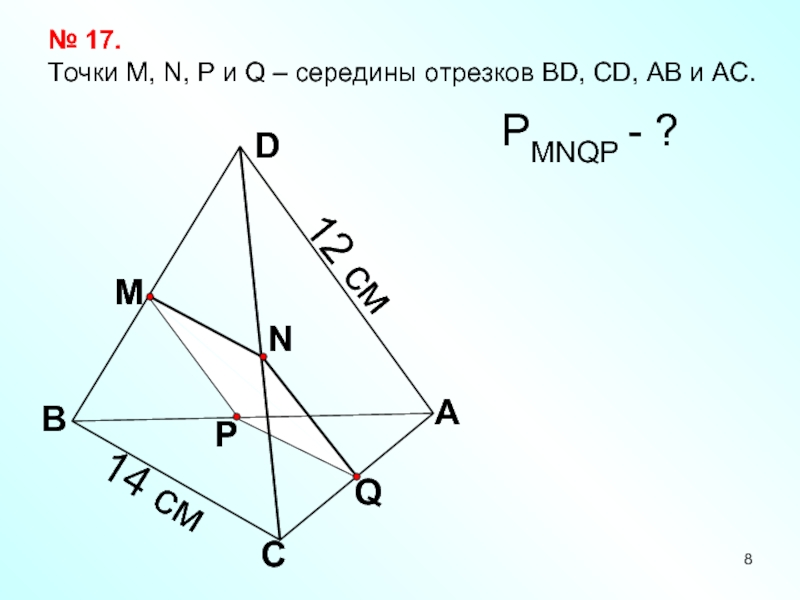
- 8. QАСВDNMP№ 17. Точки М, N, P и
- 9. А Через точку, не лежащую
- 10. ТеоремаЧерез любую точку пространства,
- 11. Повторим. Следствие из аксиомы
- 12. Лемма
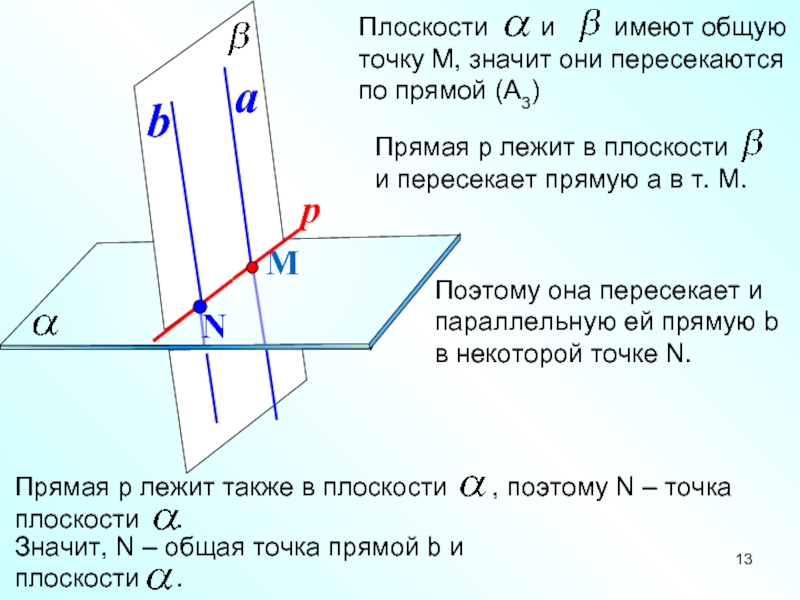
- 13. МaПоэтому она пересекает и параллельную ей прямую b в некоторой точке N.
- 14. Проверить (3)№ 19. Прямые, содержащие стороны АВ
- 15. Повторим. Следствие из аксиомы
- 16. abс ТеоремаЕсли две прямые параллельны
- 17. Дано: АА1 II
- 18. Дано: А1С1 = АС,
- 19. АВСЕFKM Треугольник АВС и
- 20. АВССDKM Квадрат АВСD и трапеция KMNL не
- 21. Отрезок АВ не
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3
Планиметрия
Стереометрия
Две прямые на плоскости называются параллельными, если они не пересекаются.
Две
прямые в пространстве называются параллельными, если они лежат в одной
плоскости и не пересекаются.aIIb
aIIb
Слайд 4Две прямые в пространстве называются параллельными, если
1) они лежат
в одной плоскости и
2) не пересекаются
a
b
Определение
Показать (1)
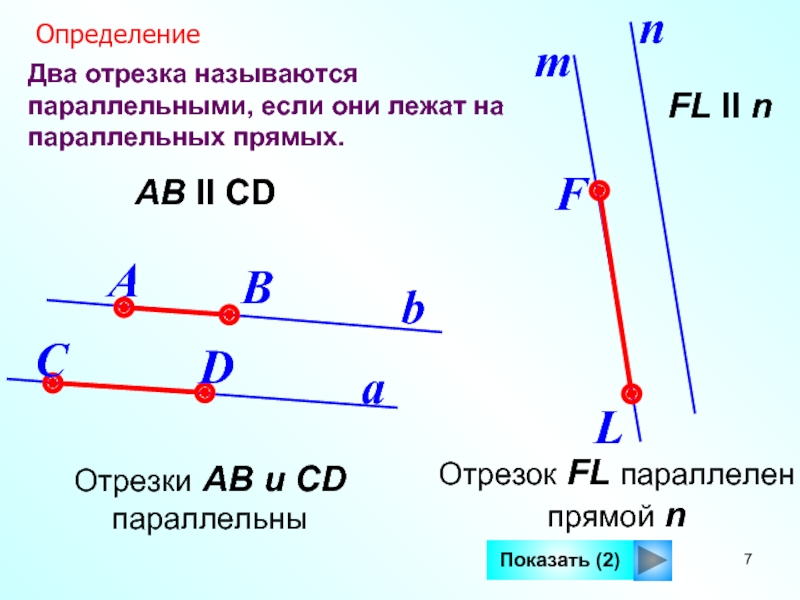
Слайд 7Два отрезка называются параллельными, если они лежат на параллельных прямых.
a
b
Определение
АВ II СD
FL II n
Показать (2)
Отрезок FL параллелен
прямой
nОтрезки АВ и СD параллельны
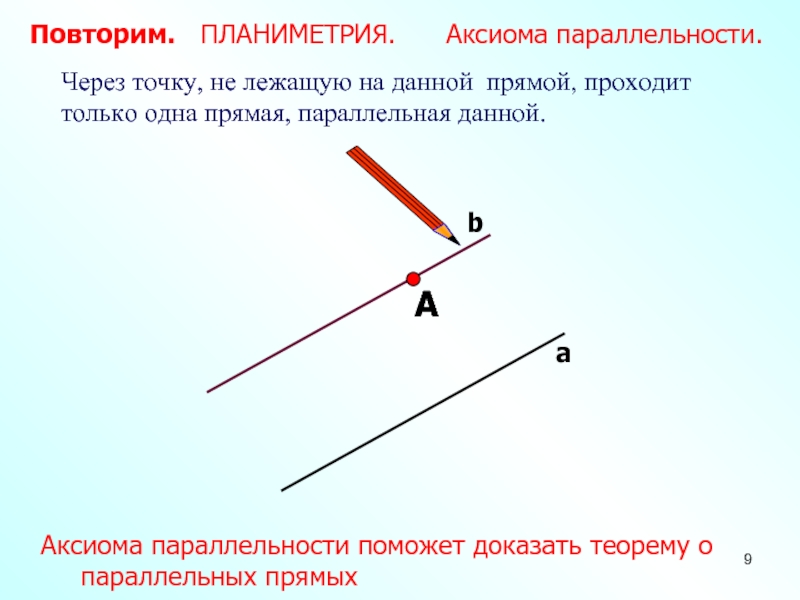
Слайд 9А
Через точку, не лежащую на данной прямой,
проходит только одна прямая, параллельная данной.
Повторим. ПЛАНИМЕТРИЯ.
Аксиома параллельности. а
b
Аксиома параллельности поможет доказать теорему о параллельных прямых
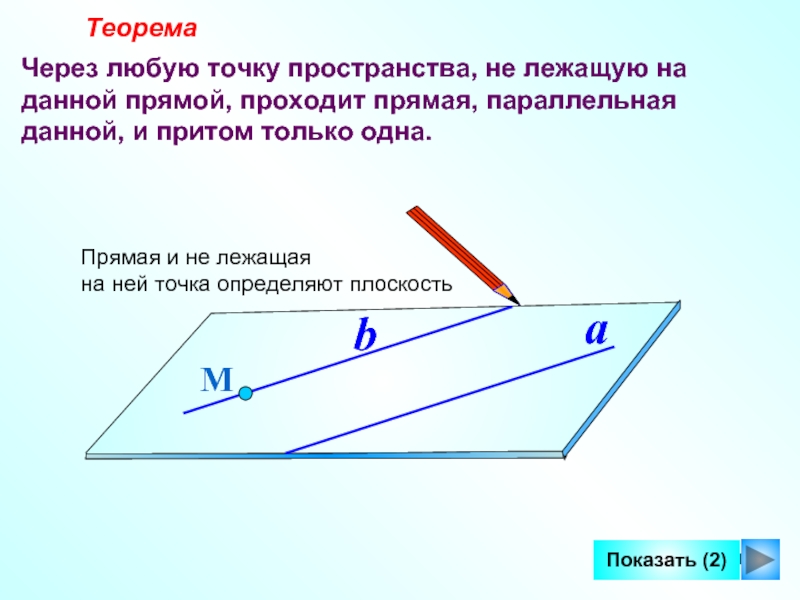
Слайд 10 Теорема
Через любую точку пространства, не лежащую на
данной прямой, проходит прямая, параллельная данной, и притом только одна.
М
a
b
Прямая
и не лежащая на ней точка определяют плоскость
Показать (2)
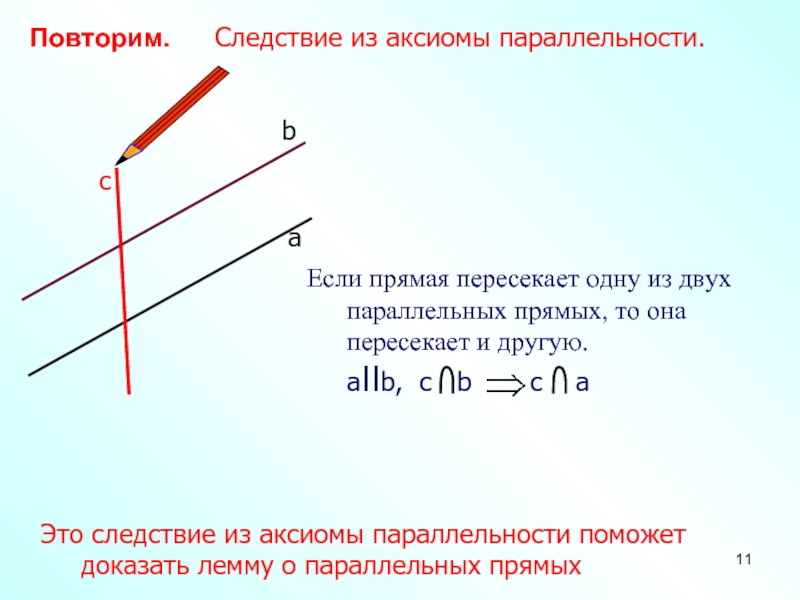
Слайд 11Повторим. Следствие из аксиомы параллельности.
а
c
b
Это следствие
из аксиомы параллельности поможет доказать лемму о параллельных прямых
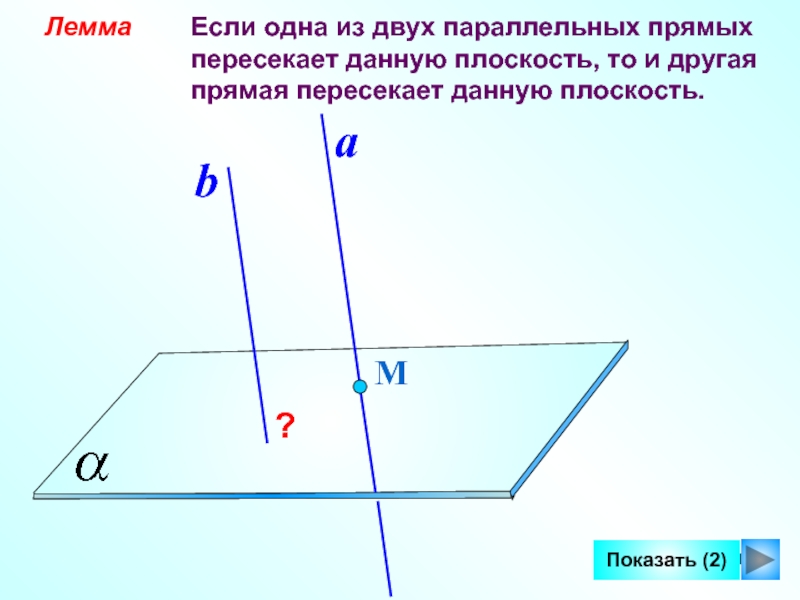
Слайд 12 Лемма
Если одна из двух параллельных
прямыхпересекает данную плоскость, то и другая
прямая пересекает данную плоскость.
М
Показать (2)
a
?
Слайд 14
Проверить (3)
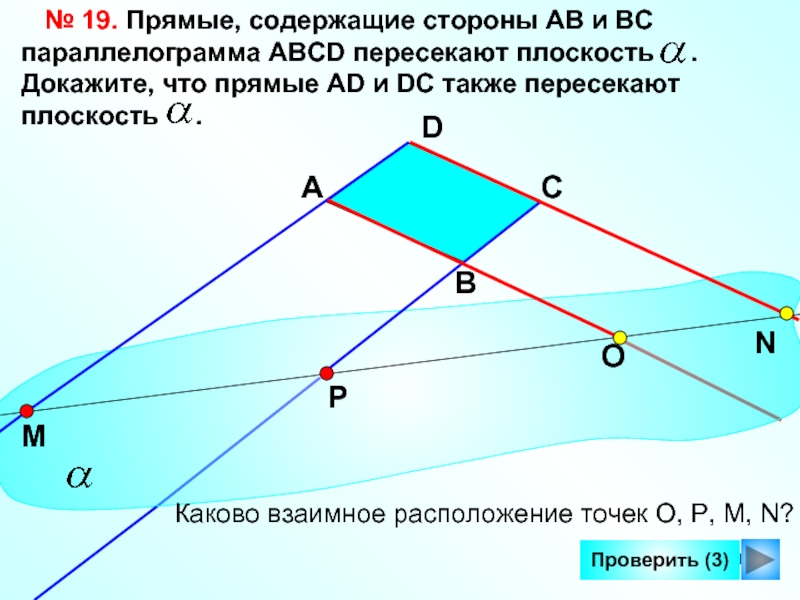
№ 19. Прямые, содержащие стороны АВ и ВС параллелограмма
AВСD пересекают плоскость . Докажите, что прямые AD
и DC также пересекают плоскость .С
А
О
D
Каково взаимное расположение точек О, Р, М, N?
Р
М
N
В
Слайд 15Повторим. Следствие из аксиомы параллельности.
Аналогичное утверждение
имеет место и для трех прямых в пространстве.
Слайд 16
a
b
с
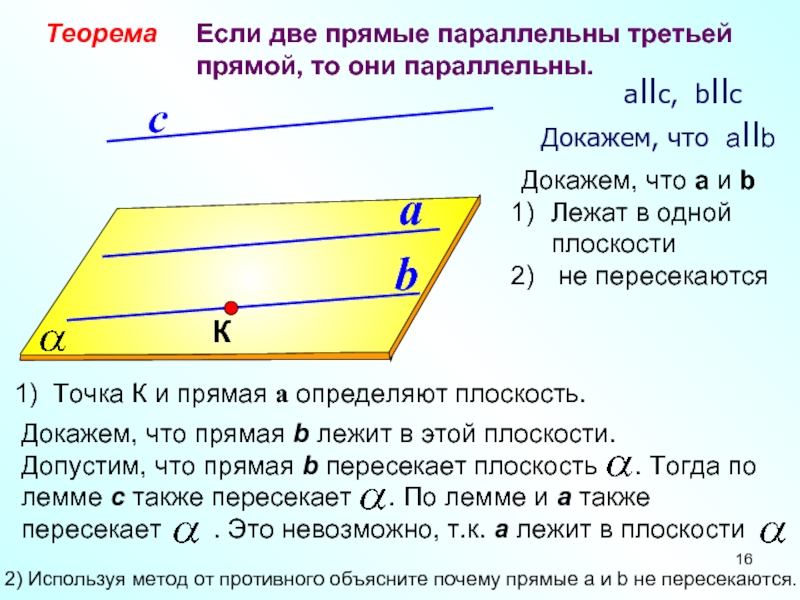
Теорема
Если две прямые параллельны третьей прямой, то
они параллельны.
aIIс, bIIс
Докажем, что
aIIb1) Точка К и прямая а определяют плоскость.
Докажем, что а и b
Лежат в одной плоскости
не пересекаются
2) Используя метод от противного объясните почему прямые а и b не пересекаются.
Слайд 19
А
В
С
Е
F
K
M
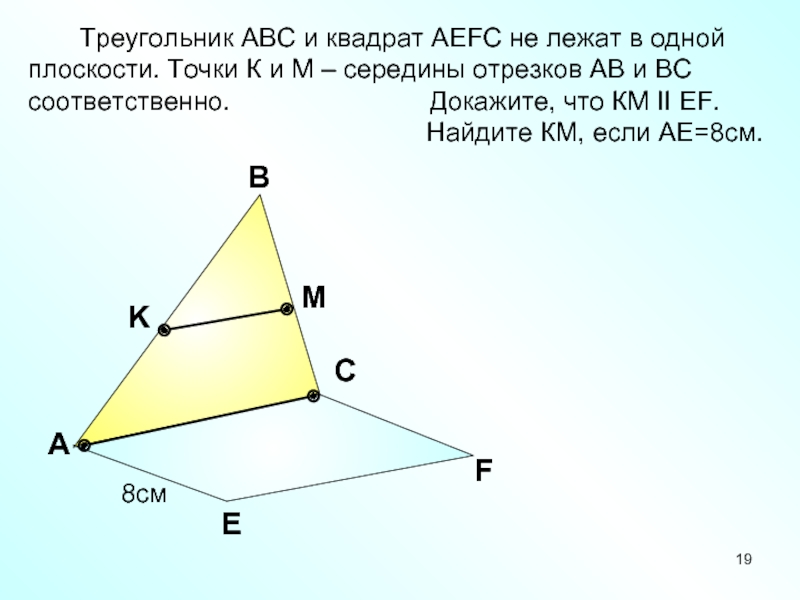
Треугольник АВС и квадрат АEFC не
лежат в одной
плоскости. Точки К и М – середины
отрезков АВ и ВС соответственно. Докажите, что КМ II EF.Найдите КМ, если АЕ=8см.
8см
Слайд 20
А
В
С
С
D
K
M
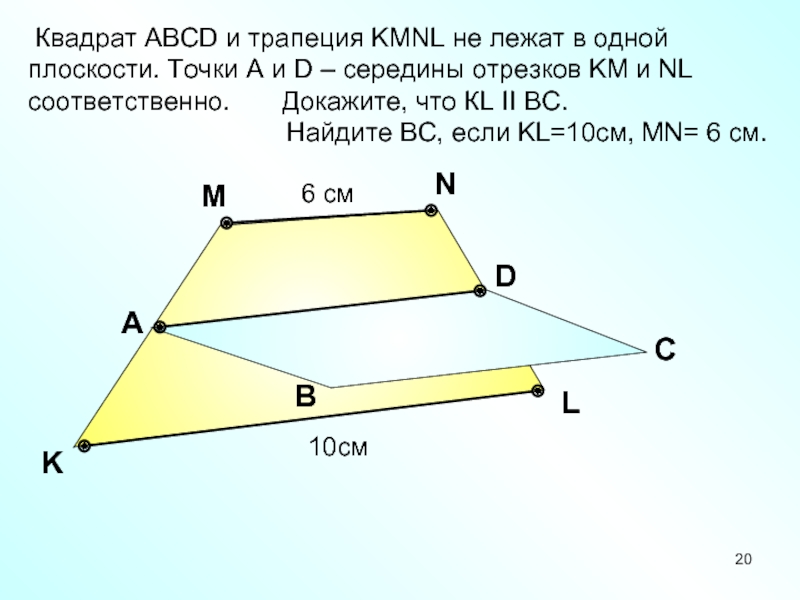
Квадрат АВСD и трапеция KMNL не лежат в одной
плоскости. Точки A и D – середины отрезков KM и
NL соответственно. Докажите, что КL II BC.Найдите BC, если KL=10см, MN= 6 см.
N
L
10см
6 см
Слайд 21
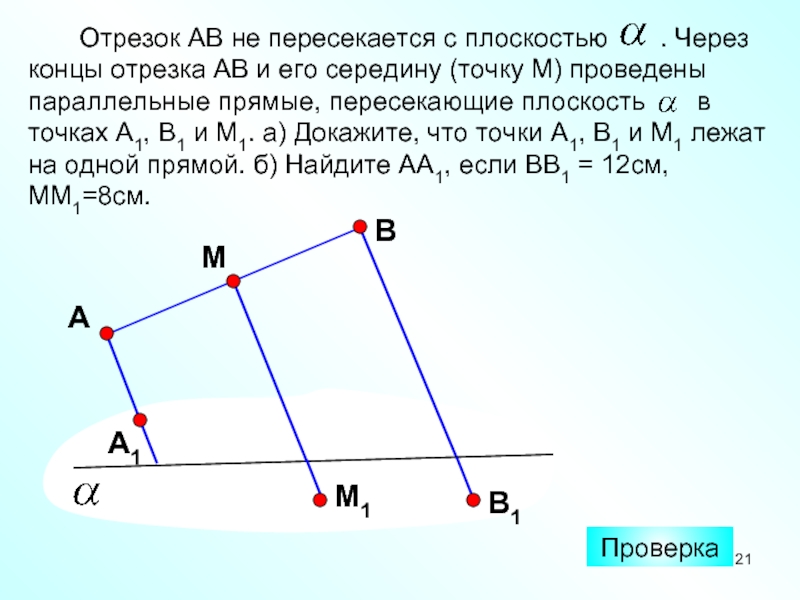
Отрезок АВ не пересекается с плоскостью
. Через концы отрезка АВ и его
середину (точку М) проведены параллельные прямые, пересекающие плоскость в точках А1, В1 и М1. а) Докажите, что точки А1, В1 и М1 лежат на одной прямой. б) Найдите АА1, если ВВ1 = 12см, ММ1=8см.А
М
В
Проверка