Применение производной для исследования функции на монотонность и экстремумы

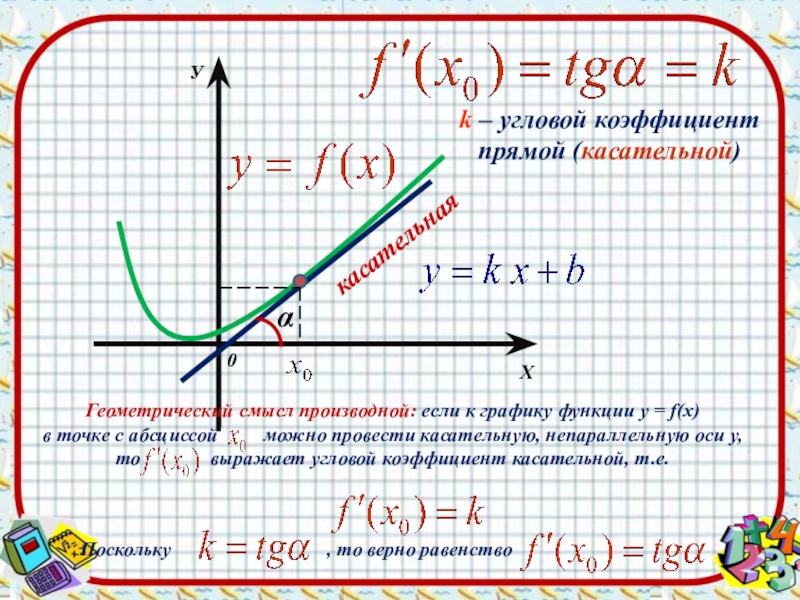
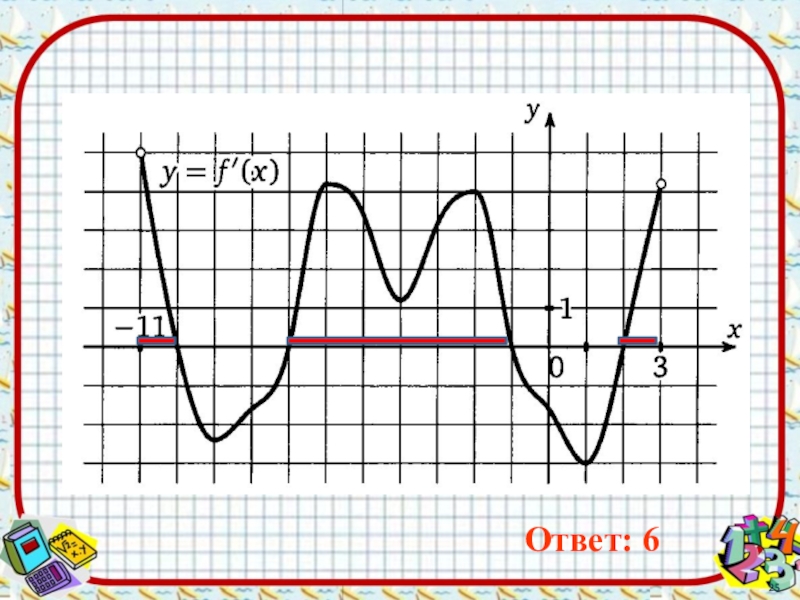
графику функции y = f(x)
в точке с абсциссой

можно провести касательную, непараллельную оси у,
то выражает угловой коэффициент касательной, т.е.

Поскольку , то верно равенство

90°, то k < 0.
Если α = 0°, то k

= 0.
Касательная параллельна оси ОХ.

0

неравенство f!(х)≥0 (причем равенство f!(х)=0 выполняется лишь в изолированных точках),

то функция у= f(х) возрастает на промежутке Х.
Теорема 2. Если во всех точках открытого промежутка Х выполняется неравенство f!(х)≤0 (причем равенство f!(х)=0 выполняется лишь в изолированных точках), то функция у= f(х) убывает на промежутке Х.
Теорема 3. Если во всех точках открытого промежутка Х выполняется равенство f!(х)=0,то функция у= f(х) постоянна на промежутке Х.

монотонность – это значит выяснить, на каких промежутках области определения

функция возрастает, а на каких – убывает. Согласно теоремам 1 и 2, это связано со знаком производной.
Найдем производную данной функции:

и в его концевых точках (именно так обстоит дело для

заданной функции), эти концевые точки включают в промежуток монотонности функции.

-1

0

+

х

+

f!(х)

f(х)

Ответ: функция возрастает хЄ(-∞; - 1], [0;+∞), функция убывает хЄ[-1 ; 0]

0
На графике две уникальные точки: (-1;0) и (0;-1). В этих

точках:
1) происходит изменение характера монотонности функции;
2) касательная к графику функции параллельна оси Х (или совпадает с осью Х), т.е. производная функции в каждой из указанных точек равна нулю;
f(-1) – наибольшее значение функции, но не во всей области определения, а по сравнению со значениями функции из некоторой окрестности точки х = - 1. Также f(0) – наименьшее значение функции в окрестности точки х=0

f(х), если у этой точки существует окрестность, для всех точек

которой (кроме самой точки х=х0) выполняется неравенство
f(х)>f(х0).

Определение 2. Точку х=х0 называют точкой максимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой (кроме самой точки х=х0) выполняется неравенство
f(х)

путать с наибольшим (или наименьшим) значением функции во всей рассматриваемой

области определения, эти значения в окрестности некоторой точки Х, являются наибольшими (или наименьшими).

Точки минимума и максимума функции называют – точки экстремума (от латинского слова extremum – «крайний»)

точке х=х0, то этой точке производная либо равна нулю, либо

не существует.

Внутренние точки области определения функции, в которых производная функции равна нулю, называют стационарными, а внутренние точки области определения функции, в которых функция непрерывна, но производная не существует – критическими.

непрерывна на промежутке Х и имеет внутри промежутка стационарную или

критическую точку х=х0.Тогда:
1) Если у этой точки существует такая окрестность, в которой при х<х0, выполняется неравенство f1(x)<0, при х>х0 – неравенство f1(x)>0, то х=х0 – точка минимума функции у=f(x);
2) Если у этой точки существует такая окрестность, в которой при х<х0 выполняется неравенство f1(x) >0, а при х>х0 – неравенство f1(x)<0, то х=х0 – точка максимума функции у=f(x);
3) Если у этой точки существует такая окрестность, что в ней и слева и справа от точки х0 знаки производной одинаковы, то в точке х0 экстремума нет.

11.
Решение: найдем производную данной функции: у1=12х3 – 48х2 + 48х.

Найдем стационарные точки:

12х3 – 48х2 + 48х=0

12х(х2 – 4х + 4)=0

Производная обращается в нуль в точках х=0 и х=2

12х(х – 2)2=0

-

+

+

0

2

х

Значит, х=0 – точка минимума.

Ответ: уmin= - 11.

f1(х).
Найти стационарные (f1(х)=0) и критические (f1(х) не существует) точки функции

у=f(х).
Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
На основании теорем 1, 2, и 5 сделать выводы о монотонности функции и о ее точках экстремума.

- 8; 3). Определить количество целых точек, в которых производная

функции отрицательна

( - 7; 5). Найти точку экстремума функции на отрезке

[-6; 4]

( - 3; 8). Найти количество точек максимума функции на

отрезке [- 2; 7]

( - 3; 8). Найти промежутки убывания функции. В ответе

указать сумму целых точек, входящих в эти промежутки

( - 11; 3). Найти промежутки возрастания функции. В ответе

указать длину наибольшего из них

30.26