Прямоугольный параллелепипед

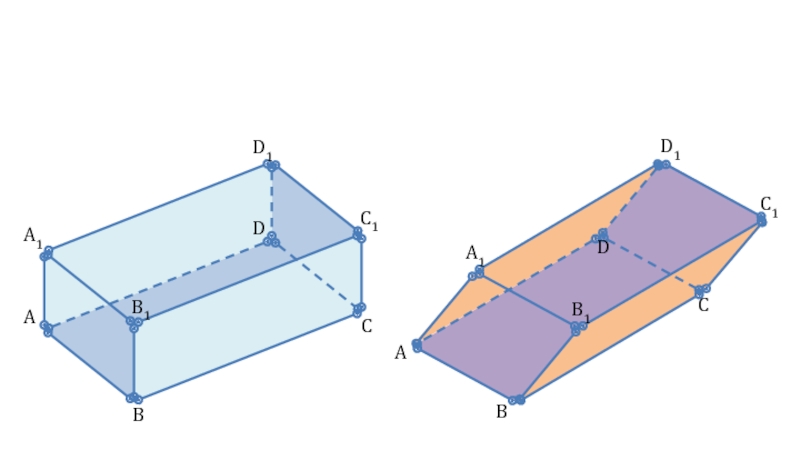
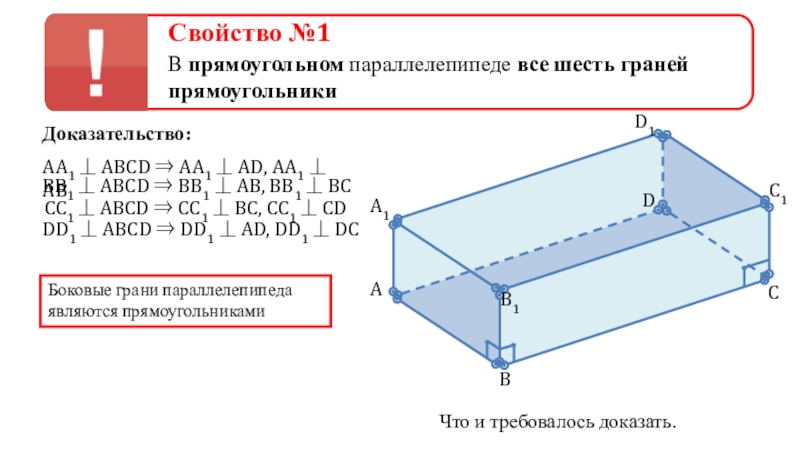
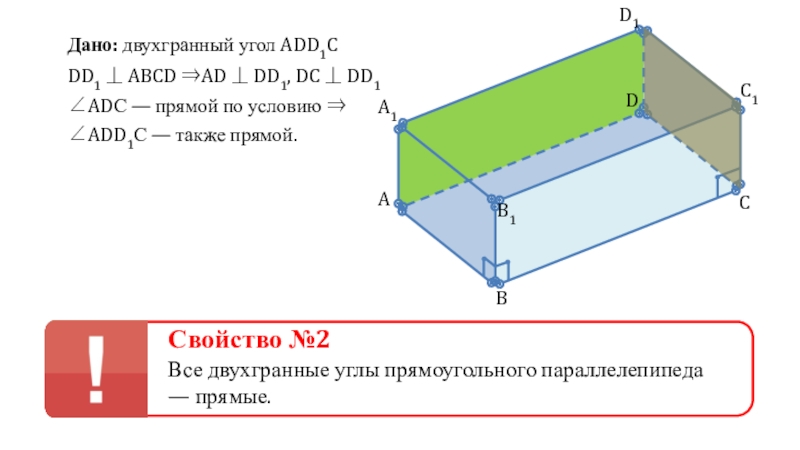
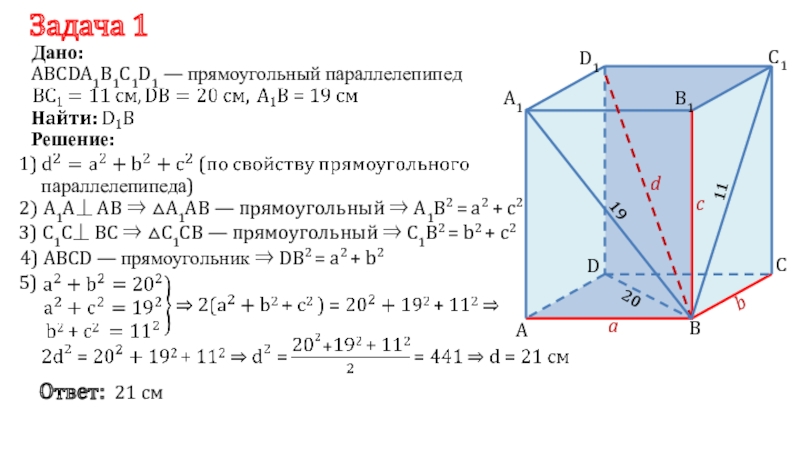
⇒ AA1 ⏊ AD, AA1 ⏊ AB

BB1 ⏊ ABCD
CC1 ⏊

DD1 ⏊ ABCD ⇒ DD1 ⏊ AD, DD1 ⏊ DC

⇒ BB1 ⏊ AB, BB1 ⏊ BC

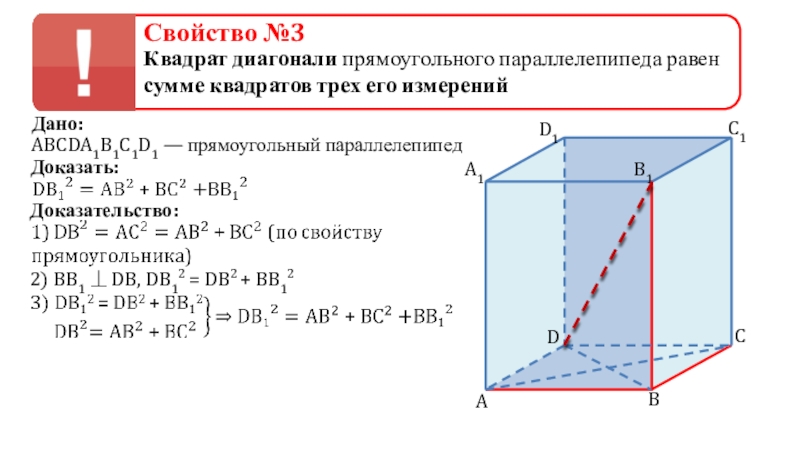
Что и требовалось доказать.

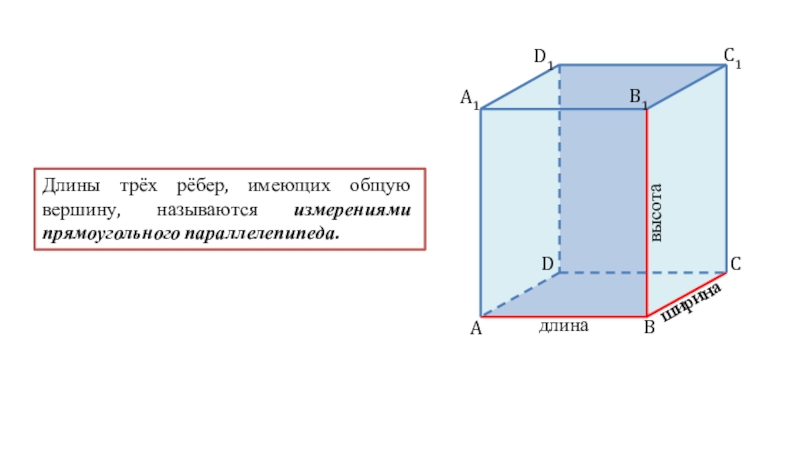
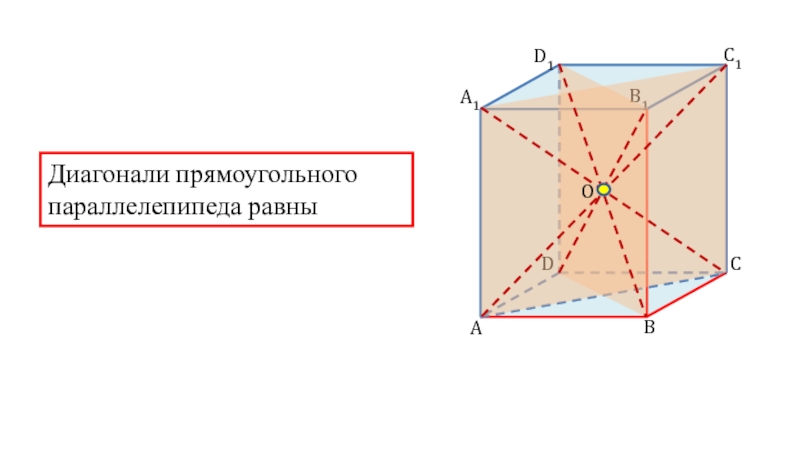
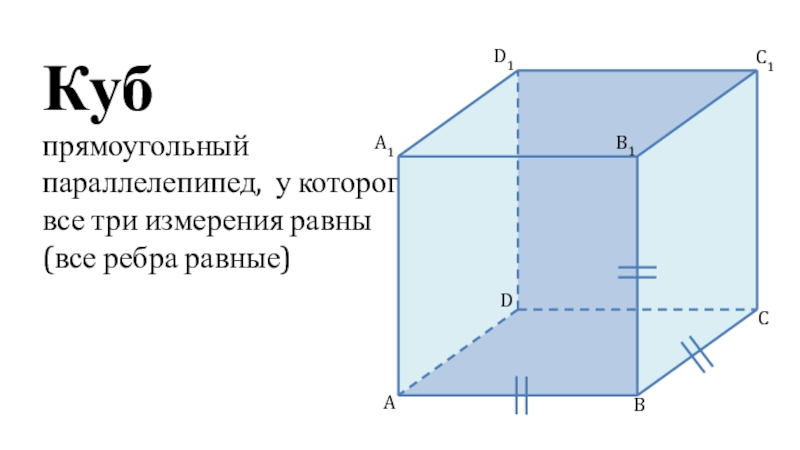
Боковые грани параллелепипеда являются прямоугольниками

⏊ DD1
Свойство №2
Все двухгранные углы прямоугольного параллелепипеда — прямые.
∠ADС —

∠ADD1С — также прямой.

измерений
Дано:
ABCDA1B1C1D1 — прямоугольный параллелепипед

Доказать:

 
Доказательство:
 
2) BB1 ⏊ DB, DB12 =

равные)

⇒ A1B2 = a2 + c2
3) C1C⏊ BC ⇒ △C1CB

20

19

11

a

b

c

d

Решение:

4) ABCD — прямоугольник ⇒ DB2 = a2 + b2

5)

Задача 1

Ответ: 21 см

параллелепипеда)

⏊ ( АА1D1D) ⇒ АD1 — проекция ВD1 ⇒ ∠AD1В

Решение:

Задача 2

12

ABCDA1B1C1D1 — прямоугольный параллелепипед

6

6

6

A

B

D1

12

D