Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Расчетно-графическая работа по дисциплине Теория принятия решений
Содержание
- 1. Расчетно-графическая работа по дисциплине Теория принятия решений
- 2. Задание На n участках могут выращиваться n культур.
- 3. 1 Построение математической моделиXiJ- структура посева i-й
- 4. 1 Построение математической модели1. Целевая функция:Суммарные затраты
- 5. 2 Расчетная частьСтруктура посева будет иметь следующий
- 6. 2 Расчетная частьДалее решаем методом искусственного базиса:Исходная симплекс-таблица:Конечная симплекс-таблица метода искусственного базиса:
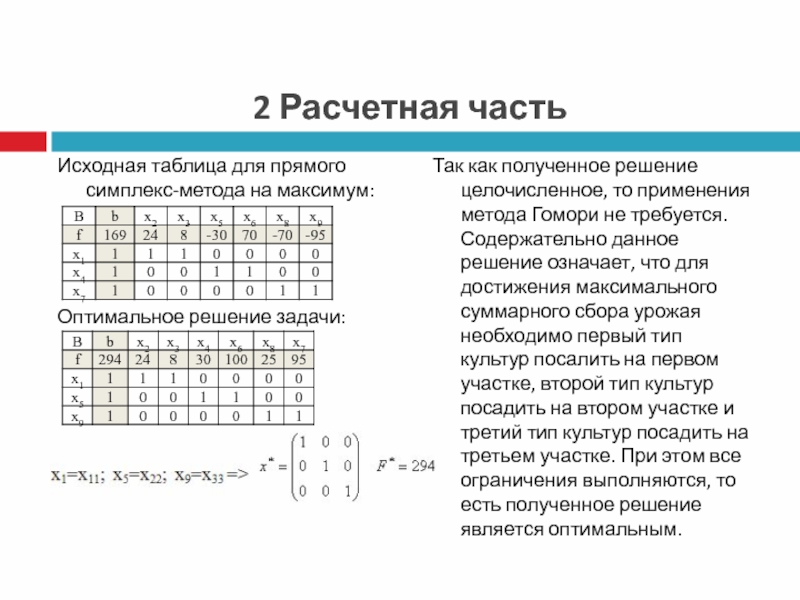
- 7. 2 Расчетная частьИсходная таблица для прямого симплекс-метода
- 8. ЗаключениеЗадачи математического программирования применяются в различных областях
- 9. Скачать презентанцию
Задание На n участках могут выращиваться n культур. Известны размеры участков в гектарах Bi, урожайность λik (ц/га) на каждом из участков по каждой культуре; Cik - затраты в чел/ч на 1 ц.;
Слайды и текст этой презентации
Слайд 1РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА ПО ДИСЦИПЛИНЕ
"ТЕОРИЯ ПРИНЯТИЯ РЕШЕНИЙ"
Выполнил: студент гр. ИВТ
– 315 Антосюк Е.В.
А.В.
Слайд 2Задание
На n участках могут выращиваться n культур. Известны размеры участков
в гектарах Bi, урожайность λik (ц/га) на каждом из участков
по каждой культуре; Cik - затраты в чел/ч на 1 ц.; PJ - плановое задание по сбору культур. 1. Определить структуру посевов, минимизирующую суммарные затраты;
2. Составить оптимальную структуру посевов, максимизирующую суммарный сбор урожая;
3. Решить задачу при плановом ассортиментном соотношении обеспечивая выполнения планового задания с минимальными затратами.
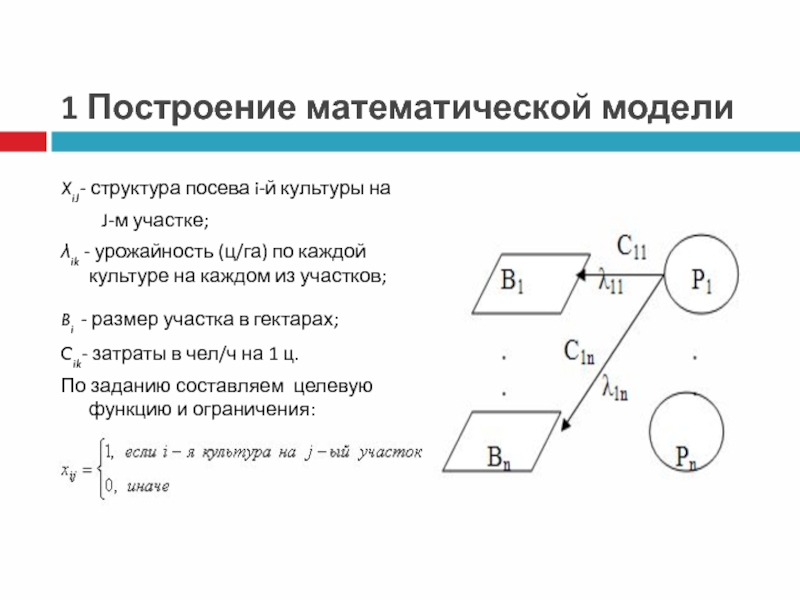
Слайд 31 Построение математической модели
XiJ- структура посева i-й культуры на
J-м
участке;
λik - урожайность (ц/га) по каждой культуре на каждом
из участков;Bi - размер участка в гектарах;
Cik- затраты в чел/ч на 1 ц.
По заданию составляем целевую функцию и ограничения:
Слайд 41 Построение математической модели
1. Целевая функция:
Суммарные затраты на посев минимизируем.
Ограничения:
2.
Целевая функция:
Оптимальная структура посевов, максимизирующая суммарный сбор урожая.
Ограничения:
3. Целевая функция:
Плановое
задание с минимальными затратамиОграничения:
Полученная задача является задачей целочисленного программирования.
Слайд 52 Расчетная часть
Структура посева будет иметь следующий вид:
Введём обозначения:
x11=x1; x12=x2;
x13=x3; x21=x4; x22=x5; x23=x6; x31=x7; x32=x8; x33=x9.
Зададим произвольные параметры урожайности
(ц/га) по каждой культуре на каждом из участков и размера участка в гектарах.Составим матрицу урожайности с числовыми значениями:
Также составим матрицу размера участка:
В результате получим следующую целевую функцию и ограничения:
L=64x1+40х2+56х3+100х4+130х5+30х6+
+5х7+75х8+100х9 → max
x1+x2+x3=1;
x4+x5+x6=1;
x7+x8+x9=1.
Слайд 62 Расчетная часть
Далее решаем методом искусственного базиса:
Исходная симплекс-таблица:
Конечная симплекс-таблица метода
искусственного базиса:
Слайд 72 Расчетная часть
Исходная таблица для прямого симплекс-метода на максимум:
Оптимальное решение
задачи:
Так как полученное решение целочисленное, то применения метода Гомори не
требуется. Содержательно данное решение означает, что для достижения максимального суммарного сбора урожая необходимо первый тип культур посалить на первом участке, второй тип культур посадить на втором участке и третий тип культур посадить на третьем участке. При этом все ограничения выполняются, то есть полученное решение является оптимальным.
Слайд 8Заключение
Задачи математического программирования применяются в различных областях человеческой деятельности в
целях оптимизации различных процессов и решения разнообразных задач. Поиск оптимальных
решений в них осуществляется с помощью специальных математических методов. В данной расчётно-графической работе по заданному условию задачи была составлена математическая модель и произведён расчёт задачи на примерных данных с помощью симплекс-метода, целью оптимизации в данном случае была максимизация суммарного сбора урожая.
