РАЗВЕРТКИ ПОВЕРХНОСТЕЙ

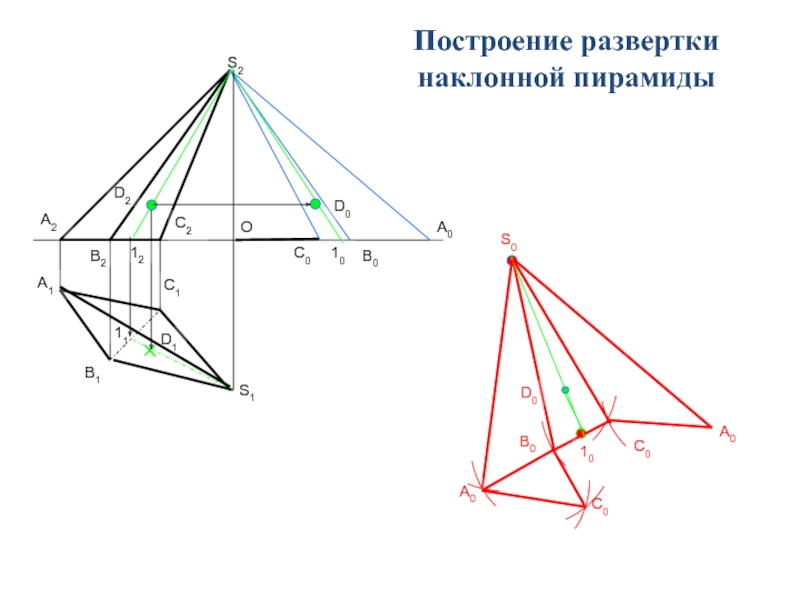
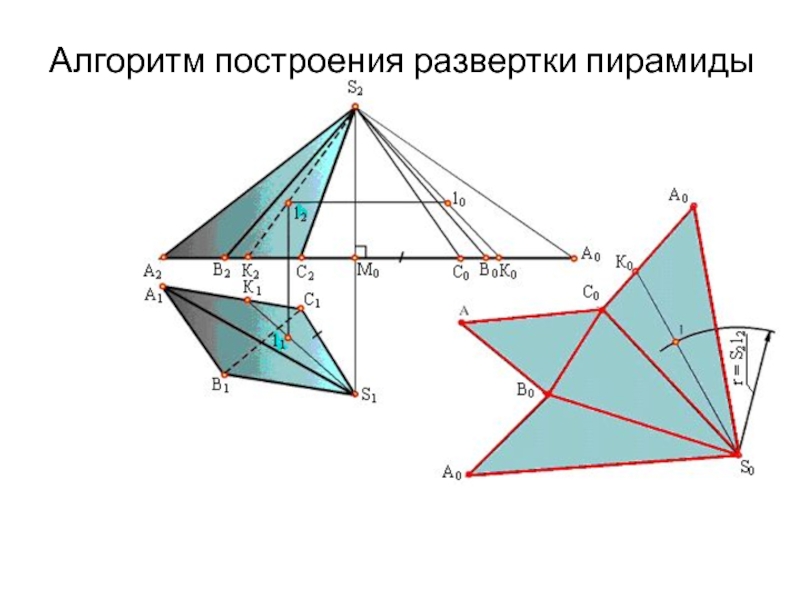
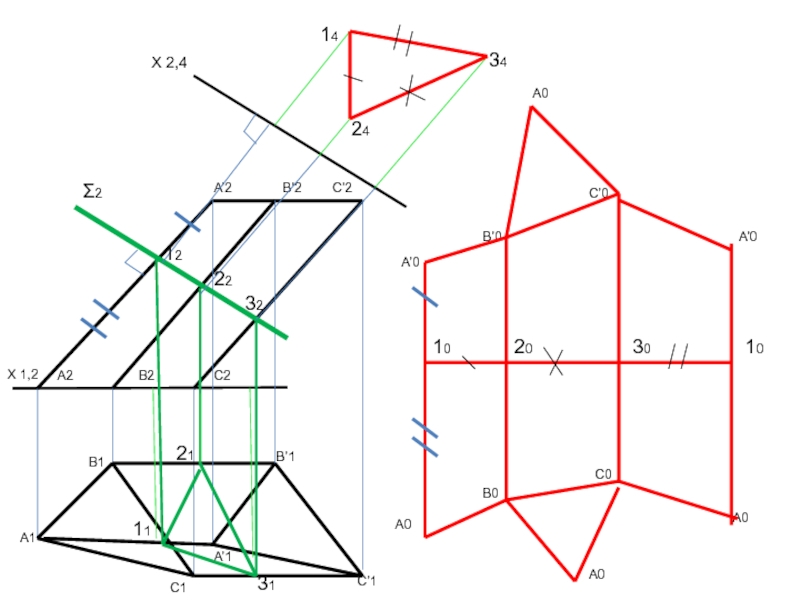
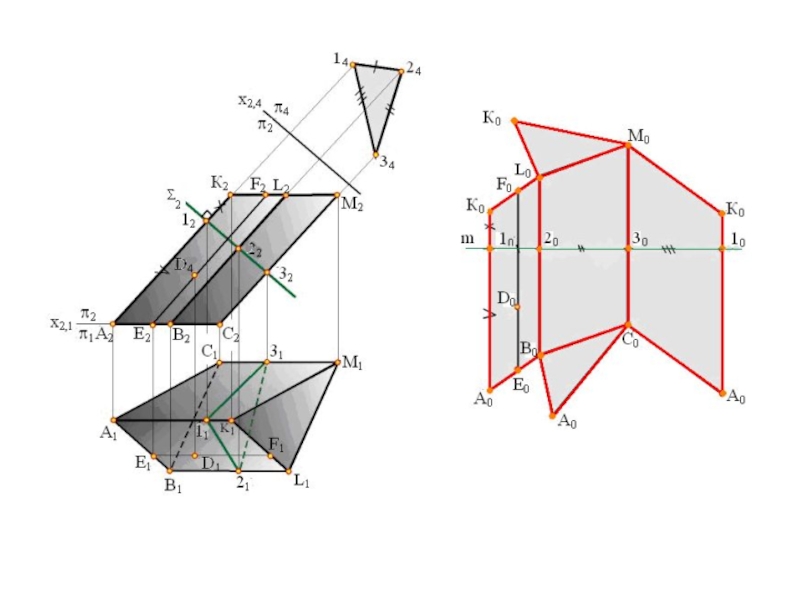
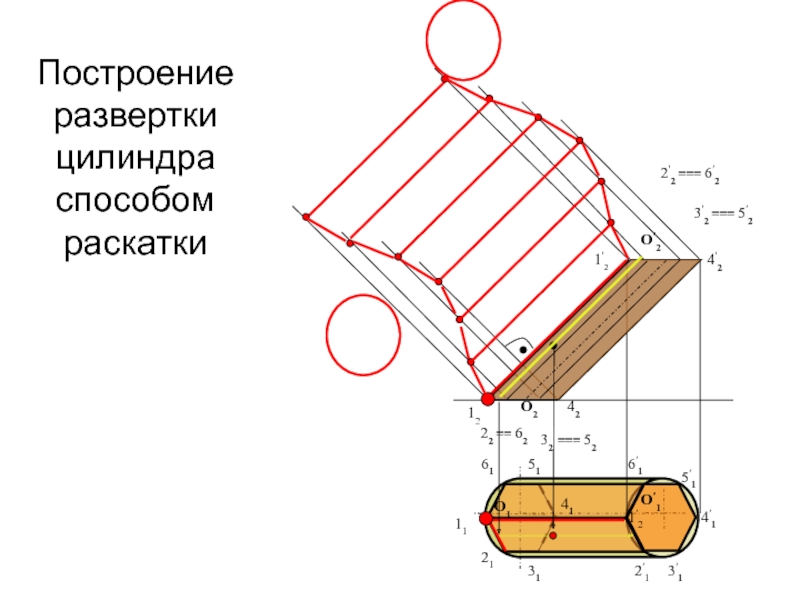
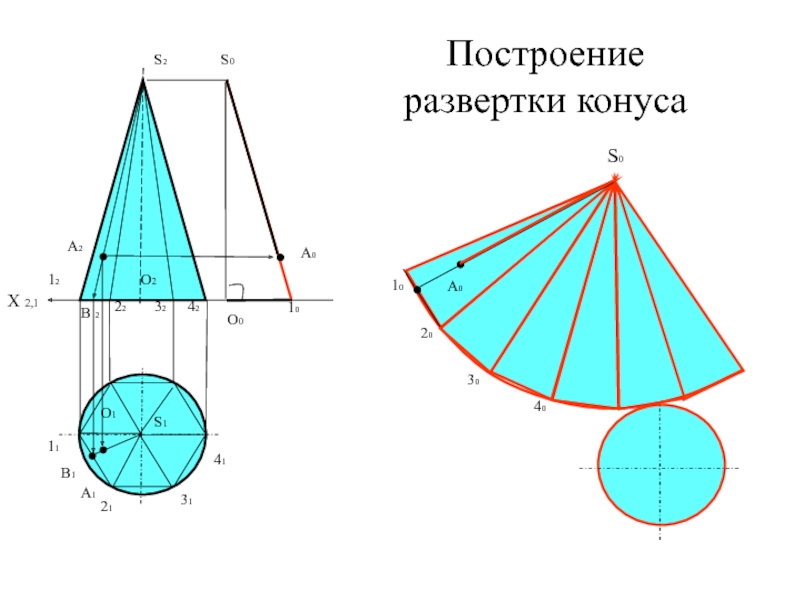
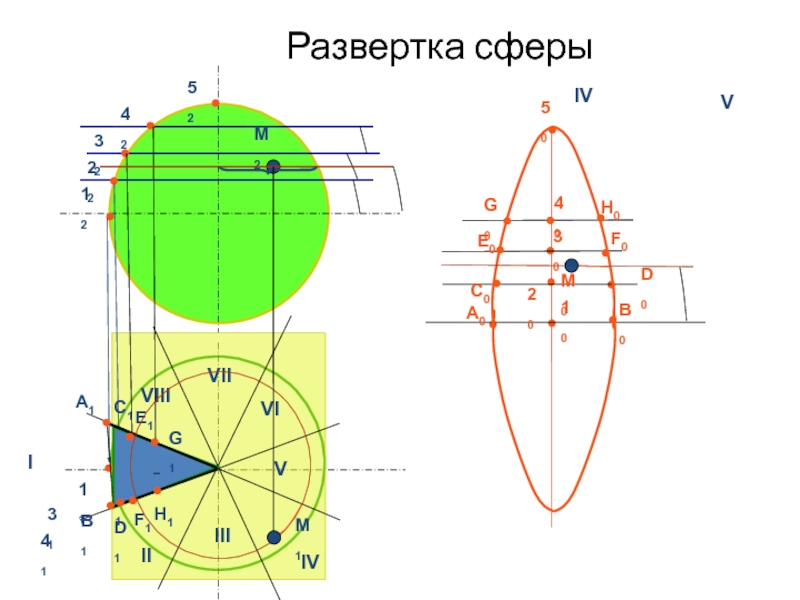
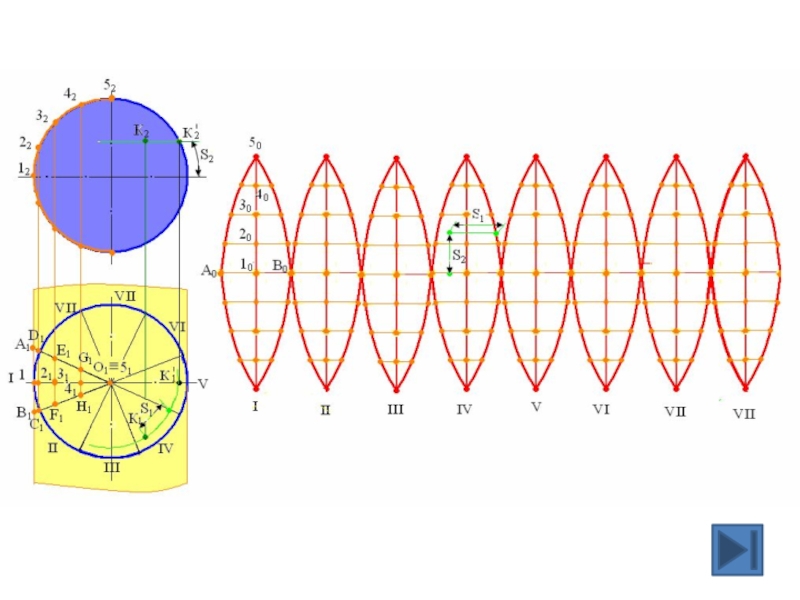
геометрического тела с одной плоскостью (без наложения граней или иных

элементов поверхности друг на друга).
Приступая к изучению развертки поверхности, последнюю целесообразно рассматривать как гибкую, нерастяжимую пленку. Некоторые из представленных таким образом поверхностей можно путем изгибания совместить с плоскостью. При этом, если отсек поверхности может быть совмещен с плоскостью без разрывов и склеивания, то такую поверхность называют развертывающейся.
Основные свойства развертки:
длины двух соответствующих линий поверхности и ее развертки равны между собой;
угол между линиями на поверхности равен углу между соответствующими им линиями на развертке;
прямой на поверхности соответствует также прямая на развертке;
параллельным прямым на поверхности соответствуют также параллельные прямые на развертке;
если линии, принадлежащей поверхности и соединяющей две точки поверхности, соответствует прямая на развертке, то эта линия является геодезической.

последовательным совмещением всех граней поверхности с плоскостью.
а) Пирамида и

ее развертка. Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины отдельных граней поверхности – плоских многоугольников.
Существует три метода построения развертки многогранных поверхностей:
1. Метод треугольника.
2. Метод нормального сечения.
3. Метод раскатки.
Рассмотрим применение каждого метода на примерах развертки пирамиды (метод треугольника) и призмы (метод нормального сечения и раскатки)

Пересечение призмы проецирующей плоскостью

цилиндра способом раскатки